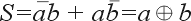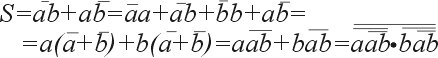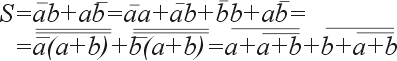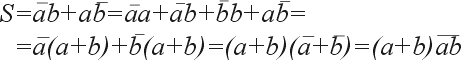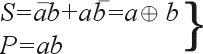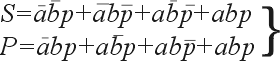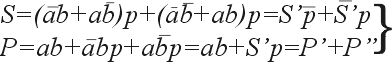для чего нужен сумматор
Принцип работы сумматора
Сумматоры. Устройство, принцип работы
Сумматоры — это комбинационные устройства, предназначенные для сложения чисел.
Функционирование однозарядного сумматора показано в таблице, приведённой на рис.10.30. В этом случае при сложении слагаемых используется перевод десятичных чисел в двоичные числа.
Pиc.10.29. Символическое изображение одноразрядного двоичного сумматора
При сложении слагаемых или 0+1+0 получается десятичное число 1. Такому числу соответствует двоичное число 01, при этом Аналогично, 1+1+0 = 2, которому соответствует двоичное число 10, при этом . При сложении чисел 1+1+1 = 3, которому соответствует двоичное число 11, при этом и так далее.
Сумматоры могут быть последовательного и параллельного действия. В сумматорах последовательного действия коды двоичных чисел вводятся в последовательной форме слагаемое за слагаемым, начиная с младшего разряда.
На рис.10.31 изображена схема сумматора последовательного действия, предназначенного для суммирования четырёхразрядных двоичных чисел. Сумматор построен на трёх регистрах сдвига, D-триггере и на одноразрядном сумматоре.
Рис.10.30. Таблица функционирования одноразрядного сумматора
Рис.10.31. Схема сумматора последовательного действия
Функционирование сумматора приведено в таблице рис.10.32, где слагаемое pi для первого разряда всегда равно нулю.
Рис.10.32. Таблица функционирования сумматора
Для ускорения операции сложения используются сумматоры параллельного действия, которые состоят из нескольких однозарядных сумматоров. В таких сумматорах слагаемые поступают одновременно на соответствующие входы однозарядных сумматоров, при этом каждый из однозарядных сумматоров формирует на своих выходах суммы соответствующих разрядов и слагаемые переноса, передаваемых на входы старших разрядов. Схема четырёхразрядного сумматора параллельного действия приведена на рис.10.33.
Рис.10.33. Схема четырёхразрядного сумматора параллельного действия
Что такое сумматор
В общем смысле слова, сумматор – это какое-либо устройство, которое что-либо суммирует и выдает на выходе сумму этих воздействий. Сумматор можно представить в виде какого-либо неизвестного нам ящика, на который поступает входные воздействия и на выходе такого ящика выдается их сумма.
В электронике сумматоры делятся на две группы:
В этой статье мы будем разбирать аналоговые сумматоры.
Аналоговый сумматор
Многие помнят осциллограмму постоянного напряжения.
Если, допустим, цена нашего квадратика 1 В, то на данной картинке мы видим постоянное напряжение амплитудой в 1 В. Суммировать постоянное напряжение – одно удовольствие. Для этого достаточно сложить амплитуды этих сигналов в любой момент времени.
На рисунке ниже мы видим два сигнала A и B и сумму этих сигналов: A+B. Если сигнал A = 2 В, сигнал B = 1 В, то сумма этих сигналов составит 3 В.
Все то же самое касается и сигналов с отрицательной полярностью.
При сложении сигналов с равной амплитудой, но разной полярности, в сумме получаем 0. То есть эти два сигнала взаимно себя скомпенсировали: 1 +(-1)=0. Все становится намного веселее, если мы начинаем складывать сигналы, которые меняются во времени, то есть переменные сигналы. Они могут быть как периодические, так и непериодические.
Рассмотрим самый простой пример. Есть два синусоидальных сигнала с одинаковыми амплитудами, частотами и фазами. Подадим их на сумматор. Что получится в итоге?
В момент времени t1 у нас амплитуда сигнала А была равна 1 В, амплитуда сигнала В тоже 1 В.
В сумме их результат в момент времени t1 будет равен 2 В, что мы и видим на сигнале A+B
Если сместить фазу одного из сигналов на 180 градусов, относительно другого, а амплитуды и частоты сигналов оставить без изменения, то чему будет равняться их сумма? Сместим второй сигнал на 180 градусов и суммируем их амплитуды в каждый момент времени. Сумма будет равняться нулю, что и видно на рисунке ниже.
Сложение двух сигналов в Proteus
Если надо сложить в теории два каких-нибудь два сложных сигнала с разными фазами, амплитудами, частотами, то проще всего прибегнуть к различным симуляторам.
Один из них – это Proteus. С помощью него можно сложить два любых сигнала и посмотреть их сумму.
Для этого надо выбрать синусоидальный генератор.
Затем виртуальный осциллограф.
Задать параметры генератору.
Теперь можно сложить два синусоидальных сигнала с одинаковыми амплитудами, фазами и частотами.
Прописать амплитуду и частоту каждого сигнала и нажать «пуск».
Нажать правой кнопкой мыши на виртуальный осциллограф и нажать Digital Oscilloscope.
Для того, чтобы найти их сумму, достаточно нажать на кнопку A+B.
Получаем сумму двух сигналов.
В таком виртуальном осциллографе можно складывать любые два сигнала.
Сумматоры и цифровые компараторы: принцип работы, схемы
 Что такое сумматоры?
Что такое сумматоры?
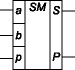
Сумматоры — это комбинационные устройства, предназначенные для сложения чисел. Рассмотрим сложение двух одноразрядных двоичных чисел, для чего составим таблицу сложения (таблицу истинности), в которой отразим значения входных чисел А и В, значение результата суммирования S и значение переноса в старший разряд P (см. рис. 3.48).
Цифровые сумматоры
Работа устройства, реализующего таблицу истинность (рис. 3.48), описывается следующими уравнениями
Очевидно, что по отношении: к столбцу S реализуется логическая функция «исключающее ИЛИ», т. е. S = А + В.
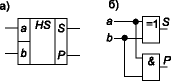
Поскольку полусумматор имеет только два входа, он может использоваться для суммирования лишь в младшем разряде.
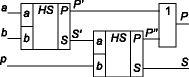
При суммировании двух многоразрядных чисел для каждого разряда (кроме младшего) необходимо использовать устройство, имеющее дополнительный вход переноса. Такое устройство (рис. 3.50) называют полным сумматором и его можно представить как объединение двух полусумматоров (Рвх — дополнительный вход переноса).
Цифровые компараторы
Цифровые компараторы выполняют сравнение двух чисел, заданных в двоичном коде. Они могут определять равенство двух двоичных чисел A и B с одинаковым количеством разрядов либо вид неравенства A> B или A Задать вопрос
Из анализа схемы следует, что если A= B, то F = 1, в противном случае, т. е. при А ≠ В, F = 0. Если А > В, т. е. А = 1, В = 0, то С = 1, а если А В обеспечивается (для четырехразрядного числа) в четырех случаях: или А4 > В4, или А4 = В4 и А3 > В3, или А4 = В4, А3 = В3 и А2 > В2, или А4 = В4, А3 = В3, А2 = В2 и A1 > В1 (где А4 и В4 — старшие разряды чисел А и В). Очевидно, что если поменять местами А1 и B1, то будет выполняться неравенство А В, что позволяет наращивать разрядность обоих чисел. Для этого компараторы соединяют каскадно или параллельно (пирамидально).
Сумматоры: определения, классификация, уравнения, структуры и применение
Основной элементарной операцией, выполняемой над кодами чисел в цифровых устройствах, является арифметическое сложение.
Сумматор — логический операционный узел, выполняющий арифметическое сложение кодов двух чисел. При арифметическом сложении выполняются и другие дополнительные операции: учёт знаков чисел, выравнивание порядков слагаемых и тому подобное. Указанные операции выполняются в арифметическо-логических устройствах (АЛУ) или процессорных элементах, ядром которых являются сумматоры.
Сумматоры классифицируют по различным признакам.
Параллельный сумматор в простейшем случае представляет собой n одноразрядных сумматоров, последовательно (от младших разрядов к старшим) соединённых цепями переноса. Однако такая схема сумматора характеризуется сравнительно невысоким быстродействием, так как формирование сигналов суммы и переноса в каждом i-ом разряде производится лишь после того, как поступит сигнал переноса с (i-1)-го разряда.Таким образом, быстродействие сумматора определяется временем распространения сигнала по цепи переноса. Уменьшение этого времени — основная задача при построении параллельных сумматоров.
Для уменьшения времени распространения сигнала переноса применяют: конструктивные решения, когда используют в цепи переноса наиболее быстродействующие элементы; тщательно выполняют монтаж без длинных проводников и паразитных ёмкостных составляющих нагрузки и (наиболее часто) структурные методы ускорения прохождения сигнала переноса.
Сумматоры, которые имеют постоянное время, отводимое для суммирования, независимое от значений слагаемых, называют синхронными.
Последние две структуры строятся либо на счётных триггерах (сейчас практически не используются), либо по структуре “комбинационный сумматор – регистр хранения” (сейчас наиболее употребляемая схема).
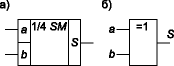
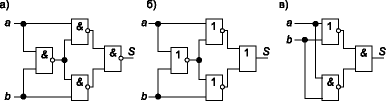
Простейшим двоичным суммирующим элементом является четвертьсумматор. Происхождение названия этого элемента следует из того, что он имеет в два раза меньше выходов и в два раза меньше строк в таблице истинности по сравнению с полным двоичным одноразрядным сумматором. Наиболее известны для данной схемы названия: элемент “сумма по модулю 2” и элемент “исключающее ИЛИ”. Схема (рис. 1) имеет два входа а и b для двух слагаемых и один выход S для суммы. Работу её отражает таблица истинности 1 (табл. 1), а соответствующее уравнение имеет вид
 Что такое сумматоры?
Что такое сумматоры?