для чего нужен тангенс
Тангенс угла это отношение чего? Основы тригонометрии
Определение

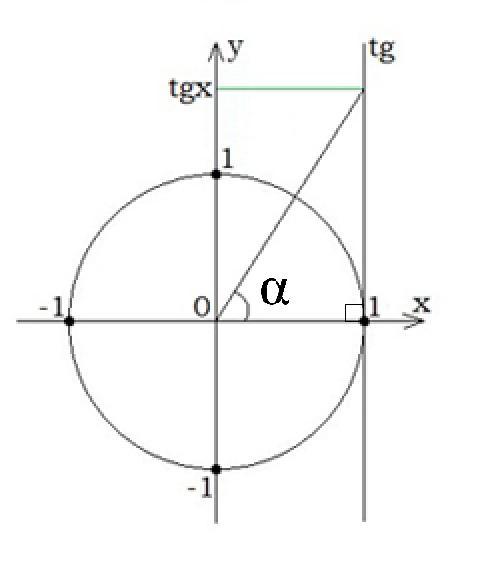
Теперь перейдем к определению тангенса, которое несет алгебраический смысл, для этого нам понадобится единичная окружность.
Для того чтобы отметить в декартовой системе координат численное значение тангенса необходимо для начала провести прямую х = 1, которая будет перпендикулярна оси абсцисс и параллельна оси ординат. После чего отложим от оси абсцисс угол альфа и продлим его сторону до пересечения с прямой х = 1. Ордината точки пересечения в конкретной ситуации будет являться численным значением тангенса отложенного угла.
Как связаны тангенс с котангенсом?
Тангенс является обратной функцией от котангенса, а это значит что: tg = 1/ctg. Таким образом, отношение тангенса к котангенсу является равным единице: tg/ctg = 1.
Существует ли связь тангенса с косинусом?
Существует такое тождество, определяющее связь этих двух тригонометрических функций: 1 + tg2 = 1/cos2. Попробуем доказать это тождество, преобразуя его левую часть с помощью алгебраического определения тангенса:
Теперь приведем выражение к общему знаменателю:
Вспомним главное тригонометрическое тождество и упростим выражение, после чего получим:
Эта дробь является равной правой части данного изначально выражения, таким образом мы доказали тождество.
Заключение
Что такое синус и косинус? Что такое тангенс и котангенс?
Что такое тригонометрия
Но давайте начнем совсем с азов. Раз уж мы сказали, что СИНУС – это некая тригонометрическая функция, давайте расскажем и что такое тригонометрия.
Тригонометрия – это раздел математики, который был основан еще в Древней Греции. Само слово состоит из двух половин «τρίγωνον» и «μετρέω», что можно дословно перевести как «изучение треугольников».
Впервые нечто похожее на тригонометрические функции появилось в Древней Греции. Во всяком случае, их можно отследить по трудам Евклида и Архимеда, то есть в III веке до нашей эры.
Хотя ученые не исключают, что похожими вычислениями пользовались и при строительстве Египетских пирамид. А это уже 2-2,5 тысячи лет до нашей эры.
И опять же, пирамиды ведь имеют треугольную форму (в плоскости). И тригонометрия связана напрямую с треугольниками. Возможно совпадение, а возможно и нет.
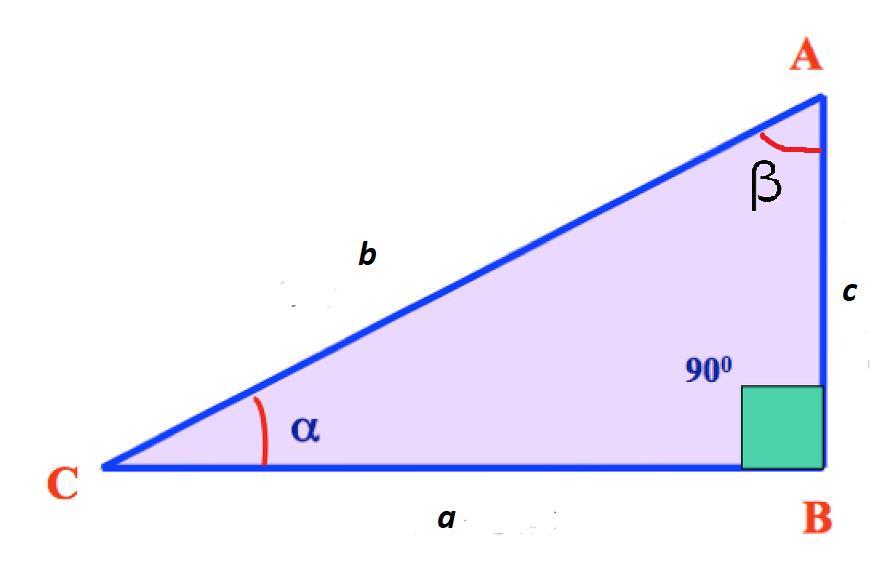
Правда, в тригонометрии рассматривают конкретные треугольники – прямоугольные. Напомним, это такие фигуры, у которых две стороны из трех пересекаются друг с другом под углом 90 градусов.
Выглядит такой треугольник вот так:
У такого треугольника стороны имеют определенные названия:
КАТЕТЫ – это стороны, которые пересекаются под прямым углом.
В нашем случае это стороны АВ и ВС. Это название также имеет древнегреческие корни. Так, слово «káthetos» переводится как «перпендикуляр, опущенный, ответственный».
ГИПОТЕНУЗА – сторона, которая идет под наклоном и соединяет между собой два катета.
В нашем случае это отрезок АС. Слово также родом из Древней Греции, «ὑποτείνουσα» означает «натянутая». И это очень хорошо характеризует этот отрезок, ведь он действительно выглядит как натянутая струна между двух опор. И даже если перевернуть треугольник, это ощущение не изменится.
Видео
Связь между тангенсом и котангенсом
Уж насколько очевидной кажется связь между ранее рассмотренными тождествами, настолько еще более наглядна связь между тангенсом и котангенсом одного угла.
Такое тождество применимо и справедливо при любых углах α, значение которых не равняются π/2 * z, где z — это любое целое число. В противном случае, функции не будут определены.
Как и любое другое, данное тригонометрическое тождество подлежит доказательству. Доказывать его очень просто.
tg α * ctg α = 1.
Получается, что тангенс и котангенс одного угла, при котором они имеют смысл — это взаимно обратные числа.
Если числа a и b взаимно обратные — это значит, что число a — это число, обратное числу b, а число b — это число, обратное числу a. Кроме того, это значит, что числу a обратно число b, а числу b обратно число a. Короче, и так, и эдак.
Взаимно обратные числа — это два числа, произведение которых равно 1.
Числа
Как быть с определением синуса, косинуса, тангенса и котангенса числа, а не угла поворота?
Синус, косинус, тангенс, котангенс числа
Синусом, косинусом, тангенсом и котангенсом числа t называется число, которое соответственно равно синусу, косинусу, тангенсу и котангенсу в t радиан.
Например, синус числа 10 π равен синусу угла поворота величиной 10 π рад.
Существует и другой подход к определению синуса, косинуса, тангенса и котангенса числа. Рассмотрим его подробнее.
Любому действительному числу t ставится в соответствие точка на единичной окружности с центром в начале прямоугольной декартовой системы координат. Синус, косинус, тангенс и котангенс определяются через координаты этой точки.
Теперь, когда связь числа и точки на окружности установлена, переходим к определению синуса, косинуса, тангенса и котангенса.
Синус числа t — ордината точки единичной окружности, соответствующей числу t. sin t=y
Косинус (cos) числа t
Косинус числа t — абсцисса точки единичной окружности, соответствующей числу t. cos t=x
Тангенс (tg) числа t
Тангенс числа t — отношение ординаты к абсциссе точки единичной окружности, соответствующей числу t. tg t=yx=sin tcos t
Последние определения находятся в соответствии и не противоречат определению, данному в начале это пункта. Точка на окружности, соответствующая числу t, совпадает с точкой, в которую переходит начальная точка после поворота на угол t радиан.
Примеры решения задач
Разберем пару задачек, для решения которых нужно знать основные тождества. Рассмотрите внимательно предложенные решения и потренируйтесь самостоятельно.
Задачка 1. Найдите cos α, tg α, ctg α при условии, что sin α = 12/13.
Задачка 2. Найдите значение cos α, если:
Как видите, задачи решаются достаточно просто, нужно лишь верно применять формулы основных тождеств.
Геометрия. Урок 1. Тригонометрия
Смотрите бесплатные видео-уроки по теме “Тригонометрия” на канале Ёжику Понятно.
Видео-уроки на канале Ёжику Понятно. Подпишись!
Содержание страницы:
Тригонометрия в прямоугольном треугольнике
Рассмотрим прямоугольный треугольник. Для каждого из острых углов найдем прилежащий к нему катет и противолежащий.
Синус угла – отношение противолежащего катета к гипотенузе.
sin α = Противолежащий катет гипотенуза
Косинус угла – отношение прилежащего катета к гипотенузе.
cos α = Прилежащий катет гипотенуза
Тангенс угла – отношение противолежащего катета к прилежащему (или отношение синуса к косинусу).
tg α = Противолежащий катет Прилежащий катет
Котангенс угла – отношение прилежащего катета к противолежащему (или отношение косинуса к синусу).
ctg α = Прилежащий катет Противолежащий катет
tg ∠ A = sin ∠ A cos ∠ A = C B A C
ctg ∠ A = cos ∠ A sin ∠ A = A C C B
tg ∠ B = sin ∠ B cos ∠ B = A C C B
ctg ∠ B = cos ∠ B sin ∠ B = C B A C
Тригонометрия: Тригонометрический круг
Тригонометрия на окружности – это довольно интересная абстракция в математике. Если понять основной концепт так называемого “тригонометрического круга”, то вся тригонометрия будет вам подвластна. В описании к видео есть динамическая модель тригонометрического круга.
Тригонометрический круг – это окружность единичного радиуса с центром в начале координат.
Рассмотрим прямоугольный треугольник A O B :
cos α = O B O A = O B 1 = O B
sin α = A B O A = A B 1 = A B
Итак, косинус угла – координата точки A по оси x (ось абсцисс), синус угла – координата точки A по оси y (ось ординат).
Давайте рассмотрим еще один случай, когда угол α – тупой, то есть больше 90 ° :
Ещё одно замечание.
Синус тупого угла – положительная величина, а косинус – отрицательная.
Основное тригонометрическое тождество
sin 2 α + cos 2 α = 1
Данное тождество – теорема Пифагора в прямоугольном треугольнике O A B :
A B 2 + O B 2 = O A 2
sin 2 α + cos 2 α = R 2
sin 2 α + cos 2 α = 1
Тригонометрия: Таблица значений тригонометрических функций
Тригонометрия: градусы и радианы
Как перевести градусы в радианы, а радианы в градусы? Как и когда возникла градусная мера угла? Что такое радианы и радианная мера угла? Ищите ответы в этом видео!
Тригонометрия: Формулы приведения
Тригонометрия на окружности имеет некоторые закономерности. Если внимательно рассмотреть данный рисунок,
можно заметить, что:
sin 180 ° = sin ( 180 ° − 0 ° ) = sin 0 °
sin 150 ° = sin ( 180 ° − 30 ° ) = sin 30 °
sin 135 ° = sin ( 180 ° − 45 ° ) = sin 45 °
sin 120 ° = sin ( 180 ° − 60 ° ) = sin 60 °
cos 180 ° = cos ( 180 ° − 0 ° ) = − cos 0 °
cos 150 ° = cos ( 180 ° − 30 ° ) = − cos 30 °
cos 135 ° = cos ( 180 ° − 45 ° ) = − cos 45 °
cos 120 ° = cos ( 180 ° − 60 ° ) = − cos 60 °
Рассмотрим тупой угол β :
Для произвольного тупого угла β = 180 ° − α всегда будут справедливы следующие равенства:
sin ( 180 ° − α ) = sin α
cos ( 180 ° − α ) = − cos α
tg ( 180 ° − α ) = − tg α
ctg ( 180 ° − α ) = − ctg α
Тригонометрия: Теорема синусов
В произвольном треугольнике стороны пропорциональны синусам противолежащих углов.
a sin ∠ A = b sin ∠ B = c sin ∠ C
Тригонометрия: Расширенная теорема синусов
Отношение стороны к синусу противолежащего угла равно двум радиусам описанной вокруг данного треугольника окружности.
a sin ∠ A = b sin ∠ B = c sin ∠ C = 2 R
Тригонометрия: Теорема косинусов
Квадрат стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними.
a 2 = b 2 + c 2 − 2 b c ⋅ cos ∠ A
b 2 = a 2 + c 2 − 2 a c ⋅ cos ∠ B
c 2 = a 2 + b 2 − 2 a b ⋅ cos ∠ C
Примеры решений заданий из ОГЭ
Модуль геометрия: задания, связанные с тригонометрией.
Тригонометрия: Тригонометрические уравнения
Это тема 10-11 классов.
Из серии видео ниже вы узнаете, как решать простейшие тригонометрические уравнения, что такое обратные тригонометрические функции, зачем они нужны и как их использовать. Если вы поймёте эти базовые темы, то вскоре сможете без проблем решать любые тригонометрические уравнения любого уровня сложности!
Синус, косинус, тангенс и котангенс: определения в тригонометрии, примеры, формулы
Данная статья посвящена базовым понятиям и дефинициям тригонометрии. В ней рассмотрены определения основных тригонометрических функций: синуса, косинуса, тангенса и котангенса. Разъяснен и проиллюстрирован их смысл в контексте геометрии.
Синус, косинус, тангенс и котангенс. Определения
Изначально определения тригонометрических функций, аргументом которых является угол, выражались через соотношения сторон прямоугольного треугольника.
Определения тригонометрических функций
Данные определения даны для острого угла прямоугольного треугольника!
В треугольнике ABC с прямым углом С синус угла А равен отношению катета BC к гипотенузе AB.
Определения синуса, косинуса, тангенса и котангенса позволяют вычислять значения этих функций по известным длинам сторон треугольника.
Угол поворота
В данном контексте можно дать определение синуса, косинуса, тангенса и котангенса угла произвольной величины. Представим единичную окружность с центром в начале декартовой системы координат.
Синус (sin) угла поворота
При решении практических примеров не говорят «синус угла поворота α «. Слова «угол поворота» просто опускают, подразумевая, что из контекста и так понятно, о чем идет речь.
Числа
Как быть с определением синуса, косинуса, тангенса и котангенса числа, а не угла поворота?
Синус, косинус, тангенс, котангенс числа
Синусом, косинусом, тангенсом и котангенсом числа t называется число, которое соответственно равно синусу, косинусу, тангенсу и котангенсу в t радиан.
Например, синус числа 10 π равен синусу угла поворота величиной 10 π рад.
Существует и другой подход к определению синуса, косинуса, тангенса и котангенса числа. Рассмотрим его подробнее.
Любому действительному числу t ставится в соответствие точка на единичной окружности с центром в начале прямоугольной декартовой системы координат. Синус, косинус, тангенс и котангенс определяются через координаты этой точки.
Теперь, когда связь числа и точки на окружности установлена, переходим к определению синуса, косинуса, тангенса и котангенса.
Последние определения находятся в соответствии и не противоречат определению, данному в начале это пункта. Точка на окружности, соответствующая числу t, совпадает с точкой, в которую переходит начальная точка после поворота на угол t радиан.
Тригонометрические функции углового и числового аргумента
Основные функции тригонометрии
Из контекста обычно понятно, с каким аргументом тригонометрической функции (угловой аргумент или числовой аргумент) мы имеем дело.
Связь определений sin, cos, tg и ctg из геометрии и тригонометрии
Вернемся к данным в самом начале определениям и углу альфа, лежащему в пределах от 0 до 90 градусов. Тригонометрические определения синуса, косинуса, тангенса и котангенса полностью согласуются с геометрическими определениями, данными с помощью соотношений сторон прямоугольного треугольника. Покажем это.
В соответствии с определением из геометрии, синус угла α равен отношению противолежащего катета к гипотенузе.
sin α = A 1 H O A 1 = y 1 = y
Аналогично соответствие определений можно показать для косинуса, тангенса и котангенса.
Зачем нужны тангенсы?
11 Mar 2021 в 11:30
11 Mar 2021 в 11:56 #26
Абориген, ты 8 классов закончил хоть?
у этого бурята нету школ в степях
11 Mar 2021 в 11:59 #27
Кто-нибуть может обьяснить зачем нам в жизни синусы, косинусы, тангенсы и т.д?
Мне 1 чел рассказывал, что использовал арктангенс для просчитывания траектории снежинок на своем сайте.Но я так и не понял в чём прикол, оно ж не волной летит, рандомно, куда ветер подует.
Это все названия отношений одних длин к другим.
Вот и математики вывели себе ряд отношений между сторонами, с которыми им удобнее работать.
11 Mar 2021 в 12:01 #28
я архитектор и мы такое не используем kekw
ландшафтным дизайнерам наверное и не нужно это.
11 Mar 2021 в 12:03 #29
ландшафтным дизайнерам наверное и не нужно это.
Нет, я именно архитектор. Проектирую дома и прочее
11 Mar 2021 в 12:05 #30
Вот и математики вывели себе ряд отношений между сторонами, с которыми им удобнее работать.
Так я понимаю что это отношение.Вопрос в том, ЗАЧЕМ делить одну сторону на другую? что это показывает? попробуй придумать простой пример с кошечками и собачками если понимаешь о чём говоришь
11 Mar 2021 в 12:11 #31
Кто-нибуть может обьяснить зачем нам в жизни синусы, косинусы, тангенсы и т.д?
Мне 1 чел рассказывал, что использовал арктангенс для просчитывания траектории снежинок на своем сайте.Но я так и не понял в чём прикол, оно ж не волной летит, рандомно, куда ветер подует.
«Проектировал» себе лестницу для дома. Пригодились для вычисления длины/угла лестницы.
Вообще, геометрия в ремонте не редко выручает.
11 Mar 2021 в 12:19 #32
11 Mar 2021 в 12:20 #33
Кто-нибуть может обьяснить зачем нам в жизни синусы, косинусы, тангенсы и т.д?
Мне 1 чел рассказывал, что использовал арктангенс для просчитывания траектории снежинок на своем сайте.Но я так и не понял в чём прикол, оно ж не волной летит, рандомно, куда ветер подует.
что такое тангенс вообще?
я просто тимлид архитектор синьор питон датасаинс програмист с зп 9999999 баксов в секунду, я такого не знаю
11 Mar 2021 в 12:22 #34
Так я понимаю что это отношение.Вопрос в том, ЗАЧЕМ делить одну сторону на другую? что это показывает? попробуй придумать простой пример с кошечками и собачками если понимаешь о чём говоришь
Чтобы знать как их размеры взаимосвязаны.
Возьмём другой пример.
Ты издалека видишь его «маленьким».
На пример со своим же пальцем.
Грубо говоря смотришь в сторону столба, подносишь кулак с большим пальцем и сравниваешь и узнаешь расстояние.
Так и с тангенсом. Ты вроде сравниваешь высоту пальца с высотой объекта, но на деле узнаешь расстояние до.
11 Mar 2021 в 12:22 #35
Движение рыб в воде происходит по закону синуса или косинуса, если зафиксировать точку на хвосте, а потом рассмотреть траекторию движения. При плавании тело рыбы принимает форму
11 Mar 2021 в 12:24 #36
11 Mar 2021 в 12:34 #37
Кто-нибуть может обьяснить зачем нам в жизни синусы, косинусы, тангенсы и т.д?
Мне 1 чел рассказывал, что использовал арктангенс для просчитывания траектории снежинок на своем сайте.Но я так и не понял в чём прикол, оно ж не волной летит, рандомно, куда ветер подует.
Для того, чтобы все 18 (или сколько их там) полигонов морфа красиво визуализировать. В компьютерной графике короче, ну и AR/VR всяких там. В физике ещё, очевидно. В школе решают задачу, при каком угле наклона брусок скатится с наклонной плоскости. Так вот, ответ, что угол равен арктангенсу коэф. трения.
11 Mar 2021 в 12:44 #38
какой-то абсурдный вопрос
это же математика, движок вселенной
вот зачем нам число 783842? вот з а ч е м?
а вот эти цифры зачем нам 4 8 15 16 23 42?
11 Mar 2021 в 12:47 #39
арктангенсу коэф. трения.
прикол. Да эта тема сама по себе интересна. Более того полезна для развития аналитич мышления
11 Mar 2021 в 12:51 #40
Глубокая нейронная сеть на сигмоиде в теории является универсальным аппроксиматором. Хочешь сказать нейросети не нужны?
11 Mar 2021 в 12:55 #41
Не знаю, что там с тангусами, но про практическое применение математики в жизни есть интересный мини-сериал документальный, называется
«Числа. Пять чисел, которые изменили мир». Рекомендую. В Ютубе есть
11 Mar 2021 в 12:56 #42
Синапсы лишними не бывают, учись солдат.
11 Mar 2021 в 13:00 #43
Кто-нибуть может обьяснить зачем нам в жизни синусы, косинусы, тангенсы и т.д?
Мне 1 чел рассказывал, что использовал арктангенс для просчитывания траектории снежинок на своем сайте.Но я так и не понял в чём прикол, оно ж не волной летит, рандомно, куда ветер подует.
Как тут уже говорили, для программирования в геймдеве. Например, у тебя есть объект, известна скорость «v» и угол «a» направления движения. Игра должна на каждом шаге вычислять приращения координат:
И подобных примеров масса, особенно в 3D-графике. Если займешься программированием игр, то столкнешься с необходимостью решать такие задачи.
11 Mar 2021 в 13:01 #44
Кто-нибуть может обьяснить зачем нам в жизни синусы, косинусы, тангенсы и т.д?
Мне 1 чел рассказывал, что использовал арктангенс для просчитывания траектории снежинок на своем сайте.Но я так и не понял в чём прикол, оно ж не волной летит, рандомно, куда ветер подует.
тангенсом угла называется отношение
отношение противолежащего катета к прилежащему
Ничего невероятного в этом нет. Более того это имеет прикладное применение)))
PS. OAB это треугольник
Катет это сторона. Гипотенуза всегда больше любого и катетов))
Тангес относится к тригонометрических функций по простому к элементарным, очевидным. Это все придумали еще за 100 лет до нашей эры, то есть 2100 лет назад))
11 Mar 2021 в 13:04 #45
какой-то абсурдный вопрос
это же математика, движок вселенной
вот зачем нам число 783842? вот з а ч е м?
Что б определить темно красный цвет
11 Mar 2021 в 13:08 #46
зачем нам в жизни синусы, косинусы, тангенсы и т.д?
первая же ссылка в гугле
11 Mar 2021 в 13:15 #47
Большинство этих вычислений делается с помощью прикладных приложений.
Например, челик в интернете выпендривался, что ему пригодился тангенс для вычисления постройки лестницы в своём доме (справедливо), но в то же время продвинутый чел прикинет всё это за 2 минуты, просто нарисовав в автокаде без конкретных знаний тригонометрии.
Подобные знания стали слишком нишевыми.
11 Mar 2021 в 13:19 #48
Кто-нибуть может обьяснить зачем нам в жизни синусы, косинусы, тангенсы и т.д?