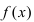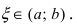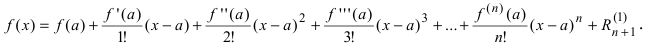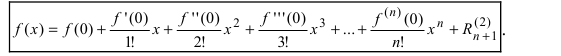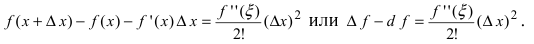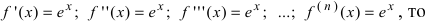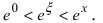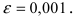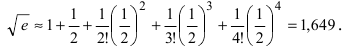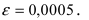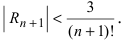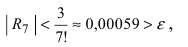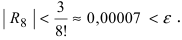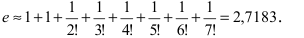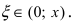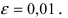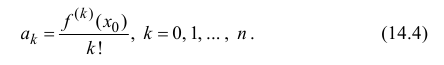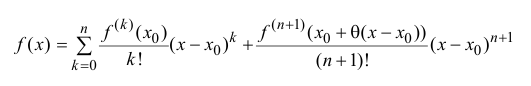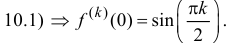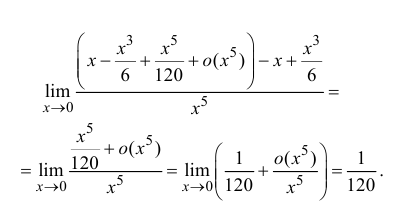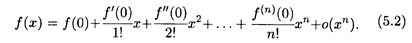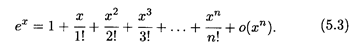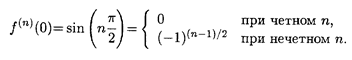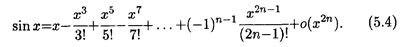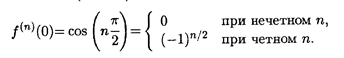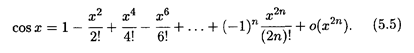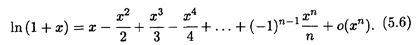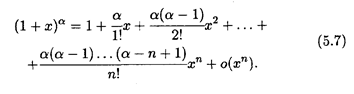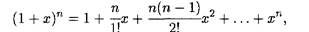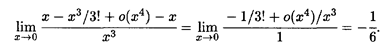для чего нужна формула маклорена
Ряд Тейлора. Ряды Маклорена.
Ряд Тейлора — разложение функции в бесконечную сумму степенных функций.
Ряд Тейлора применяют для апроксимации функции многочленами. То есть, линеаризация уравнений проходит путем разложения в ряд Тейлора и отсечения каждого члена старше 1-го порядка.
Определение ряда Тейлора.
Функция f(x) бесконечно дифференцируется в некоторой окрестности т.a:
Этот ряд называется рядом Тейлора функции f в т.a.
Свойства ряда Тейлора.
Если f есть аналитическая функция во всякой точке a, то ряд Тейлора этой функции во всякой точке a области определения f сходится к f в некоторой окрестности a.
Есть бесконечно дифференцируемые функции, ряд Тейлора которых сходится, однако, при этом отличается от функции во всякой окрестности a. Вариант, предложенный Коши:
У этой функции каждые производные в 0 равны нулю, поэтому коэффициенты ряда Тейлора в точке a=0 равны 0.
Если у функция f(x) есть непрерывные производные вплоть до (n+1)-го порядка, то эту функцию можно разложить в степенной ряд по формуле Тейлора:
где Rn − остаточный член в форме Лагранжа определяют так:
Если это разложение сходится в некотором интервале x, т.е. 
Если a = 0, значит, это разложение является рядом Маклорена:
Ряды Маклорена некоторых функций.
1. Экспонента: 
Формула Тейлора и ее применение с примерами решения
Содержание:
Формула Тейлора и ее применение
Формула Тейлора
Теорема: Если функция
Эта формула была получена в 1715 г. Бруком Тейлором, который был учеником Исаака Ньютона, и носит его имя. Последнее слагаемое в формуле Тейлора 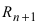
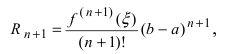
В этой формуле неизвестной является только величина 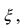
При a = 0 формула Тейлора переходит в формулу Маклoрена:
Пример:
Представить по формуле Маклорена функцию 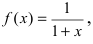
Решение:
Вычислим три первых производных заданной функции:
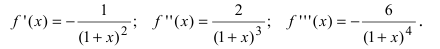
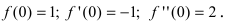
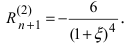
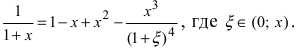
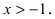
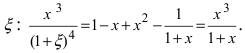
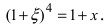
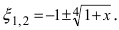
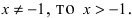
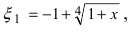
Замечание: При n = 0 формула Тейлора дает формулу конечных приращений:
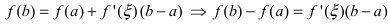
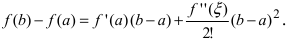
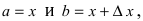
Применение формулы Тейлора
Если известны величины то формула Тейлора позволяет вычислить значение функции в некоторой точке х. В зависимости от требуемой степени точности вычислений достаточно бывает вычислить два, три или несколько первых слагаемых в формуле Тейлора. Для оценки погрешности вычислений необходимо помнить, что величина 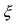
Пример:
Представить функцию 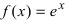
Решение:
Так как 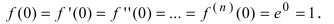
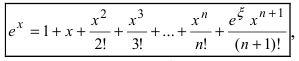
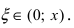
Пример:
Вычислить 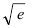
Решение:
Так как основание 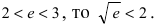
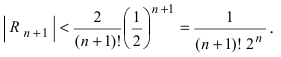
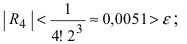
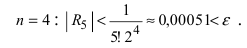
Пример:
Вычислить число е с точностью
Решение:
Согласно результатам, полученным в предыдущем примере, для достижения требуемой точности, подсчитаем остаточный член формулы Маклорена в форме Лагранжа
При n = 6 имеем
при n = 7 получаем
Итак,
Если вычислять значение числа е с точностью 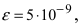
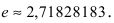
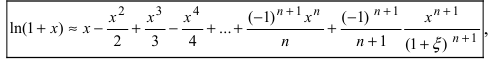
Пример:
Вычислить 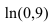
Решение:
Формула тейлора
Пусть функция y=f(x) дифференцируема в точке 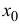
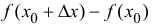
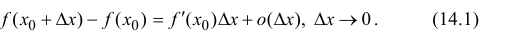
Пусть 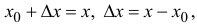
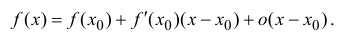
Рассмотрим многочлен 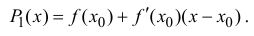
Многочлен 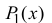
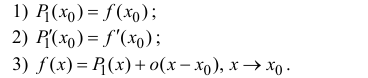
Пусть функция y=f(x) n раз дифференцируема в точке 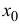
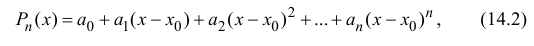
обладающий аналогичными свойствами: 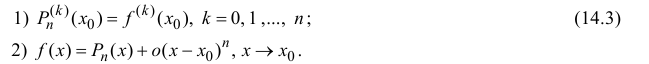
Из (14.2), (14.3) следует, что 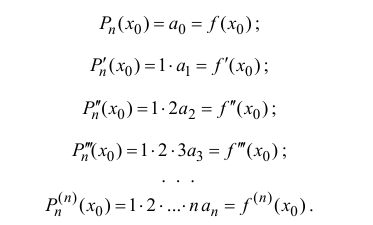
Поэтому коэффициенты 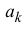
Далее 
Таким образом свойства (14.3) выполняются (при этом коэффициенты
многочлена 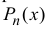
Теорема 14.1. Пусть функция y=f(x) n раз дифференцируема в точке 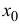
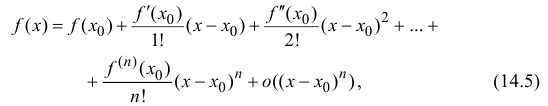
где 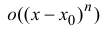
малости, чем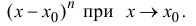
Формула (14.5) называется формулой Тейлора, многочлен 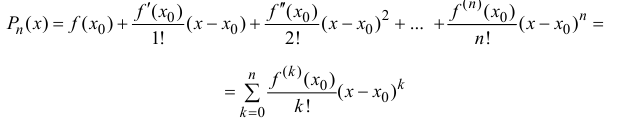
в правой части формулы (14.5) называется многочленом Тейлора, а представление разности 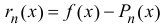
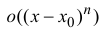
Если функция 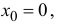
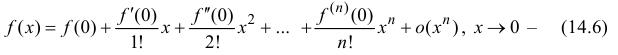
формула Маклорена.
Если функция 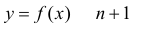
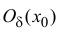
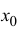
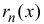
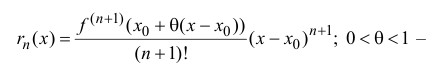
называется формулой Тейлора порядка n с остаточным членом в форме
Лагранжа.
Пример 14.1
В условиях примера 9.4 оценим погрешность вычисления значений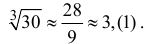
Решение
Запишем формулу Маклорена первого порядка с остаточным членом в форме Лагранжа: 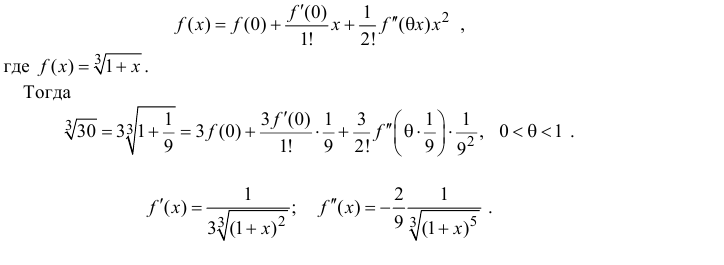
Поэтому
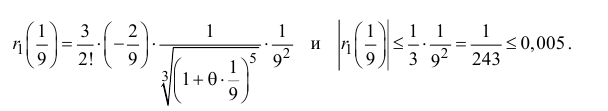
Таким образом, вычисленное значение 3,(1) отличается от истинного с точностью до 0,01.
Пример 14.2
Запишем формулу Маклорена n-го порядка для функции y=sin x: 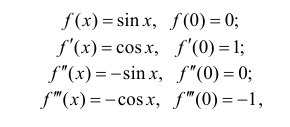
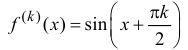
Таким образом, 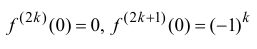
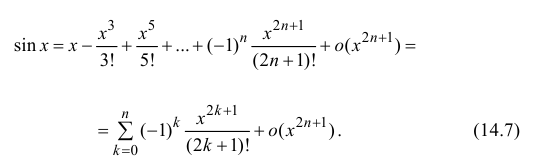
Аналогично 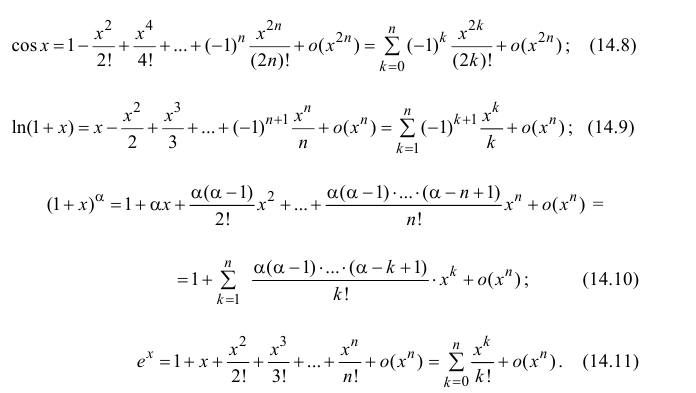
Формулы (14.7)–(14.11) называются основными разложениями.
Пример 14.3
Разложить 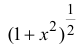
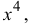
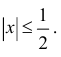
Решение
Пусть 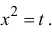
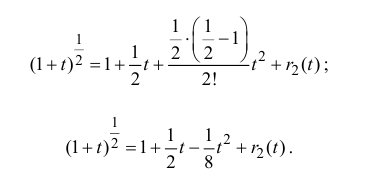
Остаточный член запишем в форме Лагранжа: 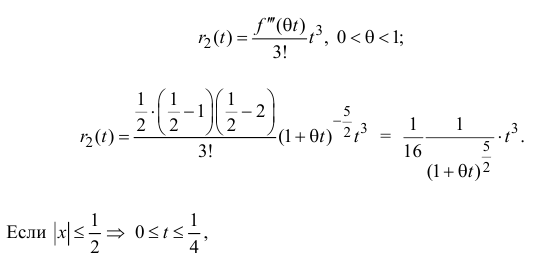
поэтому 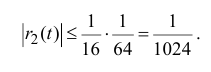
Таким образом, 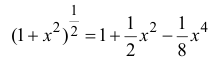
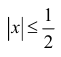
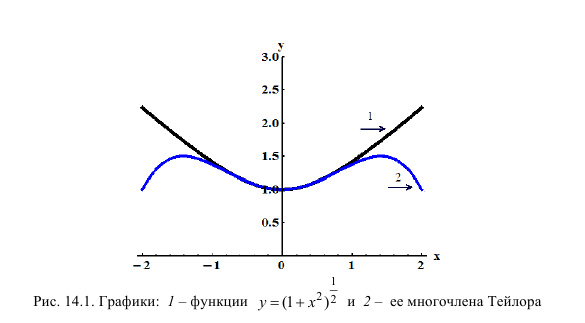
Пример 14.4
Найти 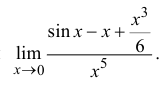
Решение
Воспользуемся разложением (14.7): 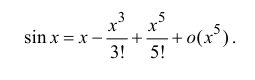
Тогда
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Формула Маклорена
Разложение функций по формуле Маклорена
Одним из основных принципов математики является представление сложного через более простое. Формула Маклорена* как раз и является реализацией этого принципа. Любые функции, дифференцируемые достаточное число раз в точке х = 0, могут быть представлены в виде многочлена некоторой степени. Многочлены же являются наиболее простыми элементарными функциями, над которыми удобно выполнять арифметические действия, вычислять значения в любой точке и т.д.
* Колин Маклорен — шотландский математик (1698 — 1746).
Итак, функцию f(x), имеющую (n + 1) производных в точке х = 0, можно представить по формуле Маклорена вместе с остаточным членом:
Формула (5.2) дает возможность разложить функцию f(x) по формуле Маклорена (в окрестности нуля) или, что то же самое, представить f(x) в виде многочлена, коэффициенты которого вычисляются достаточно просто. Эта формула широко используется и для приближенных вычислений значений различных функций; при этом погрешность вычислений оценивается по остаточному члену о(x n ).
Рассмотрим примеры разложения функций по формуле Маклорена.
Пример 2. f(x) = sin x.
Решение. Нетрудно проверить, что f (n) (x) = sin 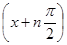
Подстановка в формулу (5.3) приводит к выражению
Пример 3. f(x) = cos x.
Решение. По аналогии с функцией синуса имеем 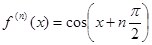
Подстановка в формулу (5.2) приводит к разложению по формуле Маклорена:
Пример 4. f(x) = ln (l + х).
Решение. Так как 
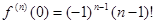
В частном случае, когда α = п — целое число, имеем f (n + l) = 0 и формула (5.7) переходит в формулу бинома Ньютона:
т.е. бином Ньютона является частным случаем формулы Маклорена.
Формула Маклорена в асимптотических формулах и вычислениях пределов функций
Пример 6. Найти 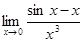
Решение. Применяя формулу (5.2) при п = 2, получаем
Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет
Формула Тейлора
Формула Тейлора с остаточным членом в форме Лагранжа.
Если функция \(f(x)\) имеет в точке \(x_<0>\) производную n-го порядка, то существует многочлен \(P_
$$
P_n(x_0)=f(x_<0>),\ P_
$$
Этот многочлен представляется в виде
$$
P_n(x)=f(x_<0>)+\frac
$$
\(\circ\) Пусть \(\varphi(x)=(x-x_0)^m\), где \(m\in\mathbb
$$
\varphi^<(k)>(x_<0>)=\left\<\begin
0, & если \ k\neq m,\\
k!, & если \ k=m.
\end
$$
Из \eqref
Пусть функции \(f(x)\) и \(\psi(x)\) определены в \(\delta\)-окрестности точки \(x_0\) и удовлетворяют следующим условиям:
Тогда для каждого \(x\in\dot_<\delta>(x_<0>)\) существует точка \(\xi\), принадлежащая интервалу с концами \(x_0\) и \(x\) такая, что
$$
\frac<\varphi(x)><\psi(x)>=\frac<\varphi^<(n+1)>(\xi)><\psi^<(n+1)>(\xi)>.\label
$$
\(\circ\) Пусть, например, \(x\in(x_0,x_0+\delta)\). Тогда, применяя к функциям \(\varphi\) и \(\psi\) на отрезке \([x_0,x]\) теорему Коши и учитывая, что \(\varphi(x_0)=\psi(x_0)=0\) в силу условий \eqref
$$
\frac<\varphi(x)><\psi(x)>=\frac<\varphi(x)-\varphi(x_0)><\psi(x)-\psi(x_0)>=\frac<\varphi'(\xi_1)><\psi'(\xi_1)>\quad x_0 Теорема 1.
Пусть существует \(\delta >0\) такое, что функция \(f(x)\) имеет в \(\delta\)-окрестности точки \(x_0\) производные до \((n+1)\)-го порядка включительно.
Тогда для любого \(x\in\dot_\delta(x_0)\) найдется точка \(\xi\), принадлежащая интервалу \(\Delta\) с концами \(x_<0>\) и \(x\), такая, что
$$
f(x)=f(x_0)+\frac
$$
\(\circ\) Пусть \(x\in\dot_\delta(x_0)\), \(P_n(x)=\displaystyle \sum_
$$
r_
$$
Так как многочлен \(P_
$$
r_n(x_0)=r_n'(x_0)=\ldots=r_
$$
Рассмотрим функции \(\varphi(x)=r_n(x)\), \(\psi(x)=(x-x_0)^
$$
\frac<\varphi(x)><\psi(x)>=\frac
$$
так как \(P_n^<(n+1)>(x)\equiv 0,\ \psi^<(n+1)>(x)=(n+1)!\) Из равенств \eqref
Функцию \(r_n(x)=\displaystyle \frac
Если функции \(\varphi\) и \(\psi\) дифференцируемы \(n\) раз при \(x\geq x_<0>\) и удовлетворяют условиям \(\varphi^<(k)>(x_<0>)=\psi^<(k)>(x_<0>)\), \(k=\overline<0,n-1>\), \(\varphi^<(n)>(x)>\psi^<(n)>(x)\) при \(x > x_0\), то \(\varphi(x) > \psi(x)\) при \(x > x_<0>\).
\(\circ\) Для \(n=1\) утверждение доказано ранее (следствие 4 из теоремы Лагранжа). Обозначим \(f(x)=\varphi(x)-\psi(x)\). Тогда \(f^<(k)>(x_<0>)=0\) при \(k=\overline<0,n-1>0\), и по формуле \eqref
$$
f(x)=\frac<1>
$$
Если \( x> x_<0>\), то \(\xi > x_0\), \(f^<(n)>(\xi)=\varphi^<(n)>(\xi)-\psi^<(n)>(\xi) > 0\), и поэтому \(f(x) > 0\), то есть \(\varphi(x) > \psi(x)\) при \(x > x_<0>\). \(\bullet\)
Формула Тейлора с остаточным членом в форме Пеано.
Из существования \(f^<(n)>(x_0)\) следует, что функция \(f(x)\) определена и имеет производные до \((n-1)\)-го порядка включительно в \(\delta\)-окрестности точки \(x_0\). Обозначим \(\varphi(x)=r_n(x)\), \(\psi(x)=(x-x_0)^n\), где функция \(r_n(x)\) определяется формулой \eqref
$$
\frac
$$
где \(\xi=\xi(x)\) и
$$
x_0 Замечание 2.
Формулу \eqref
Разложить функцию \(f(x)\) по формуле Тейлора в окрестности точки \(x_0\) до \(o((x-x_0)^n)\) — значит представить ее в виде \eqref
\(\circ\) По теореме 2 справедлива формула \eqref
$$
a_0+a_1(x-x_0)+\ldots+a_n(x-x_0)^n+o((x-x_0)^n)=\\=f(x_<0>)+f'(x_<0>)(x-x_0)+\ldots+f^<(n)>(x_<0>)\frac<(x-x_<0>)^
$$
Переходя к пределу при \(x\rightarrow x_<0>\) в равенстве \eqref
$$
a_1+a_2(x-x_0)+\ldots+a_n(x-x_0)^
$$
Переходя в этом равенстве к пределу при \(x\rightarrow x_0\), находим \(f'(x_<0>)=a_<1>\). Продолжая эти рассуждения, получаем равенства \eqref
Теорема 3 означает, что представление в виде \eqref
Разложить функцию \(\displaystyle \frac<1><1-x>\) по формуле Тейлора в окрестности точки \(x_<0>=0\) до \(o(x^
\(\triangle\) Воспользуемся равенством \((1+x+\ldots+x^
$$
\frac<1><1-x>=1+x+\ldots+x^n+o(x^n).\label
$$
Так как функция \(\displaystyle \frac<1><1-x>\) бесконечно дифференцируема при \(x\neq 1\) (имеет производные любого порядка), то по теореме 3 формула \eqref
Разложение основных элементарных функций по формуле Тейлора.
Если \(x_<0>=0\) и существует \(f^<(n)>(0)\), то равенство \eqref
$$
f(x)=\sum_
$$
Формулу \eqref
Пусть, функция \(f(x)\) бесконечно дифференцируема на интервале \((-l,l)\). Если эта функция является четной, то ее производная — нечетная функция, и, наоборот, производная нечетной функции — четная функция (мы уже разбирали этот пример). Отсюда следует, что для нечетной функции \(f\) выполняются условия \(f^<(2k)>(0)=0\), \(k\in\mathbb
Поэтому формулу \eqref
$$
f(x)=\sum_
$$
а для нечетной функции — в виде
$$
f(x)=\sum_
$$
В формуле \eqref
Показательная функция.
Гиперболические функции.
Так как \(\operatorname