для чего нужна функция активации в нейросети
Практики реализации нейронных сетей
Содержание
Аугментация данных [ править ]
При глубоком обучении иногда можно столкнуться с ситуацией, когда набор данных имеет ограниченный размер. Но чтобы получить лучшие результаты обобщение модели, необходимо иметь больше данных, в том числе и различные их вариации. То есть необходимо увеличить размер исходного набора искусственным образом, и это можно сделать с помощью аугментации данных.
| Определение: |
| Аугментация данных (англ. data augmentation) — это методика создания дополнительных данных из имеющихся данных. |
Чаще всего, проблема ограниченного набора данных возникает при решении задач, связанных с обработкой изображений. Следующие способы аугментации изображений являются самыми популярными:
Также, можно применять различные комбинации, к примеру, вырезать часть изображения, повернуть его и изменить цвет фона.
Продвинутыми способами аугментации данных является семейство порождающих состязательных сетей.
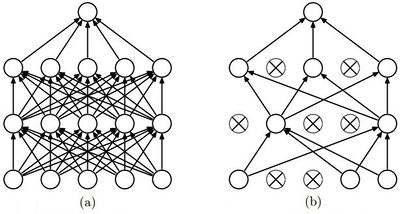
Дропаут [ править ]
Одной из проблем глубокого обучения нейронных сетей является переобучение. И метод дропаут — популярный способ решения этой проблемы, благодаря простому алгоритму и хорошим практическим результатам.
| Определение: |
| Дропаут (англ. dropout) — метод регуляризации нейронной сети для предотвращения переобучения. |
В обычной нейронной сети явление переобучения появляется из-за так называемой совместной адаптации (англ. co-adaptation), то есть при обновлении весов нейрона, во время обучения методом обратного распространения ошибки, учитывается деятельность остальных нейронов с целью минимизировать функцию потерь. Поэтому веса нейронов могут меняться, исправляя при этом ошибки других нейронов. Метод дропаута как раз предотвращает эту адаптацию.
Алгоритм дропаут [ править ]
Обратный дропаут [ править ]
Обратная модификация дропаута на практике используется чаще обычной, потому что в ней не нужно менять каждый раз модель для проведения этапа тестирования.
Функции активации [ править ]
Одним из важнейших аспектов глубокой нейронной сети являются функции активации.
| Определение: |
| Функция активации (англ. activation function) [math]a(x)[/math] определяет выходное значение нейрона в зависимости от результата взвешенной суммы входов и порогового значения. |
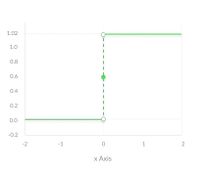
Ступенчатая функция [ править ]
Ступенчатая функция (англ. binary step function) является пороговой функцией активации. То есть если [math]z[/math] больше или меньше некоторого значения, то нейрон становится активированным. Такая функция отлично работает для бинарной классификации. Но она не работает, когда для классификации требуется большее число нейронов и количество возможных классов больше двух.
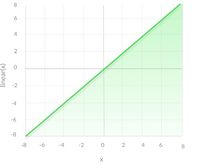
Линейная функция [ править ]
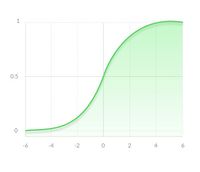
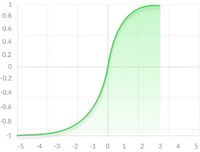
Сигмоидная функция [ править ]
Несмотря на множество сильных сторон сигмоидной функции, у нее есть значительный недостаток. Производная такой функции крайне мала во всех точках, кроме сравнительно небольшого промежутка. Это сильно усложняет процесс улучшения весов с помощью градиентного спуска. Более того, эта проблема усугубляется в случае, если модель содержит много слоев. Данная проблема называется проблемой исчезающего градиента. [1]
Что касается использования сигмоидной функции, то ее преимущество над другими — в нормализации выходного значения. Иногда, это бывает крайне необходимо. К примеру, когда итоговое значение слоя должно представлять вероятность случайной величины. Кроме того, эту функцию удобно применять при решении задачи классификации, благодаря свойству «прижимания» к асимптотам.
Функция гиперболического тангенса [ править ]
Обычно, [math]tanh[/math] является предпочтительнее сигмоиды в случаях, когда нет необходимости в нормализации. Это происходит из-за того, что область определения данной функции активации центрирована относительно нуля, что снимает ограничение при подсчете градиента для перемещения в определенном направлении. Кроме того, производная гиперболического тангенса значительно выше вблизи нуля, давая большую амплитуду градиентному спуску, а следовательно и более быструю сходимость.
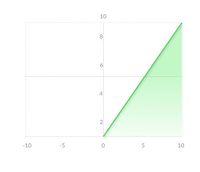
Функция ReLU [ править ]
Функцию активации ReLU следует использовать, если нет особых требований для выходного значения нейрона, вроде неограниченной области определения. Но если после обучения модели результаты получились не оптимальные, то стоит перейти к другим функциям, которые могут дать лучший результат.
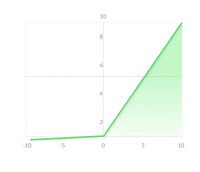
Функция Leaky ReLU [ править ]
На практике LReLU используется не так часто. Практический результат использования LReLU вместо ReLU отличается не слишком сильно. Однако в случае использования Leaky требуется дополнительно настраивать гиперпараметр (уровень наклона при отрицательных значениях), что требует определенных усилий. Еще одной проблемой является то, что результат LReLU не всегда лучше чем при использовании обычного ReLU, поэтому чаще всего такой подход используют как альтернатива. Довольно часто на практике используется PReLU (Parametric ReLU), который позволяет добиться более значительных улучшений по сравнению с ReLU и LReLU. Также, в случае параметрической модификации ReLU, угол наклона не является гиперпараметром и настраивается нейросетью.
Функция активации (Activation Function)
Функция активации – это фрагмент программного кода, добавляемый в искусственную Нейронную сеть (Neural Network), чтобы помочь ей изучить сложные закономерности данных. В сравнении с нейронами нашего мозга, Функция (Function) активации решает, что должно быть запущено в следующий нейрон. Она принимает выходной сигнал из предыдущей ячейки и преобразует его в некоторую форму, которую можно использовать в качестве входных данных для следующей ячейки. На изображении ниже – устройство нейрона человеческого мозга (слева) и искусственного. Аксон – это отросток нейрона, по которому идут импульсы к иннервируемым органам и другим нервным клеткам:
Зачем это нужно?
Существует несколько причин для использования нелинейных функций активации:
Значение Смещения (Bias), если не ограничиваться определенным пределом, может быть очень большим, особенно в случае глубоких нейронных сетей, которые имеют миллионы параметров. Это может привести к вычислительным проблемам. Существуют некоторые функции активации (например, Softmax), которые выводят определенные значения для бинарных входных значений (0 или 1).
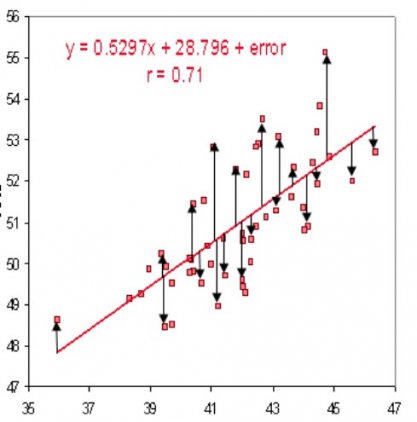
Линейный классификатор, использующий три характеристики (вес, систолическое артериальное давление и возраст на рисунке выше), может дать нам линию в трехмерном пространстве, но он никогда не сможет точно изучить закономерность, которая делает человека курильщиком или некурящим, потому что шаблон, который определяет эту классификацию, просто не является линейным. Если мы используем Искусственную нейронную сеть (ANN) с одной ячейкой, но без функции активации, то «предсказывающее» уравнение равно W * x + b, что бесполезно, ибо W * x также имеет степень, равную 1 (x просто не возводится в степень), следовательно, это линейный классификатор.
Однако сложения слоев недостаточно, особенно для высокоуровневых проблем, например, Компьютерного зрения (CV) или Обработкой естественного языка (NLP).
Чтобы модель получила возможность (или более высокую степень сложности) изучать нелинейные паттерны, между ними добавляются определенные нелинейные уровни – функции активации.
Желательные особенности функции активации
Сигмоид – одна из нелинейных функции активации:
Эта функция активации используется только по историческим причинам и никогда не используется в реальных Моделях (Model). Это затратно с точки зрения вычислений, вызывает проблему исчезающего градиента и не имеет нулевого центра. Этот метод обычно используется для задач Двоичной классификации (Binary Classification).
Зачем нейронным сетям нужна функция активации?
Дата публикации Jul 1, 2019
Зачем нейронным сетям нужна функция активации? Всякий раз, когда вы впервые видите архитектуру нейронной сети, первое, что вы заметите, это много взаимосвязанных слоев.
Каждый слой в нейронной сети имеет функцию активации, но зачем они нужны? И почему они так важны? Узнайте ответ здесь.
Что такое функции активации?
Чтобы ответить на вопрос о том, что такое функции активации, давайте сначала сделаем шаг назад и ответим на более крупный вопрос: что такое нейронная сеть?
Что такое нейронные сети?
Это означает, что, учитывая набор наблюдаемых экземпляров с определенными значениями, которые мы хотим предсказать, и некоторые данные, которые мы имеем для каждого экземпляра, он попытается обобщить эти данные, чтобы он мог правильно предсказать значения для новых случаев проблемы.
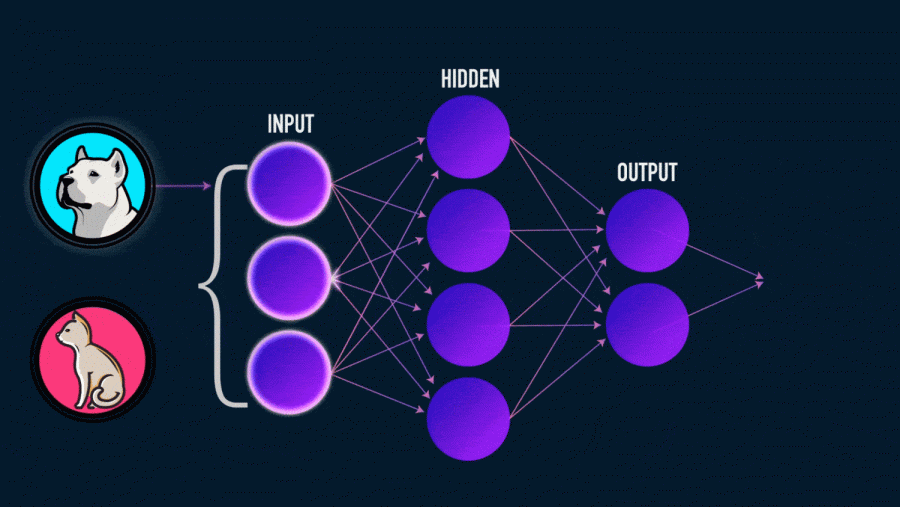
В качестве примера мы можем разработать классификатор изображений (обычно сСверточная нейронная сеть). Здесь входные данные представляют собой вектор пикселей. Выходными данными может быть числовая метка класса (например, 1 для собак, 0 для кошек).
Это научит нейронную сеть предсказывать, содержит ли изображение кошку или собаку.
Придумать математическую функцию, которая выполняла это вручную, было бы невозможно.Для человека,
Поэтому мы изобрели Машину, которая нашла эту функцию для нас.
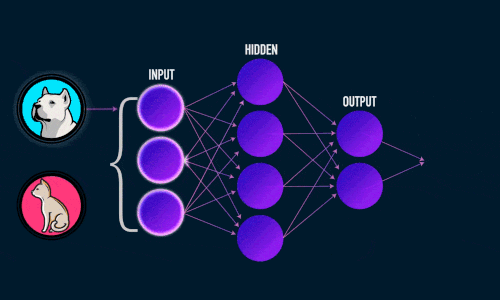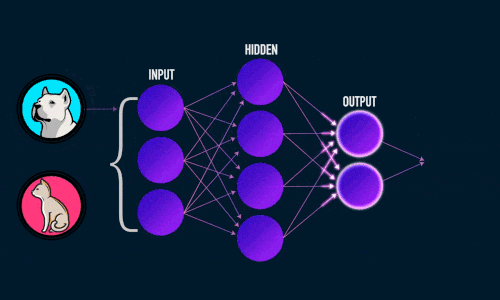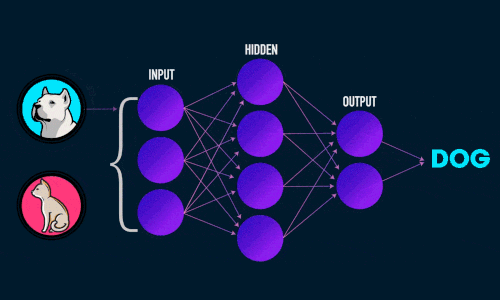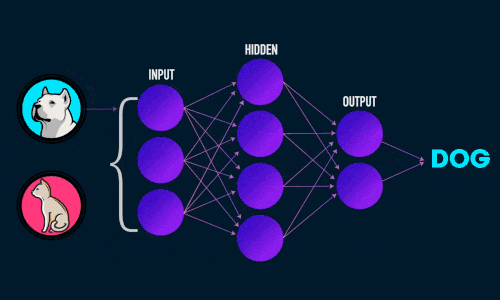
Это выглядит примерно так:
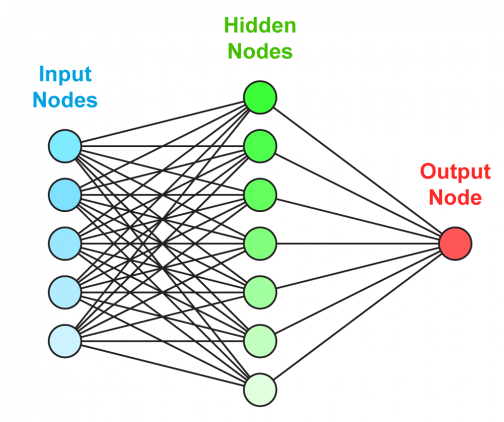
Но вы, возможно, видели эту картину много раз, узнаете ее для нейронной сети и все еще не знаете точно, что она представляет.
Здесь каждый круг представляет нейрон в нашей нейронной сети, а вертикально выровненные нейроны представляют каждый слой.
Как работают нейронные сети?
Нейрон это простоматематическая функция, который принимает входы (выходы нейронов, указывающие на него) ивозвращает выводы,
Эти выходные данные служат входными данными для следующего уровня и так далее, пока мы не доберемся до конечного выходного уровня, который является фактическим значением, которое мы возвращаем.
Существует входной слой, где каждый нейрон просто возвращает соответствующее значение в векторе входных данных.
Целью нейронной сети для каждого набора входов является создание каждого из ее выходов.как можно ближе к фактическим ожидаемым значениям,
Опять вспомним пример классификатора изображений.
Если в качестве входных данных взять изображения животных размером 100×100 пикселей, то в нашем входном слое будет 30000 нейронов. Это 10000 для всех пикселей, умноженное на три, поскольку пиксель уже является тройным вектором (значения RGB).
Затем мы запустим входные данные через каждый слой. Мы получаемновый вектор как выход каждого слоя, подайте его на следующий слой в качестве входных данных, и так далее.
Каждый нейрон в слое будет возвращать одно значение, поэтому выходной вектор слоя будет иметь столько измерений, сколько у слоя есть нейроны.
Итак, какое значение вернет нейрон, учитывая некоторые входные данные?
Что делает нейрон?
Нейрон возьмет входной вектор и сделает с ним три вещи:
И мы наконец-то добрались до сути нашего бизнеса: это то, что делают функции активации.
Мы обычно используемнелинейные функции как функции активации, Это потому, что линейная часть уже обработана ранее примененным продуктом и дополнением.
Каковы наиболее часто используемые функции активации?
Я говорю о нелинейных функциях, и это звучит достаточно логично, но каковы типичные, часто используемые функции активации?
Давайте посмотрим несколько примеров.
ReLU означает «Выпрямленный линейный блок».
Из всех функций активации это тот, которыйнаиболее похож на линейный:
В математических словах
Это означает, что все отрицательные значения станут 0, в то время как остальные значения останутся без изменений.
Это биологически вдохновленная функция, так как нейроны в мозге будут либо «запускать» (возвращать положительное значение), либо нет (возвращать 0).
Обратите внимание, как в сочетании с уклоном, это на самом делеотфильтровывает любое значение ниже определенного порога,
сигмоид
Сигмовидная функция принимает любое действительное число в качестве входных данных, ивозвращает значение от 0 до 1, Поскольку оно непрерывно, оно эффективноsmushes» значения:
То же самое происходит в отрицательном направлении, за исключением того, что оно сходится к 0.
Вот математическая формула для сигмовидной функции.
Как видите, он приближается к 1, когда x приближается к бесконечности, и приближается к 0, если x приближается к минус бесконечность.
Он также симметричен и имеет значение 1/2, когда его вход равен 0.
Поскольку она принимает значения от 0 до 1, эта функция чрезвычайно полезна в качестве выходных данных, если вы хотите смоделировать вероятность.
Также полезно, если вы хотите применить «фильтр», чтобы частично сохранить определенное значение (как вLSTM забыли ворота).
Зачем нейронным сетям нужна функция активации?
Мы уже говорили о приложениях, которые имеют разные функции активации в разных случаях.
Некоторые пропускают сигнал или препятствуют ему, другие фильтруют его интенсивность. Там дажеTANHФункция активации: вместо фильтрации она превращает свой вход в отрицательное или положительное значение.
Но зачем нашим нейронным сетям нужны функции активации?Что случилось бы, если бы мы не использовали их?
Я нашел объяснение этого вопроса в удивительном Йошуа БенжиоКнига глубокого обученияи я думаю, что это прекрасно объясняется там.
Мы могли бы вместо того, чтобы составлять наши линейные преобразования с помощью нелинейных функций, заставить каждый нейрон просто возвращать свой результат (вместо этого эффективно объединяя их с тождеством).
Но тогда все наши слои будут просто складывать одно аффинное (продукт плюс сложение) преобразование за другим. Каждый слой просто добавляет векторный продукт и векторное добавление к предыдущему.
Можно показать (и вы даже можете убедить себя, если попробуете математику с маленьким вектором на доске), что эта композиция аффинных преобразований эквивалентна одному аффинному преобразованию.
По сути, вся эта «нейронная сеть», где все функции активации были заменены идентификатором, была быне что иное, как векторный продукт и сложение смещения,
Есть много проблем, которые линейное преобразование не может решить, поэтому мы бысокращение количества функцийнаша модель могла бы оценить.
В качестве очень простого, но потрясающего примера рассмотрим оператор XOR.
Попробуйте найти двухэлементный вектор плюс смещение, которое может взять x1 и x2, и превратить их в x1 XOR x2. Давай, я подожду.
Точно, вы не можете. никто не может. Тем не менее, рассмотрим
Если вы работаете с математикой, вы увидите, что она имеет желаемый результат для каждой возможной комбинации 1 и 0.
Поздравляем! Вы только что обучили свою первую нейронную сеть!
И это стало проблемой, о которой линейная модель никогда бы не узнала.
Выводы
Я надеюсь, что после этого объяснения вы теперь лучше поймете, почему нейронным сетям нужна функция активации.
В будущих статьях я могу рассказать о других функциях активации и их использовании, таких как SoftMax и спорный Cos.
Так что ты думаешь? Вы узнали что-нибудь из этой статьи? Вы нашли это интересным? Была ли математика выключена?
Не стесняйтесь связаться со мной пощебет,среднийилиdev.toза все, что вы хотите сказать или попросить меня!
Если вы хотите повысить свой уровень в качестве ученого данных, проверьте мойлучшие книги по машинному обучениюсписок и мойУчебник Bash,
Как работает нейронная сеть: алгоритмы, обучение, функции активации и потери
Нейронная сеть — попытка с помощью математических моделей воспроизвести работу человеческого мозга для создания машин, обладающих искусственным интеллектом.
Искусственная нейронная сеть обычно обучается с учителем. Это означает наличие обучающего набора (датасета), который содержит примеры с истинными значениями: тегами, классами, показателями.
Неразмеченные наборы также используют для обучения нейронных сетей, но мы не будем здесь это рассматривать.
Например, если вы хотите создать нейросеть для оценки тональности текста, датасетом будет список предложений с соответствующими каждому эмоциональными оценками. Тональность текста определяют признаки (слова, фразы, структура предложения), которые придают негативную или позитивную окраску. Веса признаков в итоговой оценке тональности текста (позитивный, негативный, нейтральный) зависят от математической функции, которая вычисляется во время обучения нейронной сети.
Раньше люди генерировали признаки вручную. Чем больше признаков и точнее подобраны веса, тем точнее ответ. Нейронная сеть автоматизировала этот процесс.
Искусственная нейронная сеть состоит из трех компонентов:
Обучение нейросетей происходит в два этапа:
Во время прямого распространения ошибки делается предсказание ответа. При обратном распространении ошибка между фактическим ответом и предсказанным минимизируется.
Прямое распространение ошибки
Зададим начальные веса случайным образом:
Умножим входные данные на веса для формирования скрытого слоя:
Выходные данные из скрытого слоя передается через нелинейную функцию (функцию активации), для получения выхода сети:
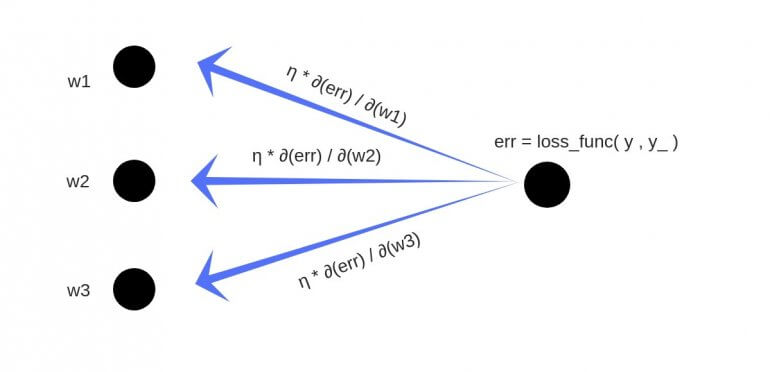
Обратное распространение
Полученный результат затем вычитается из соответствующих весов.
В результате получатся следующие обновленные веса:
То, что мы предполагаем и инициализируем веса случайным образом, и они будут давать точные ответы, звучит не вполне обоснованно, тем не менее, работает хорошо.

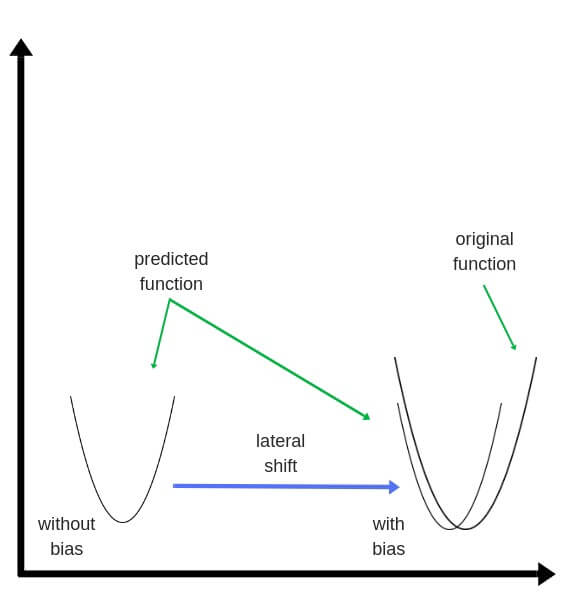
Смещения – это веса, добавленные к скрытым слоям. Они тоже случайным образом инициализируются и обновляются так же, как скрытый слой. Роль скрытого слоя заключается в том, чтобы определить форму базовой функции в данных, в то время как роль смещения – сдвинуть найденную функцию в сторону так, чтобы она частично совпала с исходной функцией.
Частные производные
Частные производные можно вычислить, поэтому известно, какой был вклад в ошибку по каждому весу. Необходимость производных очевидна. Представьте нейронную сеть, пытающуюся найти оптимальную скорость беспилотного автомобиля. Eсли машина обнаружит, что она едет быстрее или медленнее требуемой скорости, нейронная сеть будет менять скорость, ускоряя или замедляя автомобиль. Что при этом ускоряется/замедляется? Производные скорости.
Разберем необходимость частных производных на примере.
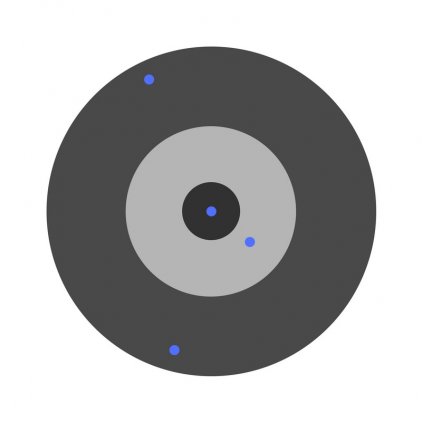
Предположим, детей попросили бросить дротик в мишень, целясь в центр. Вот результаты:
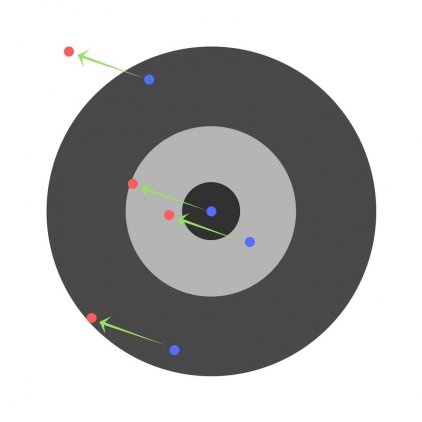
Теперь, если мы найдем общую ошибку и просто вычтем ее из всех весов, мы обобщим ошибки, допущенные каждым. Итак, скажем, ребенок попал слишком низко, но мы просим всех детей стремиться попадать в цель, тогда это приведет к следующей картине:
Ошибка нескольких детей может уменьшиться, но общая ошибка все еще увеличивается.
Найдя частные производные, мы узнаем ошибки, соответствующие каждому весу в отдельности. Если выборочно исправить веса, можно получить следующее:
Гиперпараметры
Нейронная сеть используется для автоматизации отбора признаков, но некоторые параметры настраиваются вручную.
Скорость обучения (learning rate)
Скорость обучения является очень важным гиперпараметром. Если скорость обучения слишком мала, то даже после обучения нейронной сети в течение длительного времени она будет далека от оптимальных результатов. Результаты будут выглядеть примерно так:
С другой стороны, если скорость обучения слишком высока, то сеть очень быстро выдаст ответы. Получится следующее:
Функция активации (activation function)
Функция активации — это один из самых мощных инструментов, который влияет на силу, приписываемую нейронным сетям. Отчасти, она определяет, какие нейроны будут активированы, другими словами и какая информация будет передаваться последующим слоям.
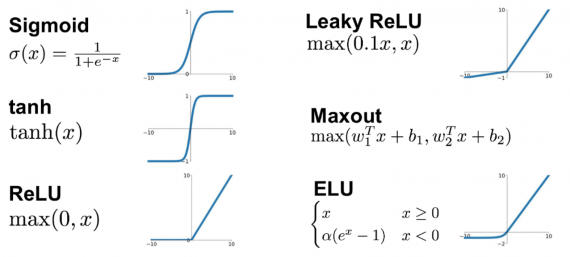
Без функций активации глубокие сети теряют значительную часть своей способности к обучению. Нелинейность этих функций отвечает за повышение степени свободы, что позволяет обобщать проблемы высокой размерности в более низких измерениях. Ниже приведены примеры распространенных функций активации:
Функция потери (loss function)
Функция потерь находится в центре нейронной сети. Она используется для расчета ошибки между реальными и полученными ответами. Наша глобальная цель — минимизировать эту ошибку. Таким образом, функция потерь эффективно приближает обучение нейронной сети к этой цели.
Функция потерь измеряет «насколько хороша» нейронная сеть в отношении данной обучающей выборки и ожидаемых ответов. Она также может зависеть от таких переменных, как веса и смещения.
Функция потерь одномерна и не является вектором, поскольку она оценивает, насколько хорошо нейронная сеть работает в целом.
Некоторые известные функции потерь:
Cреднеквадратичное отклонение – самая простая фукция потерь и наиболее часто используемая. Она задается следующим образом:
Функция потерь в нейронной сети должна удовлетворять двум условиям:
Глубокие нейронные сети
Глубокое обучение (deep learning) – это класс алгоритмов машинного обучения, которые учатся глубже (более абстрактно) понимать данные. Популярные алгоритмы нейронных сетей глубокого обучения представлены на схеме ниже.
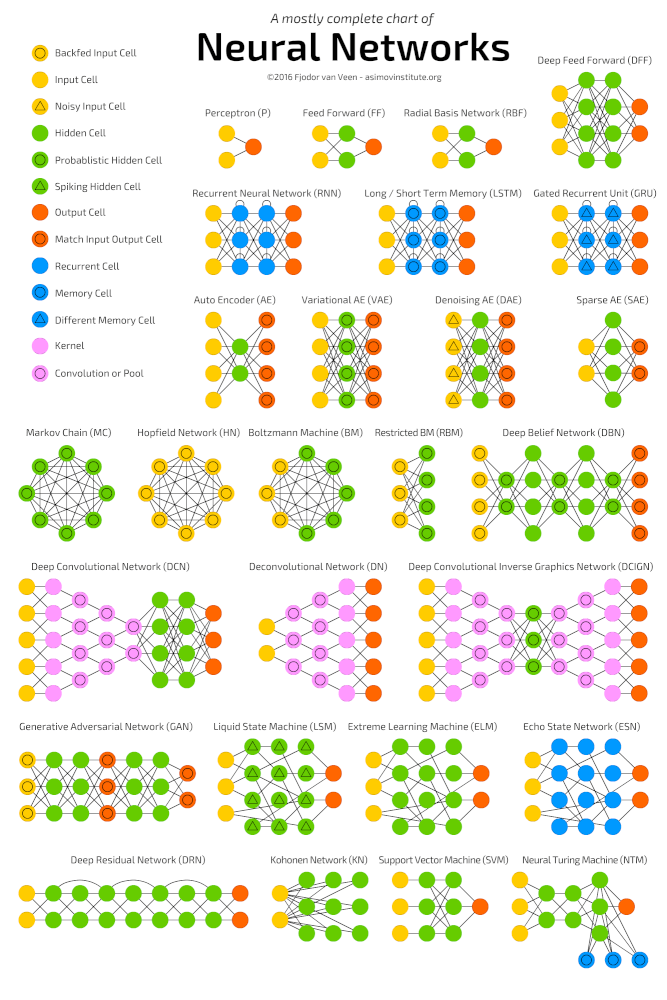
Более формально в deep learning:
Пример
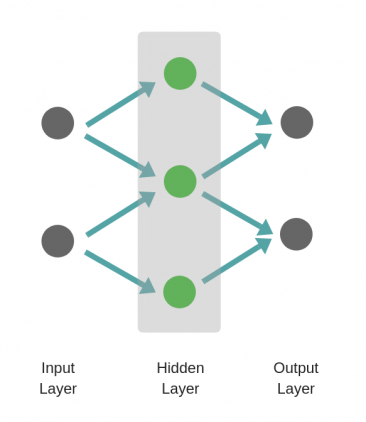
Рассмотрим однослойную нейронную сеть:
Здесь, обучается первый слой (зеленые нейроны), он просто передается на выход.
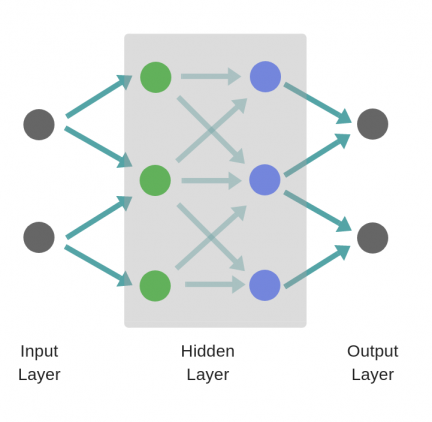
В то время как в случае двухслойной нейронной сети, независимо от того, как обучается зеленый скрытый слой, он затем передается на синий скрытый слой, где продолжает обучаться:
Следовательно, чем больше число скрытых слоев, тем больше возможности обучения сети.
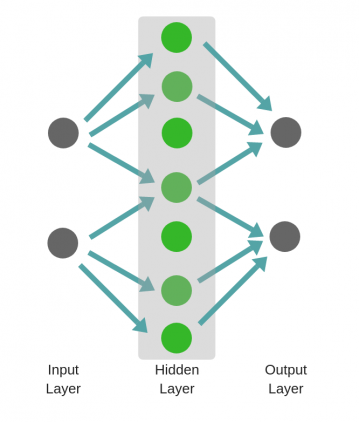
Не следует путать с широкой нейронной сетью.
В этом случае большое число нейронов в одном слое не приводит к глубокому пониманию данных. Но это приводит к изучению большего числа признаков.
Изучая английскую грамматику, требуется знать огромное число понятий. В этом случае однослойная широкая нейронная сеть работает намного лучше, чем глубокая нейронная сеть, которая значительно меньше.
В случае изучения преобразования Фурье, ученик (нейронная сеть) должен быть глубоким, потому что не так много понятий, которые нужно знать, но каждое из них достаточно сложное и требует глубокого понимания.
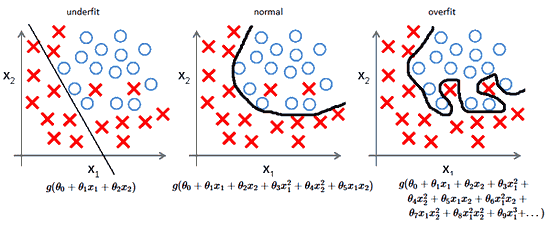
Главное — баланс
Очень заманчиво использовать глубокие и широкие нейронные сети для каждой задачи. Но это может быть плохой идеей, потому что:
Проклятье размерности
Проклятие размерности относится к различным явлениям, возникающим при анализе и организации данных в многомерных пространствах (часто с сотнями или тысячами измерений), и не встречается в ситуациях с низкой размерностью.
Грамматика английского языка имеет огромное количество аттрибутов, влияющих на нее. В машинном обучении мы должны представить их признаками в виде массива/матрицы конечной и существенно меньшей длины (чем количество существующих признаков). Для этого сети обобщают эти признаки. Это порождает две проблемы:
Компромисс
На ранней стадии обучения смещение велико, потому что выход из сети далек от желаемого. А дисперсия очень мала, поскольку данные имеет пока малое влияние.
В конце обучения смещение невелико, потому что сеть выявила основную функцию в данных. Однако, если обучение слишком продолжительное, сеть также изучит шум, характерный для этого набора данных. Это приводит к большому разбросу результатов при тестировании на разных множествах, поскольку шум меняется от одного набора данных к другому.
алгоритмы с большим смещением обычно в основе более простых моделей, которые не склонны к переобучению, но могут недообучиться и не выявить важные закономерности или свойства признаков. Модели с маленьким смещением и большой дисперсией обычно более сложны с точки зрения их структуры, что позволяет им более точно представлять обучающий набор. Однако они могут отображать много шума из обучающего набора, что делает их прогнозы менее точными, несмотря на их дополнительную сложность.
Следовательно, как правило, невозможно иметь маленькое смещение и маленькую дисперсию одновременно.
Сейчас есть множество инструментов, с помощью которых можно легко создать сложные модели машинного обучения, переобучение занимает центральное место. Поскольку смещение появляется, когда сеть не получает достаточно информации. Но чем больше примеров, тем больше появляется вариантов зависимостей и изменчивостей в этих корреляциях.