для чего нужна таблица брадиса

Здесь четырехзначные математические онлайн таблицы для таких тригонометрических функций как: синусы, косинусы, кроме того вы на нашем сайте вы сможете найти подобные таблицы для тангенсов и котангенсов.

Как пользоваться таблицей Брадиса.

На некоторых примерах рассмотрим, как пользоваться таблицей Брадиса.

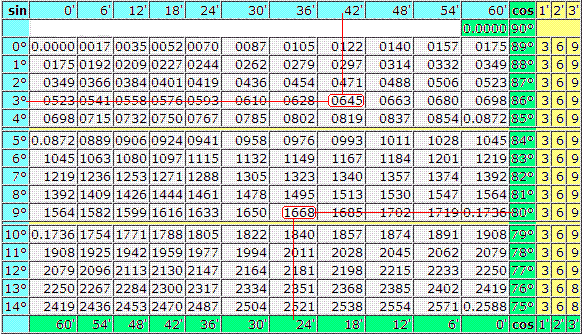
sin 7° = 0.1219 (косинусы находятся внизу) cos 82° = 0.1392.

sin 3°42′ = 0.0645 (ниже на изображении отмечено красным) cos 80°24′ = 0.1668.

Обратите внимание, все тоже самое верно и при определении значений тангенса и котангенса.

Далее рассмотрим вариант посложнее, когда угол, который представлен в таблице не указан, значит, нужно выбирать более близкое к нему значение (из значений, которые указаны в таблице синусов и косинусов), а на разницу, которая может составлять 1′,2′,3′, берем поправку из минут (желтая графа), как видно на примере:

sin 3°45′=sin 3°42′+3′=0.0645+0.0009=0.0654 либо

sin 3°45′=sin 3°48′−3′=0.0663−0.0009=0.0654

Кроме того, нужно помнить правило: для синуса у поправки неотрицательный знак, а у косинуса неположительный.

cos 80°27′=80°24′+3′=0.1668+(-0.0009)=0.1659 либо

Таблица Брадиса.

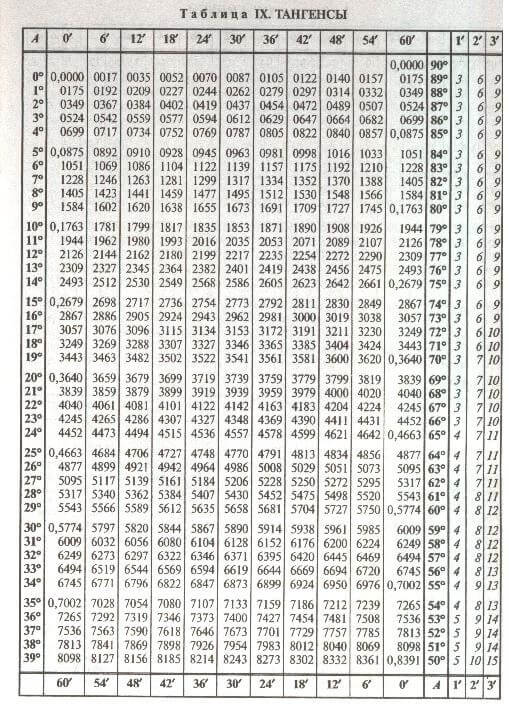
Таблица разбита на 2 части. В 1-ой части таблицы Брадиса тангенсы от 0° до 75° и котангенсы от 15° до 90° определяются с помощью дополнительных столбиков для 1’, 2’ и 3’ (минуты). Во 2-ой части тангенсы от 75° до 90° и котангенсы от 0° до 15° записаны в таблице с точностью до 1’ угла.

Источник

Для чего нужна таблица брадиса

Советские инженеры уже ушли в прошлое. Теперь о них можно сочинять легенды. В общем, эти ребята достойны героических сказаний. Они построили крупную индустриальную страну, в которой дымили гигантские заводы, а вот ядерные реакторы, как раз, утечек не давали. По самым длинным в мире железным дорогам бежали поезда, самолёты и ракеты, во-первых, взлетали, а во-вторых, летали. И корабли воды бороздили. Что характерно, сделано это было за нищенскую зарплату и почти что вручную. В распоряжении советского инженера были нехитрые инструменты: карандаш, кульман, на нём ватман, рядом на столе – логарифмическая линейка, если повезёт, арифмометр «Феликс», а чаще всего, таблицы Брадиса.

Эти таблицы с дальнего расстояния выглядят каким-то волшебным артефактом, сэкономившим массу времени всем, кто занимался утомительными расчётами, неизбежными в любой инженерной работе. А Брадис, составивший волшебные эти таблицы, тоже выглядит волшебником, повелителем упрямых цифр.

Впрочем, волшебство здесь не при чём. Владимир Модестович Брадис (1890 – 1975) ведь был не колдуном, а был он математиком, придумавшим способ, который сократил трудоёмкость инженерных расчетов до минимума. Причём, сделал он это в начале 20-го века, задолго до того, как появились первые калькуляторы, которые, в конце концов, свели все расчётные сложности к нулю. Не говоря уже о компьютерах.

Компьютер-телефончик, маленький, но могучий, который, кажется, может всё, нынче находится у любого в кармане. Поэтому революционность изобретения Брадиса сейчас трудно объяснить. И всё же, что он сделал?

Для практических расчетов необходимо не так уж и много функций: квадраты и кубы, квадратные и кубические корни, обратная функция 1/x, а также тригонометрические функции (синусы, косинусы, тангенсы), экспонента и логарифмы. Брадис посчитал для этих функций все значения в широком интервале аргументов с определённым шагом и с приемлемой точностью. Приемлемой оказалась точность в четыре значащих цифры. Результаты расчётов были представлены в виде компактных таблиц и напечатаны, как небольшая по размеру брошюра. Название брошюры полностью отражало содержание: «Четырёхзначные математические таблицы». Эта брошюра в советское время переиздавалась едва ли не ежегодно и была очень востребована. Самое удивительное, что она до сих пор издаётся в России.Таблицы Брадиса имеют единообразную структуру для всех функций. В левом столбце и в верхней колонке каждой таблицы находятся значения аргументов находятся в левом столбце и в верхней колонке. В клетке, расположенной на пересечении столбца и колонки, находится соответствующее значение функции.

Но к чему длинные объяснения? Не лучше ли попробовать на примере? Давайте с помощью таблицы Брадиса рассчитаем значение какой-нибудь функции, например, синуса.

Откроем таблицу синусов и определим значение синуса для угла 10 градусов и 30 минут. Находим в левом столбце значение 10 градусов (11-я строка), а в верхней колонке – 30 минут (6-й столбец). На пересечении 11 строки и 6-го столбца, находим значение функции, 0.1822. Три последние столбца предназначены для уточнения значений минут. Дело в том, что в верхней колонке значения представлены только значения минут, кратные 6. Для определения синуса для других значений аргумента следует прибавить или вычесть поправку из ближайшего значения функции, представленного в таблице. Например, для угла 10 градусов и 32 минуты к уже найденному значению 0.1822 следует прибавить поправку из второго столбика, 6. Итак, синус 10 градусов 32 минут будет равен 0.1822+0.0006=0.1828.

Известно, что значения синуса и косинуса для определённого угла взаимосвязаны. Поэтому по таблице синусов можно определять и значения косинусов. Но аргумент для косинуса следует искать в правом столбце (четвертом справа) и в нижней строке. То же самое с тангенсом и котангенсом. Значения котангенсов ищем по таблице тангенсов аналогичным образом.

Итак, таблицы В. М. Брадиса позволяют определять четыре значащих цифры любой функции. Именно поэтому они называются «четырехзначными». Такой точности расчетов заведомо хватает для 90% инженерных расчетов. Кстати, когда рассчитывали траектории первых советских ракет, компьютеров ещё не было, а точности четырёхзначных таблиц было недостаточно. И пришлось таблицы Брадиса пересчитывать в восьмизначные.

Повторим ещё раз. Сейчас, когда калькуляторы встроены в мобильные телефоны, расчёты функций по таблицам Брадиса кажутся смешным пережитком прошлого. Впрочем, таким ли уж смешным, если в этом прошлом есть, чем гордиться? Большое ведь видится на расстоянии. А советские ракеты все-таки взлетали и летали.

Источник

Как пользоваться
таблицей Брадиса?

Давайте на нескольких примерах посмотрим как пользоваться таблицей Брадиса.

sin 7°=0.1219 косинусы смотрим снизу cos 82°=0.1392 надеюсь это понятно.
sin 3°42′=0.0645 на картинке красным цветом cos 80°24′=0.1668 то же просто

Хочу заметить все тоже самое верно и для определения значений
тангенсов и котангенсов.

Теперь возьмем более сложный вариант, если угол представленный в таблице отсутствует, то следует выбирать наиболее близкое к нему значение (из имеющегося в таблице синусов и косинусов), а на имеющуюся разницу, которая может быть 1′,2′,3′, взять поправочное значение из желтой графы, как показано в примере:
sin 3°45′=sin 3°42′+3′=0.0645+0.0009=0.0654 или
sin 3°45′=sin 3°48′−3′=0.0663−0.0009=0.0654

Так же необходимо запомнить правило, для синуса поправка имеет положительный знак, а для косинуса отрицательный
cos 80°27′=80°24′+3′=0.1668+(-0.0009)=0.1659 или
cos 80°27′=80°30′−3′=0.1650−(-0.0009)=0.1659

Оказывается пользоватся таблицей Брадиса не так уж и сложно. Надо еще раз очень внимательно все посмотреть, попробовать, и можно смело браться за самостоятельные расчеты.

Источник

Все о таблице Брадиса: синусы, косинусы, тангенсы, котангенсы

Что такое таблица Брадиса

Использование калькуляторов при сложных расчетах (например, формулах с применением логарифмов) сегодня считается стандартом по умолчанию. Но еще 20-30 лет назад, когда вычислительная техника была распространена не так сильно, на помощь приходили другие способы вычислений — с помощью специальных таблиц, логарифмической линейки или арифмометра.

Таблица Брадиса — математическое пособие, в котором собраны таблицы, необходимые для работы по курсу математики и для практических вычислений, созданное Владимиром Модестовичом Брадисом.

Свое название они получили от брошюры «Четырехзначные математические таблицы», составленной Владимиром Брадисом. Книга неоднократно переиздавалась в советское время большими тиражами (до 500 000 экземпляров) и широко использовалась в учебном процессе — на уроках алгебры, геометрии и физики.

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

Функциональные возможности таблицы

Самыми распространенными являются таблицы, содержащие тригонометрические функции (например, синус, косинус, тангенс, котангенс и арктангенс).

В целом, в сборнике Брадиса содержалось более 20 таблиц, в том числе, помогавшие найти значения:

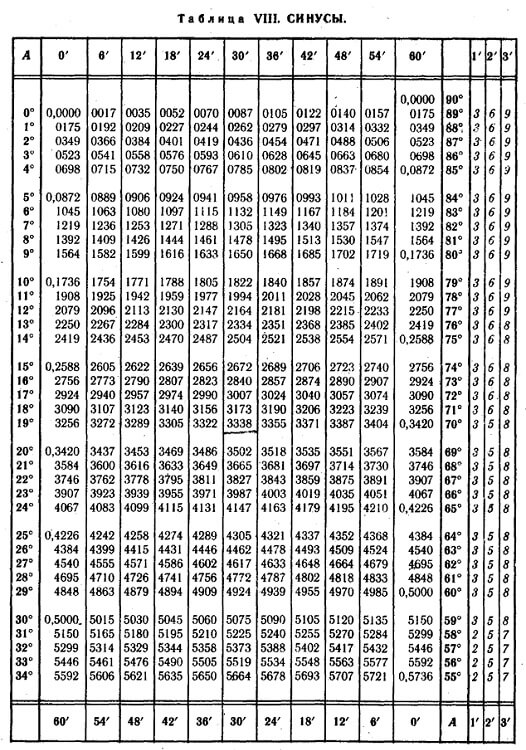
Таблица синусов и косинусов

В силу широкого использования синусов и косинусов в учебных задачах, это самая распространенная из таблиц Брадиса. Она дает значение этих тригонометрических функций для любого острого угла от 0° до 90°. С помощью дополнительных колонок можно находить и более точные спецификации. Это 6′, 12′,18, 24′, 30′, 36′, 42′, 48′ и 54′ для углов указанного диапазона, например:

Если нужны еще более точные показатели, то нужно использовать поправочные коэффициенты, отнимая и прибавляя их к ближайшему табличному значению минут. Используя их, находим:

Для нахождения косинусов можно использовать значения в правой колонке, но куда удобнее вычислять через синус угла, дополняющего до 90°. В этом случае:

Аналогично проводят и более точные вычисления, в том числе — с использованием поправочных коэффициентов:

Таблица для тангенсов и котангенсов

Аналогичным образом с помощью соответствующей таблицы Брадиса можно найти значения тангенса:

Для более точных показателей применяем поправочные коэффициенты (аналогично, как для таблиц синуса и косинуса):

С помощью правой колонки таблицы Брадиса со значением тангенсов можно найти котангенс. Альтернативный вариант — вычисление через тангенс угла, дополняющего искомый до 90°:

Важно отметить, что значения тангенсов (и соответствующих им котангенсов) распределены по двум таблицам:

Такое разделение связано с особенностями предоставления информации. Для котангенсов углов, близких к 90° (и котангенсам острых углов) проблематично использовать общие поправки, поэтому значения там даются индивидуально для каждого значения.

Например, в отдельных строках таблицы, без применения поправочных величин, приводятся:

Величину тангенса и котангенса можно узнать и имея в наличии только таблицу Брадиса по синусам и косинусам. Для этого надо воспользоваться формулами:

Подставляя необходимые значения получим:

Значения от 181 до 360 градусов

Таблицы Брадиса дают значения для углов от 0° до 90°. Остальные величины можно легко найти с помощью формул приведения. В этом случае угол, величину которого необходимо узнать, представляется как сумма (или разность) угла, кратного 90° и острого угла, например, для 140° это будет:

Формулы приведения, которые используются в этом случае, имеют вид:

Для примера можно провести расчет для ситуации, когда угол в 140° представлен как 90° + 50°:

Практические примеры использования таблицы

Таблицам Брадиса легко можно найти применение в современном учебном процессе, например, выполняя школьные уроки.

Задача №1

10-метровая лестница опирается на здание таким образом, что имеет угол наклона 35°. Необходимо узнать расстояние от земли до ее вершины.

Решение

Имеем треугольник, где угол BСA = 90°, BАC = 30°. По определению^

где ВС — высота лестницы, которую нужно найти, а АВ — известная из условия длина.

Узнав из таблицы Брадиса нужный синус и подставив все известные значения в формулу, можно найти ответ:

ВС (высота лестницы) = 10 м х 0,5736 = 5,736 метров.

Задача №2

Найдете длину тени от маяка высокой 30 м, если солнце находится в 60° над горизонтом.

Решение

Схематически условия задачи можно представить в виде треугольника, с прямым углом ВСА, и ВАС = 55°. По определению:

где АВ — высота маяка, а СВ — длина тени.

Определив по таблице Брадиса нужную величину и подставив в формулу все известные значения, получим:

СВ (длина тени) = 30 м / 1,732 = 17,32 метра.

Источник

КАК ПОЛЬЗОВАТЬСЯ ТАБЛИЦЕЙ БРАДИСА ПРИМЕРЫ

Как пользоваться таблицей Брадиса инструкция с примерами

Каждая таблица Брадиса дает значения какой-либо величины (функции) в зависимости от значения некоторой другой величины (аргумента). На­пример, таблица 3 дает значения квадрата в зависимости от значений возводимого в квадрат числа (функция у = х 2 аргумента х), таблица 7 — значения площади круга в зависимости от значений его диаметра (функция К = πd 2 /4 аргумента d) и т. д. Ради экономии места все таблицы сборника расположены «в два хода»: каждое табличное значение функции находится на пересечении строки, имеющей в заголовке (слева) некоторые первые цифры соответствующего назначения аргумента, и столбца, имею­щего в заголовке (сверху) остальные его цифры. Например, для квадрата числа 5,67 находим в таблице 3 на строке 5,6 в столбце 7 значение 32,15, представляющее со­бой результат округления до 4 значащих цифр точного квадрата 5,67 2 = 32,1489.

Каждая таблица содержит значения функции не для всех, а лишь для некоторых значений аргумента. Возникает вопрос: как получить значения функции для проме­жуточных значений аргумента? Операция получения таких значений носит название «интерполяции». Ее иногда образно называют «чтением между строками таблицы».

В случае таблицы с равномерным или почти равномерным изменением функции применяется так называемая «линейная интерполяция», состоящая в следующем. Ес­ли при увеличении значения аргумента на И единиц какого-либо разряда функция увеличивается на d единиц некоторого разряда, то в силу равномерности изменения функции увеличение аргумента на 1 вызывает увеличение функции на d/h единиц, а увеличение аргумента на u — увеличение функции на v = du/h единиц. Очевидно, что для получения искомого значения функции надо взять ближайшее меньшее таблич­ное ее значение и прибавить эту «поправку» v. Например, чтобы узнать, чему равен квадрат числа 8,053, берем в таблице 3 8,05 2 = 64,80, 8,06 2 = 64,96, 8,07 2 = 65,12 и убеждаемся, что изменение функции здесь почти равномерно: при ступени h = 0,01 или 10 тысячным табличная разность составляет здесь 16 сотых. Данное значение ар­гумента 8,053 превосходит ближайшее меньшее табличное его значение 8,05 на u = 3 (тысячным), а потому поправка v равна 16·3/10 = 4,8 = 5 (сотым). Прибавив ее к бли­жайшему меньшему табличному значению функции 8,05 2 = 64,80, получим 8,053 2 = = 64,80 + 0,05 = 64,85 (непосредственное умножение дает точно 8,053 2 = 64,850809).

Вместо того чтобы брать поправку на «избыток» данного значения аргумента над ближайшим меньшим табличным его значением, как мы это только что делали, мож­но дать поправку на его «недостаток» по сравнению с ближайшим большим таблич­ным его значением и вычитать поправку из ближайшего большего значения функ­ции. Например, для получения квадрата числа 8,057 берем 8,06 2 = 8,060 2 = 64,96 и вы­читаем поправку на 3 тысячных, равную 5 сотым, получая 8,057 2 = 64,91 (при точном значении, равном 64,915249). Поправка на избыток выгоднее, если избыток не пре­восходит половины ступени; в противном случае выгоднее брать поправку на недо­статок.

Операцию линейной интерполяции можно объяснять, исходя не из равномер­ности изменения функции, как мы это сейчас делали, а из пропорциональности при­ращений аргумента и функции, т. е. из пропорциональности избытка аргумента и по­правки для функции, прекрасно иллюстрируемой на графике, где получаются два по­добных прямоугольных треугольника, один с катетами h и d, другой с катетами u и v. По существу, оба способа, конечно, тождественны, так как оба основаны на одной и той же пропорции u:v=h:d.

Какова точность результатов, получаемых посредством линейной интерполяции? Здесь имеются три источника погрешностей: неточность взятого ближайшего таблич­ного значения функции, не превосходящая половины единицы разряда последней его цифры; неточность поправки, обусловленная неточностями табличных значений и округлением поправки, и, наконец, неточность поправки, вызванная неполной равномерностью изменения функции. Более глубокое рассмотрение вопроса показы­вает, что при разнице двух соседних значений табличной разности, не превосходящей 4 единиц, третий источник погрешности сколько-нибудь заметного влияния не име­ет, и общая погрешность результата линейной интерполяции лишь в исключительно редких случаях может немного превзойти единицу разряда последней цифры. Это за­ключение легко проверяется на опыте. Например, пользуясь таблицей квадратов, нахо­дим, применяя линейную интерполяцию, квадраты чисел, приведенных ниже в пер­вой строке, и пишем их во второй строке, а в третьей строке помещаем соответствую­щие точные квадраты, округленные до четвертого десятичного знака, в четвертой же — разности чисел второй и третьей строк, выраженные в сотых долях.

Как видим, погрешности интерполированных значений нигде не превосходят единицы разряда последней цифры.

Именно эти числа и приведены на строке 8,0 таблицы квадратов справа (набраны курсивом). Как показывает опыт, применение этих готовых поправок сберегает до 50% времени, затрачиваемого на работу с таблицами.

Если табличные разности на протяжении строки меняются более заметно, гото­вые поправки приходится вычислять для частей строки, как это сделано, например, в таблице 9 для строк 73°, 74°, 75° или для нескольких первых строк таблицы мантисс логарифмов. Если изменение табличных разностей на протя­жении строки выражено еще резче, от готовых поправок приходится отказаться. В та­ких случаях операцию линейной интерполяции приходится проводить полностью, находя h, d, u, v = du/h, как, например, в таблице 15 и нескольких других.

Как мы уже видели, если избыток данного значения аргумента больше половины ступени, выгоднее пользоваться ближайшим большим значением функции, отнимая от него поправку на недостаток данного значения аргумента по сравнению с ближай­шим большим его значением. Поэтому во всех таблицах, где аргументом служит угол и где ступень равна 6′, готовые поправки даны только на 1′, 2′, 3′. Если избыток со­ставляет 4′ или 5′, надо брать поправку на 2′ или 1′, вычитая ее из ближайшего боль­шего значения функции. Кроме экономии места, занимаемого таблицей, это дает не­который выигрыш в точности получаемых результатов, так как малые поправки точнее больших.

Необходимо решительно предостеречь от применения линейной интерполяции в случае резко неравномерного изменения функции. Всякий раз, когда готовые по­правки не даны, а нужно интерполировать, следует выяснить, насколько равномерен ход функции, и применять линейную интерполяцию лишь в том случае, когда со­седние табличные разности мало отличаются друг от друга (не больше чем на 4 единицы), а в противном случае искать других путей. Так, например, желая найти lg sin 1°04’36», берем в таблице 15, где готовых поправок нет, lg sin 1°04′ — 2,2699, lg sin 1°05′ = 2,2766, lg sin 1°06′ = 2,2832 и убеждаемся, что линейная интерполяция здесь допустима, так как табличные разности равны 67 и 66. Вычисляя v = 67·36/60 = 40,2 = 40 и прибавляя эту поправку к табличному логарифму 2,2699, получаем lg sin 1°04’36» = 2,2739 (по семизначным таблицам получается 2,2739331). Но если на­до получить lg sin 0°05’30» и мы применим тот же способ линейной интерполяции, то получим lg sin 0°05′ = 3,1627, d = 792, h =60″, u = 30″, v = 792/60 · 30 = 396, lg sin 0°05’30» =60= 3,2023, в то время как более точное значение этого логарифма, найденное по семи­значным таблицам, есть 3,2040886. Недопустимо большая погрешность нашего ре­зультата обусловлена резко неравномерным изменением функции: рядом с использо­ванной нами табличной разностью 792 находится разность 669, линейная интерполя­ция здесь недопустима. Здесь можно воспользоваться тем обстоятельством, что при очень малых углах синус весьма мало отличается от радианной меры (меньше чем на шестую часть куба этой радианной меры). В таблице 11 берем радианную меру уг­ла в 5′, равную 0,0014544, а также угла в 30″, равную 0,00014544, и, складывая, получа­ем число 0,0015998, представляющее собой приближенное значение sin 0°05’30» с 7 точными десятичными знаками. Найдя по таблице 13 его логарифм, получаем 3,2041, т. е. как раз то, что надо.

Во многих случаях таблицы дают непосредственно значения функции лишь в од­ном ограниченном интервале значений аргумента, но путем несложных дополни­тельных расчетов, производимых обычно в уме, можно существенно расширить этот интервал. Так обстоит дело с таблицами квадратов, кубов, обратных значений и ряда других. Возьмем, например, таблицу 7, дающую непосредственно значения площа­ди круга с диаметром от d = 1 до d = 10, замечая, что при увеличении диаметра круга в 10 раз его площадь увеличивается в 10 2 = 100 раз, мы можем по этой же таблице нахо­дить площадь круга любого диаметра. Например, желая найти площадь круга диа­метра d = 49,52, находим по таблице сперва площадь круга диаметра 4,952 (стро­ка 49, столбец 5, поправка на 2), равную 19,26, а затем увеличиваем этот результат в 100 раз и получаем окончательно 1926. Чтобы найти площадь круга с диаметром d = 0,04567, получаем сперва площадь круга диаметра 4,567 (строка 45, столбец 7, вычитается поправка на 3), равную 16,38, потом уменьшаем ее в 100 2 = 10000 раз и получаем 0,001638.

Разобрав во всех деталях вопрос о разыскании посредством таблиц значения функции по данному значению ее аргумента, то есть так называемый «прямой воп­рос», переходим к «обратному вопросу», когда по данному значению той функции, для которой таблица составлена, надо найти соответствующее значение аргумента.

Вопрос о точности, с какой обратная линейная интерполяция дает искомое зна­чение функции, довольно сложен. Оказывается, что здесь возможны самые различ­ные случаи и что результат здесь тем более точен, чем больше табличная разность (предполагается, что линейная интерполяция допустима). Например, если дано при­ближенное значение sin А = 0,9997 с 4 точными десятичными знаками, то в таблице 8 мы находим целых три угла с таким синусом (88°30′, 88°36′, 88°42′). Полагая А = 88°36′, надо иметь в виду, что это значение искомого угла весьма неточно: оно мо­жет отличаться от точного до 9′. Если же sin A = 0,1070, то находимое по таблице 8 с помощью готовых поправок значение 6°08′ отличается от точного, как можно пока­зать, не больше чем на 1′: применение способа границ приводит к заключению, что 6°08′ Поделитесь ссылкой с друзьями:

Источник