для чего нужно интегрирование

19.05.202320.05.2023 admin 0 Comments

Сегодня вы поймёте, что такое интеграл в математике

(и в программировании)

Недавно мы разобрали, что такое знаки Σ и П в математике — это операции, которые, по сути, похожи на циклы в программировании. В одном случае мы складывали много чисел по определённому принципу, а в другом — умножали.

Сегодня посмотрим на интеграл ∫ — что это такое и какой цикл можно сделать из него.

Но сначала: что такое функция

Интегралы в математике всегда связаны с функциями, поэтому сначала поговорим про них.

Функцию можно представить как «коробку с математикой». У тебя есть какая-то масса математических операций, ты их «запаковываешь» в функцию. Теперь ты можешь эту массу операций вызывать в своих математических выражениях одним действием.

У функции есть один или несколько аргументов — это те числа, к которым нужно применить массу математических операций. Можно представим, что мы засунули это число в коробку с математикой, потрясли и получили на выходе другое число.

Если посчитать f(x) для одного числа, получится другое число. Если посчитать f(x) от 100 чисел, получится 100 других чисел. А если непрерывно считать f(x) для бесконечного количества чисел, то получится бесконечное количество других чисел.

Что такое интеграл

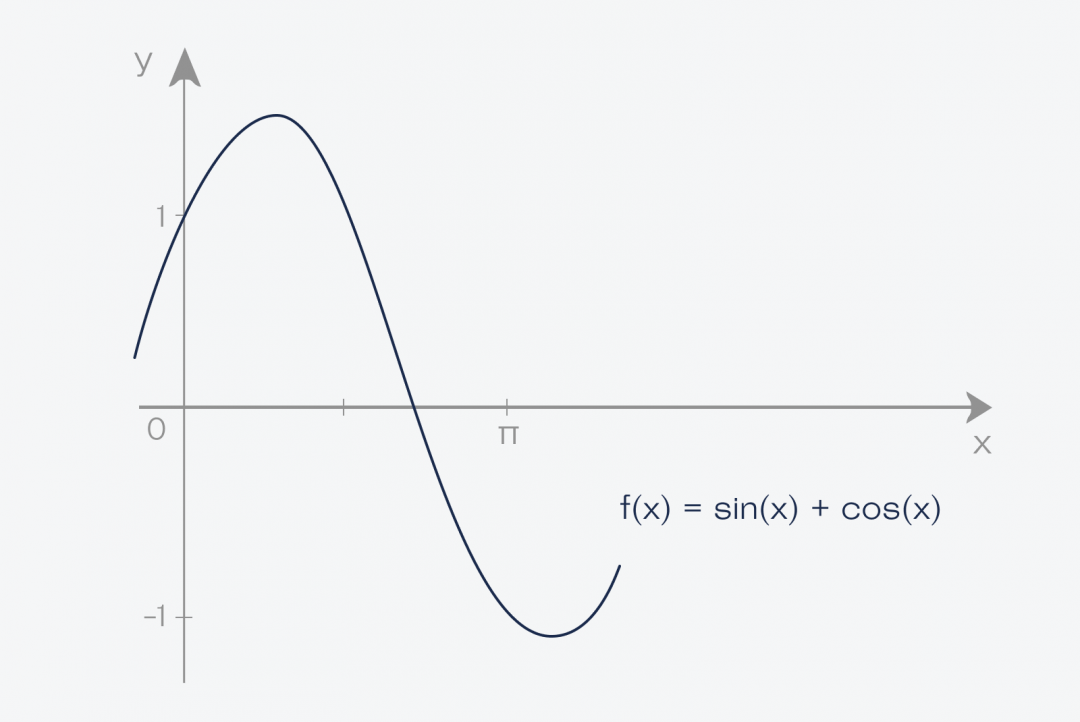
Итак, у нас есть некая функция, у неё есть числа на входе и числа на выходе. Эти пары чисел можно использовать для построения графика функции.

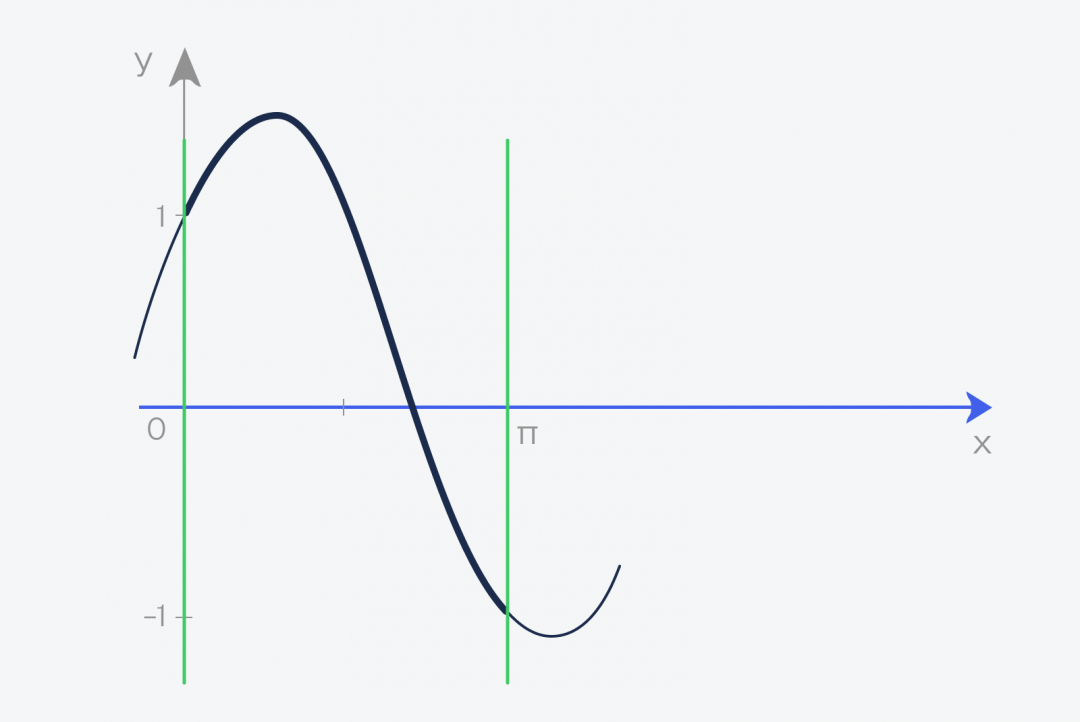
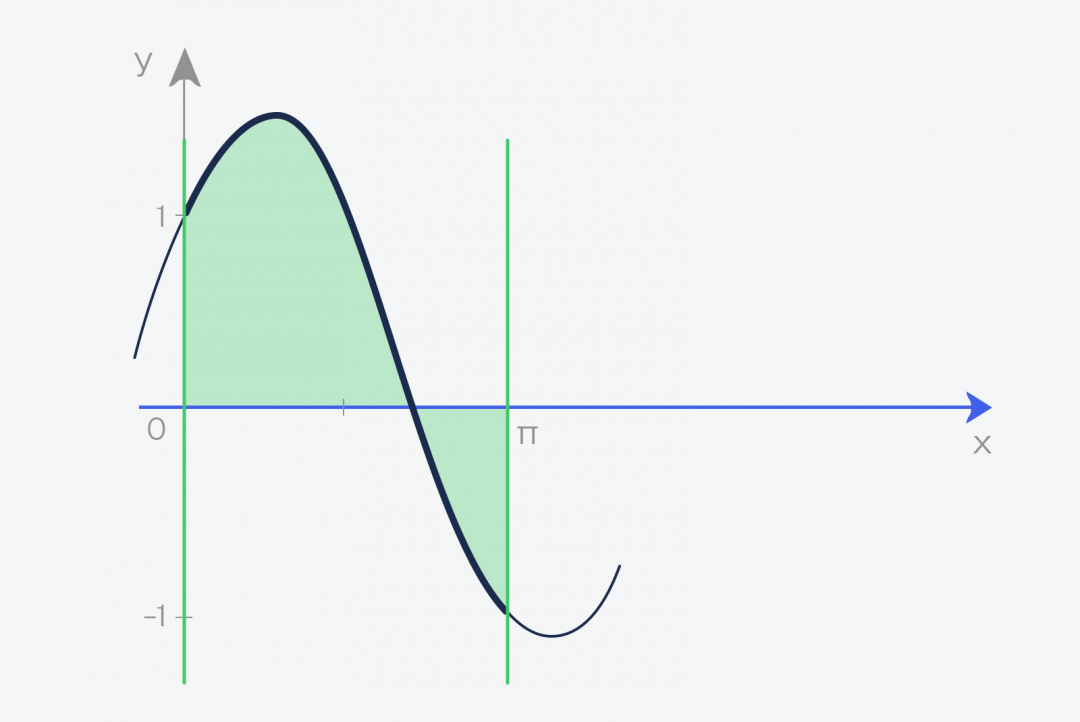
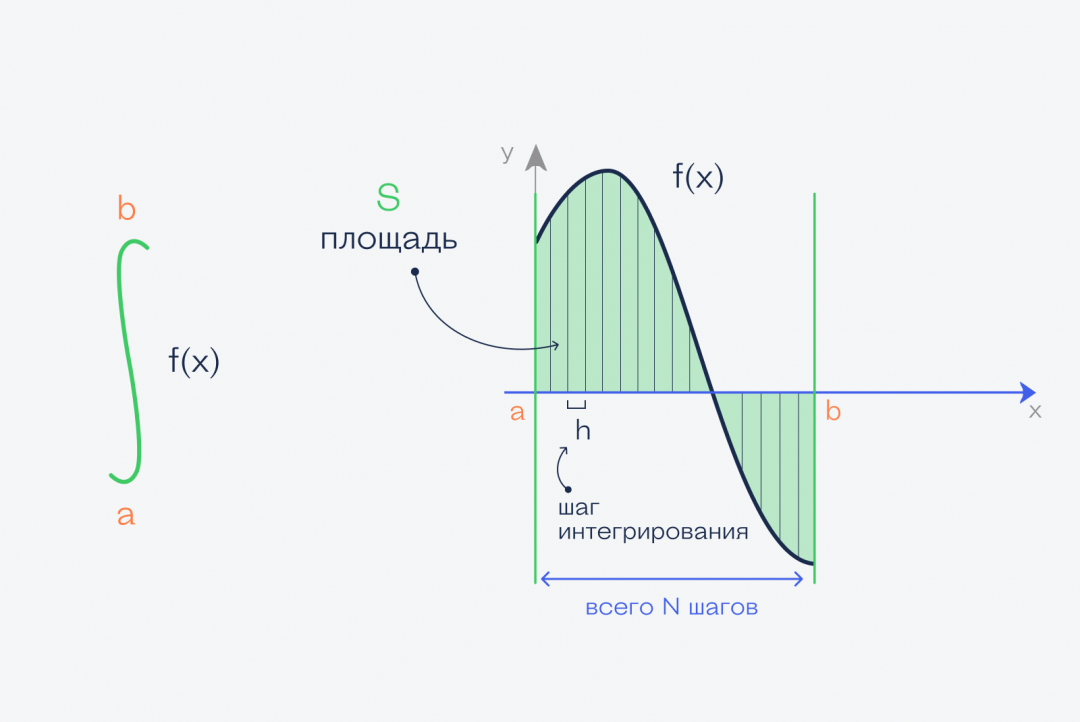
Теперь берём этот график функции и проводим две линии, которые ограничивают график. Получается фигура, которая сверху зависит от нашей функции, а с остальных сторон ограничена прямыми линиями и осью:

А теперь то, ради чего всё это затевалось:

✅ Площадь этой фигуры и есть интеграл функции f(x) = sin(x) + cos(x) на отрезке от a до b

В нашем случае мы считаем интеграл от нуля до числа пи — 3,1415926.

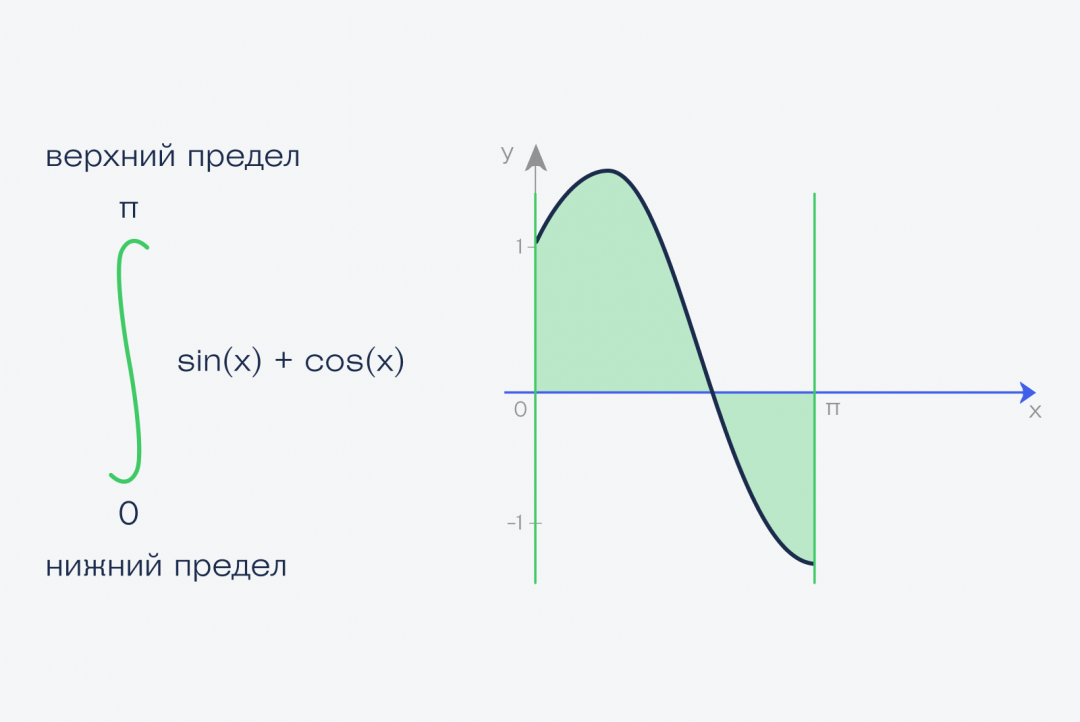
Это называется определённый интеграл. Определённый — это когда у нас определены начало и конец фигуры — в математике это называют пределами интегрирования. Записывается этот интеграл так:

В математике есть ещё неопределённые интегралы, у которых нет пределов интегрирования. Ими мы заниматься не будем, потому что ответом к неопределённому интегралу будет не конкретное число, а формула.

Зачем нужны интегралы в народном хозяйстве

Вы удивитесь, но в первую очередь интегралы нужны, чтобы находить площади и объёмы. В буквальном смысле: вот фигура, вот её описание в виде функции, проинтегрировали — узнали площадь. Будете, например, заливать бетоном красивую кривую дорожку — узнаете, сколько вам нужно бетона.

Интегралы нужны в математике и физике, это один из инструментов вычислений.

Если вы астрофизик, интеграл поможет вам рассчитать какие-нибудь свойства звёзд с течением времени. А математики говорят, что в интегралах не нужно искать практический смысл; их нужно любить, как мать, и почитать, как отца.

Как посчитать интеграл (то есть найти площадь)

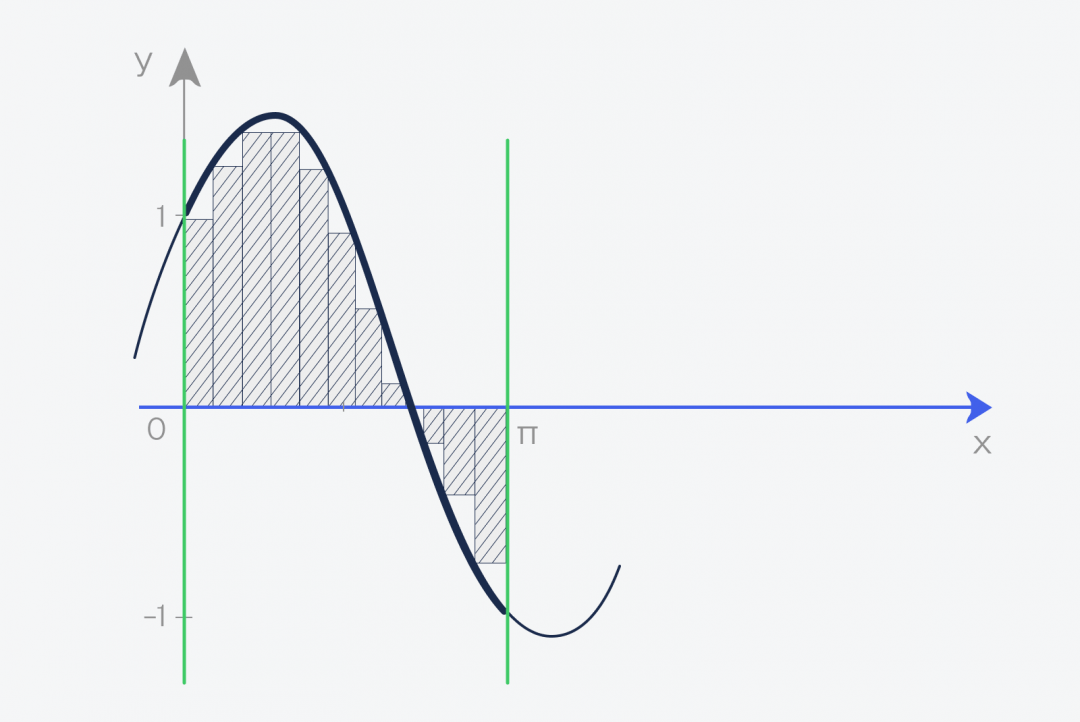
Если бы у нас был прямоугольник, то всё просто: перемножаем высоту на ширину. Если бы была трапеция, тоже ещё как-то что-то можно. Но сверху у нас кривая, поэтому так сделать не получится. Решение придумали такое:

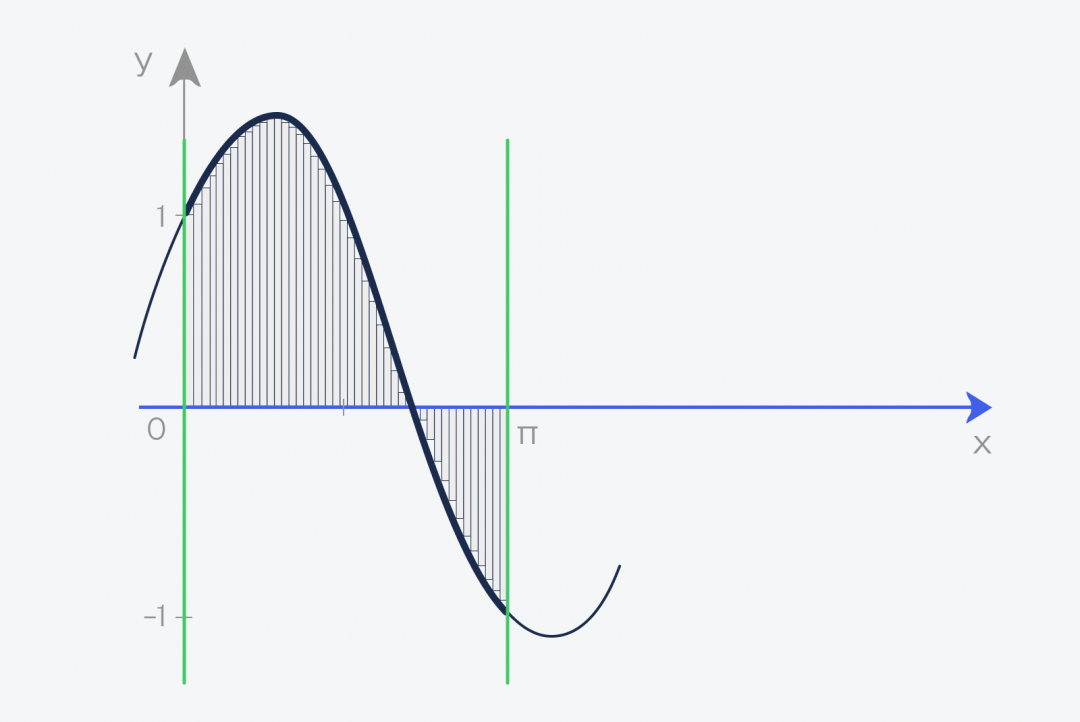
Минус такого подхода в том, что, как бы мы ни старались, прямоугольники не могут повторить все изгибы, и появится погрешность. С другой стороны, чем тоньше будут эти прямоугольники, тем точнее будет ответ. Получается, что наша задача — нарезать фигуру как можно тоньше.

Теперь задача становится намного проще: мы просто считаем площадь каждого прямоугольника и складываем их вместе. В таком виде задачу уже можно решить простым алгоритмом.

Пишем код

Раз нам нужно разбить интервал на много частей а потом с каждой из них сделать одно и то же, то это точно задача для цикла. Для этого нам понадобится шаг цикла — какой ширины будут наши прямоугольники, чтобы бы могли их одинаково перебирать.

Чтобы посчитать шаг, находим расстояние между конечной и начальной точкой и делим на желаемое количество прямоугольников (это будет нашей точностью интегрирования).

Общая логика работы будет такая:

На картинке — все исходные данные, а ниже — код, который считает интеграл. Смотрите на картинку и читайте комментарии: так будет ещё проще разобраться в коде:

Что дальше

Теперь этот код можно изменить так, чтобы он считал интеграл в любых пределах у любой функции. С точки зрения математики это не самый точный результат, но всё зависит от того, сколько точных знаков после запятой нам нужно.

В следующей серии продолжим разбираться со страшной математикой. Если есть пожелания для разбора — напишите в комментариях.

Источник

Интеграл простыми словами

Интегралы начинают изучать еще в школе. Но никто из учителей не говорит, зачем это нужно, как использовать эти знания в жизни. Мало кто вообще способен объяснить простыми словами, что такое интеграл, даже в университете. А мы попробуем.

Простыми словами…

Если коротко — интеграл, это сумма маленьких частей. Да, точно так же как и сложение 2+2, только части бесконечно маленькие, естественно и количество их — бесконечно.

Знак интеграла ∫ — это вытянутая буква s (длинная «эс» существовала до начала 19-ого века писалась так — ſ). Первая буква слова summa.

Интегрирование — это сложение бесконечного количества частей бесконечно маленького значения.

Почему обычного «плюсования» не достаточно? Просто в алгебре нет никаких бесконечно малых или больших.

Бесконечно малая величина, это не какое-то конкретное число. Это абстракция, в реальном мире аналогов просто нет. Мы придумали так для удобства. Что-то настолько маленькое, что измерять его бессмысленно, но в расчетах использовать можно.

Слово «интеграл» происходит от латинского integer, что означает «целый». Даже в названии есть намек некое действие, что-то вроде восстановления чего-то целого.

Лучше всего показать «на пальцах», точнее на примере. Предположим, мы хотим узнать площадь фигуры как на картинке (она называется криволинейная трапеция, потому, что одна из сторон создана кривой линией). Зачем нам это нужно? Например, это часть крыла самолета и нужно знать его площадь.

Можно, конечно, разбить фигуру на две, прямоугольник и треугольник.

Но останется «пробел», площадь которого будет неизвестна. Чтобы увеличить точность, можно разделять на большее количество фигур, но все равно будет оставаться какая-то, пусть и небольшая, но «не закрашенная» область. Фигуры будут становиться все меньше и меньше… Очевидно, что процесс измельчения будет бесконечным, по крайней мере в воображении.

Но, в реальности, бесконечный процесс попросту не нужен. На самом деле вычислить такие вещи как площадь круга, длину диагонали квадрата или объем пирамиды невозможно, значение будет бесконечным, естественно, практического смысла бесконечные числа не имеют и мы их «округляем» до нужного предела точности — приблизительно.

Такой метод в Древней Греции назывался «исчерпание». Аналогия с водой тут очень уместна, если представить, что черпаешь из ведра при помощи кружки, то сначала кружки будут полные, но чем ближе ко дну, тем меньший объем будет попадать в кружку. Первой известной личностью «взявшей интеграл» был Архимед, он фактически решил задачу по нахождению площади круга и площади параболы ничего не зная ни про пределы, но даже про число «пи».

Чем больше будет фигур, тем больше будет и точность расчета и тем меньше будут сами фигурки. Если площадь маленьких фигурок будет бесконечно малой, то есть стремится к нулю (но не равняться ему), сумма всех этих площадей будет равна сумме большой фигуры с бесконечно большой точностью.

То же самое происходит при интегрировании:

Фигура на картинке разбивается на столбцы бесконечно маленькой ширины. Ширина у нас Х. Бесконечно малое число обозначается d. То есть dx — это бесконечно малый «икс».

Сложение бесконечного числа частей бесконечно маленького размера это и есть интегрирование.

Чтобы узнать площадь фигуры нужна еще высота, а это y. Высота везде не одинаковая, она постоянно меняется. И мы знаем как именно! Ведь кривая может быть (а может и не быть, но в нашем случае так и есть) функцией y=f(x), то есть значение у меняется по закону (буква f об этом говорит) зависимому от х. Поэтому «эф от икс». Значит высота это f(x). Функция, кстати, тоже бесконечная.

Высота конкретного прямоугольничка, это значение функции в этой конкретной точке (почему точке, потому, что ширина полоски у нас бесконечно маленькая, мы так договорились в самом начале).

Площадь, это высота умноженная на ширину. За высоту можем брать и y и f(x), они равны. За ширину у нас играет dx. Итак, момент истины:

f(x)dx — площадь нашего маленького столбика. В если собрать из все вместе, будет сумма бесконечно маленьких столбиков.

А площадь нужна не бесконечной фигуры, а той что начинается от 1 и закачивается на 5. Если написать эти цифры над и под значком интеграла, получится определенный интеграл.

Собственно и все, интеграл — это сумма бесконечно малых приращений (то есть значений) какой-то функции. Не сложно и не страшно, если не усложнять.

Что мы делаем? Разрезаем фигуру на «ленточки» изменяем площадь этих ленточек и собираем все обратно (суммируем).

Интересно, везде идет речь о сумме, а площадь считается умножением. Парадокс? Нет, умножение это ведь то же самое, что и сложение: 2+2+2+2=2*4. То же самое происходит и с площадью. Чтобы выяснить какова площадь прямоугольника со сторонами 5 и 4, перемножаем 5 на 4, или разделяем прямоугольник на 5 полосок шириной в «единицу» и складываем 4+4+4+4+4=5*4=20.

Никакого противоречия здесь нет. Вот только умножение работает в случае одинаковых величин, простых фигур или прямолинейного движения без ускорения. В остальных случаях — интегрирование.

Зачем нужен интеграл

Из примера выше уже понято, что одна из полезных задач интегрирования — это расчет площади криволинейных фигур. В любой сложной ситуации, если сложность эта заключается криволинейности или неравномерности мы используем интеграл.

Но лучший способ объяснить, что такое интеграл простыми словами — показать еще пару примеров. Как когда-то в детстве объяснили сложение на яблоках. Для чего интеграл может понадобиться?

Предположим, нужно построить храм кому-то из древнегреческих богов, такой чтобы место в нем хватило всем, крыша была прямоугольной, а колоны круглыми, ведь так красивее (а еще прочнее).

Давление колонны на фундамент легко посчитать, если она квадратного сечения, делим силу на площадь и вуаля. А если колонна круглого сечения? Какова площадь круга?

Можно конечно, не напрягаться, и заменить круг эквивалентным квадратом (квадратура круга), но каким? На всякий случай побольше, чтобы наверняка ничего не развалилось. Но это не наш метод, особенно, если ни бесконечного числа рабочих, ни бесконечного числа мрамора в действительности нет и взять негде, а казнить за неэффективное использование бюджета никто не запрещает.

Прием с эквивалентом площади на самом деле простой, использовался древними людьми. Очень-очень древние греки ничего не знали об интегрировании, а Архимед еще не родился, тем не менее, чтобы рассчитать площадь круга, в него выкладывались камешки. Когда круг заполнялся, камешки собирались и раскладывались в виде квадрата. Чем меньше камешки тем… Ничего не напоминает?

Еще примеры из жизни

Конечно, в физике интеграл «берут» постоянно. Вместо Х, может быть время, и тогда мы будем иметь дело с функцией времени, такой, например, как скорость. Ускорение — это скорость изменения скорости. Скорость, это скорость изменения координат. Пробежавшись от ускорения к скорости мы уже дважды использовали интеграл.

В обратную сторону: первая производная пути, это скорость, вторая производная — ускорение. Если ускорение равно нулю, значит скорость не менялась.

Интегрирование и дифференцирование, такие же «парочка» как и умножение и деление, суммирование и вычитание, только не с цифрами, а с функциями. Это взаимно-обратные операции. В случае производной, мы не «складываем», а «отнимаем».

Если проинтегрировав функцию изменения скорости (ускорение) получим константу (число, например, 60, а не формулу y=2x), значит, скорость не изменялась со временем, ускорения не было. Если, взяв приводную (дифференциал) функции скорости по времени, получим ноль — скорость не менялась, ускорение равно нулю.

То есть, имея в своем распоряжении какую-то функцию (зависимость чего-то от чего-то), мы можем ее дифференцировать или интегрировать. Точно также как если бы умножали и или, вычитали и складывали обычные числа.

Например, у нас есть функция изменения координат от времени. В реальном мире мы вышли на пробежку. Бежал наш виртуальный спортсмен 30 минут, первые 10 минут очень быстро, вторые 10 минут уже с одышкой, ну а последние 10 прошел пешком.

Очевидно, что координаты бегуна в начале и в конце разные (он же не стоял на месте). Если координаты менялись — скорость не равнялась нулю.

Скорость не была одинаковой, а менялась в зависимости от времени (больше времени, больше усталость, меньше скорость).

Итак, у нас есть функция изменения координат. Первая производная даст нам новую функцию — изменения координат, вторая производная — функцию ускорения. И первая и вторая функции зависят от одной и той же переменной — времени.

Еще один пример, вычисление массы. Масса, это произведение плотности на объем. Если плотность и объем одинаковы (это стакан воды) никаких проблем нет. А если плотность меняется (тот же стакан, только с коктейлем в несколько слоев)? В таком случае нужно знать закон (зависимость с которой изменяться плотность жидкости в стакане).

Если вам такие примеры не близки, то представьте себе, что взяли кредит под сложный процент. Тогда ваш долг будет расти не линейно. И вы будете интегрировать…

Если нужно узнать какую работу нужно затратить на перемещение предмета не по прямой, а если, нужно рассчитать лучшую цену, зная зависимость спроса от предложения, а если нужно посчитать за какое время рабочие выкопают яму, если это не роботы, а живые люди, которые устают со временем, а если…

Если посмотреть вокруг, не найдется в реальном мире ни идеальных фигур, ни ровных графиков, ни равномерного движения без ускорения, ни линейных зависимостей в поведении человека «разумного».

Все эти простые штуки из науки, просто частные случаи. А значит, в реальном мире интеграл более полезен, чем кажется. Конечно, кривые сложнее прямых и именно поэтому всю свою историю люди упрощали себе жизнь: делили поле прямыми, на квадраты и прямоугольники при помощи натянутой веревки. Считали среднюю скорость, а не мгновенную в каждой точке маршрута, полагали, что тело прошенное под углом к горизонту летит по параболе, а не баллистической кривой… Но, просто — не значит точно.

Говоря простым языком, интегрирование — это такой же инструмент, как и суммирование, в нем нет никаких особых тайн и сложностей. Кроме одной — представить себе бесконечность сложнее, чем натуральные числа, у которых есть наглядные представления в природе. Но справляемся же мы как-то с представлениями таких абстракций как «ноль» или «отрицательное число». С матанализом просто нужно чуть больше воображения.

Ну а если уж совсем просто, для гуманитариев, то производная винограда — это вино. Интеграл вина — это виноград.

Источник

Так зачем же всё-таки нужны интегралы?

Ответ на вопрос, интересующий всех еще со школы.

Можно найти примеры применения математических законов в разных сферах человеческой жизнедеятельности. Я хотел бы попытаться объяснить интегрирование через воду, а точнее через измерение и мониторинг ее качества. Для начала нужно разобраться что такое общий органический углерод и как он связан с качеством воды. Общий органический углерод выражает, в виде концентрации, содержание всех органических соединений в воде. Он является важнейшим индикатором чистоты. Допустимые концентрации закреплены законодательно, а воду с высоким содержанием органических соединений запрещено сбрасывать в водоемы.

Что представляют из себя эти соединения и почему так важно знать их концентрацию? Органикой считаются вещества, содержащие углерод (С). Бытовым примером являются продукты питания. Также можно упомянуть природные источники. Например, если после сбора картошки промыть ее водой, то количество органических соединений в воде увеличится.

Концентрации, если мы говорим о производстве, необходимо знать для того, чтобы не получить штраф за сброс загрязненной воды в реку или озеро. Если смотреть глобальнее, то для разработки системы очистки воды необходимо провести количественный и качественный анализы. Говоря иначе, понимать, что в ней содержится и в каком количестве.

Поговорим, о массовом производстве картофеля. Его выращивают, собирают, промывают от земли, сортируют и упаковывают. После промывки воду нельзя просто так слить в водоем, так как она загрязнена, ее нужно сначала очистить.

Для сохранения водоемов нужно очищать воду, а чтобы ее правильно очищать, нужно знать сколько в ней органических соединений. Итак, как это измерить и, при чем тут интеграл?

Измерение можно провести с помощью специального прибора для мониторинга качества воды. Прибор берет пробу воды, за несколько минут проводит измерение и, вот, уже известна концентрация. Ниже представлено само устройство.

Без интегрирования прибор не смог бы определить степень загрязненности воды и, возможно, водоемы бы гибли один за другим. Для того, чтобы докопаться до истины, нам придется углубиться в прибор и понять, по какому принципу строится измерение.

При окислении углерода (С) образуется углекислый газ (СО2). Окисление в данном случае можно заменить на горение или сжигание. Если сжечь С, получим СО2. Реакция выглядит следующим образом:

Это ключевой момент. Если сжечь ту воду, которая осталась после промывки картофеля, то получим углекислый газ и пар. Именно это и делает устройство. Прибор знает зависимость концентрации органических веществ в воде от количества углекислого газа, выделяемого при их сжигании. Зависимость линейна и может быть определена путем одного контрольного измерения. Cпециалист, работающий с устройством, готовит раствор с заранее известной концентрацией органических веществ, затем сжигает его в приборе, и далее прибор строит линейную зависимость С от СО2, которая впоследствии берется за основу. Упрощенно говоря, измерение строится от обратного. Первоначально необходимо измерить сколько СО2 выделится при известном количестве С, чтобы потом измерять неизвестные концентрации С. Как уже упоминалось выше, зависимость линейна, соответственно, чем больше органических веществ содержится в воде, тем больше углекислого газа выделится при ее сжигании.

Забирается вода с помощью специальной роботизированной системы. По сути, это шприц со стальной иглой, двигающийся по горизонтальной оси. Он перемещается до сосуда с пробой, опускается, забирает небольшой объем, потом поднимается и направляется к печи. Далее впрыскивает пробу в печь. Проба сжигается при температуре 1200 градусов Цельсия. Прибор измеряет количество выделенного углекислого газа, а затем, по заранее определенной зависимости, сопоставляет какой концентрации соответствует выделенное количество газа.

Теперь необходимо отправиться на последний уровень. Проблема интеграла в том, что он всегда где-то глубоко. Лежит не на поверхности. Но мы уже близко. Остался финальный рывок.

Итак, что значит измерить количество углекислого газа? В каких единицах измерения это количество выражено? Как оно выглядит в реальном времени? Начнем с последнего, выглядит оно, следующим образом:

По оси У, обозначен диапазон охвата прибора от 0 до 100 процентов, где 100 процентов — это максимальное количество углекислого газа, которое может быть измерено. По оси Х, обозначено время. Кривая начинает идти вверх при измерении первых молекул углекислого газа.

Предположим, что вы сидите за компьютером, а кто-то готовит вам пасту на кухне. Вдруг в пасту добавляется красное вино. Сидя за компьютером, вы сначала слегка чувствуете запах вина, потом до вас доходит кульминационная часть, далее запах начинает потихоньку пропадать, в итоге вы уже совсем не чувствуете, что в пасту когда-то было добавлено вино.

Заменим запах вина на углекислый газ и получим понимание графика выше. Сначала прибор измеряет первые молекулы углекислого газа, потом основную часть и далее остаточные частички.

А как посчитать площадь кривой, образованной процессом, описанным выше? Ответ, прост: интегрированием. Так как фигура на графике значительно сложнее прямоугольника, интеграл необходим для расчета площади под кривой. В моем примере эта кривая образована сжиганием воды с органическими соединениями. Процесс выделения углекислого газа, образованного при сжигании, описан математически и изображен графически. Единицы измерения в данном случае — это проценты помноженные на время (%*с)

Возможно, математика – это не самая захватывающая наука по сравнению с физикой, химией, механикой или электротехникой. Можно рассматривать химические реакции и вещества, образованные в результате этих реакций, проектировать приборы и программировать роботизированные системы, но все это было бы проблематично, не имей мы некую сухую точу отсчета. Математика – это средство описания мира вокруг нас, она помогает изложить интересные процессы на бумаге, в краткой и сухой форме, а также выразить некие сложные величины в количественном виде.

Вполне вероятно, что без интегралов, вода, которую мы пьем, была бы не пригодна к употреблению. Так проникнемся же к ним уважением.

Источник

Интуитивное объяснение интеграла. Часть I — от умножения натуральных чисел до Ньютона и Лейбница

0. Предисловие

Математика представляет собой универсальный, мощный и элегантный раздел знания. По-сути её предмет и значение невозможно разделить с наиболее фундаментальными разделами философии — логикой, онтологией и теорией познания. Именно поэтому она касается прямо или косвенно всех аспектов любого прикладного или теоретического знания.

Отличительными особенностями её являются:

использование особой знаковой системы (цифры, буквы разных алфавитов, языковые правила и т.д.),

логическая строгость (понятия, определения, суждения, правила вывода задаются в явном и точном виде),

последовательность (не поймёшь пункт 3, если не понял пункты 1 и 2),

высокая плотность информации на единицу текста (часто смысла в тексте гораздо больше, чем в текстах иного содержания).

Легко показать, что любой интеллектуально развитый человек регулярно использует те же мыслительные конструкции, что и математика. Когда мы говорим давайте рассмотрим десять каких-либо операций (алгоритм) вроде кулинарного рецепта или простейшей программы или рассмотрим какой-либо частный случай явления, определим его свойства, отношения с другими явлениями, изучим структуру — мы прибегаем к универсальным способам мышления, которые характерны для любого знания и в том числе математического.

Эта статья никогда бы не появилась на свет, если бы учебная литература была бы настолько совершенна, что могла бы легко объяснить, что такое интеграл. Перечитав десятки книг и статей я с уверенностью могу сказать, что ни одна из них не объясняет все нюансы этого вопроса так и таким образом, чтобы среднему, неискушённому человеку было всё абсолютно ясно.

Многие источники не удовлетворительны по следующим причинам:

Говорят о какой-то площади под кривой при том, что читатель ни сном, ни духом не задумывался о площади, тем более под кривой и какой-то связи этой площади с универсальной идеей суммирования переменных величин

Без интуитивного подведения читателя через сложение и умножение чисел, основательного разъяснения связи …. сразу бросаются к определению интеграла через предел римановской суммы

Забывают рассказать об историческом процессе развития математики (зачем ввели интеграл, какие открытия этому предшествовали, что подвело к этому, как считали интегральные суммы до этого, как Ньютон и Лейбниц считали интегралы и т.д.)

Не считают нужным или не хотят привести пару тройку простых примеров интегрирования из прикладных наук

Сыпят доказательствами утверждений, которые новичку покажутся неуместными или второстепенными

Забывают напомнить выводы, обозначения и утверждения, использованные или доказанные ранее

Пропускают те или иные алгебраические преобразования, которые «очевидны» автору, но могут запутать новичка

Автору надоело чувствовать неясность и он решил взять дело в свои руки — расписать все аспекты так, чтобы было всё предельно ясно и понятно.

1. Предпосылки возникновения интегрирования

Интеграл и интегрирование являются неотъемлемыми и последовательными элементами исследования величин и функций. Интегрирование теснейшим образом связано с важнейшими способами анализа и исследования числовых функций — средними, предельными, бесконечно малыми, бесконечно большими величинами, пределами, дифференциалами, производными и т.д. А потому, без осознания и исследования этих понятий невозможно и формирование понятия интеграла.

Исторически и логически они развивались и развиваются слитно и нераздельно.

Как известно осознание самостоятельной значимости и полноценное развитие математики начались в Древней Греции. Постепенное накопление прикладных знаний о различного рода вычислительных, логических и геометрических задачах неизбежно привело к формированию теоретических начал и абстрактных представлений о существе многих математических идей.

Корпус прикладных и теоретических знаний накапливался и формировался шаг за шагом за счёт осмысления логического устройства мышления, применения арифметических операций, составления и решения алгебраических уравнений, построения и изучения свойств плоских и объёмных геометрических фигур.

2. Геометрический и аналитико-алгебраический смысл интегрирования

Согласно дошедшим до нас источникам, именно отыскание квадратуры является первой формой постановки задачи интегрирования. Задача явно сформулирована и решена в трудах Евдокса Книдского (сформулировал метод исчерпывания, позднее развитый в XVI веке в метод неделимых), Евклида и Архимеда. Древнегреческих математиков интересовали задачи отыскания площади круга, поверхности сферы, сегмента параболы, а также объёма шара, цилиндра, пирамиды, конуса, тетраэдра и ряда других геометрических фигур.

Под проведением квадратуры понималось построение с помощью циркуля и линейки квадрата, равновеликого заданной фигуре (то есть имеющего такую же площадь) или прямое вычисление соответствующей площади. Вероятно связи геометрии и анализа если и обнаруживались, то интуитивно и неявно. Во всяком случае координатный метод и понятия дифференциального исчисления точно не были известны, хотя и почти что точно были так или иначе интуитивно восприняты и неявно затронуты.

Что касается второго типа задач. Интегралы часто описываются как площадь под кривой. Это описание сбивает с толку. Точно также, как если сказать, что умножение — это нахождение площади прямоугольника. Именно понимание сущности умножения применительно к различного рода частным случаям позволяет понять аналитико-алгебраическую суть интегрирования.

Понимание и использование простейших случаев умножения, к примеру, умножения натуральных чисел, было известно с древнейших времён.

Однако, за всеми частными случаями умножения находится определённая общность. Вот как можно описать умножение чисел из различных числовых множеств:

В случае с натуральными числами. К примеру, умножим число 3 на число 4, то есть 3 × 4. Умножение — это повторяющееся сложение, то есть произведение чисел получим сложив число три четыре раза или наоборот сложив число четыре три раза [3].

В случае с вещественными числами.

Возьмём одно рациональное число — дробь, а другое целое. К примеру, умножим 3,5 на 2, то есть — 3,5 × 2. Умножение — это повторяющееся сложение, произведение получим сложив число три целых и пять десятых два раза. Также, получить произведение можно путём сложения произведений вначале целой части числа 3,5 то есть 3 на 2, а затем дробной то есть 0,5 на 2. Для целой части — сложим число три два раза, а для дробной части — возьмём единицу разделим на десять, затем возьмём пять частей от деления то есть пять десятых и сложим два раза.

Возьмём два рациональных числа — две дроби и получим произведение. К примеру, умножим 3,5 на 2,1 то есть — 3,5 × 2,1, произведение получим сложив произведение 3,5 на 2 и 3,5 на 0,1 [4]. Словесно это будет выглядеть следующим образом, для первого произведения — сложим число три целых пять десятых два раза, для второго — разделим число три целых пять десятых на десять частей и возьмём одну часть то есть одну десятую.

В случае с комплексными числами (3 × 3i), умножение выступает вращением и масштабированием.

Мы ходим вокруг да около «применения» одного числа к другому, и действия, которые мы применяем (повторное суммирование, масштабирование, зеркальное отображение или вращение), могут быть разными. Интегрирование — это всего лишь еще один шаг в этом направлении.

Когда мы умножаем числа мы повторяем сложение, где в каждом слагаемом знаем какие находятся операнды, а именно — повторяющиеся числа.

К примеру, если мы хотим вычислить пройденный путь телом, движущимся с одинаковой скоростью в каждый момент времени, то мы просто перемножим скорость на время (значение функции скорости одинаково, а геометрически грубо говоря одинаково во всем прямоугольнике).

Но изменяющаяся скорость требует совмещения скорости и времени по частям (момент за моментом, секунда за секундой). В каждый момент скорость может быть разной.

Вот как это выглядит в большой перспективе:

Обычное умножение (прямоугольник): берем расстояние, на которое мы продвинулись за секунду, предполагая, что эта величина была постоянной во все последующие секунды движения, и «масштабируем ее».

Интегрирование (по частям): рассматриваем время как ряд мгновений, в каждое из которых скорость разная. Суммируем расстояния, пройденные в каждое из мгновений (секунд, миллисекунд и т. д.).

То есть, интегральную сумму (значение интеграла, определённый интеграл) можно определить, как максимально точную сумму значений искомой переменной величины

при её изменении в промежутке от до где а .

Точность достигается в пределе, то есть при всё большем уменьшении размера промежутков между значениями или, что тоже самое, при всё большом увеличении числа отрезков (числа — обозначающего индекс-номер последнего отрезка)

Несомненно греческих и более поздних мыслителей интересовали задачи на отыскание суммарного значения переменных величин. Вероятно их устраивало простое суммирование значений переменной величины, приближённые вычисления. Если мы возьмём приращение переменной равное единице, то интеграл приближённо будет равен сумме значений функции в рассматриваемом промежутке.

В дальнейшем, начиная с XVI века (работы Галилея, Кеплера, Кавальери и других о методе неделимых) понимание интегрирования постепенно совершенствовалось и развивалось пока не достигло формализации у Бернхарда Римана в середине XIX века и дальнейшего обобщения.

3. Интуитивные способы отыскания значения интеграла

Умножить совокупное приращение переменной на значение функции и получить площадь прямоугольника, который добавит значительный излишек, либо срежет значительную часть в зависимости от того какое значение функции мы выберем. Вручную мы можем подобрать такое значение функции, что при умножении её на приращение переменной мы получим довольно точное значение площади (определённого интеграла в промежутке). Для этого нам потребуется провести линию так, чтобы площадь излишка примерно равнялась срезанной площади. Однако, это не даст нам универсального метода отыскания значения искомой величины.

2. Сложить произведения приращения переменной на значение функции в соответствующих точках, получив тем самым сумму площадей прямоугольников, внешне напоминающих лестницу (ступеньки). В самом простом случае приращение равно единице. На этом методе и основано формальное определение определённого интеграла, данное Б. Риманом. О нём мы поговорим ниже.

3. Воспользоваться иными так называемыми численными способами отыскания значения интегральной суммы (интеграла).

4. Отыскание значения интеграла через отыскание первообразной

Однако есть более изящный и универсальный способ вычисления интегральной суммы, который был открыт Исааком Ньютоном и Готфридом Лейбницом. Этот способ устанавливает фундаментальную связь дифференцирования (производной) и интегрирования (первообразной).

Чтобы рассмотреть суть открытия, необходимо последовательно прийти к ряду идей и рассуждений.

Пусть имеется некоторая функция от числовой переменной — Обозначим её [5].

Следует отметить несколько обстоятельств относительно рассматриваемой функции:

Функция является числовой, то есть область определения и область значений являются числовыми — принимают числовые значения (более точно — вещественные значения).

Функция непрерывна и принимает значения в каждой точке с соответствующим значением переменной (к примеру, в точкесуществует значение функции , а в точке значение

Функция может иметь любое выражение. Мы можем иметь набор значений функции в соответствующих точках в виде таблицы (функция задана таблично). Или функция может быть явно задана в виде аналитического выражения (к примеру, в случае с функцией от одной вещественной переменной — , и т.д.).

Функция может описывать зависимость величины любой природы — физической, биологической, экономической и т.д.

Для наглядности изобразим график рассматриваемой функции в виде произвольной кривой.

Пусть мы хотим отыскать всю или часть совокупного значения (аналитико-алгебраический смысл интегрирования) или площадь под кривой (геометрический смысл). Выберем промежуток между двумя точками и и продолжим наши рассуждения.

Искомое значение представляет собой функцию и очевидно, что оно будет зависеть от размера промежутка и того значения изначальной функции, которое она принимает в каждой точке этого промежутка. Также, очевидно, что промежуток значений переменной для изначальной функции и функции площади будет одинаковым [6].

Сказанное выше легко показать и увидеть на графике.

Заметим, что значения функции площади не равны значению изначальной функции при том же значении переменной [7]. Значения площади постоянно возрастает слева-направо, то есть при каждом шаге приращения промежутка суммирования (интегрирования).

Пусть теперь исследуемая функция является функцией скорости движения материальной точки (тела) по некоторой траектории. Тогда, очевидно, по определению производной, что скорость в конкретный момент времени — это первая производная пути (координаты) по времени

Если скорость это производная пути и мы знаем аналитическое выражение её выражающее, то мы можем найти выражение для самого пути то есть для самой функции. Мы можем это сделать через операцию, обратную нахождению производной то есть через отыскание первообразной. Это справедливо, поскольку производная и соответствующее ей семейство первообразных единственны.

Данный вывод можно обобщить на все интегрируемые функции.

Далее, легко понять из простых арифметических и геометрических соображений, что значение интегральной суммы (площади) будет равно разности значений полученной функции (первообразной), взятых в соответствующих точках [8].

То есть если требуется найти интегральную сумму в промежутке от до , где первое и второе — некоторые произвольные значения переменной, то необходимо вычислить разность

Указанная сумма и есть определённый интеграл, который записывается, как

[2]. Имеется ввиду сумма значений переменной, которая является элементом интегрирования, интегрируемой величиной.

[3]. Не имеет значения каким образом будем вычислять произведение, так как от перестановки множителей произведение не меняется, то есть данная операция обладает свойством коммутативности.

[4]. 3,5 · 2 + 3,5 · 0,1 = 3,5 (2 + 0,1) = 3,5 · 2,1.

[5]. Вместоможет быть любое обозначение, к примеру, — это не имеет значения. Буквавсего лишь обозначает имя для функции, а скобки отделяют имя от сущностей — обычно числовых переменных над которыми совершаются те или иные операции, дающие в результате значение функции.

[6]. Переменная-аргумент — одна и таже, то есть иными словами значения переменной-аргумента в точках для и одно и тоже. Далее, мы покажем, что производная , то есть можно записать или .