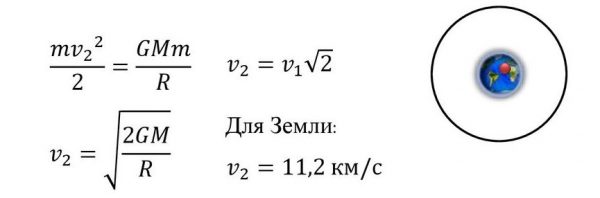для чего нужны космические скорости
Космические скорости
Любой предмет, будучи подброшенным вверх, рано или поздно оказывается на земной поверхности, будь то камень, лист бумаги или простое перышко. В то же время, спутник, запущенный в космос полвека назад, космическая станция или Луна продолжают вращаться по своим орбитам, словно на них вовсе не действует сила притяжения нашей планеты. Почему так происходит?
На нашей Земле всемирное тяготение воздействует на любое материальное тело. Тогда логично будет предположить, что есть некая сила, нейтрализующая действие гравитации. Эту силу принято называть центробежной.
Центробежную силу легко ощутить привязав на один конец нитки небольшой груз и раскрутив его по окружности. При этом чем больше скорость вращения тем сильнее натяжение нити, а чем медленнее вращаем мы груз тем больше вероятность, что он упадет вниз.
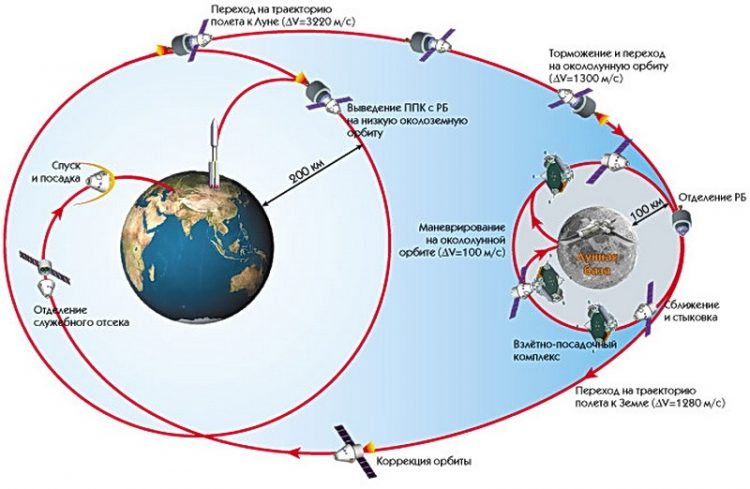
Траектория полета космических кораблей
Таким образом мы вплотную приблизились к понятию «космическая скорость». Простыми словами — это скорость, позволяющая любому объекту преодолеть тяготение небесного тела и их системы. Космические скорости используются для характеристики типа движения космического аппарата в сфере действия небесных тел: Солнца, Земли и Луны, других планет и их естественных спутников, а также астероидов и комет.
Это также значит, что космическая скорость есть у каждого объекта, который движется по орбите. Размер и форма орбиты космического объекта зависят от величины и направления скорости, которую данный объект получил на момент выключения двигателей, и высоты, на которой произошло данное событие.
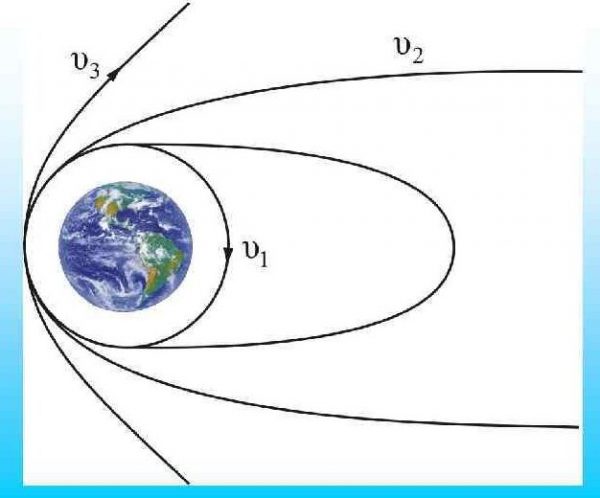
Космическая скорость (первая v1, вторая v2, третья v3 и четвёртая v4) — это минимальная скорость, при которой какое-либо тело в свободном движении сможет:
Космические скорости могут быть рассчитаны для любого удаления от центра Земли. Однако в космонавтике часто используются величины, рассчитанные конкретно для поверхности шаровой однородной модели Земли радиусом 6371 км.
Первая космическая скорость
Первая космическая скорость или Круговая скорость V1 — скорость, которую необходимо придать объекту без двигателя, пренебрегая сопротивлением атмосферы и вращением планеты, чтобы вывести его на круговую орбиту с радиусом, равным радиусу планеты.
Иными словами, первая космическая скорость — это минимальная скорость, при которой тело, движущееся горизонтально над поверхностью планеты, не упадёт на неё, а будет двигаться по круговой орбите.
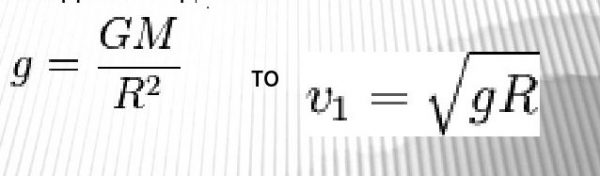
Формула
где G — гравитационная постоянная (6,67259·10−11 м³·кг−1·с−2), — первая космическая скорость. Подставляя численные значения (для Земли M = 5,97·1024 кг, R = 6 378 км), найдем
7,9 км/с
Первую космическую скорость можно определить через ускорение свободного падения —
Вторая космическая скорость
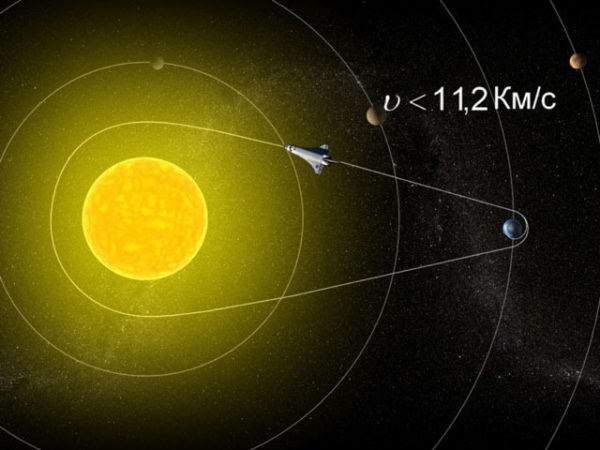
Вторая космическая скорость (параболическая скорость, скорость убегания) — наименьшая скорость, которую необходимо придать объекту (например, космическому аппарату), масса которого пренебрежимо мала относительно массы небесного тела (например, планеты), для преодоления гравитационного притяжения этого небесного тела.
Предполагается, что после приобретения телом этой скорости оно не получает негравитационного ускорения (двигатель выключен, атмосфера отсутствует).
Вторая космическая скорость определяется радиусом и массой небесного тела, поэтому она своя для каждого небесного тела (для каждой планеты) и является его характеристикой:
Параболической вторая космическая скорость называется потому, что тела, имеющие вторую космическую скорость, движутся по параболе.
Формула
Третья космическая скорость
Третья космическая скорость — минимально необходимая скорость тела без двигателя, позволяющая преодолеть притяжение Солнца и в результате уйти за пределы Солнечной системы.
Только на космических кораблях, которым доступны такие скорости, принципиально могут быть осуществлены пилотируемые межзвёздные перелёты к планетным системам других звёзд.
Взлетая с поверхности Земли и наилучшим образом используя орбитальное движение планеты космический аппарат может достичь третей космической скорости уже при 16,6 км/с относительно Земли, а при старте с Земли в самом неблагоприятном направлении его необходимо разогнать до 72,8 км/с.
Здесь для расчёта предполагается, что космический аппарат приобретает эту скорость сразу на поверхности Земли и после этого не получает негравитационного ускорения (двигатели выключены и сопротивление атмосферы отсутствует). Если к тому же учесть притяжение других планет, которое может как ускорить, так и притормозить аппарат, то диапазон возможных значений 3-й космической скорости станет еще больше.
При наиболее энергетически выгодном старте скорость объекта должна быть сонаправлена скорости орбитального движения Земли вокруг Солнца. Орбита такого аппарата в Солнечной системе представляет собой параболу.
Четвёртая и пятая космическая скорости
Четвёртая космическая скорость — минимально необходимая скорость тела без двигателя, позволяющая преодолеть притяжение галактики Млечный Путь. Она используется довольно редко.
Четвёртая космическая скорость не постоянна для всех точек Галактики, а зависит от расстояния до центральной массы.
Для нашей галактики таковой является объект Стрелец A*, сверхмассивная чёрная дыра.
По грубым предварительным расчётам в районе нашего Солнца четвёртая космическая скорость составляет около 550 км/с. Значение сильно зависит не только (и не столько) от расстояния до центра галактики, а от распределения масс вещества по Галактике, о которых пока нет точных данных, ввиду того что видимая материя составляет лишь малую часть общей гравитирующей массы, а все остальное — скрытая масса.
Ещё реже в некоторых источниках встречается понятие «пятая космическая скорость». Это скорость, позволяющая добраться до иной планеты звездной системы вне зависимости от разности плоскостей эклиптики планет. Например, для Солнечной системы и, конкретно, для Земли, чтобы орбита межпланетного перелета была перпендикулярной к земной орбите, нужна скорость запуска 43,6 километра в секунду.
Видео
Космические скорости
«Поехали!»
В 1957 году работа советских учёных, конструкторов, инженеров, рабочих, во главе с Сергеем Павловичем Королёвым, увенчалась блестящей победой: 4 октября они вывели на орбиту первый в истории искусственный спутник Земли. А 12 апреля 1961 года отправили в первый космический полёт человека — Юрия Алексеевича Гагарина. На весь мир прозвучало знаменитое гагаринское «Поехали!», и человечество вступило в космическую эру.
Космическая тематика стремительно вошла в моду. Естественно, появились новые темы и понятия — ракеты, скафандры, невесомость, первая космическая скорость, вторая космическая скорость. Все мальчишки нашего поколения в мечтах примеряли скафандр космонавта. О невесомости мы поговорим в другой раз, а пока рассмотрим космические скорости.
Что известно о космических скоростях простым людям
На телевидении есть передача, в которой весёлый молодой человек бегает по улицам и задаёт прохожим разные вопросы. За правильный ответ он вручает 1000 рублей. Однажды он задал такой вопрос: «Какую скорость надо развить, чтобы оторваться от Земли?» Первый встречный ответить не смог, и ведущий буквально клещами вытащил из второго ответ, который был признан правильным: «Вторую космическую».
Увы, молодой человек ошибся. Вернее, ошибся не он, а редакторы, придумывающие вопросы и ответы к ним. Точно так, как и редакторы, считают почти все, кто хоть отдалённо слышал про существование первой и второй космических скоростей.
На самом деле, чтобы оторваться от Земли, подходит любая скорость. Уже когда ребёнок подпрыгивает, он отрывается от Земли. Пусть ненадолго, но отрывается. И вообще, до Луны или до другого космического объекта можно добраться с любой скоростью. Для этого надо немного разогнаться, а потом поддерживать силу тяги двигателя, равную силе земного притяжения, и вы будете «бороздить просторы Вселенной» с постоянной скоростью. Более того, если представить, что какой-то чудак сумел построить лестницу до Луны, то вы сможете подняться туда просто пешком. Примерно так, как вы поднимаетесь к себе домой на третий этаж, только гораздо дольше.
А как же космические скорости? Космические скорости подразумевают, что ракета, достигнув их, дальше летит к намеченной цели по инерции, с неработающим двигателем. Это только в мультфильмах про космические путешествия показывают летящие ракеты с работающим двигателем. Но это исключительно для создания иллюзии движения.
Если же в реальных условиях двигатель у ракеты будет работать постоянно, то даже для полёта на Луну потребуется такое количество топлива, что его ни одна ракета не осилит.
Постреляем
Первая космическая скорость
Первая космическая скорость — это скорость, с которой надо горизонтально запустить объект, чтобы он стал вращаться вокруг Земли по круговой орбите.
Чем больше высота, с которой мы запускаем объект, тем меньше эта скорость. Например, Международная космическая станция летает на высоте 400 км со скоростью 7,6 км/с, а Луна — на расстоянии 384 500 км от Земли со скоростью 1 км/с. «Нулевой» высоте соответствует скорость 7,9 км/с, что обычно и называют первой космической скоростью.
Точно так же Земля вращается вокруг Солнца почти по круговой орбите со скоростью ≈ 30 км/с. Это и есть первая космическая скорость относительно Солнца на таком расстоянии от него.
Если скорость спутника чуть больше первой космической для его высоты, его орбита будет эллипсом. Все спутники вокруг Земли и планеты вокруг Солнца движутся именно по эллипсам. И орбиты комет — тоже эллипсы, только очень вытянутые, так что кометы улетают по ним «в даль тёмную», лишь изредка возвращаясь к Солнцу «погреть бока».
Иными словами, первая космическая скорость — это минимальная скорость, при которой тело, движущееся горизонтально над поверхностью планеты, не упадёт на неё, а будет двигаться по круговой орбите.
Вторая космическая скорость
Вторая космическая скорость — наименьшая скорость, которую необходимо придать космическому аппарату для преодоления притяжения планеты и покидания замкнутой орбиты вокруг неё.
Предполагается, что аппарат не вернётся на планету, улетит в бесконечность. На самом деле тело, имеющее около Земли такую скорость, покинет её окрестности и станет спутником Солнца. Вторая космическая скорость в \(\sqrt <2>≈ 1<,>4\) раза больше первой космической.
Третья космическая скорость
Третья космическая скорость — минимальная скорость, которую необходимо придать находящемуся вблизи поверхности Земли телу, чтобы оно могло преодолеть притяжение не только Земли, но и Солнца, и покинуть пределы Солнечной системы.
Космические достижения
Первый искусственный спутник Земли был шариком диаметром 58 см и передавал только звуковой сигнал «бип-бип-бип». Но первая космическая скорость была достигнута! А всего через год, 2 января 1959 года, космический аппарат «Луна-1» полетел, естественно к Луне, со второй космической скоростью.
Пока с наибольшей скоростью 16,26 км/с покидала Землю автоматическая межпланетная станция «Новые горизонты», запущенная в США 19 января 2006 года. Относительно Солнца её скорость составляла 45 км/с — благодаря тому, что запускалась она в сторону движения Земли по орбите.
Конические сечения
Вернёмся к движению тела вокруг одного источника притяжения, например Солнца. Если тело запустить с первой космической перпендикулярно направлению на Солнце, оно полетит по окружности. Если запустить его в любом направлении, только не на само Солнце, со скоростью меньше второй космической, орбита будет эллипсом. При запуске со второй космической получится парабола. Если запустить с ещё большей скоростью, получится гипербола.
Эти кривые можно увидеть, пересекая конус плоскостью. Если ось конуса перпендикулярна плоскости, в пересечении получится окружность. Будем постепенно менять угол наклона плоскости к оси конуса. Линия пересечения превращается в эллипс, причём чем больше угол наклона, тем более вытянутым получается этот эллипс. Продолжим наклонять секущую плоскость до тех пор, пока она не станет параллельной одной из касательных плоскостей конуса. В этот момент линия пересечения — парабола. Наклоним ещё — получится гипербола.
Художник Мария Усеинова
1 Подробнее об этом читайте в «Квантике» №11 за 2016 год, с. 2–5.
Космические скорости
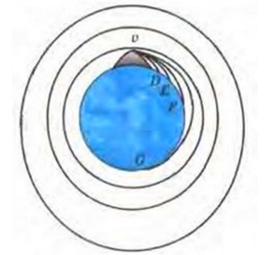
Если прилагать больше сил при бросании, то он упадет дальше. Отсюда следует, что при отсутствии сопротивления воздуха и при наличии большой скорости тело может даже не приземляться на поверхность. Это говорит о его дальнейшем описывании круговых траекторий, не изменяя высоты относительно земной поверхности.
Первая космическая скорость
Вторая космическая скорость
Для ее нахождения следует произвести вычисление работы, потраченную против сил земного притяжения для соударения с поверхности Земли на бесконечность. При удалении такого тела получаем:
Существует связь между первой и второй скоростями
Квадрат скорости убегания равняется ньютоновскому потенциалу в заданной точке, то есть:
Нужная величина скорости не зависит от направления движения тела. На это влияет вид траектории, по которой происходит удаление от земной поверхности.
Чтобы тело смогло стартовать с поверхности планеты, оно должно обладать второй космической скоростью при малом значении h и большом значении гравитационной силы. Как только ракета начнет удаляться от Земли, гравитационная постоянная будет уменьшаться вместе со значением, необходимым для убегания кинетической энергии.
Третья космическая скорость
Еще в СССР были достигнуты космические скорости.
Дано:
Решение
Значение g принимает ускорение свободного падения на Юпитере.
Значение m определено как масса спутника, а М – масса самой планеты.
Получаем, что из уравнения ( 2 ) найдем ускорение свободного падения для планеты из
Космические скорости или как свалить с этой планеты
Вот подходит к концу 2020 год и становится всё очевидней, что с этой планетой что то пошло не так. И всё больше и больше людей задумываются о переезде на другую планету. В этой статье я и расскажу вам о Первой и Второй космической скорости.
Многие скажут:- Ракеты всё равно стоят миллиарды долларов, которых у меня нет. Зачем мне всё это?
Вы не учитываете инопланетян которые регулярно спасают людей от этой планеты (Малдер врать не будет). И не факт, что они спасают людей с красивыми глазками. Если сравнивать например с кошками, то не всё люди заводят себе красивых кошек — многие предпочитают умных. К тому же умных кошек обычно заводят умные хозяева, а следовательно — умных кошек мучают реже, чем красивых.
Поэтому вряд ли высокоразвитая цивилизация, заберет человека — не знающего про Космические скорости. Да, это лишь небольшая вероятность, но те кто не знают про космические скорости — гарантированно останутся в этом обезьяннике. В этой статье вы узнаете о космических скоростях, как они складываются (если прыгнуть вверх с начальной скоростью 15 км/с — с какой скоростью вы вылетите?) и вообще о том как работает гравитация (по ламповой Ньютоновской физике) на максимально простых примерах.
Что такое энергия?
И этот совет реально изменил мою жизнь, на следующий день из меня вышла черепаха, я начал нормально спать, у меня прошла тахикардия и я сказочно разбогател, но главное не деньги — самое главное что у меня наступила душевная гармония. И это реально работает. Поэтому давайте просто сравним и посчитаем 2 энергии на простых примерах.
Хороший и полезный пример, это 2 одинаковых автомобиля тормозящие перед препятствием.
2 автомобиля едут с разной скоростью рядом друг с другом (слева/справа).
Первый 70 км/ч
Второй 100 км/ч
Перед ними внезапно появляется препятствие и они начинают одновременно тормозить. Первый полностью успевает затормозить с 70 до 0 в миллиметре от препятствия. С какой скоростью в стену влетит второй, ехавший 100 км/ч?
Британские учёные считали в милях, но — что в километрах в час, что в метрах в секунду результат получится одинаковый (соотношение сохранится). Итак, по условию задачи — автомобили одинаковые, тормозной путь одинаковый и производительность тормозов тоже одинаковая.
Давайте посчитаем энергию (масса*скорость в квадрате/2). Для удобства, возьмем массу автомобилей 2 кг. тогда энергия будет равна просто скорость в квадрате.
Итого начальная энергия первого была 70*70=4900. Он полностью остановился, следовательно он потерял 4900 энергии.
Тормоза у второго были точно такие же и следовательно он так же потерял 4900, но его изначальная энергия была 100*100=10 000, вычитаем 4900, и остается 5100. Т.е. у него осталось больше энергии, чем у первого было изначально = он влетит в стену со скоростью больше 70 км/ч. Чтобы получить скорость из энергии, нужно извлечь из неё квадратный корень 5100=71,41 км/ч.
Из всего этого нам нужно понять квадратичную связь между скоростью и энергией, скорость в 2 раза больше = тормозной путь в 4 раза длиннее. Похожую картину можно наблюдать и в мощностях двигателей.
Например какой-нибудь фольксваген с 400 лошадиными силами легко разгоняется до 200 км/ч, а у бугатти вейрон 1600 л.с и она кое-как разгоняется до 400 км/ч.
Хотя пример с двигателями не совсем отражает суть кинетической энергии (энергии текущей скорости), потому что двигатель автомобиля тратит энергию не только на ускорение, а еще и на трение и «толкание» атмосферы. В чистом вакууме и без гравитации — разогнавшись до 100 км/ч — вы никогда не остановитесь.
В космическом пространстве трения нет, но гравитация есть везде. Теперь давайте разберемся с тем, что же такое гравитация и как она работает, а для удобства мы будем рассматривать ровно вертикальный старт.
О потенции и её энергии
Возьмем 2 выстрела с начальной скоростью 100 и 200 м/с и ускорение свободного падения 10 м/с (за секунду).
Первое ядро при начальной скорости 100 м/с поднялось на высоту 500 метров.
Второе ядро при начальной скорости 200 м/с поднялось на высоту 2000 метров.
И тут мы видим ту же самую квадратичную зависимость, при скорости в 2 раза больше высота увеличивается в 4 раза. Пороха второму ядру естественно понадобится в 4 раза больше (иначе, мы бы смогли построить вечный двигатель).
Теперь давайте посчитаем начальную энергию, для удобства давайте возьмем массу ядер 2 кг., тогда энергия будет равна просто скорость в квадрате.
Энергия первого ядра была 100*100=10 000 Джоулей (высота 500 метров)
Энергия второго ядра была 200*200=40 000 Джоулей (высота 2 000 метров)
Итого — чтобы подняться на высоту 500 метров нужно 10 000 Джоулей энергии.
Часто возникает вопрос, можно ли подняться дешевле? Второе ядро прошло 500 метров меньше чем за 3 секунды, и оно потеряло в скорости всего
30 м/с, зависит ли потерянная энергия от текущей скорости?
Для удобства, я подобрал 2 начальных скорости, при которых ядро пройдет 500 метров ровно за 1 секунду, и за 2 секунды.
При начальной скорости 260 м/с, ядро пролетит 500 метров ровно за 2 секунды и потеряет 20 м/с скорости, но в этих 20 м/с будет ровно 10 000 Дж энергии (или можно сказать по другому — чтобы разогнаться с 240 м/с до 260 м/с нужно 10 000 Дж. Энергии).
Тоже самое будет и при скорости 505 м/с, потерянная энергия составит те же 10 000 Дж, за 500 метров.
На самом деле формула энергии и была определена с помощью гравитации. Теперь давайте возьмем ускорение свободного падения 1 м/c (секунда в квадрате означает ускорение каждую секунду на 1 метр в секунду) и опять посмотрим на высоту (начальную скорость тоже уменьшим, до 10 м/с).
При ускорении свободного падения 1 м/с и начальной скорости 10 м/с = мы поднимемся на 50 метров, а 50 это у нас что? Это 10 в квадрате (10*10=100) делить на 2. Вот мы и получили формулу энергии.
Ускорение называют Ньютонами (1 м/с=1 Н).
А результат (работу) называют Джоулями, чтобы поднять 1 кг. на 1 метр нужна энергия 1 дж. (при ускорении свободного падения 1 м/с).
Из всего этого Ньютон и построил свою механику.
И благодаря ей, люди научились мериться не только своими сантиметрами, но и целыми конскими метрами. Люди начали массово проверять, чей конь поднимет массу на большую высоту, у того и больше метров. Естественно конские метры были не у всех, и лошади начали активно продвигать идею, что метры не важны — главное Сила (ускорение), а еще время тоже очень важно. И силу нужно еще умножать на время.
Но кони лишь ржали. И говорили:- если лошадиные силы так важны, то почему беременная лошадь бежит медленнее, чем не беременная? — Время ни на что не влияет. Главное результат.
Ну и в конечном итоге, как это часто бывает у лошадей, они внезапно заявили — что 1 лошадиная сила равна 735,5 конских метров. Почти километр. Просто вынь да положь. Лошади всегда были такими, и как всем известно, если лошадь что то придумала, то переубедить её невозможно, и за 400 лет ни одну лошадь переубедить так никому и не удалось. 1 лошадиная сила так и осталась равна 735,5 конским метрам.
Итак, плата за высоту зависит только от расстояния, а не от времени или скорости. И чтобы подняться на определенную высоту, мы потеряем определенную энергию.
Есть ли максимальная высота? И да и нет, хотя дальность действия гравитации бесконечна, и вы можете улететь хоть в другую галактику, и каждая Русская Березка будет тянуть вас обратно, но суммарная энергия гравитации не бесконечна — Потому что гравитация уменьшается с расстоянием. Если сильно упростить формулы:
Представьте что у вас есть например 10 Дж. энергии →вы отдалились от притягивающего тела в 2 раза и потеряли 5 Дж., теперь у вас в 2 раза меньше энергии, но и гравитация стала слабее в 2 раза, и на следующем шаге вы потеряете уже 2,5 Дж. и так до бесконечности — у вас становится меньше энергии, но и гравитация становится слабее — вы будете бесконечно замедляться, но никогда не остановитесь. Если формулы не упрощать, то будет опять та же квадратичная зависимость (только обратная) — отдалившись от центра в 2 раза — гравитация станет слабее в 4 раза (2*2), отдалившись в 10 раз дальше, гравитация станет в 100 раз слабее (10*10).
Эту максимальную энергию высоты и называют Второй космической скоростью (скорость убегания или параболическая траектория) для Земли это 125 440 000 Дж (за каждые 2 кг) или 11 200 м/с. (квадратный корень из 125 440 000). При такой энергии вы будете бесконечно замедляться, но никогда не остановитесь. Если у вас изначально будет хотя бы на 100 Дж. больше, то ваша энергия никогда не станет меньше 100 Дж., а ваша скорость отдаления от Земли никогда не станет меньше 10 м/с (корень из 100). Если у вас изначально будет меньше энергии — то гравитация вас развернет и вернет вам все ваши Джоули. Суммарна плата за выход всегда одинаковая.
Так же существует Первая космическая скорость (Движение по идеальному кругу), которая ровно в 2 раза меньше по энергии или в
1,41 раз по скорости (корень из 2). Для Земли это 62 720 000 Дж. (за 2 кг.) или 7 920 м/с. Двигаясь с такой скоростью вокруг земли, вы никогда не коснетесь её поверхности. Грубо говоря, за каждую секунду вы будете падать на 10 м вниз, но ещё за эту же секунду вы будете перемещаться на 7,92 км вперед и из-того что земля круглая, поверхность тоже будет уходить вниз (упрощенно на 10 м за секунду). Таким образом, вы будете всегда находится на одной и той же высоте от поверхности и двигаться с одной и той же скоростью.
При скорости выше первой, но меньше второй — орбита будет эллиптической, здесь мы её рассматривать не будем, но если в 2-х словах, то у вас всегда будет меняться и скорость, и высота, но сумма их энергий будет всегда одинаковая.
Это условно 2 максимальные космические скорости, при старте с поверхности (с нулевой высоты). Так же можно выделить локальные космические скорости, для каждой высоты они будут свои. Формулы я расписывать не буду (их очень легко найти в той же Википедии), я лишь объясню их в общих чертах. Чем выше вы находитесь, тем больше энергии вы уже «заплатили за высоту» и тем меньше вам еще осталось. К примеру на высоте 35 786 км. (Геостационарная орбита), Вторая космическая скорость будет равна 4,35 км/с, Первая космическая скорость для этой высоты (идеально круглая орбита) — будет так же ровно в 2 раза меньше по энергии или в
1,41 раз меньше по скорости. 4,35/1,41 = 3,08 км/с.
Физический смысл имеют только первые 2 космические скорости, но литературно выделяют еще несколько.
3-я космическая. — скорость убегания из Солнечной системы
42 км/с — это при старте с орбиты Земли, (посчитаем её чуть дальше)
4-ая космическая — скорость убегания из нашей галактики
550 км/с, но это не точно, потому что нам надо знать распределение массы по галактике.
Ну и конечно 5-ая космическая скорость — это скорость убегания из нашей вселенной, нужно просто двигаться быстрее света. Но она еще не изучена учеными, потому что я только что её придумал.
Скорости выше 2-ой имеют только литературный смысл, работают они точно так же как и первые 2.
Как складываются космические скорости?
Давайте посчитаем 3-ю космическую — как убежать от Солнца.
Начнем с примера в вакууме без Солнца.
Прыгаем вверх с Земли со скоростью 15 км/с, с какой скоростью мы вылетим с Земли?
Дальность гравитации бесконечна, но на высоте 1 000 000 км. (в 3 раза дальше луны) мы «заплатим» уже
99,37% от необходимой энергии (остальные 0,63% энергии мы «заплатим» за бесконечное расстояние), поэтому если мы ограничим гравитацию таким расстоянием, то не сильно ошибемся. (миллион километров — это не так много, от Земли до Солнца
150 миллионов, а до Нептуна
4,3 миллиарда км.). Вернее мы вообще не ошибемся, мы ограничим дальность несколькими км., но сумму энергии возьмем все 100%.
Итак вторая космическая для Земли 11,2 км/с, мы прыгаем 15 км/с.
Чтобы узнать скорость вылета, нужно вычитать энергию Второй космической скорости из энергии старта. Прыгать кстати можно в любую сторону под любым углом, от этого поменяется только угол вылета, сама скорость убегания всегда будет 10 км/с относительно Земли.
Теперь давайте посчитаем 3-ю космическую, как нам убежать не только от Земли, но еще и от Солнца.
Земля двигается вокруг Солнца со скоростью
29,783 км/с, при этом орбита немного вытянута. Но давайте округлим орбитальную скорость до 30 км/с, и еще округлим орбиту до идеального круга. Тогда получится что 30 км/с — это Первая космическая скорость на высоте
150 млн. км., а это значит, что Вторая космическая для этой высоты в 2 раза больше по энергии или в 1,41 раз больше по скорости (корень из 2-х).
42,3 км/с = чтобы убежать от Солнца нам нужно двигаться 42,3 км/с.
30 км/с у нас есть (мы двигаемся вместе с Землёй с этой скоростью), нам нужно 42,3 км/с, т. е. Нам нужно вылететь со скоростью 12,3 км/с относительно Земли (42,3-30=12,3).
Дальше считаем как в прошлый раз, только складываем энергии.
Энергию 2-ой КС Земля у нас заберет за выход 11,2*11,2=
125,
Нам надо чтобы у нас еще осталась энергия на 12,3 км/с =12,3*12,3=
150.
Суммируем эти энергии = 125+150=275. Извлекаем квадратный корень из 275 и получаем скорость 16,58 км/с.
Итого прыгнув со скоростью 16,58 км/с мы убежим не только от Земли, но и от Солнца. Прыгать естественно надо по направлению движения самой Земли, что будет если мы прыгнем в другом направлении мы рассмотрим в следующей статье, пока разберемся с направлениями по/против движения. В этих случаях — нам нужно просто найти скорость вылета относительно Земли и добавить к ней энергию, которую заберет сама Земля за выход.
Кстати, иногда встречается такая идея, почему бы не выбрасывать мусор на Солнце? И в этом примере хорошо видно, что выбросить мусор на Альфа Центавру намного проще, чем на Солнце (если не учитывать орбитальную скорость самих звезд). И чтобы выкинуть мусор из Солнечной системы — его нужно кинуть со скоростью 16,58 км/с, а чтобы скинуть мусор на Солнце — его нужно кинуть со скоростью 11,2*11,2+30*30=
32,02 км/с, тогда после вылета с Земли его скорость относительно Солнца будет равна нулю и он начнет падать на него под прямым углом.
С помощью космических скоростей можно так же легко и быстро посчитать скорость с которой этот мусор упадет на «поверхность» Солнца. Вот давайте её и посчитаем.
Итак, мы прыгаем с Земли
150 млн. км. Сначала посчитаем локальные космические скорости для высоты 150 млн. км.
Изначально, мы двигались с Первой космической скоростью 30 км/с, энергия 30*30=900 (для нашей высоты
150 млн. км), Вторая космическая скорость для этой высоты ровно в 2 раза больше по энергии, значит чтобы вылететь, нужно 1 800 энергии = наша скорость стала равна нулю и теперь нам не хватает 1 800 энергии чтобы вылететь из Солнечной системы.
Теперь считаем максимальную 2-ую КС для «поверхности» Солнца (прыжок с нулевой высоты).
Чтобы выпрыгнуть с поверхности Солнца, нам надо 600 км/с или 360 000 энергии — и до этой энергии нам как раз и не хватает 1 800. И чтобы узнать скорость удара об поверхность нужно из энергии максимальной 2-ой КС вычесть локальную 2-ую КС.
360 000 — 1 800 = 358 200, извлекаем квадратный корень =
598,5 км/с = мусор ударится об «поверхность» Солнца со скоростью 598,5 км/с — почти с максимальной скоростью — мы очень далеко от Солнца.
И тут можно заметить один интересный факт. Помните, я говорил что границу гравитации Земли, обычно округляют до миллиона километров, и для достижения этой высоты потребуется 99,37% энергии от максимальной, остальные 0,63% потеряются за бесконечность.
А вся наша планета двигается со скоростью 30 км/с и её энергия 900 МДж. (на каждые 2 кг), а чтобы вылететь не хватает еще 900 МДж., и это до 360 000 МДж. = нам не хватает всего 0,25% энергии, по сути мы находимся на краю гравитации Солнца, а наша планета — это пыль которой не хватило всего четверть процента энергии, чтобы разлететься по галактике.
Ну и раз пошла такая пьянка, то давайте и 4-ую космическую посчитаем (убегание из галактики), учитывать распределение массы не будем, посчитаем как будто она вся в центре.
По сплетням из Википедии, чтобы свалить из Млечного пути — нужна скорость 550 км/с, само Солнце при этом двигается 217 км/с (округлим до 220).
Итак, нам надо 550 км/с, Солнце уже двигается 220 км/с, 550-220=330 км/с, с этой скоростью нам надо вылететь относительно Солнца. При старте с орбиты Земли, Солнце заберет 900 МДж. энергии за выход, добавляем эту энергию к необходимой скорости.
330*330+900=109 800 МДж.=331,36 км/с — это стартовая скорость с орбиты Земли.
Сама Земля тоже двигается 30 км/с — вычитаем её скорость 331,36-30 = 301,36 км/с — с этой скоростью нам нужно вылететь относительно Земли.
Так же добавляем плату за выход с самой Земли 125,44 МДж.,
301,36*301,36+125=90 943,29 МДж.= 301,57 км/с.
Итого прыгнув с Земли со скоростью 301,57 км/с — мы вылетим из галактики. Правда если любой Рептилоид увидит такой запуск, то он будет очень долго и громко ржать. Как вы наверняка заметили, скорость Солнца складывается со скоростью Земли 220+30=250 км/с, а гравитация забирает не скорость, а энергию — и она вычитается из квадрата скорости. Почему так происходит я подробно расскажу в следующей статье, пока это рассмотрим как факт, и еще нам понадобится факт того, что ракета из 1 кг. топлива всегда получает одно и то же ускорение, например если 1 кг. топлива ускоряет ракету на 10 м/с, то этот же килограмм может ускорить и с 0 до 10 м/с, и со 100 000 до 100 010 м/с (если в 2-х словах, то ракета сжигает=выбрасывает топливо всегда с одной и той же скоростью = получает одинаковое ускорение), а если ракета сможет разогнаться с 0 до 300 км/с, то она сможет разогнаться и с 1 000 до 1 300 км/с, потратив одно и тоже кол-во топлива.
И этим нужно пользоваться. Для этого нужно прыгать не по направлению движения Земли, а против движения.
Но не сразу со скоростью 300 км/с, а сначала
29 км/с, тогда наша скорость относительно Солнца станет 3 км/с и мы начнем «падать» на него — наша орбита станет эллиптической и мы сможем пролететь мимо Солнца на очень близком расстоянии (на любом). И при скорости
3 км/с, мы пролетим около «поверхности» Солнца на расстоянии около 1 метра (чтобы не обжечься сделаем это ночью).
С какой скоростью мы будем пролетать? Ровно с такой же, как если бы мы падали вертикально под прямым углом с начальной скоростью 3 км/с, только при эллиптической орбите — вся эта скорость будет горизонтальной (в точке максимального сближения) и её мы уже считали, это те 598,5 км/с, но там мы сбрасывали мусор и округляли 2-ую космическую Солнца до 600 км/с, а Рептилоиды уважают точность, поэтому возьмем все 617,7 км/с = 381 553 МДж. и «падая» с орбиты Земли, до этой энергии нам не хватит 1 800 — 9 = 1791 МДж, а наша скорость будет 616,24 км/с — и тут мы опять включим двигатели и за 0 секунд ускоримся на 300 км/с — до 916,24 км/с = 839 495 МДж.
Потом Солнце заберет свои 381 553 МДж. и у нас останется 839 495 — 381 553 = 457 942 МДж. = 676,7 км/с. И с этой скоростью мы вылетим за «границу гравитации» Солнца.
На самом деле даже не большое ускорение около Солнца даст огромный выигрыш в скорости, по сути, если на высоте Земли, чтобы «вылететь из гравитации» Солнца нам нужно ускорится на
12,3 км/с, то вблизи Солнца нам нужно ускорится всего на 1,5 км/с, а если мы ускоримся хотя бы на 10 км/с, то скорость вылета «из гравитации» будет 103 км/с. А если сильно заморочиться, то погасить скорость можно намного дешевле, сначала отлететь к Юпитеру, там «развернуться» будет намного дешевле и с учетом старта с Земли можно уложиться в расходы топлива на +20 км/с, и еще на ускорение около Солнца понадобится 10 км/с и тогда можно отправиться к Альфа Центавре со скоростью
100 км/с. Потратив топлива всего на +30 км/с. А в галактике есть звезды и потяжелее Солнца, более того, большинство звездных систем — двойные.
Двойные звезды можно использовать как халявные ускорители и для этого вообще не нужно топливо — нужно орбитальное вращение самих звезд, гравитационные маневры посчитаем в другой раз, просто суть в том, что чем массивнее и быстрее двигается звезда, тем больше ускорения мы можем получить просто пролетая рядом, даже без двигателей.
А пролетая возле белого карлика и ускорившись на 10 км/с, после отлета у нас останется 450 км/с., около Нейтронной звезды эффект будет еще больше, и на самом деле до околосветовых скоростей можно разогнаться с очень небольшим запасом топлива, грамотно пролетев мимо 10-20 звезд, используя топливо только для корректировки курса. Правда времени на такой разгон уйдет…
Да че нам это время:—Время, периоды, масса топлива — всё это для девочек, нам это не интересно — мы будем изучать орбитальную механику с помощью мужицких метров. И для понимания 85% орбитальной механики — нам понадобится всего 1 линия и 2 энергии. Получится очень ограниченная Ньютоновская физика, геометрию будем употреблять не меньше 90 градусов (но и не больше, меру тоже надо знать), всё будет очень просто — максимально оптимизировано для естественных нейронных сетей — минимум параметров, минимум нагрузки на память = максимум производительности. Очень ограниченно, но зато всё это поместится в голове и вы сможете примерно прогнозировать перелеты, к тому же никто не мешает вам открыть учебник геометрии и расширить понимание до полного.
На самом деле, у меня есть один знакомый Рептилоид, и он рассказывал, что у них есть технология, с помощью которой они колонизировали всю свою звездную систему за 100 лет — именно колонизировали, с многотонными и взаимоприбыльными грузоперевозками каждый день (не путать с гробницами для говорящих обезьян). Я долго у него расспрашивал что это за технология, но он сказал что Люди к ней еще не готовы, если дать её 1 человеку и он начнет пользоваться ей первым, то пока все остальные будут понимать что к чему, он уже захватит все планеты и через 50 лет появится вождь Солнечной системы которому будет принадлежать всё, а им нужна сбалансированная конкурентноспособная цивилизация с которой можно договариваться и торговать. Поэтому если все одинаково хорошо будут понимать орбитальную механику, то он обещал подумать насчет передачи этой технологии. Так что обязательно подписывайтесь на мой канал (на Хабре это не просто, но никто не говорил что будет легко).
В следующей статье, я расскажу об энергии и импульсе.
Возможно вы заметили «парадокс», что скорости складываются линейно, а энергия вычитается квадратично и откуда берется эта гигантская разница в скорости вылета — вот в следующей статье я и расскажу, почему никакого парадокса там нет.
У меня был другой аккаунт с миллионами просмотров, но я забыл от него пароль. И среди миллионов подписчиков, там была Лена и ей очень нравились мои научно популярные статьи, она всегда смеялась над моими шутками… У неё очень приятный голос, красивые волосы и вообще она очень добрая и отзывчивая — и всегда всем помогает, а люди этого не ценят. И она очень просила меня написать статью про вторую космическую скорость — а я ей пообещал. Но я забыл пароль от того аккаунта, который приносил миллионную прибыль, да черт с ними — с деньгами, самое ужасное, что Лена сейчас сидит… и ждет — когда же выйдет статья про космические скорости? А она никогда не выйдет на том аккаунте — потому что я… забыл… пароль…
Наверно она сейчас сидит… жмет F5 и ждёт – ну когда же появится статья про космические скорости. Господи, неужели она никогда не найдет мой новый аккаунт. А я если честно писал эту статью только ради неё. Неужели она никогда не узнает про космические скорости, а еще, я столько ей наобещал — и про электромагнитную хунту, и про прОклятый логарифм, и про гравитационные маневры. Даже страшно представить, что сейчас с ней происходит. Мне очень стыдно вас просить, потому что я сам во всём виноват, но если вам не трудно, то сделайте пожалуйста репост этой статьи во всех своих социальных сетях — возможно у вас в друзьях есть та самая Лена — и она увидит эту статью про космические скорости и найдет мой новый аккаунт.
Иногда, между состояниями ни жив ни мертв — я коллапсирую на твиче.