для чего нужны прямоугольные координаты

Активный туризм на Юге России

1.10. ПРЯМОУГОЛЬНЫЕ КООРДИНАТЫ НА КАРТАХ

Рис. 14. Прямоугольные координаты

В топографии и геодезии, а также на топографических картах ориентирование производится по северу со счетом углов по ходу часовой стрелки, поэтому для сохранения знаков тригонометрических функций положение осей координат, принятое в математике, повернуто на 90°.

Прямоугольные координаты на топографических картах СССР применяются по координатным зонам. Координатные зоны — части земной поверхности, ограниченные меридианами с долготой, кратной 6°. Первая зона ограничена меридианами 0° и 6°, вторая—б» и 12°, третья—12° и 18° и т.д.

Счет зон идет от Гринвичского меридиана с запада на восток. Территория СССР располагается в 29 зонах: от 4-й до 32-й включительно. Протяженность каждой зоны с севера на юг порядка 20000 км. Ширина зоны на экваторе около 670 км, на широте 40°— 510 км, т широте 50°—430 км, на широте 60°—340 км.

Все топографические карты в пределах данной зоны имеют общую систему прямоугольных координат. Началом координат в каждой зоне служит точка пересечения среднего (осевого) меридиана зоны с экватором (рис. 15), средний меридиан зоны соответствует

Рис. 15. Система прямоугольных координат на топографических картах: а—одной зоны; б—части зоны

Зависимость между условными координатами и их действительными значениями выражается формулами:

X ‘ = Х-, У = У— 500 000,

Х = 5 650 450: Y = 3 620 840,

то это значит, что точка расположена в третьей зоне на удалении 120 км 840 м от среднего меридиана зоны (620840—500000) и к северу от экватора на удалении 5650 км 450 м.

Полные координаты — прямоугольные координаты, записанные (названные) полностью, без каких-либо сокращений. В примере, приведенном выше, даны полные координаты объекта:

Х = 5 650 450; Y = 3620 840.

Сокращенные координаты применяются для ускорения целеука-зания по топографической карте, в этом случае указываются только десятки и единицы километров и метры. Например, сокращенные координаты данного объекта будут:

Х = 50 450; Y = 20 840.

Сокращенные координаты нельзя применять при целеуказании на стыке координатных зон и если район действий охватывает пространство протяженностью более 100 км по широте или долготе.

Координатная (километровая) сетка —сетка квадратов на топографических картах, образованная горизонтальными и вертикальными линиями, проведенными параллельно осям прямоугольных координат через определенные интервалы (табл. 5). Эти линии называются километровыми. Координатная сетка предназначается для определения координат объектов и нанесения на карту объек тов по их координатам, для целеуказания, ориентирования карты, измерения дирекционных углов и для приближенного определения расстояний и площадей.

Источник

Системы координат. Определение географических и прямоугольных координат.

Координатами называются угловые или линейные вели­чины, определяющие положение точек на какой-либо поверхности или в пространстве.

Существует много различных систем координат. Для опреде­ления положения точек на земной поверхности применяются глав­ным образом географические, плоские прямоугольные и полярные координаты.

1. Географические координаты.Географическими координа­тами называются угловые величины — широта и долгота, опреде­ляющие положение точек на земном шаре.

Географической широтой называется угол между от­весной линией в данной точке земной поверхности и плоскостью экватора. Широту принято обозначать греческой буквой φ (фи). Очевидно, что для любой точки М на поверхности шара (рис. 47) угол MCN будет широтой этой точки. Широты отсчитываются по дуге меридиана в обе стороны от экватора, начиная с 0° до 90°. В северном полушарии широты считаются северными, а в юж­ном — южными.

Все точки, лежащие на одной географической парал­лели, имеют одинаковую ши­роту, поэтому одна широта еще не определяет положения точки на земной поверхности, Необходимо знать вторую ко­ординату — долготу.

Географической дол­готой называется угол между плоскостью меридиана данной точки и плоскостью ме­ридиана, условно принятого за начальный. Географиче­скую долготу обычно обозна­чают греческой буквой λ (ламбда). Угол OCN (рис. 6) будет долготой точки М. У нас за начальный принят Гринвичский меридиан. Долготы отсчитываются по дуге эква­тора или параллели в обе стороны от начального меридиана, на­чиная с 0° до 180°. Долготы к востоку от начального меридиана до 180° называются восточными, а к западу — западными. Все точки, лежащие на одном меридиане, имеют одинаковую долготу.

Разность долгот двух пунктов показывает не только их взаим­ное расположение, но и разницу во времени в этих пунктах в один и тот же момент: каждые 15° по долготе соответ­ствуют одному часу времени. Например, долгота г.Москва 37°37′ (восточная), а г.Хабаровск 135°05′, т. е. по­следний лежит восточнее на 97°28′. Таким образом, когда в Мос­кве полдень (13 часов), в Хабаровске 19 часов 30 минут (по пояс­ному времени 20 часов).

Рис. 6. Географические координаты

Определение географических координат по карте. На (рис.7) показано оформление рамок листов топографических карт. Как видно из рисунка, в углах рамки карты подписаны долготы меридианов и широты параллелей, образующих стороны этой рамки. Между внутренней и внешней рамками нанесена шкала, разбитая на минуты широты (по боковым сторонам рамки) и долготы (по верхней и нижней сторонам рамки).

Таким образом, чтобы определить широту какой-либо точки А на карте (рис. 7), надо через эту точку провести параллель, т. е. прямую, соединяющую одноименные деления (или их доли) па шкалах минут западной и восточной сторон рамки, а затем по одной из этих шкал отсчитать широту параллели. Это и будет ши­рота определяемой точки А. Проводить при этом параллель через весь лист карты не требуется, а нужно лишь отметить наколом циркуля или коротким штрихом точку ее пересечения со шкалой минут, по которой будет производиться отсчет широты. Для отсчета широты надо сосчитать по шкале, сколько минут заключается между южной стороной рамки карты и параллелью определяемой точки, и полученное число минут прибавить к широте южной стороны рамки.

Рис. 7. Оформление рамки листа топографической карты (масштаба1 :100 000)

Аналогично, пользуясь шкалами минут северной и южной сторон рамки карты, определяют и долготу точки. На (рис. 7) широта точки А будет 54°58′,6, а долгота 37°31′,0 (восточная).

Для точного определения географических координат по карте необходимо иметь линейку длиной не менее 40 см.

На картах последних лет издания минуты на шкалах широт и долгот дополнительно разбиты точками на 10-секундные деления, что позволяет определять географические координаты с точностью порядка 3-4« (см. рис. 7).

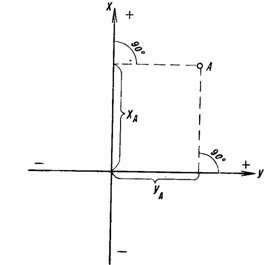
2. Плоские прямоугольные координаты. Плоскими прямоугольными координатами называются линейные величины — абсцисса и ордината, определяющие положение точек на плоскости.

Две взаимно перпендикулярные прямые X и Y, относительно которых определяется положение точек (рис. 8), называются осями координат; из них ось X называется осью абсцисс, а ось Y — осью ординат. Точка пересечения осей — точка О — называется началом координат.

Оси координат делят плоскость на четыре четверти, счет которых ведется в топографии по ходу часовой стрелки от положительного направления оси Х. Заположительное направление осей координат принимается для оси абсцисс (X) направление на севep, а для оси ординат (У) — на восток.

Положение любой точки М на плоскости относительно начала координат О (рис. 8) определяется кратчайшими расстояниями до нее от осей координат, измеренными в каких-либо мерах длины, например в метрах. Эти расстояния, являющиеся координатами точек, изобразятся, очевидно, отрезками прямых линий, перпендикулярных к одной из координатных осей и параллельных другой.

Координата X— абсцисса — вверх от оси Y считается положительной, а вниз от нее — отрицательной.

Координата Y — ордината — вправо от оси Y считается положительной, а влево от нее — отрицательной.

Таким образом, точки на (рис. 8) будут иметь следующие координаты:

Рис. 8. Прямоугольные координаты

Использование координатной сетки при работе на карте.Координатная сетка весьма широко используется при работе на карте. Основное ее назначение — облегчить и упростить определение прямоугольных координат точек местности при целеуказании по карте. Вместе с тем она облегчает ориентирование на карте и указание на ней местоположения различных объектов при докладах, постановке задач, передаче распоряжений и составлении донесений. Наконец, она помогает быстро оценивать по карте на глаз расстояния и определять азимуты направлений.

Приближенное указание объектов и ориентирование на карте.Чтобы указать приближенно местоположение какого-нибудь пункта на карте, достаточно назвать квадрат сетки, в котором он расположен. Для этого надо прочитать за рамкой карты оцифровку вертикальной и горизонтальной километровых линий, образующих нижний левый (юго-западный) угол квадрата. При этом не обходимо обязательно соблюдать следующее правило: сначала прочитывать и называть оцифровку (номер) горизонтальной километровой линии, а затем вертикальной, т. е. сначала называть абсциссу X, потом ординату Y.

Например, командир, ориентирующий по карте своих подчиненных в обстановке, указывая местоположение точки с отметкой 118,0 (рис. 9), скажет: «Квадрат сорок, сорок два: высота с отметкой 118,0». В письменных же донесениях и других документах этот пункт будет обозначаться так: «Высота с отметкой 118,0 (4042)».

Рис. 9. Обозначение дополнительной сетки за рамкой карты

Для получения ординаты Y записывают левую (вертикальную) сторону того же квадрата (т.е. 77) и затем приписывают X ней расстояние в метрах, измеренное от нее по перпендикуляру до определяемой точки, т. е. отрезок п (750 м).

Таким образом, в данном примере координаты точки М будут:

Х =36 330 м; Υ= 77 750 м.

Так как в данном случае при определении координат точки М цифровое обозначение километровых линий было записано неполностью, а лишь последними двумя их цифрами (36 и 77), то такие координаты называют сокращенными координатами точки М. В таком виде координаты обычно и записываются при определении их по карте.

Рис. 10. Определение по карте прямоуголь­ных координат цели

Если же оцифровку километровых линий записывать полностью, то получим полные координаты, как они обычно записываются в специальных списках (каталогах) координат геодезических пунктов. В нашем примере (рис. 57) полные координаты точки М запишутся так:

Χ = 6 136 330 м; Υ = 5 577 750 м.

Измерение координат точек по карте и нанесение точек на карту по координатам производятся обычным способом, применяемым при измерении и откладывании прямых отрезков по масштабу карты, т. е. с помощью циркуля, или же по линейке с миллиметровыми делениями. Для этой же цели могут применяться специальные координатомеры, которые несколько упро­щают работу, заменяя при этом масштаб, циркуль и линейку. На (рис. 10) показан простейший координатомер, который легко изготовить самому из картона или пластика. Оцифровка координатомера и пользование им ясны из рисунка.

Точность определения по карте прямоугольных координат точек ограничивается не только ее масштабом, но и величиной погрешностей, допускаемых при съемке или составлении карты в нанесении на нее различных точек и объектов местности. Наиболее точно — с ошибкой, не превышающей 0,2 мм,— на карту наносятся геодезические пункты и наиболее резко выделяющиеся на местности и видимые издали предметы, имеющие значение ориентиров и определяемые как геодезические пункты (отдельные колокольни, фабричные трубы, постройки башенного типа). Поэтому координаты таких точек возможно определять по карте примерно с той же точностью, с какой они на нее наносятся (т. е. с ошибкой 10—15 м для карты масштаба 1 :50000 и 20—30 м для карты масштаба 1 : 100 000).

Остальные ориентиры и точки контуров наносятся на карту, а следовательно, и определяются по ней с ошибкой до 0,5 мм, а точки, относящиеся к нечетко выраженным на местности контурам (например, контуру болота),— с ошибкой до 1 мм.

Нанесение на карту точки по координатам.Разберем это на примере (рис. 11). Допустим, требуется с помощью координатомера нанести на карту обнаруженную цель М, координаты которой

Χ= 65450 м; Υ = 90 850 м.

Первые две цифры координат указывают, что цель находится в квадрате, у которого нижняя сторона имеет значение 65, а левая 90. Накладываем на этот квадрат координатомер так, чтобы одна из его шкал совпала с нижней стороной квадрата и нуль шкалы был справа. Передвигаем координатомер вдоль горизонтальной стороны квадрата до тех пор, пока против левой его стороны не придется деление шкалы с отсчетом 850 м. После этого против отсчета 450 м на вертикальной шкале координатомера накалываем точку М.

Рис. 11. Нанесение на карту целей по прямоуголь­ным координатам

Источник

Прямоугольная система координат. Ось абсцисс и ординат

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат (в правом нижнем углу экрана).

Прямоугольная декартова система координат

Французский математик Рене Декарт преддложил вместо геометрических построений использовать математические расчеты. Так появился метод координат, о котором мы сейчас расскажем.

Координаты — это совокупность чисел, которые определяют положение какого-либо объекта на прямой, плоскости, поверхности или в пространстве. Например, координаты школы тоже можно записать числами — они помогут понять, где именно находится наша школа. С точками на плоскости та же история.

Координатой можно назвать номер столика в кафе, широту и долготу на географической карте, положение точки на числовой оси и даже номер телефона друга. Проще говоря, когда мы обозначаем какой-то объект набором букв, чисел или других символов, тем самым мы задаем его координаты.

Прямоугольная система координат — это система координат, которую изобрел математик Рене Декарт, ее еще называют «декартова система координат». Она представляет собой два взаимно перпендикулярных луча с началом отсчета в точке их пересечения.

Чтобы найти координаты, нужны ориентиры, от которых будет идти отсчет. На плоскости в этой роли выступят две числовые оси.

Чертеж начинается с горизонтальной оси, которая называется осью абсцисс и обозначается латинской буквой x (икс). Записывают ось так: Ox. Положительное направление оси абсцисс обозначается стрелкой слева направо.

Затем проводят вертикальную ось, которая называется осью ординат и обозначается y (игрек). Записывают ось Oy. Положительное направление оси ординат показываем стрелкой снизу вверх.

Оси взаимно перпендикулярны, а значит угол между ними равен 90°. Точка пересечения является началом отсчета для каждой из осей и обозначается так: O. Начало координат делит оси на две части: положительную и отрицательную.

Единичные отрезки располагаются справа и слева от оси Oy, вверх и вниз от оси Oy. Числовые значения на оси Oy располагаются слева или справа, на оси Ox — внизу под ней. Чаще всего единичные отрезки двух осей соответствуют друг другу, но бывают задачи, где они не равны.

Оси координат делят плоскость на четыре угла — четыре координатные четверти.

У каждой из координатных четвертей есть свой номер и обозначение в виде римской цифры. Отсчет идет против часовой стрелки:

Чтобы узнать координаты точки в прямоугольной системе координат, нужно опустить от точки перпендикуляр на каждую ось и посчитать количество единичных отрезков от нулевой отметки до опущенного перпендикуляра. Координаты записывают в скобках, первая по оси Ох, вторая по оси Оу.

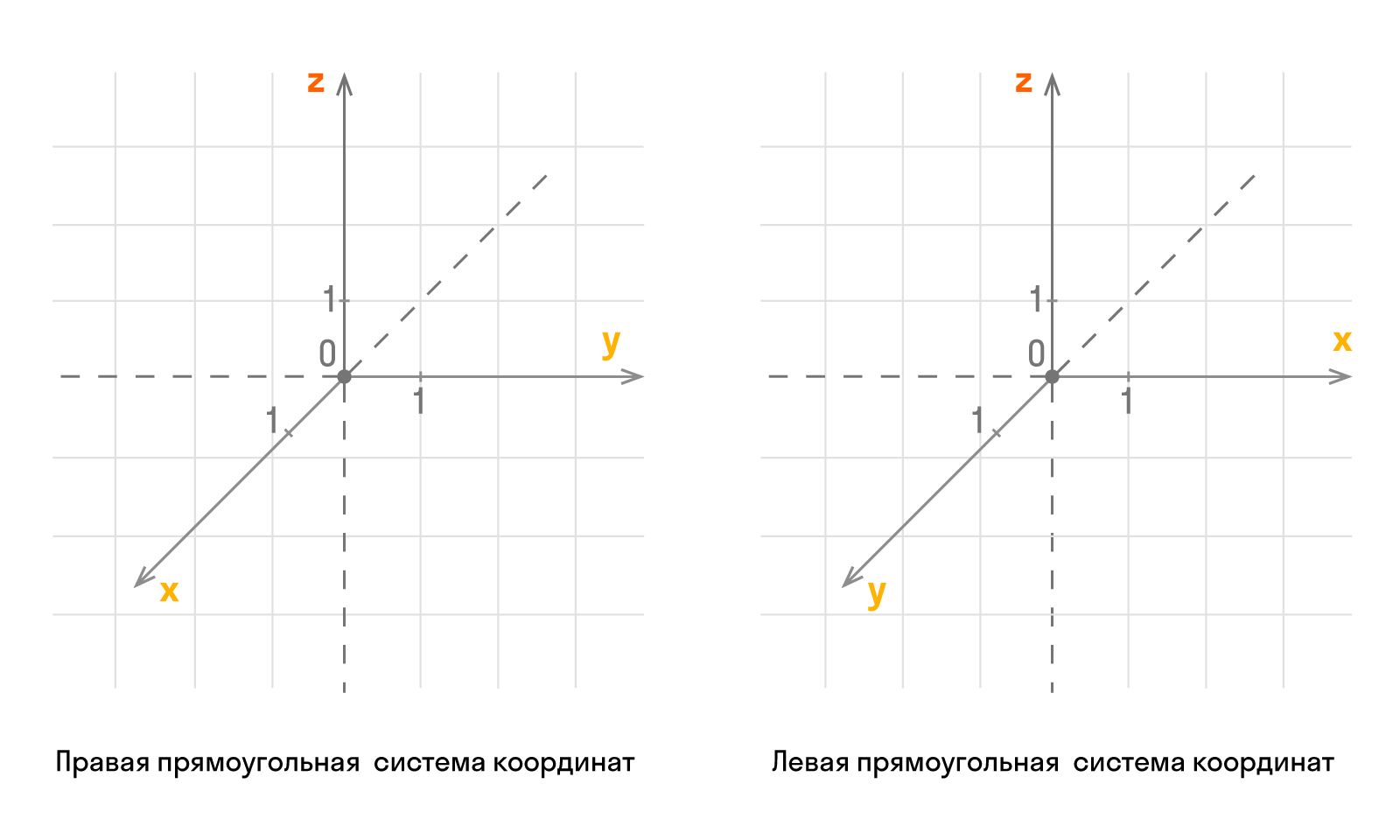
Прямоугольная система координат в трехмерном пространстве

Трехмерное евклидово пространство состоит из трех взаимно перпендикулярных прямых: Ох, Оу, Оz, где Оz — ось аппликат. По направлению координатных осей есть разделение на правую и левую прямоугольные системы координат трехмерного пространства.

Оси координат пересекаются в точке О, которую называют началом. У каждой оси есть положительное направление, которое отмечается стрелкой. Если при повороте Ох против часовой стрелки на 90° ее положительное направление совпадает с положительным Оу, тогда это применимо для положительного направления Оz. Такую систему считают правой. Объясняем на пальцах! Если сравнить направление Х с большим пальцем руки, то указательный отвечает за Y, а средний за Z.

Также образуется левая система координат. Совмещать обе системы нет смысла, так как соответствующие оси не совпадут.

Координаты точки в декартовой системе координат

Для начала отложим точку М на координатной оси Ох. Любое действительное число x_M равно единственной точке М, которая располагается на данной прямой. При этом начало отсчета координатных прямых всегда ноль.

Каждая точка М, которая расположена на Ох, равна действительному числу x_M. Этим действительным числом и является ноль, если точка М расположена в начале координат, то есть на пересечении Оx и Оу. Если точка удалена в положительном направлении, то число длины отрезка положительно и наоборот.

Число x_M — это координата точки М на заданной координатной прямой.

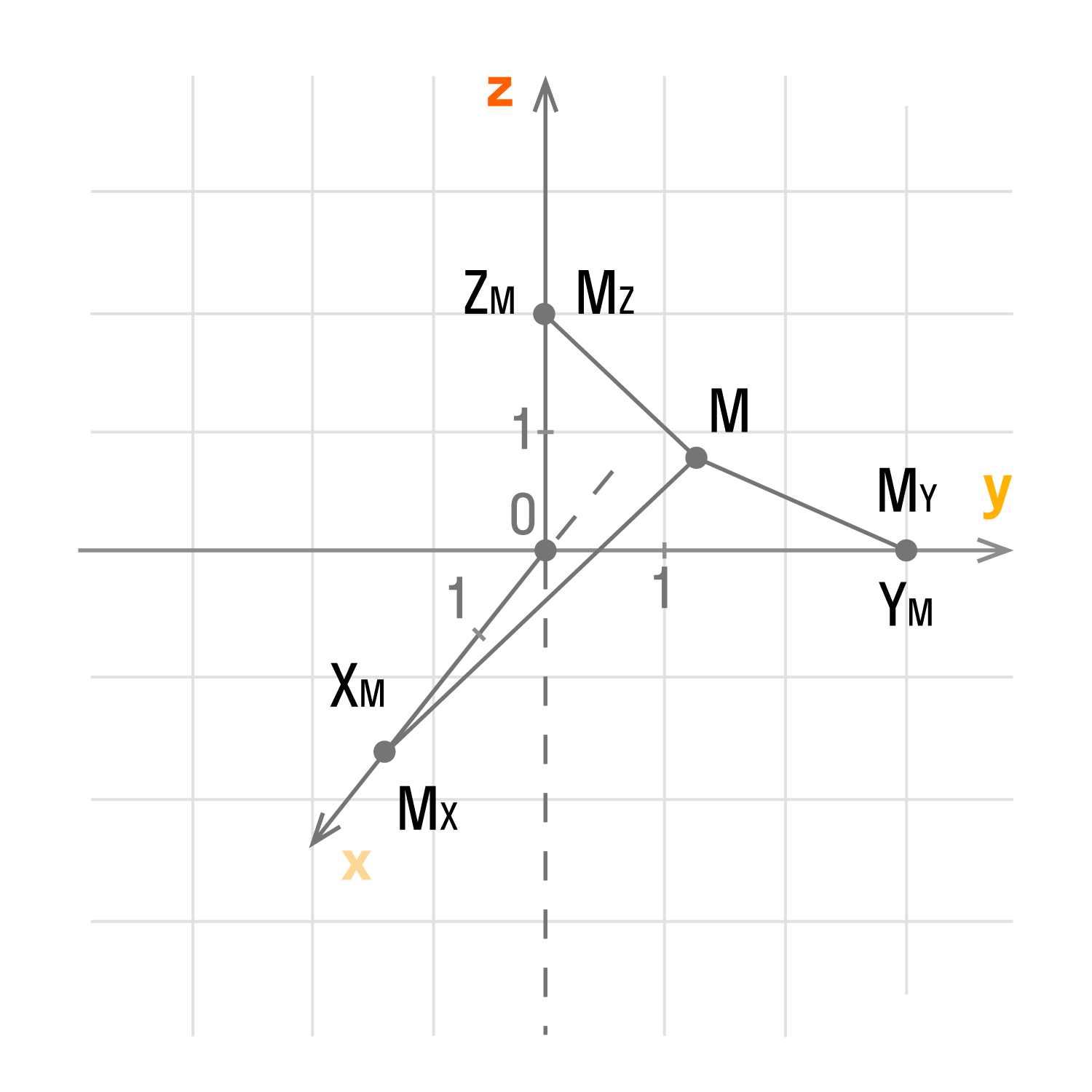
Пусть точка будет проекцией точки M_x на Ох, а M_y на Оу. Значит, через точку М можно провести перпендикулярные осям Оx и Оу прямые, после чего получим соответственные точки пересечения M_x и M_y.Тогда у точки M_x на оси Оx есть соответствующее число x_M, а M_y на Оу — y_M. Как это выглядит на координатных осях:

Каждой точке М на заданной плоскости в прямоугольной декартовой системе координат соответствует пара чисел (x_M, y_M), которые называются ее координатами. Абсцисса М — это x_M, ордината М — это y_M.

Обратное утверждение тоже верно: каждая пара (x_M, y_M) имеет соответствующую точку на плоскости.

Координаты точки в трехмерном пространстве

Сформулируем определение точки М в трехмерном пространстве.

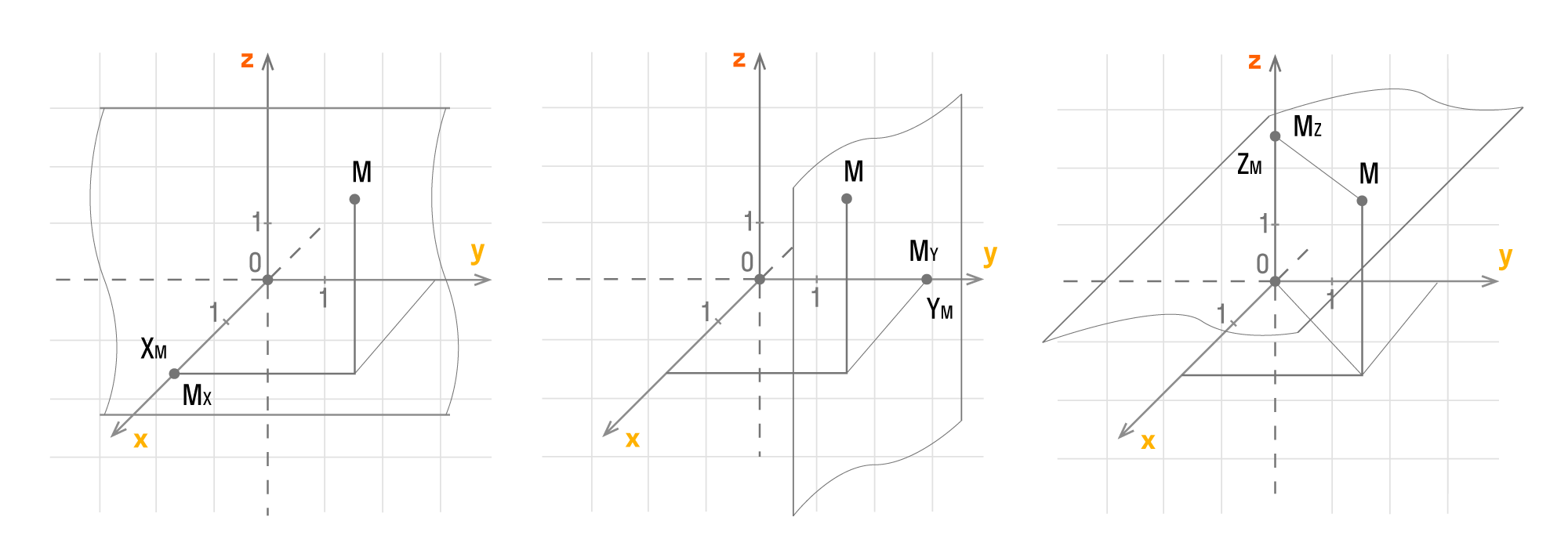
Пусть M_x, M_y, M_z — это проекции точки М на соответствующие оси Оx, Оy, Оz. Тогда значения этих точек на осях примут значения x_M, y_M, z_M. Как это выглядит на координатных прямых:

Чтобы получить проекции точки М, нужно добавить перпендикулярные прямые Оx, Оy, Оz, продолжить их и изобразить в виде плоскостей, которые проходят через М. Так плоскости пересекутся в M_x, M_y, M_z.

У каждой точки трехмерного пространства есть свои данные (x_M, y_M, z_M), которые являются координатами точки М.

x_M, y_M, z_M — это числа, которые являются абсциссой, ординатой и аппликатой данной точки М. Верно и обратное утверждение: каждая упорядоченная тройка действительных чисел (x_M, y_M, z_M) в заданной прямоугольной системе координат имеет одну соответствующую точку М трехмерного пространства.

Источник

Плоские прямоугольные координаты, как определить плоские прямоугольные координаты по топографической карте.

Линии параллелей и меридианов, которые служат рамкой для данного листа бумажнойтопографической карты, представляют собой кривые линии, хотя кривизна их в пределах одного листа практически и незаметна. Но в пределах каждой зоны Гаусса имеются две линии, которые изображаются на карте прямыми линиями. Это осевой меридиан зоны и экватор. Эти две линии приняты за оси плоских прямоугольных координат и определяют сами плоские прямоугольные координаты.

Плоские прямоугольные координаты, как определить плоские прямоугольные координаты по топографической карте.

Линию осевого меридиана считают осью абсцисс и обозначают х, линию экватора — осью ординат и обозначают у. За начало координат принимают точку пересечения осевого меридиана с экватором. Таким ебразом, в каждой зонеГаусса имеется своя сетка плоских прямоугольных координат. Координаты х (абсциссы) отсчитываются к северу и югу от экватора, то есть от 0 (на экваторе) до 10 000 км (на полюсе).

К северу от экватора координата у считается положительной, к югу — отрицательной. Координаты ху (ординаты) отсчитываются от осевого меридиана вправо (к востоку) и влево (к западу). Чтобы не иметь дела с отрицательными значениями для этих координат, условились значение ординаты у для осевого меридиана принимать равным 500 км.

Тем самым ось х как бы переносится к западу на 500 км и все значения ординат в пределах данной зоны будут иметь всегда положительный знак. Кроме того, к значению ординаты у спереди всегда приписывается цифра, соответствующая номеру зоны Гаусса для того, чтобы избежать повторения координат, расположенных в разных зонах.

Как определить плоские прямоугольные координаты по топографической карте.

Чтобы можно было определить плоские прямоугольные координаты точек в каждой зоне Гаусса на топографическихкартах наносится прямоугольная сетка координат, то есть проводятся линии, параллельные осевому меридиану и экватору.

Эти прямые линии, естественно, не будут совпадать с линиями, изображающими меридианы и параллели. За исключением осевого меридиана и экватора, параллельно которым они проводятся. Эту сетку координат называют километровой, так как ее линии проводятся через километр длямасштабов 1:10 000, 1:25 000, 1:50 000.

На каждом листе карты вдоль внутренней рамки даются значения координат километровой сетки от осевого меридиана данной зоны и от экватора. Значения полных координат подписываются только у крайних (верхней и нижней) линии сетки координат. У всех же промежуточных линий подписываются сокращенные обозначения, то есть только последние две цифры (десятки и единицы километров).

Например, нижняя линия километровой сетки на рисунке имеет обозначение 5042, а следующая над ней линия сетки обозначена только цифрой 43 км, а не 5043. Цифры километровой сетки под южной и над северной рамкой листа карты обозначают ординаты (у) этих линий. Крайние линии также обозначены полными координатами. Но в отличие от горизонтальных линий, первая цифра у ординат обозначает номер зоны.

Например, ордината у = 8384 км. Это значит, что лист данной карты расположен в восьмой шестиградусной зоне Гаусса, то есть ограниченной 42 и 48 меридианами восточной долготы, а точки, лежащие на линии у = 384, расположены слева от осевого меридиана на расстоянии 500-384=116 км.

С помощью километровой сетки координат можно, не прибегая к дополнительным измерениям, определить плоские прямоугольные координаты любойточки на карте. С точностью до километра. Для этого достаточно найти, в каком квадрате сетки находится определяемая точка М, и прочитать цифры, обозначающие данный квадрат. Сначала обычно называется (записывается) значение координаты х — 5044, а затем у = 8384.

Указание какого-либо объекта на топографической карте с помощью плоских прямоугольных координат.

Для указания какого-либообъекта на карте обычно говорят так: точка М находится в квадрате 50 448 384, то есть называют координаты ее подряд, не разделяя их, но чаще дают указания сокращенно, называют только две последующие цифры из плоских прямоугольных координат данной точки — квадрат 4484.

Называя этот квадрат на карте, мы указываем координаты левого нижнего его угла. То есть юго-западного угла квадрата, в котором расположена точка М. Если необходимо указать более точное положение точки внутри этого квадрата, то дополнительно определяют ее расстояние от граничных линий этого квадрата. Используя масштаб, переводят эти расстояния в метры и приписывают их к цифрам обозначенного квадрата.

Например, точка М имеет следующие координаты: х = 44 500 метров, а у = 84 500 метров. Это и будут сокращенные координаты для точки М, а полные плоские прямоугольные координаты для нее запишутся так: х = 5 044 500 м, у — 384 500 м.

Нанесение точек на карту по известным плоским прямоугольным координатам производится в обратной последовательности. Сначала отбрасываются три последние цифры в координатах и находятся линии километровой сетки. То есть квадрат, в котором расположена точка. Затем, с помощьюлинейки, масштаба и циркуля, наносятся точные координаты данной точки в этом квадрате.

Две сетки плоских прямоугольных координат на топографических картах.

На некоторых топографических картах можно встретить две сетки плоских прямоугольных координат. Одна нанесена полностью так, как это было показано на рисунке выше. Вторая обозначена только за рамкой данной карты. В чем тут дело? Мы уже ранее установили, что вертикальные километровые линии параллельны осевому меридиану своей зоны, а осевые меридианы соседних зон между собой не параллельны.

Следовательно, при стыковке километровых сеток двух соседних зон линии одной из них располагаются под углом к линиям другой. Вследствие этого на стыке двух зон могут возникнуть затруднения вопределении координат, так как они будут относиться к разным осям координат.

Чтобы устранить это неудобство, в каждой шестиградусной зоне все листы карт, расположенные в пределах 2 градусов к востоку и 2 градусов к западу от границы зоны имеют помимо своей координатной сетки еще и дополнительную, являющуюся продолжением координатной сетки соседней зоны.

И для того чтобы не затемнять второй сеткой данные листы карты, ее обозначают лишь цифрами на внешней рамке листа. Цифры эти являются продолжением нумерации линий координатной сетки смежной зоны.

По материалам книги «Карта и компас мои друзья».
Клименко А.И.

Источник