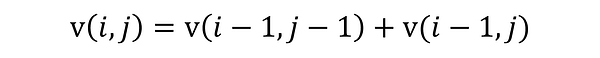для чего нужны рекурсивные функции
Рекурсия. Занимательные задачки
В этой статье речь пойдет о задачах на рекурсию и о том как их решать.
Кратко о рекурсии
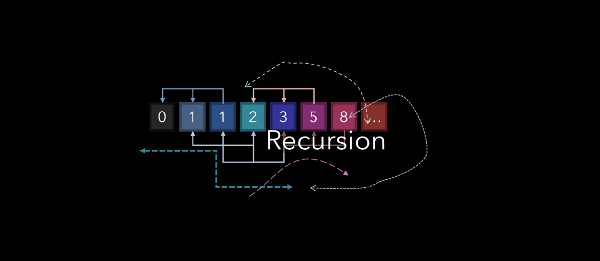
Рекурсия достаточно распространённое явление, которое встречается не только в областях науки, но и в повседневной жизни. Например, эффект Дросте, треугольник Серпинского и т. д. Один из вариантов увидеть рекурсию – это навести Web-камеру на экран монитора компьютера, естественно, предварительно её включив. Таким образом, камера будет записывать изображение экрана компьютера, и выводить его же на этот экран, получится что-то вроде замкнутого цикла. В итоге мы будем наблюдать нечто похожее на тоннель.
В программировании рекурсия тесно связана с функциями, точнее именно благодаря функциям в программировании существует такое понятие как рекурсия или рекурсивная функция. Простыми словами, рекурсия – определение части функции (метода) через саму себя, то есть это функция, которая вызывает саму себя, непосредственно (в своём теле) или косвенно (через другую функцию).
Задачи
При изучении рекурсии наиболее эффективным для понимания рекурсии является решение задач.
Любой алгоритм, реализованный в рекурсивной форме, может быть переписан в итерационном виде и наоборот. Останется вопрос, надо ли это, и насколько это будет это эффективно.
Для обоснования можно привести такие доводы.
Для начала можно вспомнить определение рекурсии и итерации. Рекурсия — это такой способ организации обработки данных, при котором программа вызывает сама себя непосредственно, либо с помощью других программ. Итерация — это способ организации обработки данных, при котором определенные действия повторяются многократно, не приводя при этом к рекурсивным вызовам программ.
После чего можно сделать вывод, что они взаимно заменимы, но не всегда с одинаковыми затратами по ресурсам и скорости. Для обоснования можно привести такой пример: имеется функция, в которой для организации некого алгоритма имеется цикл, выполняющий последовательность действий в зависимости от текущего значения счетчика (может от него и не зависеть). Раз имеется цикл, значит, в теле повторяется последовательность действий — итерации цикла. Можно вынести операции в отдельную подпрограмму и передавать ей значение счетчика, если таковое есть. По завершению выполнения подпрограммы мы проверяем условия выполнения цикла, и если оно верно, переходим к новому вызову подпрограммы, если ложно — завершаем выполнение. Т.к. все содержание цикла мы поместили в подпрограмму, значит, условие на выполнение цикла помещено также в подпрограмму, и получить его можно через возвращающее значение функции, параметры передающееся по ссылке или указателю в подпрограмму, а также глобальные переменные. Далее легко показать, что вызов данной подпрограммы из цикла легко переделать на вызов, или не вызов (возврата значения или просто завершения работы) подпрограммы из нее самой, руководствуясь какими-либо условиями (теми, что раньше были в условии цикла). Теперь, если посмотреть на нашу абстрактную программу, она примерно выглядит как передача значений подпрограмме и их использование, которые изменит подпрограмма по завершению, т.е. мы заменили итеративный цикл на рекурсивный вызов подпрограммы для решения данного алгоритма.
Задача по приведению рекурсии к итеративному подходу симметрична.
Подводя итог, можно выразить такие мысли: для каждого подхода существует свой класс задач, который определяется по конкретным требованиям к конкретной задаче.
Более подробно с этим можно познакомиться тут
Так же как и у перебора (цикла) у рекурсии должно быть условие остановки — Базовый случай (иначе также как и цикл рекурсия будет работать вечно — infinite). Это условие и является тем случаем к которому рекурсия идет (шаг рекурсии). При каждом шаге вызывается рекурсивная функция до тех пор пока при следующем вызове не сработает базовое условие и произойдет остановка рекурсии(а точнее возврат к последнему вызову функции). Всё решение сводится к решению базового случая. В случае, когда рекурсивная функция вызывается для решения сложной задачи (не базового случая) выполняется некоторое количество рекурсивных вызовов или шагов, с целью сведения задачи к более простой. И так до тех пор пока не получим базовое решение.
Тут Базовым условием является условие когда n=1. Так как мы знаем что 1!=1 и для вычисления 1! нам ни чего не нужно. Чтобы вычислить 2! мы можем использовать 1!, т.е. 2!=1!*2. Чтобы вычислить 3! нам нужно 2!*3… Чтобы вычислить n! нам нужно (n-1)!*n. Это и является шагом рекурсии. Иными словами, чтобы получить значение факториала от числа n, достаточно умножить на n значение факториала от предыдущего числа.
В сети при обьяснении рекурсии также даются задачи нахождения чисел Фибоначчи и Ханойская башня
Рассмотрим же теперь задачи с различным уровнем сложности.
Попробуйте их решить самостоятельно используя метод описанный выше. При решении попробуйте думать рекурсивно. Какой базовый случай в задаче? Какой Шаг рекурсии или рекурсивное условие?
Поехали! Решения задач предоставлены на языке Java.
A: От 1 до n
Дано натуральное число n. Выведите все числа от 1 до n.
Продвинутый взгляд на рекурсию
Рекурсия является одним из наиболее мощных подходов в программировании. С ее помощью можно решать чрезвычайно сложные задачи, печатая при этом невероятно малый объем кода. Тем не менее понимание данного принципа нередко вызывает сложности, поскольку для этого требуется нестандартный взгляд на процесс выполнения команд.
Сложность примеров, описанных в данной статье, будет возрастать постепенно, начиная от самых простых и заканчивая достаточно трудными. При этом каждый из них будет сопровождаться подробной диаграммой:
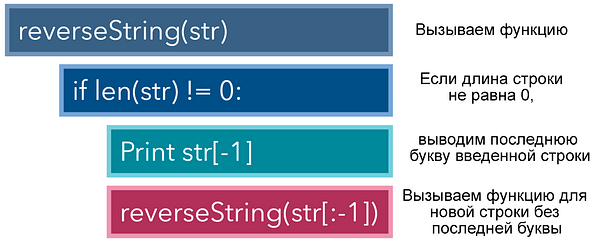
Рекурсия используется для решения задач, в которых функция вызывает сама себя в рамках собственного определения. В каждой реализации рекурсии должно присутствовать два элемента:
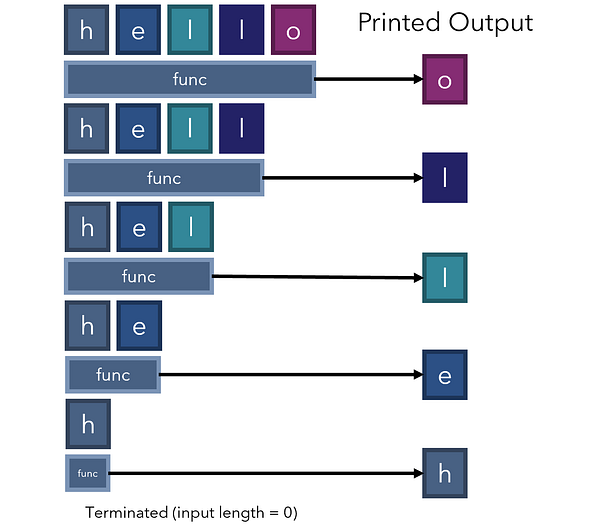
В качестве примера давайте рассмотрим задачу по выводу развернутого варианта строки. В этом случае на выходе из вводного слова ‘hello’ должно получиться ‘olleh’. Итеративный метод решения этой задачи — применение цикла for и вывод каждого знака, начиная с последнего и заканчивая первым.
Давайте посмотрим, как эта рекурсивная функция работает с ‘hello’:
Рекуррентность в более сложных задачах может вызвать трудности при определении двух ее компонентов — рекуррентного соотношения, т.е. соотношения между результатом задачи и результатом ее подзадач и базовым кейсом, представляющим кейс, который можно вычислить напрямую без дополнительных рекурсивных вызовов. Иногда базовые кейсы называются “нижними кейсами”, потому что они являются кейсами, в которых задача уменьшена до наименьшего масштаба.
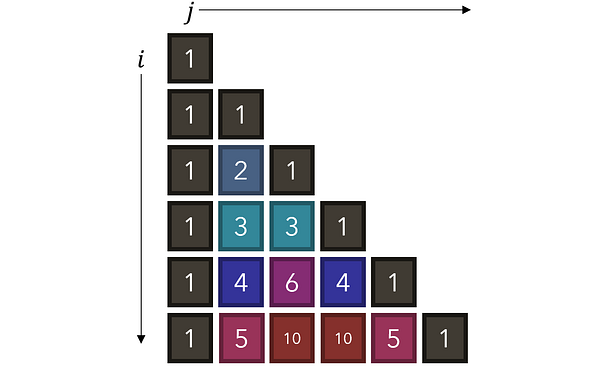
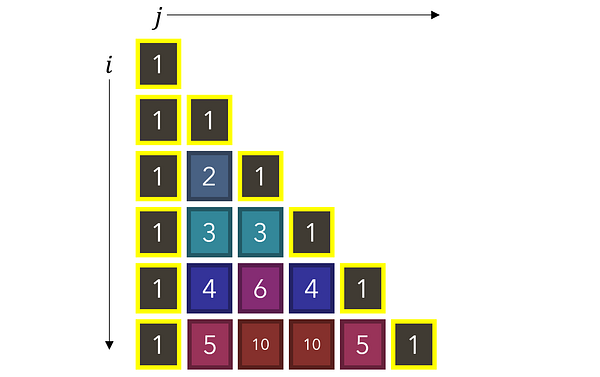
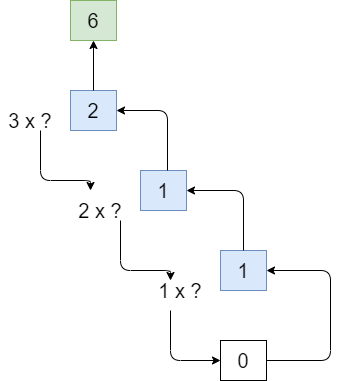
Рассмотрите в качестве примера треугольник Паскаля, в котором каждое число является суммой двух, находящихся над ним, и который имеет по сторонам единицы. Как можно использовать рекурсию для нахождения значения любого значения в точке (i, j)? Каково будет рекуррентное соотношение и базовый/заключительный кейс?
Рекуррентное соотношение можно выразить следующим уравнением:
Это очевидно, когда смотришь на график треугольника. Еще более примечательно в этой формуле то, что если мы продолжим с ее помощью разбивать любую точку (i, j) на сумму двух других точек, то в итоге неизбежно получим базовый кейс — 1. Треугольник Паскаля начинается с единиц, и из их сумм строится весь сложный паттерн.
Как же нам это реализовать?
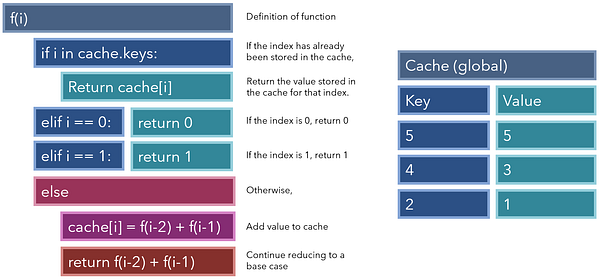
Для начала давайте найдем набор правил, чтобы определять, когда выполняется базовый кейс, при котором значение ячейки равняется 1. Обратите внимание, что 1-цы появляются при выполнении одного из двух условий: когда располагаются либо в первом столбце (j=0), либо по диагонали (i=j).
Теперь выполнить реализацию просто. Если условия для базового кейса выполнены, мы возвращаем базовое значение (1). В противном случае мы продолжаем уменьшать задачу до тех пор, пока не достигнем базового кейса, до которого, как мы определили, будет неизбежно разбит любой ввод.
Теперь рекурсия раскрылась для вас во всей красе. Здесь, с помощью всего пяти строк кода, мы, по сути, создаем саморазвивающееся дерево. При желании число строк кода можно даже уменьшить до трех. Вызывая функцию pascal дважды, мы инициируем две ветви поиска, каждая из которых также инициирует еще две, предполагая, что базовый кейс достигнут не был.
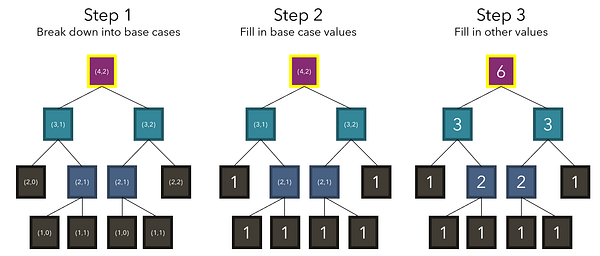
Такая эффективность рекурсии может показаться магической и даже может запутать. Давайте рассмотрим работу ее алгоритма на примере.
В соответствии с нашим рекуррентным соотношением (4, 2) разбивается на (3, 1) и (3, 2), которые являются двумя числами, стоящими над ней. Обратите внимание, что алгоритм на деле не знает, что значения этих ячеек представлены 3. Он просто учитывает их местоположение. Мы не знаем или даже не интересуемся никакими значениями, пока выполняются базовые условия. На основе базовых кейсов (1) мы можем вычислить другие не базовые точки, но для начала должны быть найдены все базовые.
Согласно нашему рекуррентному соотношению, кейсы итеративно разбиваются до тех пор, пока не достигается базовый (j = 0 или i = j). Поскольку нам известны значения этих базовых кейсов (1), мы можем заполнить и другие значения, зависимые от базового кейса.
Это, конечно же, очень, а возможно и чересчур подробное представление принципа работы рекурсивного алгоритма. В действительности ни один из этих трех шагов не нужно программировать, так как они выполняются скриптом автоматически. Все, что вам нужно, — это вызвать функцию внутри ее самой и обеспечить ее завершение в некоторых точках при достижении базового случая.
При вызове return pascal(i-1, j) + pascal(i-1, j-1) мы рассматриваем возврат не как процесс, а как число. Поскольку pascal(i-1, j) инициирует собственные процессы ветвления, а в итоге возвращает другое число (например, 3), будет правильным воспринимать его именно как число, а не как процесс, что может вызвать ненужную сложность и затруднение в понимании.
С некоторой точки зрения этот рекурсивный алгоритм можно назвать неэффективным. В конце концов ‘6′ разбивается на ‘3′, которое, с позиции значения, имеет идентичные разбивки, но при этом зачем-то вычисляется второй раз. Это стандартный случай в рекурсии, когда базовые кейсы одного кейса, будучи вычисленными ранее, вычисляются повторно. Для устранения этой проблемы мы используем мемоизацию.
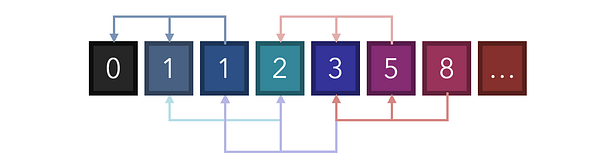
Возьмите в качестве примера последовательность Фибоначчи, в которой первые два числа представлены 0 и 1, а последующие числа являются суммой двух, им предшествующих. На основе уже сформированного знания мы понимаем, что базовыми кейсами здесь будут 0 и 1, а рекуррентное соотношение будет выглядеть как v(i) = v(i-2) + v(i-1). В таком случае мы можем построить простую рекурсивную функцию для нахождения значения последовательности Фибоначчи в любом индексе, начиная с 0.
Обратите внимание, что хоть это и грамотное применение рекурсии, оно весьма неэффективно. 8 разбивается на 3 и 5, а 5, в свою очередь, разбивается на 3 и 2. Мы вычисляем все с самого начала и строим завершенное дерево поиска со множеством повторений.
С помощью мемоизации мы можем решить эту проблему, создав кэш. Это можно реализовать, используя словарь и сохраняя значения, заданные ранее. Например, когда индекс 6 (значение 8) разбивается на индекс 4 и индекс 5 (значения 3 и 5), мы можем сохранить значение индекса 4 в кэше. При вычислении индекса 5 как индекса 3 плюс индекс 4 мы можем извлечь индекс 4 из кэша вместо того, чтобы повторно вычислять его, создавая еще одно обширное дерево, ведущее к базовым кейсам.
Чтобы включить в нашу функцию мемоизацию, мы добавим две функциональности: во-первых, если текущий индекс был сохранен в кэше, мы будем просто возвращать его сохраненное значение; во-вторых, прежде чем продолжать уменьшать значение, мы будем добавлять это значение к кэшу,чтобы ускорить дальнейшие операции. Обратите внимание, что кэш должен быть либо глобальной переменной, либо такой, которую можно извлечь и изменить независимо от области вызова команды.
После добавления мемоизации наша рекурсивная функция стала намного быстрее и мощнее.
Рекурсия занимает центральное место среди многих наибыстрейших алгоритмов сортировки. Цель этих алгоритмов — получить список чисел и вернуть их в порядке от меньшего к большему. Поскольку очень много приложений опираются на быструю сортировку, весьма важно найти такой, который сможет сортировать списки максимально быстро. При этом некоторые из самых быстрых алгоритмов используют рекурсивный подход, называемый “разделяй и властвуй”.
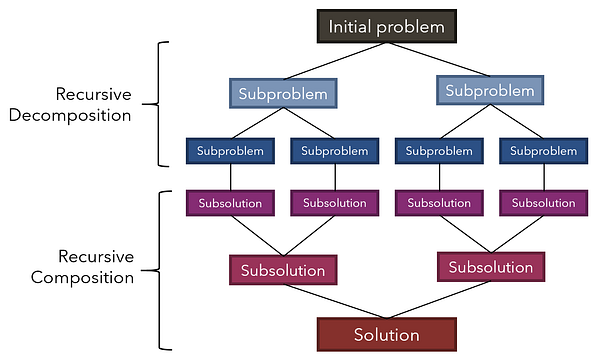
В стратегии “разделяй и властвуй” изначальная задача рекурсивно разбивается на несколько подзадач. После того, как каждая подзадача достигает размера единицы (аналог базового кейса), выявляются их подрешения, которые вновь рекурсивно совмещаются для формирования окончательного решения.
Рассмотрите, к примеру, QuickSort — один из наиболее быстрых алгоритмов сортировки, который при грамотной реализации может выполняться в 2–3 раза быстрее своих соперников и предшественников.
QuickSort начинает выполнение с выбора “опоры”. В простейших реализациях и для наших целей такую опору можно выбрать произвольно. Однако в более специализированных реализациях к ее выбору уже стоит подходить осторожно.
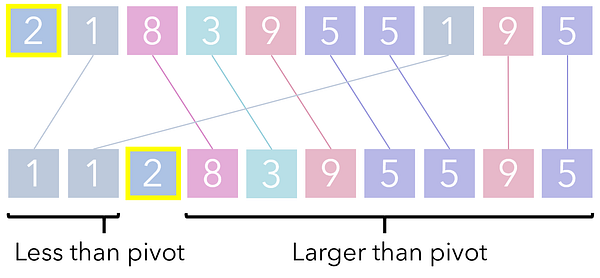
Все элементы со значениями меньше опоры переносятся левее нее, а все, чьи значения больше — правее. Выполнить это можно, пройдя по каждому элементу и переместив те, что меньше опоры, в один список, а те, что больше нее — в другой. Заметьте, что эта операция справляется с задачей только частично.
Процесс сортировки списка на основе его опорной точки называется разделением, так как опора разделяет этот список на два раздела, иначе говоря, на две стороны. Каждый их этих разделов вызывает очередную итерацию разделения сам на себя и так продолжается до тех пор, пока раздел не достигнет базового кейса (1 единицы, просто одного числа)
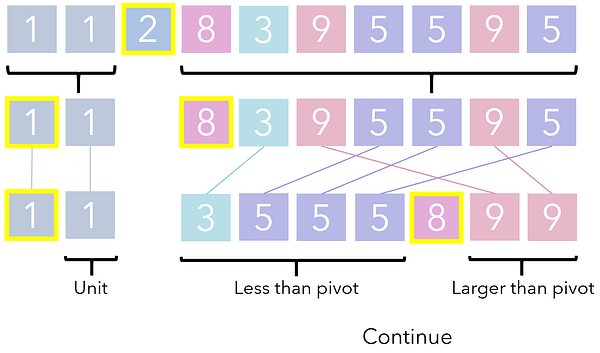
После достаточного числа рекурсивных вызовов исходный список будет разделен до точки, когда эти вызовы продолжить уже невозможно. В этой точке композиция подрешений выполняется простым составлением их в горизонтальном порядке. Результат такой композиции — отсортированный список.
Обратите внимание, что QuickSort следует многим из перечисленных основ рекурсии, рассмотренных нами ранее, только на более высоком уровне. Рекуррентное соотношение является разделением компонента, а базовый кейс — это разделение размера 1. Начиная с оригинального списка, те же процессы (выбор опоры и разделение) вызываются рекурсивно до тех пор, пока результат не будет состоять только из базовых кейсов.
Рекурсия вокруг нас: люди, соборы и капуста романеско
Спойлер: рекурсия есть не только в цифровом мире. Встречается она и в реальном. И намного чаще, чем вы думаете, — разная и интересная.
Валентина Палатурян для Skillbox
Про рекурсивные функции я узнала на уроках информатики. Потом долго считала рекурсию всего лишь отвлечённым понятием из программирования, далёким от реальной жизни. Почему-то в школе нам не рассказывают, что на самом деле явление это встречается в природе, науке, искусстве, а рекурсивные алгоритмы применимы даже для решения бытовых задач.
Что такое рекурсия
В программировании рекурсивная функция — это такая функция, которая вызывает себя из себя же самой, но с другими значениями параметров.
Примечание. Функция может вызывать себя и через промежуточные функции. Например, функция А запускает функцию Б, а та снова вызывает А.
Цепочка вызовов не может быть бесконечной, она должна прерваться и выдать ответ. Поэтому должен возникать крайний случай (или несколько), когда функции уже не нужно вызывать себя с другими параметрами (то есть погружаться ещё глубже), а можно сразу вернуть результат.
Звучит и правда сложно, но не пугайтесь — с примером станет понятнее.
Классический пример рекурсивной функции — вычисление факториала, то есть произведения натуральных чисел от 1 до N.
Здесь N=0 — это крайний случай: функция ничего не вызывает и сразу возвращает единицу (по определению, факториал нуля равен единице).
В более широком смысле рекурсией называют описание или изображение предмета, объекта, явления внутри самого себя. Рекурсивный принцип — это принцип самовоспроизведения и одновременно усложнения системы по одному и тому же алгоритму.
Тут-то и выясняется, что и нас, людей, тоже можно считать рекурсивными: ведь в клетке заложена информация обо всём организме, в ДНК записана информация о том, как синтезировать ДНК.
Фулстек-разработчик. Любимый стек: Java + Angular, но в хорошей компании готова писать хоть на языке Ада.
Рекурсия — не то же самое, что бесконечный цикл
Хотя её часто с ним путают. Понять разницу проще всего на примере. Предположим, ваш начальник издал приказ:
Это не рекурсия. Просто в ситуации, когда начальник не прав, мы попадём в бесконечный цикл вызовов.
Но можно внести небольшое изменение и получить рекурсию:
Приказ стал рекурсивным, потому что в одной из веток вызывает сам себя.
На обед у нас салат «Рекурсивный»: помидоры, огурцы, салат.
Рекурсию можно увидеть
И это очень красиво. Рекурсивные изображения, они же фрактальные паттерны или просто фракталы, — это рисунки или предметы, которые подобны сами себе: состоят из уменьшенных копий себя.
Подобным же образом выстроены кровеносные сосуды и нервы в организме животных. Свойствами фракталов обладают снежинки, а ещё — удивительная капуста романеско. Вот она на картинке ниже — ну разве не красавица? 😀
В архитектуре рекурсия встречается в облике готических соборов.
В этом соборе XIII века задействован один из характерных для готики приёмов: его окна украшены тонкими ажурными перегородками. Их основной узор — стрельчатая арка с кругом внутри, круг поддерживается двумя арками меньшего размера.
А вот рекурсивная версия того же узора — Собор Линкольна.
Здесь окно тоже выполнено в форме остроконечной арки с вписанным в неё кругом, а круг лежит на двух других арках. Вот только внутри каждой из этих арок — снова круг и две ещё меньших арки, а внутри них — ещё по одному кругу на двух меньших арках.
Другой пример архитектурной рекурсии — собор Святого Петра в Ватикане.
Джордж Херси, американский писатель и журналист, сравнивал его с китайскими шкатулками с секретом. По его словам, архитектурный комплекс состоит из одной макроцеркви, четырёх наборов того, что журналист назвал макси-церквями, 16 мини-церквей и 32 микроцерквей. А мог бы просто сказать, что собор рекурсивный.
В изобразительном искусстве рекурсия тоже отметилась — взять хотя бы «Триптих Стефанески» Джотто. На его центральной панели изображён кардинал Стефанески, которой держит в руках этот же триптих (на котором тоже изображён триптих и так далее).
А вот пример посвежее — литография «Рисующие руки» нидерландского художника XX века Маурица Эшера:
Чтобы увидеть рекурсию, необязательно идти в картинную галерею — просто посмотрите на герб России. Двуглавый орёл держит в правой лапе скипетр, который увенчан двуглавым орлом, а тот тоже держит скипетр, который… 🙂 В общем — вот:
Рекурсию можно услышать
В музыке есть композиции, которые тоже можно назвать рекурсивными. Американский физик и писатель Дуглас Хофштадтер в своей книге «Гёдель, Эшер, Бах: эта бесконечная гирлянда» рассказывает о рекурсии, приводя в пример джигу из «Французской сюиты №5» Баха.
В первой её части трижды повторяется мелодический переход из тональности соль мажор в ре минор: мелодия как бы вызывает сама себя, погружаясь всё глубже. А во второй части, наоборот, трижды поднимается от ре к соль.
Программисту это может напомнить вычисление факториала числа 3: функция трижды вызывает саму себя, затем трижды возвращается с промежуточными результатами вычислений, а затем — с итоговым.
В лингвистике рекурсией называют способность языка порождать вложенные предложения и конструкции. Например, предложение «Саша читает статью про рекурсию» можно достроить до «Лена смотрит, как Саша читает статью про рекурсию». А его, в свою очередь, превратить в «Ленин друг Петя не одобряет, что Лена смотрит, как Саша читает статью про рекурсию».
Принято считать, что рекурсия свойственна любому человеческому языку (сомнения пока есть только насчёт языка пираха, на котором разговаривают в бразильской части бассейна Амазонки), а распознавать и понимать её — едва ли не врождённая способность людей.
Чтобы доказать это, немецкие учёные даже ставили эксперименты на пятимесячных младенцах. Они измеряли активность головного мозга с помощью ЭЭГ — и сравнивали реакцию малышей на вложенные языковые конструкции, правильные и неправильные. Так как дети были настолько малы, что речь ещё не понимали, вместо слов им проигрывали последовательности звуков разной частоты. Причём частоты звука для связанных слов во вложенных конструкциях совпадали.
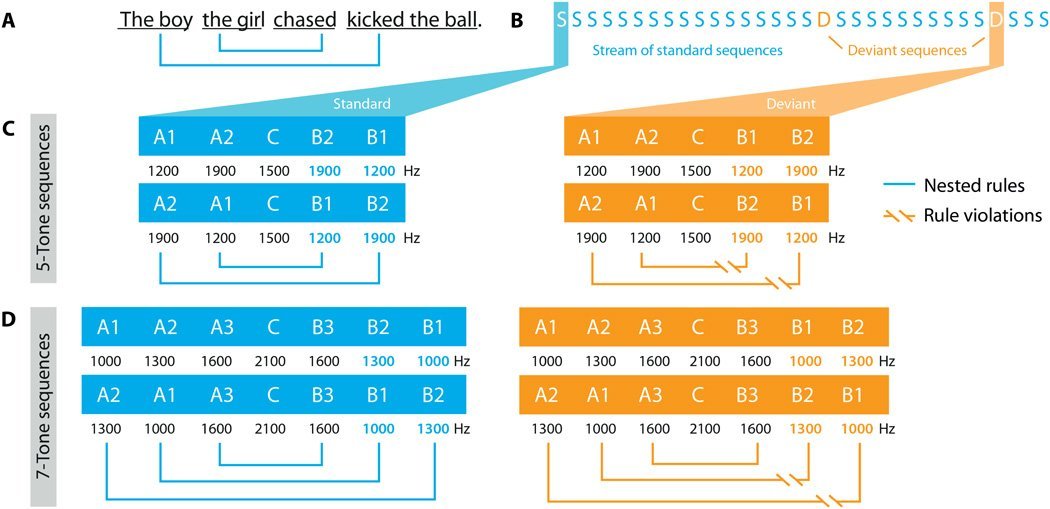
В предложении «Мальчик, за которым гналась девочка, пнул мяч» две связанные конструкции: 1) «мальчик пнул» и 2) «девочка гналась». Их обозначили звуками частотой 1900 и 1200 Герц и разделили коротким звуком в 1500 Герц. Слева — корректные, а справа — некорректные языковые паттерны. Кроме пятитоновых, проигрывались и семитоновые вложенные последовательности.
Научные подробности ищите в оригинальной публикации. Нам важнее выводы: эксперименты показали, что даже мозгу младенцев неправильные конструкции определённо не понравились.
Конечно, выборка (38 участников) слишком мала, чтобы распространять результаты на всё человечество, но теория интересная.
Рекурсивные алгоритмы легко смоделировать с помощью подручных средств
Возьмите, например, матрёшку. Все вложенные в неё куклы подобны кукле-шкатулке, кроме наименьшей, которая представляет собой базовый случай. То есть матрёшка — твёрдое воплощение рекурсии.
А если задаться целью поставить синюю точку на самой маленькой кукле, то можно буквально на пальцах реализовать рекурсивный алгоритм:
А вот алгоритм, для исполнения которого не нужны дополнительные предметы. Представьте, что вы сидите в последнем ряду длинного зала и хотите узнать, сколько всего в нём рядов. Конечно, можно встать и пересчитать их, но вам лень, а ещё вы уже знаете про рекурсию.
Так что вы спрашиваете соседа спереди, сколько перед ним рядов. Если он называет какое-то число, вы прибавляете к нему ещё два (один ряд — для соседа и один — тот, в котором сами сидите) и получаете ответ, а иначе — предлагаете этому самому соседу применить ваш гениальный алгоритм уже к его соседу спереди.
Если все участники процесса будут настроены доброжелательно, то в итоге очередь отвечать дойдёт до первого ряда и вам обратно по цепочке вернут результат — полученный с помощью рекурсивного алгоритма, между прочим. То есть:
И минутка предметного юмора
— Помнишь, Антоха желание проиграл? Так вот, я ему загадал, чтобы он два дня на все предметы, с которыми что-то сделал, клеил стикер с названием этого действия.
— И что, он на каждый новый стикер клеил другой с надписью «наклеил»?
Подытожим
Рекурсивные предметы и явления окружают нас повсюду. Рекурсию можно увидеть, услышать, потрогать руками. Рекурсия — это просто. Чтобы понять её, не обязательно разбираться с фракталами или фугами Баха. Объяснить рекурсию можно даже пятилетнему ребёнку. Просто прочтите ему стишок Андрея Усачёва:
Шёл по улице жучок
На груди блестел значок,
Нарисован был жучок,
И на нём висел значок,
Был ещё один жучок…
Что глядел я целый час
Был ли у жучка значок?
Был ли на значке жучок?
Тональность — музыкальный термин. Определяется тоникой (опорная, главная нота музыкального произведения) и типом лада (мажор или минор).
ЭЭГ — электроэнцефалограмма, регистрирует электрические сигналы клеток головного мозга.