для чего нужны жесткие вставки в лире
11. Использование жестких вставок при моделировании конструкций в ПК ЛИРА 10.4
Помимо рассмотренной в предыдущей заметке проблемы учета тела колонны при расчете перекрытий, расчетчики часто сталкиваются с вопросами моделирования ребристых перекрытий и капителей.
Жесткие вставки используются, как правило, при нарушении соосности стыковки стержней в узле. Например, при моделировании двухступенчатой колоны (стык подкрановой и надкрановой части колонны), примыкание ригеля к колонне, моделирование ребристых плит и т.п. Рассмотрим на примерах, какие различия получаются при расчетах с учетом жестких вставок и без них.
1. Моделирование ребристого перекрытия
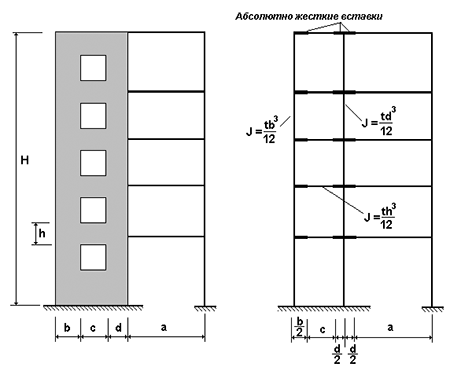
Рис. 1. Расчетные модели зданий. ПК ЛИРА 10.4
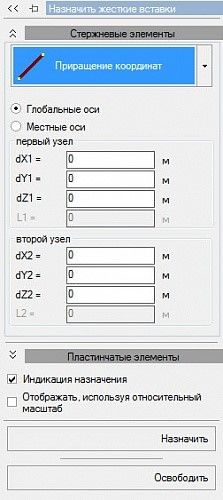
Рис. 2. Панель настроек жестких вставок. ПК ЛИРА 10.4
Жесткие вставки ориентируются вдоль осей, глобальной и местной системы координат, по линейным направлениям X, Y, Z. При этом нагрузки, задаваемые на стержень с жесткими вставками, привязываются к началу гибкой части. Заданный шарнир располагается между жесткой вставкой и гибкой частью стержня. Усилия вычисляются только в гибкой части стержня, поэтому при проверке равновесия в узле, где присутствует такой стержень, следует производить перенос усилий из гибкой части стержня в узел, с учётом заданной нагрузки на жесткую вставку. Проанализируем результаты расчетов по подобранной арматуре в прекрытиях 1-го этажа зданий (рис. 3), слева армирование без жестких вставок, справа с их применением.
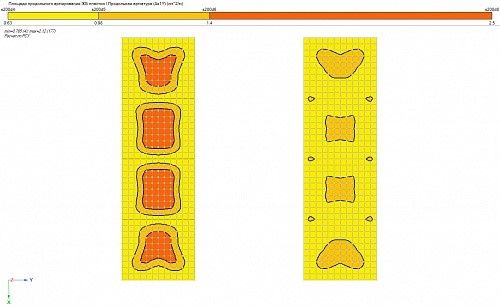
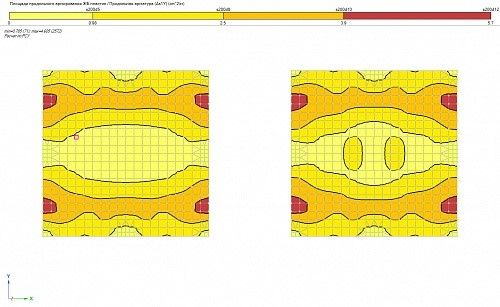
Рис. 3. Продольное армирование As1y плит перекрытия 1-го этажа. ПК ЛИРА 10.4
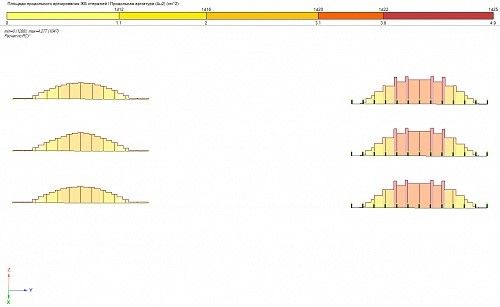
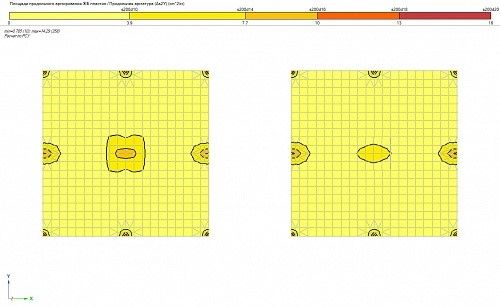
Рис. 4. Угловое армирование Au2 балок перекрытия 1-го этажа. ПК ЛИРА 10.4
Как видно, различные способы моделирования дают различные результаты как по значениям, так и по характеру армирования.
2. Моделирование капителей
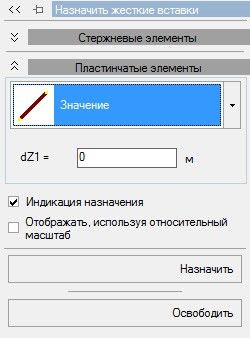
Помимо жестких вставок для стержней в ПК ЛИРА 10.4 реализованы жесткие вставки и для пластинчатых элементов (рис. 5).
Рис. 5. Панель задания жестких вставок для пластинчатых КЭ. ПК ЛИРА 10.4
Данный вид жестких вставок позволяет успешно моделировать такие часто встречающиеся элементы строительных конструкций, как капители (рис. 6).
Рис. 6. Модель для сравнения расчета с учетом капителей и без. ПК ЛИРА 10.4
Результаты расчетов по 2-м различным схемам приведены на рисунках 7 и 8.
Рис. 7. Нижнее армирование As1y. ПК ЛИРА 10.4
Рис. 8. Верхнее армирование As2y. ПК ЛИРА 10.4
Как видно из рисунков, задание жестких вставок приводит к более верному распределению арматуры, т.е. нижнее армирование больше, чем в случае без капителей, а верхнее, напротив – меньше.
Заметки инженера-строителя
Блог проектировщика
Полезная информация о конструкциях, расчётах и строительных материалах
Содержание сайта: Главная страница
воскресенье, 30 сентября 2018 г.
Абсолютно жёсткие вставки. Абсолютно жесткие тела. Что такое, в чём разница, куда назначают
Абсолютно жесткие вставки используются, как правило, при нарушении соосности стыковки стержней в узле.
В месте примыкания колонн, пилонов и стен к перекрытиям и покрытиям формируется АЖТ.
АЖТ призвано уменьшить значение изгибающих моментов, возникающих на опоре и избежать пика армирования плиты внутри сечения колонны, пилона или стены.
То есть внутри сечения колонны, пилона или стены получается как бы бесконечная жесткость, а армирование плиты нужно начинать только с грани колонны, пилона или стены.
Моделирование конструкций с использованием абсолютно жестких вставок:
Про использование абсолютно жёстких вставок в SCAD можно прочитать здесь: ссылка
Про использование абсолютно жёстких вставок в ПК Лира Софт можно прочитать здесь: ссылка
При введении в стержневые элементы абсолютно жестких вставок гибкая часть стержня отодвигается от узлов элемента на длину задаваемой абсолютно жесткой вставки. При этом нагрузки, задаваемые на стержень с абсолютно жесткими вставками, привязываются к началу гибкой части. Усилия вычисляются только в гибкой части стержня, и, поэтому, при проверке равновесия в узле, где присутствует такой стержень, нужно производить перенос усилий из гибкой части стержня в узел, с учётом заданной нагрузки на жесткую вставку.
Абсолютно жесткие вставки используются, как правило, при нарушении соосности стыковки стержней в узлах для учета эксцентричности стыковки элементов:
— при моделировании двухступенчатой колонны (стык подкрановой и надкрановой частей колонны):

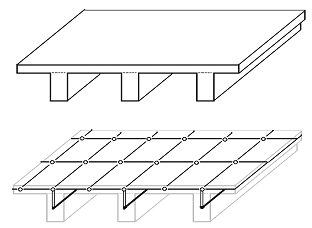
— при моделировании рёбер в плитах и оболочках, подпёртых (подкреплённых) рёбрами, эксцентрично расположенными по отношению к срединной поверхности
(продольные оси ребер, моделируемых стержнями, не лежат в срединной плоскости плиты)
Для этого на концах стержней, моделирующих ребра плиты, вводят жесткие вставки, через которые стержень прикрепляют к узлам плиты:
Влияние на напряженно-деформированное состояние: При моделировании с использованием абсолютно жестких вставок общий изгиб оребренной плиты представляется в виде изгиба плитной части конструкции и пары сил, образованной мембранными напряжениями плиты (оболочечного элемента) и продольной силой в стержне:
Подробнее см. Скорук Л. «Поиск эффективных расчётных моделей ребристых железобетонных плит и перекрытий»
Здесь стоит отметить, что для плит с широкими ребрами моделировать следует не с использованием абсолютно жестких вставок, а с использованием абсолютно жестких тел, так как изгиб плиты в пролете между подкрепляющими ребрами будет заметно большим, чем в том случае, когда будет учитываться сокращение пролета плиты за счет ширины ребра.
— при моделировании смещения расчётной оси, проходящей через центр тяжести в местах изменения толщины поясов рам переменного сечения:
— при моделировании этажного опирания балок
— при моделировании примыкания к колонне ригелей разной высоты
Более подробно с нюансами применения абсолютно жестких вставок и жестких тел можно ознакомиться в труде А.С. Городецкого, И.Д. Евзерова «Компьютерные модели конструкций», Киев, «Факт», 2005
*Статья создана не без использования указанных выше источников.
Использование бесконечно жестких вставок
Широко известно, что плохо обусловленные матрицы жесткости часто появляются в тех случаях, когда в одном узле конечно-элементной модели сопрягаются элементы с резко отличными жесткостными параметрами. Покажем на простом примере, как можно интерпретировать такую ситуацию в терминах механики. Оказывается, что плохая обусловленность присуща « почти изменяемым » конструкциям.
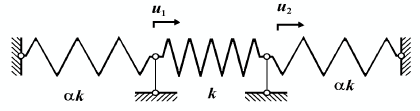
На рис. 1 представлена формально неизменяемая система, матрица жесткости которой имеет вид
Собственные числа этой матрицы λ1 = α; λ2 = 2 + α, а число обусловленности
При большой жесткости средней пружины по сравнению с жесткостью крайних пружин параметр α мал, и число H становится большим, что говорит о плохой обусловленности и возможной потере точности при решении уравнений с такой матрицей.
Рис. 1. Схема с плохо обусловленной матрицей жесткости
Нетрудно заметить, что механическое поведение рассматриваемой конструкции приближается к поведению изменяемой системы. Действительно, возможно перемещение средней пружинки как жесткого тела при пренебрежимо малом сопротивлении крайних пружинок. Их реакция ввиду приведенного соотношения жесткостей вызывает ничтожную деформацию средней компоненты системы. Если же изменить соотношение жесткостей на обратное, то матрица жесткости будет иметь число обусловленности H ≈ 1. В узле снова сходятся элементы с резко отличными жесткостями, но матрица жесткости хорошо обусловлена и соответствует теперь упругой конструкции (средней пружинке), присоединенной к земле практически недеформируемыми связями. Стоит заметить, что отыскание «почти изменяемости», основанной на сопоставлении порядков возможных деформаций, может свидетельствовать как о некотором пороке конструкции, так и о порочности ее моделирования.
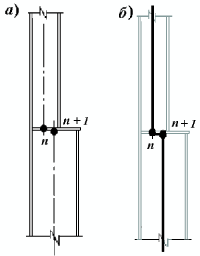
Рис. 2. Ступенчатый стык
Не останавливаясь на анализе первого случая, когда, по-видимому, конструктор должен изменить систему, заметим, что для второго случая часто удается найти достаточно простой выход из положения, когда элемент с резко завышенной жесткостью объявляется абсолютно жестким, и это свойство учитывается на уровне составления системы разрешающих уравнений путем введения соответствующих связей.
Так, например, при расчете стержневых систем часто возникает необходимость учесть эксцентричность стыковки элементов в узлах (рис. 2, а ).
Вставка между узлами n и n+1 стержня с очень большой, но конечной жесткостью, как это представляется интуитивно возможным, приводит, как это было показано выше, к резкой потере точности вычислений за счет ухудшения обусловленности матрицы жесткости.
Для обхода этой вычислительной трудности предусматривается возможность использовать бесконечно жесткие вставки по концам стержневых элементов. Тогда расчетная схема имеет только один узел, занимающий произвольное положение на прямой между узлом n и узлом n +1, и концевые сечения соседних элементов присоединяются к этому узлу через жесткие вставки. Потеря точности в этом случае не наблюдается.
Проще всего можно поступить, если этот единственный узел N совместить с узлом n или n +1, тогда абсолютно жесткая вставка появится только у одного из элементов. Платой за это упрощение является то, что внутренние усилия будут определены лишь на упругой части стержня.
Рис. 3. Ребристая плита
Использование абсолютно жестких вставок широко практикуется в тех случаях, когда рассматривается плита или оболочка, подкрепленная ребрами, эксцентрично расположенными по отношению к срединной поверхности. Если эти ребра моделируются стержневыми элементами, то учесть эксцентриситет легко и удобно, используя абсолютно жесткие вставки (рис. 4). При этом расчетные узлы располагаются на уровне срединной поверхности плиты. Можно, однако, расположить узлы на уровне центров тяжести ребер и воспользоваться опцией «смещение срединной плоскости пластин», что приведет к такому же эффекту. Такой прием удобен, например, в тех случаях, когда проектируется балочная клетка, часть которой перекрывается настилом. Необходимо отметить, что эксцентричность расположения ребер сказывается на результатах, относящихся к мембранной группе усилий, поэтому учет эксцентриситета в конструкции чисто изгибаемого типа (и набранной из соответствующих конечных элементов) ничего не дает.
Рис. 4. Использование абсолютно жестких вставок для учета размеров узлов
При расчете стержневых систем высота сечения обычно не превышает 1/8÷1/10 расстояния между узлами. Но встречаются конструкции, когда это отношение доходит до 1/5 или даже 1/3 (некоторые виды фундаментов под турбоагрегаты, диафрагмы зданий, гидротехнические сооружения и др.). В этом случае стержневая расчетная схема с точечными узлами, расположенными на пересечениях осей элементов, становится некорректной. Широко распространено предложение учитывать при этом реальные размеры «узлов», используя для этих целей стержневые элементы с бесконечно жесткими вставками. Пример такой схемы, построенной в соответствии с рекомендациями [3], дан на рис. 4.
Этот прием настолько давно используется, что расчетчики практически никогда не задают вопрос о правомерности использования гипотезы недеформируемости «узла». Вместе с тем он далеко не лишен смысла, что видно из рассмотрения результатов расчета модельной задачи (рис. 5).
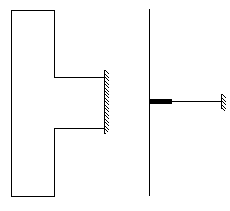
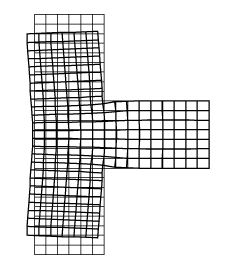
Рис. 5. К анализу работы узла конечных размеров
В ее стержневой модели горизонтальные перемещения отсутствуют, и вертикальный стержень не изгибается. Более детальная расчетная схема указывает на наличие горизонтальных перемещений, которые возникают вследствие стеснения деформаций сжатия по линии сопряжения АБ. Поскольку на противоположной стороне «стойки» этого стеснения нет, то возникает неравномерность распределения напряжений, эквивалентная изгибу.
Жесткие вставки или элементы большОй жесткости?
Доброго времени суток.
Уважаемые форумчане, подскажите.
Необходимо посчитать каркас железобетонного здания сложной формы (см. вложение)
Железобетон сборный, колонны ступенчатые. в среднем пролете балки в нескольких уровнях опираются на колонны с разным сечением (ступенчатые колонны)
в любом случае буду делать две расчетные схемы, просто на первых порах хотелось бы получить информацию для размышлений и узнать путь следования
я что-то в схему не въехал. О каких ригелях речь, может, нарисуете? Что понимается под колонной, тогда будет ясно, что слева, а что права. Жестких вставок у стержня 3 по разным осям.
Минус жестких вставок ещё в том, что придётся задавать их в двух направлениях. Если поперек оси стержня длина вставки известна, то вдоль стержня придётся вычислять.
Можно использовать абсолютно жесткие тела.
пытаюсь быть инженером
пытаюсь быть инженером
параллельно еще вопрос возник. как замоделировать двухветвенную колонну ЖБ? как двутавровую, только с очень тонкой стенкой?)
пытаюсь быть инженером
на сколько я помню и знаю, такая колонна считается в расчетной схеме как один стержень, потом моменты и продольные силы раскладываются на каждую из ветвей. и далее считается ветвь отдельно по заданным усилиям и в зависимости от длины, на которую ветвь разбивается раскосами(решеткой). но это расчет «ручками».
вопрос в том, как задать это в лире? и если задать эту колонну как двутавровое бетонное сечение с тонкой стенкой, Лира правильно заармирует его (или есть другие способы вносить такие сечения в расчетную схему)?
вопрос возник «параллельно», потому что нужно определить усилия в элементах, а затем проверить существующие сечения колонн и подобрать армирование.
Offtop: и еще. может особо знающие и сведующие люди будут смеяться, но этот каркас нужно посчитать на сейсмику. не простой статический расчет.
Как задать жесткие вставки в Лире?
Строительство и все с ним связанное
Попытаюсь ответить:
Алгоритм задания АЖВ
— чертишь свою конструкцию
— выбираешь стержень,который моделирует твое ребро в плите
— жмакай на кнопочку жесткие вставки появляется панель
— задаешь,насколько необходимо отступить узлам данного стержня от прежнего положения ( в твоем случае 300)
— обрати особое внимание на положение местных осей стержня
у меня все получилось!
PS Еще советую прочесть про это в хорошей книжичке «Расчет и пректирование конструкций высотных зданий из ЖБ» раздел 4 «Плиты перекрытия усиленные балками»
[ATTACH]1134041859.JPG[/ATTACH]
дискретизатор континуума (бывший)
Разработчики программ (в частности Лиры) рекомендуют ребристые перекрытия проектировать следующим образом: задается плита и к ней «подвешивается» балка на жестких вставках. Высота балки задается за вычетом толщины плиты.
Решение вроде-бы логичное- система моделирует реальную работу перекрытие, кроме того, нет учета двойной жесткости как это бывает при задании балки в теле плиты.
Прилагаю задачу с жесткими вставками в Лире (СКАДа, к сожалению, не имею).
Теперь вопросы.
1.Эпюра изгиб моментов выглядит нереально как для рамной конструкции.
2. Как армировать такие балки?
Знаю, что некоторые продвинутые конструкторы используют такую систему.
Как Вы справляетесь с этой задачей? [sm2102]
[ATTACH]1150701922.zip[/ATTACH]
Проектирование (капитальный ремонт, реконструкция, модернизация)