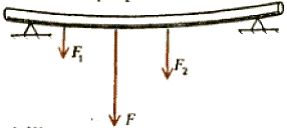
для чего у динамометров делают ограничители растяжения пружин
Динамометр
Содержание
В данном уроке мы познакомимся с новым прибором, который называется динамометром. С его помощью можно измерить силу, действующую на тело.
Динамометр – это прибор для измерения силы.
Слово “динамометр” образовано от двух греческих слов: “динамис” – сила и “метрео” – измеряю.
Рассмотрим самый простой вид динамометра – пружинный. Это поможет нам разобраться с принципом действия прибора. Основной его частью является стальная пружина.
Не сложно догадаться, что если подвесить к пружине груз, то она растянется. Другими словами, наблюдатель видит, что на подвешенное тело действует сила, и может определить ее величину.
Пружинный динамометр
Простой пружинный динамометр можно изготовить самостоятельно (рисунок 1). Он состоит из нескольких частей:
Сначала закрепляем пружину на корпусе таким образом, чтобы ее нижний конец оставался свободным. Затем к нему прикрепляем указатель. Если разогнуть последний виток пружины, то его можно использовать в качестве указателя.
Шкалу можно изготовить из полоски обычной бумаги, нанеся на нее штрихи и числа. Поэтому приклеим бумагу на корпус и сделаем на ней первую отметку (рисунок 2, а). Это будет нулевая отметка, которая показывает, где заканчивается нерастянутая пружина.

Если пружина прекратила растяжение и груз остановился, это означает, что сила тяжести, действующая на тело, и сила упругости пружины уравнялись. Новое положение указателя отметим на бумаге, поставив цифру 1 (рисунок 1, б).
Так мы уже получили начало шкалы и необходимо ее продолжить. И сделать это можно по-разному:
Теперь у нас есть шкала, которая позволяет измерять силу с точностью до целых. Но точность нашей шкалы можно улучшить до десятых, нанеся на нее дополнительные деления – 0,1; 0,2; 0,3; 0,4 и т. д.
Для этого разделим расстояние между отметками 0 и 1 на 10 одинаковых частей, поставив соответствующие штрихи. Аналогично поделим на части и другие отрезки ( между отметками 2 и 3, 3 и 4, и т. д.).
Принцип действия динамометра
Итак, мы видим, что для измерения силы, действующей на груз, необходимо уравнять ее с силой растяжения пружины динамометра. Указатель, закрепленный на пружине, покажет величину этой силы согласно шкале. Таким образом, можно сделать вывод, что:
Устройство динамометра основывается на сравнении измеряемой силы с силой упругости пружины.
Например, если подвесить груз какой-то массы, то мы будем сравнивать силу тяжести, действующую на этот груз, и величину силы упругости растянутой пружины.
Если мы возьмем крючок на конце пружины и потянем за него, то мы будем сравнивать силу, приложенную нами, с силой упругости пружины. Так, с помощью динамометра можно измерять различные силы.
Вспомним закон Гука – он гласит, что сила упругости тела при растяжении прямо пропорциональна изменению длины тела. Принцип работы динамометра подтверждает этот закон – пружина удлиняется во столько же раз, во сколько увеличивается сила ее упругости.
Виды динамометров
Можно выделить несколько видов динамометров на основе принципа их действия:
В основе работы механических динамометров лежит деформация. Принцип действия пружинного динамометра подробно описан выше. В рычажном динамометре под действием измеряемой силы происходит деформация рычага, которая и показывает величину силы.
Принцип действия таких динамометров основан на определении количества жидкости, вытесняемой из цилиндра под действием измеряемой силы.
У таких динамометров имеется датчик, который преобразует деформацию в электрический сигнал. Это вид динамометров стал широко применяться в последнее время.
Современные модели динамометров могу соединять и использовать в себе несколько принципов действия.
Применение динамометров
Динамометры имеют очень широкое применение. Например, в медицине используются специальные медицинские динамометры. Они предназначены для измерения силы различных мышечных групп человека.
Одним из таких приборов является ручной динамометр, который называется силомером (рисунок 3). С его помощью измеряется мускульная сила руки при сжатии кисти в кулак.
Рисунок 3. Силомер – электронный кистевой динамометр.
Для того чтобы измерить тяговые усилия локомотивов, тракторов, морских буксиров и другой техники, используют специальные тяговые динамометры (рисунок 4).

Такие динамометры способны измерять силы до нескольких десятков тысяч ньютонов. Современные модели имеют пульт дистанционного управления с дисплеем (рисунок 5).
Рисунок 5. Тяговый динамометр.
При монтаже проводов и кабелей используют динамометры для определения силы натяжения провода (рисунок 6). Существуют специальные монтажные таблицы с необходимыми значениями.
Рисунок 6. Динамометр для монтажных работ.
Динамометры используют не только в специальной технике, но и в обычных для нас местах: в метро, в автобусах и даже в лифте. Здесь эти приборы используют для измерения силы сжатия створок различных автоматических дверей.
Учебники
Журнал «Квант»
Общие
А так ли хорошо знакомы вам деформации? // Квант. — 1994. — № 3. — С. 32-33.
По специальной договоренности с редколлегией и редакцией журнала «Квант»
. сила любой пружины пропорциональна ее растяжению.
Содержание
Конечно же, в утверждении Гука речь идет об одной из самых наглядных — об упругой деформации. Однако в школе дается представление и о других видах деформаций, изучение которых играет огромную роль. Вспомните задачи об упругих и неупругих ударах, о равновесии тел, об изменении формы и объема тел, о механических колебаниях… Список настолько велик, а понимание связанных с деформациями механических свойств тел столь важно для науки и техники, что можно без преувеличения говорить об исследовании этих свойств как об одной из главных задач современной физики.
Получается, что и в школьном курсе к понятию деформации приходится обращаться не раз и в различных его частях. На макроскопическом уровне — в механике и при изучении тепловых явлений; при объяснении взаимодействия атомов и молекул — в кинетической теории вещества; при выявлении природы упругих сил — в электромагнетизме. Поэтому так разнообразны ситуации, в которых вы сегодня встретитесь с этим отнюдь не второстепенным понятием.
Вопросы и задачи
Микроопыт
Поставьте вертикально резиновую трубку, на которую предварительно туго надето металлическое кольцо, и растяните трубку. Что при этом произойдет с кольцом? Почему?
Любопытно, что.
. научные интересы Гука были столь широки, что он часто не успевал доводить свои исследования до конца. Это давало повод к острейшим спорам о приоритете в открытии тех или иных законов с крупнейшими учеными (Гюйгенсом, Ньютоном и др.). Однако «закон Гука» был настолько убедительно обоснован многочисленными экспериментами, что тут приоритет Гука никогда не оспаривался.
. в начале XVIII века участились аварии на рудниках, связанные с разрывом железных цепей, применяемых в шахтных подъемниках. Попытки модернизировать цепи предпринимали многое ученые, в том числе и знаменитый математик и философ Г.Лейбниц. Но — безуспешно. А вот старшему горному советнику, юристу по образованию, В. Альберту пришла в голову идея заменить цепи проволочными канатами или тросами. Это позволило использовать такое важное свойство железа, как прочность на растяжение.
. побеление мокрого песка при ходьбе по нему впервые удалось объяснить в 1885 году английскому физику и инженеру О.Рейнольдсу. Он показал, что под действием возникающей под ногой деформации сдвига объем, занимаемый песчинками, увеличивается и песок некоторое время находится выше уровня воды.
. одиночные кристаллы многих металлов, выросшие из расплава, оказываются настолько мягкими, что их легко согнуть пальцами. А вот разогнуть — уже не удается. Это — пример замечательной способности пластически деформируемых тел упрочняться.
. объяснение пластической деформации возникло лишь тогда, когда физики (уже в нашем столетии) открыли так называемые дислокации — дефекты кристаллической решетки твердого тела. С современной точки зрения, этот вид деформации есть «движение беспорядка» вдоль кристалла.
. на сегодняшний день получены особые сверхупругие сплавы, напоминающие поведением резину и способные выдерживать огромные упругие деформации — на два порядка больше, чем обычные металлы. С другой стороны, многие сплавы можно привести в сверхпластичное состояние, когда они при очень низких напряжениях текут, подобно разогретому стеклу.
. совместить противоположные механические характеристики удается в композитах — «сборных» материалах, включающих легкую и пластичную основу и наполнители из тонких волокон очень прочного вещества.
. можно измерить деформации, меньшие диаметра атома, правда, если они носят колебательный характер — тогда их легко преобразовать в электрические сигналы. Кстати, ухо человека способно «измерить» столь же малые деформации барабанной перепонки.
. при деформации кварца и некоторых других диэлектриков на их поверхности возникают электрические заряды, а поляризация диэлектриков в электрическом поле может привести к их деформации. Эти явления называют прямым и обратным пьезоэлектрическим эффектом.
. если достаточно долго облучать свинец нейтронами, в нем происходит внутренняя перестройка и он становится настолько упругим, что изготовленный из него колокол мог бы звучать не хуже отлитых из лучшей колокольной бронзы.
Что читать в «Кванте» о деформациях
(публикации последних лет)
Ответы
Микроопыт
Поскольку при растяжении трубки уменьшается диаметр ее поперечного сечения, кольцо упадет вниз.
Для чего у динамометров делают ограничители растяжения пружин
Kvant. Деформации — PhysBook
А так ли хорошо знакомы вам деформации? // Квант. — 1994. — № 3. — С. 32-33.
По специальной договоренности с редколлегией и редакцией журнала «Квант»
… сила любой пружины пропорциональна ее растяжению.
Конечно же, в утверждении Гука речь идет об одной из самых наглядных — об упругой деформации. Однако в школе дается представление и о других видах деформаций, изучение которых играет огромную роль. Вспомните задачи об упругих и неупругих ударах, о равновесии тел, об изменении формы и объема тел, о механических колебаниях… Список настолько велик, а понимание связанных с деформациями механических свойств тел столь важно для науки и техники, что можно без преувеличения говорить об исследовании этих свойств как об одной из главных задач современной физики.
Получается, что и в школьном курсе к понятию деформации приходится обращаться не раз и в различных его частях. На макроскопическом уровне — в механике и при изучении тепловых явлений; при объяснении взаимодействия атомов и молекул — в кинетической теории вещества; при выявлении природы упругих сил — в электромагнетизме. Поэтому так разнообразны ситуации, в которых вы сегодня встретитесь с этим отнюдь не второстепенным понятием.
Вопросы и задачи
Микроопыт
Поставьте вертикально резиновую трубку, на которую предварительно туго надето металлическое кольцо, и растяните трубку. Что при этом произойдет с кольцом? Почему?
Любопытно, что…
… научные интересы Гука были столь широки, что он часто не успевал доводить свои исследования до конца. Это давало повод к острейшим спорам о приоритете в открытии тех или иных законов с крупнейшими учеными (Гюйгенсом, Ньютоном и др.). Однако «закон Гука» был настолько убедительно обоснован многочисленными экспериментами, что тут приоритет Гука никогда не оспаривался.
… в начале XVIII века участились аварии на рудниках, связанные с разрывом железных цепей, применяемых в шахтных подъемниках. Попытки модернизировать цепи предпринимали многое ученые, в том числе и знаменитый математик и философ Г.Лейбниц. Но — безуспешно. А вот старшему горному советнику, юристу по образованию, В. Альберту пришла в голову идея заменить цепи проволочными канатами или тросами. Это позволило использовать такое важное свойство железа, как прочность на растяжение.
… побеление мокрого песка при ходьбе по нему впервые удалось объяснить в 1885 году английскому физику и инженеру О.Рейнольдсу. Он показал, что под действием возникающей под ногой деформации сдвига объем, занимаемый песчинками, увеличивается и песок некоторое время находится выше уровня воды.
… одиночные кристаллы многих металлов, выросшие из расплава, оказываются настолько мягкими, что их легко согнуть пальцами. А вот разогнуть — уже не удается. Это — пример замечательной способности пластически деформируемых тел упрочняться.
… объяснение пластической деформации возникло лишь тогда, когда физики (уже в нашем столетии) открыли так называемые дислокации — дефекты кристаллической решетки твердого тела. С современной точки зрения, этот вид деформации есть «движение беспорядка» вдоль кристалла.
… на сегодняшний день получены особые сверхупругие сплавы, напоминающие поведением резину и способные выдерживать огромные упругие деформации — на два порядка больше, чем обычные металлы. С другой стороны, многие сплавы можно привести в сверхпластичное состояние, когда они при очень низких напряжениях текут, подобно разогретому стеклу.
… совместить противоположные механические характеристики удается в композитах — «сборных» материалах, включающих легкую и пластичную основу и наполнители из тонких волокон очень прочного вещества.
… можно измерить деформации, меньшие диаметра атома, правда, если они носят колебательный характер — тогда их легко преобразовать в электрические сигналы. Кстати, ухо человека способно «измерить» столь же малые деформации барабанной перепонки.
… при деформации кварца и некоторых других диэлектриков на их поверхности возникают электрические заряды, а поляризация диэлектриков в электрическом поле может привести к их деформации. Эти явления называют прямым и обратным пьезоэлектрическим эффектом.
… если достаточно долго облучать свинец нейтронами, в нем происходит внутренняя перестройка и он становится настолько упругим, что изготовленный из него колокол мог бы звучать не хуже отлитых из лучшей колокольной бронзы.
Что читать в «Кванте» о деформациях
(публикации последних лет)
Ответы
Микроопыт
Поскольку при растяжении трубки уменьшается диаметр ее поперечного сечения, кольцо упадет вниз.
Динамометр. Виды и устройство. Работа и применение. Как выбрать
Динамометр представляет собой специальное устройство, предназначенное для измерения показателей силы или получения параметров момента действующей силы. Этот измерительный прибор способен определить усилие либо силу, с которой один объект действует на другой. Такое воздействие можно встретить повсеместно: это двери лифтов, троллейбуса, метро, ворот и тому подобное.
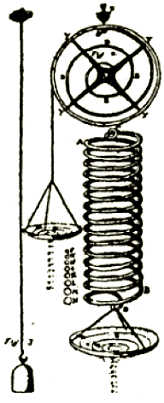
Необходимо отметить, что первым устройством, которое применялось для измерения силы, являлись весы. Впервые такие весы появились в 1726 году. Через столетие Ричард Солтер создал прибор, в котором применялась пружина с целью измерения воздействия силы. Благодаря грузу она растягивалась на некоторое расстояние, которое соответствовало его массе. Спустя некоторое время Ренье создал устройство, на котором имелся циферблат. В нем применялась кольцеобразная замкнутая пружина. Затем стали появляться конструкции других изобретателей в лице Томсона, Броуна и так далее. Современное устройство по своей конструкции недалеко ушли от этих приборов.
Динамометр может иметь разные конструкции, которые довольно сильно различаются по предназначению, исполнению, функциям, диапазону измерений и тому подобное. Данные устройства можно разделить по измеряемым усилиям, то есть их можно классифицировать по диапазону измерения: от долей ньютонов до 20 тысяч ньютонов. Если говорить о принципе действия, то данные приборы могут быть различного действия в зависимости от их конструктивного исполнения. При этом в некоторых устройствах могут применяться сразу несколько принципов действия.
Механические подразделяются на изделия рычажного и пружинного действия. Особенность пружинного прибора в том, что сила воздействует на пружину, вследствие чего она может растягиваться или сжиматься, что в свою очередь определяется направленностью приложения силового фактора. Пружина обладает упругостью, которая находится в прямой пропорциональности от приложенной силы, которую необходимо измерить. Поэтому ее можно определить и зафиксировать. При использовании рычажного устройства сила направлена на деформирование рычага, что в свою очередь позволяет определить ее параметры.
Электронное оснащается цифровым дисплеем, где высвечивается информация о прикладываемой силе. В этих устройствах основополагающим элементом является датчик. Его функции это преобразование деформации от действия силы в электросигнал. Он также имеет дополнительный датчик, усиливающий основной сигнал, идущий от первого датчика. С целью преобразования деформационного действия применяются разнообразные датчики сопротивления, которые построены на индуктивном, тензорезистивном, пьезоэлектрическом и частотном принципе действия.
В гидравлических устройствах применяется специальный цилиндр, в котором находится рабочая жидкость. Если внешняя сила оказывает определенное воздействие, то находящаяся в цилиндре жидкость выходит из него. В результате сила определяется объемом вытесненной жидкости. Данный объем находится в прямой зависимости от приложенной силы, что позволяет достаточно точно определить искомый параметр.
В зависимости от сферы применения могут быть и специфические устройства, позволяющие измерять силу воздействия, к примеру, медицинские. Такие устройства позволяют определить силу, степень функционирования мышц, выносливость, в том числе дают возможность следить за состоянием и восстановлением больного после получения травмы.
В отдельную категорию можно выделить кистевое устройство, при помощи него диагностируется сжимающая сила рук вследствие нарушения их функционирования. Тесты с применением данного устройства используются не только в медицинских целях, но также во многих организациях: это правоохранительные органы, Министерство чрезвычайных ситуаций, вооруженные силы, экспедиторские компании, организация боевых единоборств и профессионального спорта. Становое устройство применяется с целью определения сил мышц, которые предназначены для выпрямления туловища человека.
Образцовый динамометр представляет собой эталон, применяемый для определения сил в статике, чаще всего сил сжатия и растяжения во время ремонта испытательных устройств и установок. Данные приборы имеют малую зависимость от температуры окружающей среды. Их конструкция более сложна, что вызвано необходимостью получения независимости от внешних факторов. Так у них предусмотрена автоматическая компенсация искажений и имеются средства самодиагностики. Они обладают малыми габаритами, точностью и долговечностью. Для удобства пользования данные приборы имеют цифровую индикацию, удобный интерфейс и возможность подключения к персональному компьютеру.
Устройство
В большинстве случаев данные приборы имеют схожее устройство и принцип действия. Но все определяется конструкцией устройства.
Самый примитивный динамометр имеет следующее устройство:
При помощи крючка пружина крепится к основанию. Такое устройство очень просто в изготовлении, поэтому собрать его может любой человек, который знаком с основами физики. К примеру, для этого можно взять картонку, из которой следует вырезать основание размером 15 на 7 см. Далее потребуется пружина из металла диаметром проволоки 0,3-0,5 мм. Проволоку необходимо согнуть с одной стороны для закрепления к основанию. Для этого можно воспользоваться скотчем или степлером. С другой концы пружины следует сделать крючок.
Чтобы правильно нанести шкалу, потребуются небольшие мерные грузики. При помощи них на шкале проставляются данные по их весу, то есть на сколько пружина растягиваться, на такой длине и выставляются цифры. В результате появляется зависимость расставленных цифр на шкале от силы, которая прикладывается. Это значит, что можно измерить другую силу, которая будет приложена к пружине.
В электрических устройствах установлены пьезоэлектрические и т.п. датчики, которые работают посредством преобразования механической энергии в электрические сигналы. Данные сигналы усиливаются и фиксируются при помощи какого-либо элемента. К примеру, может быть использована шкала или цифровая индикация. Для возможности работы датчиков и цифровых устройств используются батарейки, аккумуляторы или электрическая сеть.
Принцип действия
Принцип работы электрических устройств основан на том, что датчик испытывает определенную деформацию, вследствие чего происходит изменение токов сопротивления. В результате электросигнал находится в прямой зависимости от деформации элемента. Дополнительному датчику лишь необходимо усилить сигнал и записать его, чтобы можно было снять параметры прикладываемой силы.
Динамометр механического действия работает несколько иначе. Главная его особенность в том, что при приложении силы пружина подвергается деформационному воздействию. Благодаря такому свойству можно измерить параметры деформационного воздействия, то есть силу, которая прикладывается к ней.
Гидравлические приборы способны демонстрировать более высокую точность, однако и конструкция у них более сложная. Принцип работы подобного устройства базируется на перемещении жидкости, расположенной в резервуаре, в момент приложения силы. Жидкость, которая была вытеснена по трубке, направляется к прибору, который и фиксирует ее объем.
Применение
Динамометр пружинного типа часто применяется с целью определения массы всевозможных грузов. Также их используют для определения показателей прочности сварочных швов и других соединений.
Динамометр может применяться для получения точных данных, параметров сил, к примеру:
Благодаря их функциональности приборы можно использовать в медицинских, строительных, промышленных и во многих других целях. Некоторые модели устройств способны измерять силу, которая может достигать 20 тысяч ньютонов.
Как выбрать
Сила упругости
Сила упругости широко используется в технике. Эта сила возникает в упругих телах при их деформации. Деформация – это изменение формы тела, под действием приложенных сил.
Виды деформации
Деформация – это изменение формы, или размеров тела.
Есть несколько видов деформации:
Деформация сдвига возникает, когда одни части тела сдвигаются относительно других его частей. Если подействовать на верхнюю часть картонного ящика, наполненного различными предметами, горизонтальной силой, то вызовем сдвиг верхней части ящика относительно его нижней части.
Сжатие или растяжение легко представить на примере прямоугольного куска тонкой резины. Такая деформация используется, к примеру, в резинках для одежды.
Примеры изгиба и кручения показаны на рисунке 1. Пластиковая линейка, деформированная изгибом, представлена на рис. 1а, а на рисунке 1б – эта же линейка, деформируемая кручением.
В деформируемом теле возникают силы, имеющие электромагнитную природу и препятствующие деформации.
Растяжение пружины
Рассмотрим подробнее деформацию растяжения на примере пружины.
Давайте прикрепим пружину к некоторой поверхности (рис. 2). На рисунке слева указана начальная длина \(L_<0>\) пружины.
Подвесим теперь к пружине груз. Пружина будет иметь длину \(L\), указанную на рисунке справа.
Сравним длину нагруженной пружины с длиной свободно висящей пружины.
\[ \large L_ <0>+ \Delta L = L \]
Найдем разницу (разность) между длинами свободно висящей пружины и пружины с грузом. Вычтем для этого из обеих частей этого уравнения величину \(L_<0>\).
\( L_ <0>\left(\text <м>\right) \) – начальная длина пружины;
\( L \left(\text <м>\right) \) – конечная длина растянутой пружины;
\( \Delta L \left(\text <м>\right) \) – кусочек длины, на который растянули пружину;
Величину \( \Delta L \) называют удлинением пружины.
Иногда рассчитывают относительное удлинение. Это относительное удлинение часто выражают десятичной дробью. Или дробью, в знаменателе которой находится число 100 — такую дробь называют процентом.
Примечание: Отношение – это дробь. Относительное – значит, дробное.
\( \varepsilon \) – это отношение (доля) растяжения пружины к ее начальной длине. Измеряют в процентах и называют относительным удлинением.
Расчет силы упругости
Если растягивать пружину вручную, мы можем заметить: чем больше мы растягиваем пружину, тем сильнее она сопротивляется.
Значит, с удлинением пружины связана сила, которая сопротивляется этому удлинению.
Конечно, если пружина окажется достаточно упругой, чтобы сопротивляться. Например, разноцветная пружина-игрушка (рис. 3), изготовленная из пластмассы, сопротивляться растяжению, увеличивающему ее длину в два раза, практически не будет.
Закон Гука
Английский физик Роберт Гук, живший во второй половине 17-го века, установил, что сила сопротивления пружины и ее удлинение связаны прямой пропорциональностью. Силу, с которой пружина сопротивляется деформации, он назвал \( F_<\text<упр>> \) силой упругости.
\[ \large \boxed< F_<\text<упр>> = k \cdot \Delta L >\]
Эту формулу назвали законом упругости Гука.
\( F_<\text<упр>> \left( H \right) \) – сила упругости;
\( \Delta L \left(\text <м>\right) \) – удлинение пружины;
\( \displaystyle k \left(\frac
Какие деформации называют малыми
Закон Гука применяют для малых удлинений (деформаций).
Если убрать деформирующую силу и тело вернется к первоначальной форме (размерам), то деформации называют малыми.
Если же тело к первоначальной форме не вернется – малыми деформации назвать не получится.
Как рассчитать коэффициент жесткости
Груз, прикрепленный к концу пружины, растягивает ее (рис. 4). Измерим удлинение пружины и составим силовое уравнение для проекции сил на вертикальную ось. Вес груза направлен против оси, а сила упругости, противодействующая ему – по оси.
Так как силы взаимно компенсируются, в правой части уравнения находится ноль.
\[ \large F_<\text<упр>> — m \cdot g = 0 \]
Подставим в это уравнение выражение для силы упругости
\[ \large k \cdot \Delta L — m \cdot g = 0 \]
Прибавим к обеим частям вес груза и разделим на измеренное изменение длины \(\Delta L \) пружины. Получим выражение для коэффициента жесткости:
Соединяем две одинаковые пружины
В задачниках по физике и пособиях для подготовки к ЕГЭ встречаются задачи, в которых одинаковые пружины соединяют последовательно, либо параллельно.
Параллельное соединение пружин
На рисунке 5а представлена свободно висящая пружина. Нагрузим ее (рис. 5б), она растянется на величину \(\Delta L\). Соединим две такие пружины параллельно и подвесим груз в середине перекладины (рис. 5в). Из рисунка видно, что конструкция из двух параллельных пружин под действием груза растянется меньше, нежели единственная такая пружина.
Сравним растяжение двух одинаковых пружин, соединенных параллельно, с растяжением одной пружины. К пружинам подвешиваем один груз весом \(mg\).
\[ \large k_ <1>\cdot \Delta L = m \cdot g \]
Две параллельные пружины:
\[ \large k_<\text<параллел>> \cdot \Delta L \cdot \frac<1><2>= m \cdot g \]
Так как правые части уравнений совпадают, левые части тоже будут равны:
\[ \large k_<\text<параллел>> \cdot \Delta L \cdot \frac<1><2>= k_ <1>\cdot \Delta L \]
Обе части уравнения содержат величину \(\Delta L \). Разделим обе части уравнения на нее:
Умножим обе части полученного уравнения на число 2:
Коэффициент жесткости \(k_<\text<параллел>>\) двух пружин, соединенных параллельно, увеличился вдвое, в сравнении с одной такой пружиной
Последовательное соединение пружин
Рисунок 6а иллюстрирует свободно висящую пружину. Нагруженная пружина (рис. 6б), растянута на длину \(\Delta L\). Теперь возьмем две такие пружины и соединим их последовательно. Подвесим груз к этим (рис. 6в) пружинам.
Практика показывает, что конструкция из двух последовательно соединенных пружин под действием груза растянется больше единственной пружины.
На каждую пружину в цепочке действует вес груза. Под действием веса пружина растягивается и передает далее по цепочке этот вес без изменений. Он растягивает следующую пружину. А та, в свою очередь, растягивается на такую же величину \(\Delta L\).
Примечание: Под действием силы пружина растягивается и передает эту растягивающую силу далее по цепочке без изменений
Сравним растяжение двух одинаковых последовательно соединенных пружин и растяжение единственной пружины. В обоих случаях к пружинам подвешиваем одинаковый груз весом \(mg\).
\[ \large k_ <1>\cdot \Delta L = m \cdot g \]
Две последовательные пружины:
\[ \large k_<\text<послед>> \cdot \Delta L \cdot 2 = m \cdot g \]
Так как правые части уравнений совпадают, левые части тоже будут равны:
\[ \large k_<\text<послед>> \cdot \Delta L \cdot 2 = k_ <1>\cdot \Delta L \]
Обе части уравнения содержат величину \(\Delta L \). Разделим обе части уравнения на нее:
Разделим обе части полученного уравнения на число 2:
Коэффициент жесткости \(k_<\text<послед>>\) двух пружин, соединенных последовательно, уменьшится вдвое, в сравнении с одной такой пружиной
Потенциальная энергия сжатой или растянутой пружины
Пружина сжатая (левая часть рис. 7), или растянутая (правая часть рис. 7) на длину \(\Delta L \) обладает потенциальной возможностью вернуться в первоначальное состояние и при этом совершить работу, например, по перемещению груза. В таких случаях физики говорят, что пружина обладает потенциальной энергией.
Эта энергия зависит от коэффициента жесткости пружины и от ее удлинения (или укорочения при сжатии).
Чем больше жесткость (упругость) пружины, тем больше ее потенциальная энергия. Увеличив удлинение пружины получим повышение ее потенциальной энергии по квадратичному закону:
\[ \large \boxed < E_
= \frac
\( E_
\left( \text <Дж>\right)\) – потенциальная энергия сжатой или растянутой пружины;
\( \Delta L \left(\text <м>\right) \) – удлинение пружины;
\( \displaystyle k \left(\frac