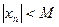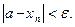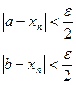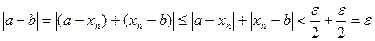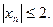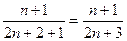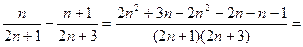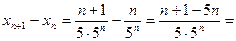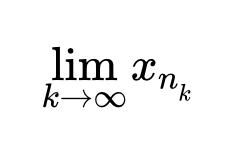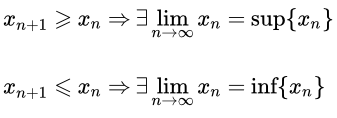доказать что последовательность является ограниченной если xn sin p

Ограниченные и неограниченные последовательности

Определение. Последовательность n> называется ограниченной, если существует такое число М>0, что для любого n верно неравенство:

т.е. все члены последовательности принадлежат промежутку (-М; M).

Определение. Последовательность (x_n) называется ограниченной сверху, если для любого n существует такое число М, что

Определение. Последовательность n>называется ограниченной снизу, если для любого n существует такое число М, что

Пример. n> = n – ограничена снизу <1, 2, 3,>.

Определение. Число а называется пределом последовательности n>, если для любого положительного e>0 существует такой номер N, что для всех n > N выполняется условие:

Это записывается: lim x_n = a.

В этом случае говорят, что последовательность n> сходится к а при n®¥.

Свойство: Если отбросить какое-либо число членов последовательности, то получаются новые последовательности, при этом если сходится одна из них, то сходится и другая.

Пример. Доказать, что предел последовательности lim .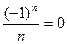

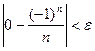
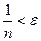
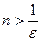
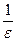
Пусть при n > N верно , т.е. . Это верно при , таким образом, если за N взять целую часть от , то утверждение, приведенное выше, выполняется.

Пример. Показать, что при n®¥ последовательность 3, 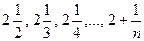имеет пределом число 2.

Очевидно, что существует такое число n, что 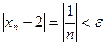, т.е. lim n> = 2.

Теорема. Последовательность не может иметь более одного предела.

Доказательство. Предположим, что последовательность n>имеет два предела a и b, не равные друг другу.

Тогда по определению существует такое число e >0, что

Запишем выражение:

А т.к. e- любое число, то 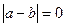, т.е. a = b. Теорема доказана.

Теорема. Если x_n ® a, то .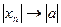

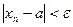
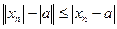
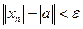
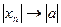
Доказательство. Из x_n ® a следует, что . В то же время:

, т.е. , т.е. . Теорема доказана.

Теорема. Если x_n ® a, то последовательность n> ограничена.

Следует отметить, что обратное утверждение неверно, т.е. из ограниченности последовательности не следует ее сходимость.

Например, последовательность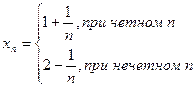не имеет предела, хотя

Монотонные последовательности

Определение:

1) Если x_n+1 > x_n для всех n, то последовательность возрастающая.

2) Если x_n+1 ³ x_n для всех n, то последовательность неубывающая.

n> = n – возрастающая и неограниченная.

Найдем член последовательности n₊₁> =

Найдем знак разности: n>-n₊₁> =

, т.к. nÎN, то знаменатель положительный при любом n.

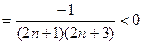
Таким образом, x_n+1 > x_n. Последовательность возрастающая, что и следовало доказать.

Найдем 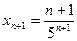. Найдем разность

Источник

Предел последовательности

п.1. Определение последовательности

С понятием «последовательность» мы уже познакомились, когда изучали прогрессии (см. §24 справочника для 9 класса). По определению:

Т.е., числовая последовательность – это некий набор чисел с присвоенными им порядковыми номерами. Это набор можно задать формулой, описанием или просто перечислением.

Например:
1) Формула \(y_n=\frac1n,\ n\in\mathbb\) задает бесконечную последовательность дробей:

2) Формула \(y_n=(-1)^n,\ n\in\mathbb\) задает бесконечную последовательность «прыгающих» единиц:

3) Рекуррентная формула \(y_1=1,\ y_2=1,\ y_(n+2)=y_(n+1)+y_n\) задает бесконечную последовательность чисел Фибоначчи:

4) Описание «число π точностью до \(10^<-n>\)» задает бесконечную последовательность все более «подробных» значений числа π:

Этот ряд можно также задать формулой \(y_n=\frac<[\pi\cdot 10^n]><10^n>\), где квадратные скобки обозначают целую часть от числа.

п.2. Предел последовательности

Поведение последовательности «на длинных дистанциях» может быть неочевидным. Чтобы лучше понять, возрастает или убывает заданный ряд чисел, ограничен ли он какой-либо величиной или уходит на бесконечность, проще всего построить график.

1) \(y_n=\frac1n\) Последовательность сходится к 0

2) \(y_n=(-1)^n\) Последовательность ни к чему не сходится

3) числа Фибоначчи \(y_1=1,\ y_2=1,\ y_=y_+y_n\) Последовательность уходит на бесконечность

4) приближения числа π Последовательность сходится к π

п.3. Как доказать сходимость последовательности к пределу?

И построим график (в логарифмическом масштабе):

Мы видим, что чем меньше ε, тем больше \(N_<\varepsilon>\). Но главное – мы всегда можем его указать.
Таким образом, мы доказали, что действительно \(\lim_\frac<1>=0\)
Ведь для любого сколь угодно малого \(\varepsilon\gt 0\) мы можем указать такой номер \(N_<\varepsilon>=\left[\frac1\varepsilon-4\right]+1\), начиная с которого, для всех членов последовательности с номерами \(n\geq N_<\varepsilon>\) разность \(\left|\frac<1>-0\right|\), т.е. эти члены не выйдут за переделы ε окрестности предела b=0.

Построенный график интересен еще и тем, что показывает одно из важных практических применений логарифмов: если разбросы по шкалам очень велики, отличаются на порядки, то графики удобней строить в десятичных логарифмах.
Такие графики часто можно увидеть у физиков-ядерщиков, копающих вглубь, от нанометров до планковских длин; или у астрономов, всматривающихся вдаль, от тысяч километров до гигапарсек.

п.4. Ограниченные и неограниченные последовательности

п.5. Как доказать неограниченность последовательности?

Таким образом, мы доказали, что действительно \(\lim_n^2=+\infty\)
Ведь для любого сколь угодно большого \(M\gt 0\) мы можем указать такой номер \(N_M=[\sqrt]\), начиная с которого, для всех членов последовательности с номерами \(n\geq N_M,\ y_n=n^2\gt M\), т.е. члены последовательности становятся ещё больше.

п.6. Примеры

Таким образом, для любого сколь угодно малого ε>0 найдется номер в последовательности \(N_<\varepsilon>=\left[\frac12\left(\frac<5><2\varepsilon>+3\right)\right]+1\), начиная с которого
\(\left|\frac<3-2n>+\frac12\right|\lt\varepsilon,\ n\geq N_<\varepsilon>\geq 2\).
Что и требовалось доказать.

Показанный приём с усилением неравенства часто применяется в математическом анализе. Найденное \(N_<\varepsilon>\) немного больше «точного» значения, которое следует из исходной дроби \(\frac<3(3n^2+n+1)>\), но наша задача в том, чтобы обоснованно построить любое выражение для стартового номера \(N_<\varepsilon>\) в зависимости от ε.
Если найденный номер будет немного больше исходного – не страшно; главное, чтобы он 1) был обоснован; 2) гарантировал размещение всех последующих \(y_n,\ n\geq N_<\varepsilon>\) в ε окрестности предела b.

Таким образом, для любого сколь угодно малого ε>0 найдется номер в последовательности \(N_<\varepsilon>=\left[\frac<1><3\sqrt<\varepsilon>>\right]\), начиная с которого \(\left|\frac<3n^2+n+1>-\frac13\right|\lt\varepsilon,\ n\geq N_<\varepsilon>\geq 3\).
Что и требовалось доказать.

Таким образом, для любого сколь угодно малого ε>0 найдется номер в последовательности \(N_<\varepsilon>=\left[-\log_3\varepsilon\right]\), начиная с которого \(\left|\frac<3^n+1><3^n>-1\right|\lt\varepsilon,\ n\geq N_<\varepsilon>\).
Что и требовалось доказать.

Таким образом, для любого сколь угодно малого ε>0 найдется номер в последовательности \(N_<\varepsilon>=\left[\left(\frac<1><5\varepsilon>-1\right)^2\right]\), начиная с которого \(\left|\frac<\sqrt><5\sqrt+1>-\frac15\right|\lt\varepsilon,\ n\geq N_<\varepsilon>\).
Что и требовалось доказать.

Пример 2. Используя определения неограниченной последовательности, докажите, что:
a) \( \lim_2^n=+\infty \)
По условию: \(y_n=2^n\)
Записываем неравенство \(|y_n|\gt M\):
\begin 2^n\gt M\Rightarrow n\gt \log_2M\\ N_M=\left[\log_2M\right]+1 \end Например:

Таким образом, для любого сколь угодно большого \(M\gt 0\) мы можем указать такой номер \(N_M=\left[\log_2M\right]+1\), начиная с которого, для всех членов последовательности с номерами \(n\geq N_M,\ y_n=2^n\gt M\).
Что и требовалось доказать.

Таким образом, для любого сколь угодно большого \(M\gt 0\) мы можем указать такой номер \(N_M=\left[M^2\right]\), начиная с которого, для всех членов последовательности с номерами \(n\geq N_M,\ y_n=\sqrt\gt M\).
Что и требовалось доказать.

Источник

Подпоследовательности и частичные пределы последовательностей

Определение подпоследовательности

Свойства подпоследовательностей

Свойство 3 является следствием свойств 1 и 2.

Частичный предел последовательности

Произвольная последовательность может иметь конечное или бесконечное число частичных пределов ⇑.

5. Свойство частичного предела последовательности
Точка является частичным пределом последовательности тогда и только тогда, когда в любой окрестности точки a содержится бесконечное число членов последовательности.
Доказательство ⇓

Верхний и нижний частичные пределы

Рассмотрим множество частичных пределов последовательности. Эта теорема утверждает, что верхняя и нижняя грани этого множества являются ее элементами. То есть множество частичных пределов последовательности замкнуто, оно содержит свою границу. Для произвольного множества это может не выполняться. Например, для открытого интервала не существует наибольшего и наименьшего элемента, поскольку и верхняя грань b и нижняя a не принадлежит этому множеству.

Если последовательность не ограничена сверху, то ее верхний частичный предел равен плюс бесконечности:
.
Соответственно, если последовательность не ограничена снизу, то
.

Если последовательность ограничена, то ее верхний и нижний частичные пределы конечны.

8. Теорема о неравенстве между верхним и нижним частичными пределами
Верхний и нижний частичные пределы последовательности удовлетворяют неравенству:
.
Частичные пределы равны друг другу тогда и только тогда, когда существует предел последовательности:
.
Доказательство ⇓

9. Связь верхних и нижних пределов между последовательностями n> и <–x_n>.
Имеет место очевидное равенство:
.

10. Свойства верхних и нижних пределов суммы последовательностей
Верхний и нижний частичные пределы от суммы последовательностей удовлетворяют следующим неравенствам:
;
,
где последовательности и ограничены.
Доказательство ⇓

11. Свойство верхних пределов произведения последовательностей
Пусть последовательность сходится к конечному положительному числу:
.
И пусть – любая последовательность. Тогда
.
Отсюда
.
Доказательство ⇓

Применяя равенство
,
можно получить другие подобные соотношения.

Доказательство свойств и теорем

Далее перечислены определения и свойства, которые мы будем использовать при доказательстве свойств подпоследовательностей.

1. Свойство подпоследовательностей сходящейся последовательности

2. Свойство последовательности, все подпоследовательности которой сходятся к одному числу

5. Свойство частичного предела последовательности

Все свойства ⇑ Точка является частичным пределом последовательности тогда и только тогда, когда в любой окрестности точки a содержится бесконечное число членов последовательности.

Возьмем произвольную окрестность точки a : ⇑. В качестве первого члена подпоследовательности возьмем любой член последовательности, принадлежащий этой окрестности.

6. Теорема о существовании верхнего и нижнего частичных пределов

В этом случае точка является верхним частичным пределом последовательности.

Пусть последовательность ограничена сверху и при этом любой отрезок содержит только конечное число членов последовательности.

Поскольку мы выбирали самые правые отрезки с бесконечным числом членов, то точка c является верхним частичным пределом последовательности.

7. Свойство верхнего и нижнего частичных пределов

8. Теорема о неравенстве между верхним и нижним частичными пределами

Все свойства ⇑ Верхний и нижний частичные пределы последовательности удовлетворяют неравенству:
.
Частичные пределы равны друг другу тогда и только тогда, когда существует предел последовательности:
.

10. Свойства верхних и нижних пределов суммы последовательностей

Все свойства ⇑ Верхний и нижний частичные пределы от суммы последовательностей удовлетворяют следующим неравенствам:
;
,
где последовательности и ограничены.

Докажем второе неравенство:
.
Умножим первое неравенство на – 1 :
.
Применим свойство 8 ⇑:
.

11. Свойство верхних пределов произведения последовательностей

Все свойства ⇑ Пусть последовательность сходится к конечному положительному числу:
.
И пусть – любая последовательность. Тогда
.
Отсюда
.

Из (10.1) и (10.2) следует, что
.
Свойство доказано.

Использованная литература:
С.М. Никольский. Курс математического анализа. Том 1. Москва, 1983.

Источник

Последовательность

Последовательность
Нужно определить, является ли последовательность бесконечно большой, неограниченной, ограниченной.

Последовательность
Доказать что последовательность \sum_^\frac<1> расходится при помощи критерия Коши.

последовательность и ее подпоследовательности
существует например последовательность xn=\lg x * sin(\pi *x/2) предел ее подпоследовательность.

ограниченная последовательность
может ли быть ограниченной последовательностью сумма двух неограниченных последовательностей?

Допустим что выполняется условие 1).
1. Выберем M₁=1 и для него найдём n₁ такое что x_n1>M₁=1.
2. Следующее M₂ выбираем равное x_n1+1. Тогда опять же найдется n₂ такое что x_n2>M₂=2.
3. Следующее M₃ выбираем равное x_n2+1. Тогда опять же найдется n₃ такое что x_n3>M₃=3.
.
Таким образом, мы построили последовательность x_nk, k=1, 2, 3. которая является подпоследовательностью x_n и является бесконечно большой, потому что она больше чем бесконечно большая последовательность 1, 2, 3.

Для 2) и 3) доказательство аналогичное.

Помощь в написании контрольных, курсовых и дипломных работ здесь.

Пределы и Последовательность
Здравствуйте, я списал с доски решение профессора, и не могу понять, что за трюк. У меня другой.

Источник

Теорема Вейерштрасса о пределе монотонной последовательности

Теорема Вейерштрасса о пределе монотонной последовательности

Любая монотонная ограниченная последовательность < x_n > имеет конечный предел, равный точной верней границе, sup < x_n > для неубывающей и точной нижней границе, inf < x_n > для невозрастающей последовательности.
Любая монотонная неограниченная последовательность имеет бесконечный предел, равный плюс бесконечности, для неубывающей и минус бесконечности, для невозрастающей последовательности.

Доказательство

1) Пусть последовательность является неубывающей ограниченной последовательностью.

Поскольку последовательность ограничена, то она имеет конечную точную верхнюю границу
.
Это означает, что:

Поскольку последовательность ограничена, то она имеет конечную точную нижнюю границу
.
Это означает следующее:

Теперь рассмотрим неограниченные последовательности.
3) Пусть последовательность является неограниченной неубывающей последовательностью.

Поскольку последовательность неубывающая, то при имеем:
.
Здесь мы также использовали (3.2).

4) Наконец рассмотрим случай, когда является неограниченной невозрастающей последовательностью.

Поскольку последовательность невозрастающая, то при имеем:
.

Пример решения задачи

Представим последовательность в виде рекуррентных формул:
,
.

Поскольку последовательность возрастает и ограничена сверху, то она является ограниченной последовательностью. Поэтому, по теореме Вейерштрасса, она имеет предел.

Источник