доказать что предел не существует

Предел последовательности и функции. Теоремы о пределах

Определение пределов последовательности и функции, свойства пределов, первый и второй замечательные пределы, примеры.

Постоянное число а называется пределом последовательности n>, если для любого сколь угодно малого положительного числа ε > 0 существует номер N, что все значения x_n, у которых n>N, удовлетворяют неравенству

Понятие предел функции является обобщением понятия предел последовательности, так как предел последовательности можно рассматривать как предел функции x_n = f(n) целочисленного аргумента n.

Определение 1. Постоянное число А называется предел функции f(x) при x→ a, если для всякой последовательности n> значений аргумента, стремящейся к а, соответствующие им последовательности n)> имеют один и тот же предел А.

Это определение называют определением предела функции по Гейне, или “на языке последовательностей”.

Используются на практике и следствия формулы (6.11):

(6.12)

(6.13)

(6.14)

в частности предел,

Eсли x → a и при этом x > a, то пишут x →a + 0. Если, в частности, a = 0, то вместо символа 0+0 пишут +0. Аналогично если x→a и при этом x и называются соответственно предел справа и предел слева функции f(x) в точке а. Чтобы существовал предел функции f(x) при x→ a необходимо и достаточно, чтобы . Функция f(x) называется непрерывной в точке x₀, если предел

(6.15)

Условие (6.15) можно переписать в виде:

то есть возможен предельный переход под знаком функции, если она непрерывна в данной точке.

Если равенство (6.15) нарушено, то говорят, что при x = x_o функция f(x) имеет разрыв. Рассмотрим функцию y = 1/x. Областью определения этой функции является множество R, кроме x = 0. Точка x = 0 является предельной точкой множества D(f), поскольку в любой ее окрестности, т.е. в любом открытом интервале, содержащем точку 0, есть точки из D(f), но она сама не принадлежит этому множеству. Значение f(x_o)= f(0) не определено, поэтому в точке x_o = 0 функция имеет разрыв.

Функция f(x) называется непрерывной справа в точке x_o, если предел

и непрерывной слева в точке x_o, если предел

Непрерывность функции в точке x_o равносильна ее непрерывности в этой точке одновременно и справа и слева.

Для того, чтобы функция была непрерывна в точке x_o, например, справа, необходимо, во-первых, чтобы существовал конечный предел , а во-вторых, чтобы этот предел был равен f(x_o). Следовательно, если хотя бы одно из этих двух условий не выполняется, то функция будет иметь разрыв.

1. Если предел существует и не равен f(x_o), то говорят, что функция f(x) в точке x_o имеет разрыв первого рода, или скачок.

Функция, непрерывная в каждой точке промежутка [a,b], называется непрерывной в [a,b]. Непрерывная функция изображается сплошной кривой.

Ко второму замечательному пределу приводят многие задачи, связанные с непрерывным ростом какой-либо величины. К таким задачам, например, относятся: рост вклада по закону сложных процентов, рост населения страны, распад радиоактивного вещества, размножение бактерий и т.п.

100×(1 +1/10) 10 ≈ 259 (ден. ед.),

100×(1+1/100) 100 ≈ 270 (ден. ед.),

100×(1+1/1000) 1000 ≈271 (ден. ед.).

При безграничном сокращении сроков присоединения процентов наращенный капитал не растет беспредельно, а приближается к некоторому пределу, равному приблизительно 271. Более чем в 2,71 раз капитал, положенный под 100% годовых, увеличиться не может, даже если бы наросшие проценты присоединялись к капиталу каждую секунду, потому что предел

Пример 3.1. Пользуясь определением предела числовой последовательности, доказать, что последовательность x_n =(n-1)/n имеет предел, равный 1.

Пример 3.2. Найти предел последовательности, заданной общим членом .

Пример 3.3. . Найти .

Решение.

Здесь мы воспользовались теоремой о пределе степени: предел степени равен степени от предела основания.

Пример 3.4. Найти ().

Решение. Применять теорему предел разности нельзя, поскольку имеем неопределенность вида ∞-∞. Преобразуем формулу общего члена:

Пример 3.6. Доказать, что предел не существует.

Если x_n= p n, то sin x_n= sin ( p n) = 0 при всех n и предел Если же
x_n=2 p n+ p /2, то sin x_n= sin(2 p n+ p /2) = sin p /2 = 1 для всех n и следовательно предел . Таким образом, не существует.

Пример 3.7 Найти предел

Решение. Имеем: . Обозначим t = 5x. При x →0 имеем: t →0. Применяя формулу (3.10), получим .

Пример 3.8. Вычислить предел .

Решение. Обозначим y=π-x. Тогда при x→π, y→0. Имеем:

sin 3x = sin 3(π-y) = sin(3π-3y) = sin 3y.

_Предел

Пример 3.9. Найти предел .

Решение. Обозначим arcsin x=t. Тогда x=sin t и при x→0, t→0. .

Пример 3.10. Найти 1) ;

2) ;

3) .

1) Применяя теорему 1 предел разности и предел произведения, находим предел знаменателя: .

Предел знаменателя не равен нулю, поэтому, по теореме 1 предел частного, получаем:

.

2) Здесь числитель и знаменатель стремятся к нулю, т.е. имеет место неопределенность вида 0/0. Теорема о пределе частного непосредственно неприменима. Для “раскрытия неопределенности” преобразуем данную функцию. Разделив числитель и знаменатель на x-2, получим при x ≠ 2 равенство:

Так как предел , то, по теореме предел частного, найдем

3. Числитель и знаменатель при x → ∞ являются бесконечно большими функциями. Поэтому теорема предел частного непосредственно не применима. Разделим числитель и знаменатель на x 2 и к полученной функции применим теорему предел частного:

.

Пример 3.11. Найти предел .

Решение. Здесь числитель и знаменатель стремятся к нулю:, x-9→0, т.е. имеем неопределенность вида .

Преобразуем данную функцию, умножив числитель и знаменатель на неполный квадрат суммы выражения , получим

.

Пример 3.12. Найти предел .

Решение.

Источник

Как доказать что предела не существует

Определение пределов последовательности и функции, свойства пределов, первый и второй замечательные пределы, примеры.

Постоянное число а называется пределом последовательности _n>, если для любого сколь угодно малого положительного числа ε > 0 существует номер N, что все значения x_n, у которых n>N, удовлетворяют неравенству

Последовательность, имеющая предел, называется сходящейся, в противном случае — расходящейся.

Понятие предел функции является обобщением понятия предел последовательности, так как предел последовательности можно рассматривать как предел функции x_n = f(n) целочисленного аргумента n.

Пусть дана функция f(x) и пусть a — предельная точка области определения этой функции D(f), т.е. такая точка, любая окрестность которой содержит точки множества D(f), отличные от a. Точка a может принадлежать множеству D(f), а может и не принадлежать ему.

Определение 1. Постоянное число А называется предел функции f(x) при x→ a, если для всякой последовательности _n> значений аргумента, стремящейся к а, соответствующие им последовательности _n)> имеют один и тот же предел А.

Это определение называют определением предела функции по Гейне, или “на языке последовательностей”.

Определение 2. Постоянное число А называется предел функции f(x) при x→a, если, задав произвольное, как угодно малое положительное число ε, можно найти такое δ >0 (зависящее от ε), что для всех x, лежащих в ε-окрестности числа а, т.е. для x, удовлетворяющих неравенству
0 » 2.7 — основание натурального логарифма. Формулы (6.10) и (6.11) носят название первый замечательного предело и второй замечательный предел.

Используются на практике и следствия формулы (6.11):

(6.12)

(6.13)

(6.14)

в частности предел,

Eсли x → a и при этом x > a, то пишут x →a + 0. Если, в частности, a = 0, то вместо символа 0+0 пишут +0. Аналогично если x→a и при этом x и называются соответственно предел справа и предел слева функции f(x) в точке а. Чтобы существовал предел функции f(x) при x→ a необходимо и достаточно, чтобы . Функция f(x) называется непрерывной в точке x₀, если предел

(6.15)

Условие (6.15) можно переписать в виде:

то есть возможен предельный переход под знаком функции, если она непрерывна в данной точке.

Если равенство (6.15) нарушено, то говорят, что при x = x_o функция f(x) имеет разрыв. Рассмотрим функцию y = 1/x. Областью определения этой функции является множество R, кроме x = 0. Точка x = 0 является предельной точкой множества D(f), поскольку в любой ее окрестности, т.е. в любом открытом интервале, содержащем точку 0, есть точки из D(f), но она сама не принадлежит этому множеству. Значение f(x_o)= f(0) не определено, поэтому в точке x_o = 0 функция имеет разрыв.

Функция f(x) называется непрерывной справа в точке x_o, если предел

и непрерывной слева в точке x_o, если предел

Непрерывность функции в точке x_o равносильна ее непрерывности в этой точке одновременно и справа и слева.

Для того, чтобы функция была непрерывна в точке x_o, например, справа, необходимо, во-первых, чтобы существовал конечный предел , а во-вторых, чтобы этот предел был равен f(x_o). Следовательно, если хотя бы одно из этих двух условий не выполняется, то функция будет иметь разрыв.

1. Если предел существует и не равен f(x_o), то говорят, что функция f(x) в точке x_o имеет разрыв первого рода, или скачок.

Функция, непрерывная в каждой точке промежутка [a,b], называется непрерывной в [a,b]. Непрерывная функция изображается сплошной кривой.

Ко второму замечательному пределу приводят многие задачи, связанные с непрерывным ростом какой-либо величины. К таким задачам, например, относятся: рост вклада по закону сложных процентов, рост населения страны, распад радиоактивного вещества, размножение бактерий и т.п.

Рассмотрим пример Я. И. Перельмана, дающий интерпретацию числа e в задаче о сложных процентах. Число e есть предел . В сбербанках процентные деньги присоединяются к основному капиталу ежегодно. Если присоединение совершается чаще, то капитал растет быстрее, так как в образовании процентов участвует большая сумма. Возьмем чисто теоретический, весьма упрощенный пример. Пусть в банк положено 100 ден. ед. из расчета 100 % годовых. Если процентные деньги будут присоединены к основному капиталу лишь по истечении года, то к этому сроку 100 ден. ед. превратятся в 200 ден.ед. Посмотрим теперь, во что превратятся 100 ден. ед., если процентные деньги присоединять к основному капиталу каждые полгода. По истечении полугодия 100 ден. ед. вырастут в 100 ×1,5 = 150, а еще через полгода — в 150× 1,5 = 225 (ден. ед.). Если присоединение делать каждые 1/3 года, то по истечении года 100 ден. ед. превратятся в 100 × (1 +1/3) 3 ≈ 237 (ден. ед.). Будем учащать сроки присоединения процентных денег до 0,1 года, до 0,01 года, до 0,001 года и т.д. Тогда из 100 ден. ед. спустя год получится:

100×(1 +1/10) 10 ≈ 259 (ден. ед.),

100×(1+1/100) 100 ≈ 270 (ден. ед.),

100×(1+1/1000) 1000 ≈271 (ден. ед.).

При безграничном сокращении сроков присоединения процентов наращенный капитал не растет беспредельно, а приближается к некоторому пределу, равному приблизительно 271. Более чем в 2,71 раз капитал, положенный под 100% годовых, увеличиться не может, даже если бы наросшие проценты присоединялись к капиталу каждую секунду, потому что предел

Пример 3.1. Пользуясь определением предела числовой последовательности, доказать, что последовательность x_n =(n-1)/n имеет предел, равный 1.

Пример 3.2. Найти предел последовательности, заданной общим членом .

Пример 3.3. . Найти .

Решение.

Здесь мы воспользовались теоремой о пределе степени: предел степени равен степени от предела основания.

Пример 3.4. Найти ().

Решение. Применять теорему предел разности нельзя, поскольку имеем неопределенность вида ∞-∞. Преобразуем формулу общего члена:

Пример 3.6. Доказать, что предел не существует.

Решение. Пусть x₁, x₂. x_n. — последовательность, для которой
. Как ведет себя последовательность _n)> = при различных x_n→ ∞

Если x_n= p n, то sin x_n= sin ( p n) = 0 при всех n и предел Если же
x_n=2 p n+ p /2, то sin x_n= sin(2 p n+ p /2) = sin p /2 = 1 для всех n и следовательно предел . Таким образом, не существует.

Пример 3.7 Найти предел

Пример 3.8. Вычислить предел .

Решение. Обозначим y=π-x. Тогда при x→π, y→0. Имеем:

sin 3x = sin 3(π-y) = sin(3π-3y) = sin 3y.

sin 4x = sin 4(π-y) = sin (π4-4y)= — sin 4y.

_Предел

Пример 3.9. Найти предел .

Решение. Обозначим arcsin x=t. Тогда x=sin t и при x→0, t→0. .

Пример 3.10. Найти 1) ;

2) ;

3) .

1) Применяя теорему 1 предел разности и предел произведения, находим предел знаменателя: .

Предел знаменателя не равен нулю, поэтому, по теореме 1 предел частного, получаем:

.

2) Здесь числитель и знаменатель стремятся к нулю, т.е. имеет место неопределенность вида 0/0. Теорема о пределе частного непосредственно неприменима. Для “раскрытия неопределенности” преобразуем данную функцию. Разделив числитель и знаменатель на x-2, получим при x ≠ 2 равенство:

Так как предел , то, по теореме предел частного, найдем

3. Числитель и знаменатель при x &rarr ∞ являются бесконечно большими функциями. Поэтому теорема предел частного непосредственно не применима. Разделим числитель и знаменатель на x 2 и к полученной функции применим теорему предел частного:

.

Пример 3.11. Найти предел .

Решение. Здесь числитель и знаменатель стремятся к нулю:, x-9→0, т.е. имеем неопределенность вида .

Преобразуем данную функцию, умножив числитель и знаменатель на неполный квадрат суммы выражения , получим

.

Пример 3.12. Найти предел .

Решение.

Пример 3.6. Доказать, что предел lim sin(x) при x-> ∞ не существует.

В этой статье мы расскажем, что из себя представляет предел функции. Сначала поясним общие моменты, которые очень важны для понимания сути этого явления.

Понятие предела

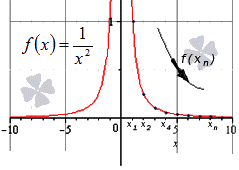
Если мы не можем определить ни конечное, ни бесконечное значение, это значит, что такого предела не существует. Примером этого случая может быть предел от синуса на бесконечности.

Что такое предел функции

В этом пункте мы объясним, как найти значение предела функции в точке и на бесконечности. Для этого нам нужно ввести основные определения и вспомнить, что такое числовые последовательности, а также их сходимость и расходимость.

При x → ∞ предел функции f ( x ) является бесконечным, если последовательность значений для любой бесконечно большой последовательности аргументов будет также бесконечно большой (положительной или отрицательной).

Решение

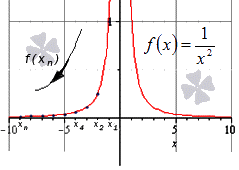
Далее мы запишем то же самое, но для бесконечно большой отрицательной последовательности.

Здесь тоже видно монотонное убывание к нулю, что подтверждает верность данного в условии равенства:

Ответ: Верность данного в условии равенства подтверждена.

Решение

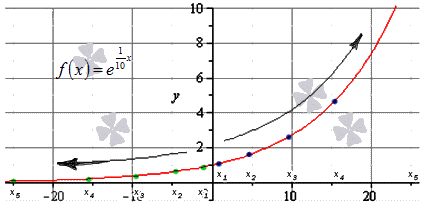
Мы видим, что данная последовательность бесконечно положительна, значит, f ( x ) = lim x → + ∞ e 1 10 x = + ∞

Наглядно решение задачи показано на иллюстрации. Синими точками отмечена последовательность положительных значений, зелеными ­ – отрицательных.

Перейдем к методу вычисления предела функции в точке. Для этого нам нужно знать, как правильно определить односторонний предел. Это пригодится нам и для того, чтобы найти вертикальные асимптоты графика функции.

Теперь сформулируем, что такое предел функции справа.

Теперь мы разъясним данные определения, записав решение конкретной задачи.

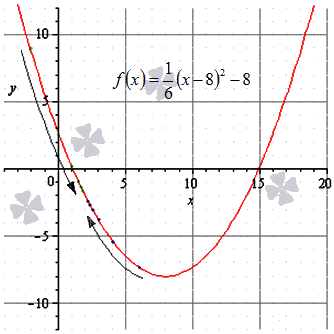
Докажите, что существует конечный предел функции f ( x ) = 1 6 ( x — 8 ) 2 — 8 в точке x 0 = 2 и вычислите его значение.

Решение

Значения функции в этой последовательности будут выглядеть так:

Чтобы более глубоко изучить теорию пределов, советуем вам прочесть статью о непрерывности функции в точке и основных видах точек разрыва.

Источник