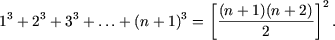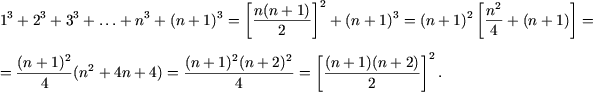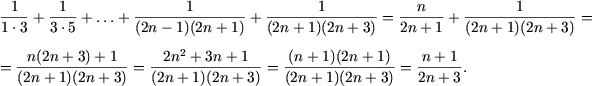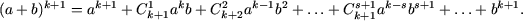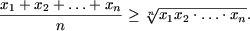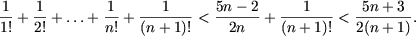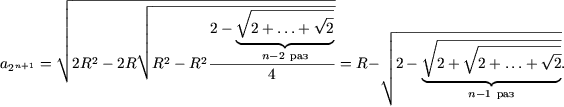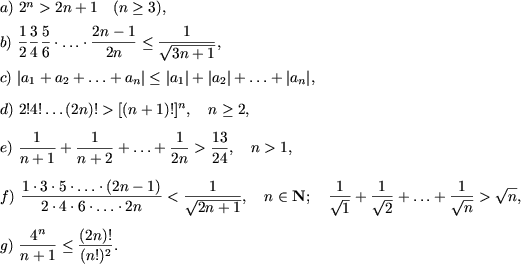доказать методом математической индукции что для любого
Метод математической индукции для чайников
Метод полного перебора конечного числа случаев, исчерпывающих все возможности, называется полной индукцией. Этот метод имеет крайне ограниченную область применения в математике, так как обычно математические утверждения касаются бесконечного множества объектов (например, натуральных чисел, простых чисел, квадратов и т.п.) и перебрать их невозможно.
Основы метода математической индукции
Доказательство с помощью метода математической индукции проводится в два этапа:
Метод математической индукции применяется в разных типах задач:
Ниже вы найдете примеры решения задач, иллюстрирующие применение метода математической индукции, а также ссылки на полезные сайты и учебник и небольшой видеоурок по ММИ.
Математическая индукция: задачи и решения
Доказательство кратности и делимости
$$a_n = 2n^3+3n^2+7n, \quad b=6.$$
Доказательство равенств и неравенств
Задача 5. Доказать равенство
Задача 6. Доказать методом математической индукции:
Задача 7. Доказать неравенство:
Задача 8. Доказать утверждение методом математической индукции:
Задача 9. Доказать неравенство:
Вычисление сумм
Задача 11. Доказать методом математической индукции:
Задача 12. Найдите сумму
Заказать решение
Полезные ссылки о ММИ
Кратенький видеоурок о ММИ
Доказать методом математической индукции что для любого
Применяя метод математической индукции, доказать, что для любого натурального n справедливы следующие равенства:
а) ;
б) .
а) При n = 1 равенство справедливо. Предполагая справедливость равенства при n, покажем справедливость его и при n + 1. Действительно,
что и требовалось доказать.
б) При n = 1 справедливость равенства очевидна. Из предположения справедливости его при n следует
т. е. утверждение справедливо и при n + 1.
Пример 1. Доказать следующие равенства
Решение. a) При n = 1 равенство примет вид 
Таким образом, согласно методу математической индукции, исходное равенство справедливо для любого натурального n.
Используя предположение индукции, получим
Таким образом, P(n + 1) истинно и, следовательно, требуемое равенство доказано.
Замечание 3. Этот пример можно решить (аналогично предыдущему) без использования метода математической индукции.
c) При n = 1 равенство истинно: 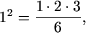
d) При n = 1 равенство справедливо: 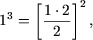
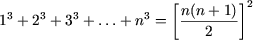
e) Утверждение P(1) справедливо: 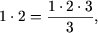
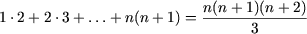
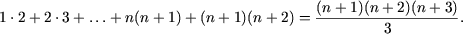
Следовательно, исходное равенство имеет место для любого натурального n.
f) P(1) справедливо: 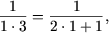
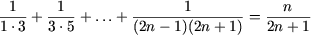
Действительно, учитывая, что P(n) имеет место, получим
Таким образом, равенство доказано.
g) При n = 1 имеем a + b = b + a и, следовательно, равенство справедливо.
Пусть формула бинома Ньютона справедлива при n = k, то есть,
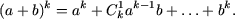
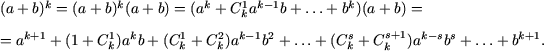
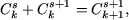
Пример 2. Доказать неравенства
Решение. a) При n = 1 получаем истинное неравенство
Таким образом, если P(n) истинно, то и P(n + 1) истинно, следовательно, согласно принципу математической индукции, неравенство Бернулли справедливо.
Рассмотрим следующие два случая:
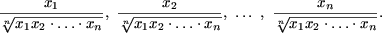
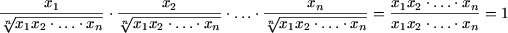
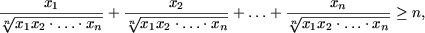
sin 2n a + cos 2n a ≤ 1 и покажем, что имеет место P ( n + 1). Действительно, sin 2(n + 1) a + cos 2(n + 1) a = sin 2n a ·sin 2 a + cos 2n a ·cos 2 a 2n a + cos 2n a ≤ 1 (если sin 2 a ≤ 1, то cos 2 a 2 a ≤ 1, то sin 2 a n О N sin 2n a + cos 2n ≤ 1 и знак равенства достигается лишь при n = 1.
e) При n = 1 утверждение справедливо: 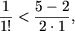
Допустим, что 
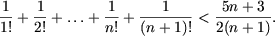
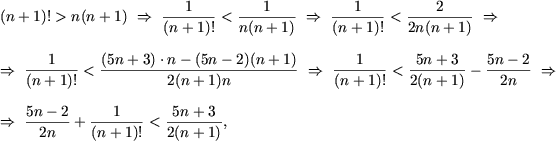
Поскольку при n > 10 имеем 
Пример 3. Доказать, что для любого n О N

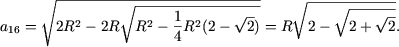
 | (2) |
Как ранее было показано при n = 1, что эта формула справедлива. Пусть (2) выполняется при n = k. Вычислим 
Замечание. Из (2) следует, что длина окружности равна
I. Доказать равенства
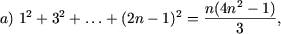 |
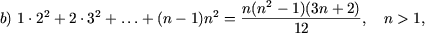 |
 |
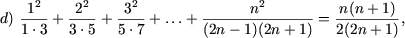 |
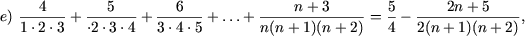 |
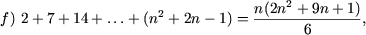 |
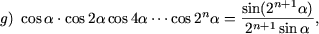 |
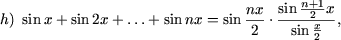 |
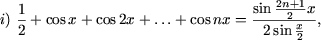 |
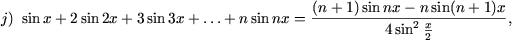 |
 |
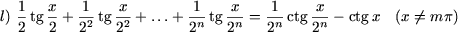 |
 |
II. Доказать неравенства
III. Доказать, что при любом натуральном n число an делится на b
IV. Показать, что 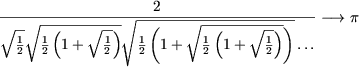
VI. Пусть даны n произвольных квадратов. Доказать, что эти квадраты могут быть разрезаны так, чтобы из получившихся частей можно было образовать квадрат.
Метод математической индукции
В первом пункте мы разберем основные понятия, потом рассмотрим основы самого метода, а затем расскажем, как с его помощью доказывать равенства и неравенства.
Понятия индукции и дедукции
Для начала рассмотрим, что такое вообще индукция и дедукция.
Индукция – это переход от частного к общему, а дедукция наоборот – от общего к частному.
В целом можно сказать, что с помощью индуктивных рассуждений можно получить множество выводов из одного известного или очевидного рассуждения. Математическая индукция позволяет нам определить, насколько справедливы эти выводы.
В чем заключается метод математической индукции
В основе этого метода лежит одноименный принцип. Он формулируется так:
Применение метода математической индукции осуществляется в 3 этапа:
Как применять метод математической индукции при решении неравенств и уравнений
Возьмем пример, о котором мы говорили ранее.
Решение
Как мы уже знаем, для применения метода математической индукции надо выполнить три последовательных действия.
Мы можем представить k + 1 в качестве суммы первых членов исходной последовательности и k + 1 :
S k + 1 = S k + 1 k + 1 ( k + 2 )
Теперь выполняем нужные преобразования. Нам потребуется выполнить приведение дроби к общему знаменателю, приведение подобных слагаемых, применить формулу сокращенного умножения и сократить то, что получилось:
S k + 1 = S k + 1 k + 1 ( k + 2 ) = k k + 1 + 1 k + 1 ( k + 2 ) = = k ( k + 2 ) + 1 k + 1 ( k + 2 ) = k 2 + 2 k + 1 k + 1 ( k + 2 ) = ( k + 1 ) 2 k + 1 ( k + 2 ) = k + 1 k + 2
Таким образом, мы доказали равенство в третьем пункте, выполнив все три шага метода математической индукции.
Ответ: предположение о формуле S n = n n + 1 является верным.
Возьмем более сложную задачу с тригонометрическими функциями.
Решение
cos 2 1 = cos 2 α sin 2 1 + 1 α 2 1 sin 2 α = sin 4 α 2 sin 2 α = 2 sin 2 α · cos 2 α 2 sin 2 α = cos 2 α
Согласно тригонометрической формуле,
Ответ: На этом тождество можно считать доказанным. Мы успешно применили для этого метод математической индукции. Точно так же мы можем доказать справедливость формулы бинома Ньютона.
Пример решения задачи на доказательство неравенства с применением этого метода мы привели в статье о методе наименьших квадратов. Прочтите тот пункт, в котором выводятся формулы для нахождения коэффициентов аппроксимации.
Применение метода математической индукции к решению задач на делимость натуральных чисел
Рубрика: Математика: алгебра и начала анализа, геометрия
Дата публикации: 02.05.2015 2015-05-02
Статья просмотрена: 9530 раз
Библиографическое описание:
Баданин, А. С. Применение метода математической индукции к решению задач на делимость натуральных чисел / А. С. Баданин, М. Ю. Сизова. — Текст : непосредственный // Юный ученый. — 2015. — № 2 (2). — С. 84-86. — URL: https://moluch.ru/young/archive/2/128/ (дата обращения: 19.12.2021).
В математических олимпиадах часто встречаются достаточно трудные задачи на доказательство делимости натуральных чисел. Перед школьниками возникает проблема: как найти универсальный математический метод, позволяющий решать подобные задачи?
Оказывается, большинство задач на доказательство делимости можно решать методом математической индукции, но в школьных учебниках уделяется очень мало внимания этому методу, чаще всего приводится краткое теоретическое описание и разбирается несколько задач.
Метод математической индукции мы находим в теории чисел. На заре теории чисел математики открыли многие факты индуктивным путем: Л. Эйлер и К. Гаусс рассматривали подчас тысячи примеров, прежде чем подметить числовую закономерность и поверить в нее. Но одновременно они понимали, сколь обманчивыми могут быть гипотезы, прошедшие «конечную» проверку. Для индуктивного перехода от утверждения, проверенного для конечного подмножества, к аналогичному утверждению для всего бесконечного множества необходимо доказательство. Такой способ предложил Блез Паскаль, который нашел общий алгоритм для нахождения признаков делимости любого целого числа на любое другое целое число (трактат «О характере делимости чисел).
Метод математической индукции используется, чтобы доказать путем рассуждений истинность некоего утверждения для всех натуральных чисел или истинность утверждения начиная с некоторого числа n.
Решение задач на доказательство истинности некоторого утверждения методом математической индукции состоит из четырех этапов (рис. 1):
Рис. 1. Схема решения задачи
1. Базис индукции. Проверяют справедливость утверждения для наименьшего из натуральных чисел, при котором утверждение имеет смысл.
2. Индукционное предположение. Предполагаем, что утверждение верно для некоторого значения k.
3. Индукционный переход. Доказываем, что утверждение справедливо для k+1.
4. Вывод. Если такое доказательство удалось довести до конца, то, на основе принципа математической индукции можно утверждать, что утверждение верно для любого натурального числа n.
Рассмотрим применение метода математической индукции к решению задач на доказательство делимости натуральных чисел.
Пример 1. Доказать, что число 5 
1) Проверим, что эта формула верна при n = 1: число 
2) Пусть эта формула верна для n = k, т. е. число 
3) Докажем, что формула верна и для n = k + 1, т. е.

4) Оба условия принципа математической индукции выполнены, следовательно, предложение истинно при всех значениях n.
Пример 2. Доказать, что сумма кубов трех последовательных натуральных чисел делится на 9.
Докажем утверждение: «Для любого натурального числа n выражение n 3 +(n+1) 3 +(n+2) 3 кратно 9.
1) Проверим, что эта формула верна при n = 1: 13+23+33=1+8+27=36 кратно 9.
2) Пусть эта формула верна для n = k, т. е. k 3 +(k+1) 3 +(k+2) 3 кратно 9.
3) Докажем, что формула верна и для n = k + 1, т. е. (k+1) 3 +(k+2) 3 +(k+3) 3 кратно 9. (k+1) 3 +(k+2) 3 +(k+3) 3 =(k+1) 3 +(k+2) 3 + k 3 + 9k 2 +27 k+ 27=(k 3 +(k+1) 3 +(k+2) 3 )+9(k 2 +3k+ 3).
Полученное выражение содержит два слагаемых, каждое из которых делится на 9, таким образом, сумма делится на 9.
4) Оба условия принципа математической индукции выполнены, следовательно, предложение истинно при всех значениях n.
Пример 3. Доказать, что при любом натуральном n число 3 2n+1 +2 n+2 делится на 7.
1) Проверим, что эта формула верна при n = 1: 3 2*1+1 +2 1+2 = 3 3 +2 3 =35, 35 кратно 7.
2) Пусть эта формула верна для n = k, т. е. 3 2 k +1 +2 k +2 делится на 7.
3) Докажем, что формула верна и для n = k + 1, т. е.
4) Оба условия принципа математической индукции выполнены, следовательно, предложение истинно при всех значениях n.
Многие задачи на доказательство в теории делимости натуральных чисел удобно решать с применением метода математической индукции, можно даже сказать, что решение задач данным методом вполне алгоритмизировано, достаточно выполнить 4 основных действия. Но универсальным этот метод назвать нельзя, т. к. присутствуют и недостатки: во-первых, доказывать можно только на множестве натуральных чисел, а во-вторых, доказывать можно только для одной переменной.
Для развития логического мышления, математической культуры этот метод является необходимым инструментом, ведь ещё великий русский математик А. Н. Колмогоров говорил: «Понимание и умение правильно применять принцип математической индукции, является хорошим критерием логической зрелости, которая совершенно необходима математику».
1. Виленкин Н. Я. Индукция. Комбинаторика. — М.: Просвещение, 1976. — 48 с.
2. Генкин Л. О математической индукции. — М., 1962. — 36 с.
3. Соломинский И. С. Метод математической индукции. — М.: Наука, 1974. — 63с.
4. Шарыгин И. Ф. Факультативный курс по математике: Решение задач: Учеб.пособие для 10 кл. сред.шк. — М.: Просвещение, 1989. — 252 с.
5. Шень А. Математическая индукция. — М.: МЦНМО,2007.- 32 с.
math4school.ru
Метод математической индукции
Немного теории
Индукция есть метод получения общего утверждения из частных наблюдений. В случае, когда математическое утверждение касается конечного числа объектов, его можно доказать, проверяя для каждого объекта. Например, утверждение: «Каждое двузначное чётное число является суммой двух простых чисел,» – следует из серии равенств, которые вполне реально установить:
Метод доказательства, при котором проверяется утверждение для конечного числа случаев, исчерпывающих все возможности, называют полной индукцией. Этот метод применим сравнительно редко, поскольку математические утверждения касаются, как правило, не конечных, а бесконечных множеств объектов. Например, доказанное выше полной индукцией утверждение о четных двузначных числах является лишь частным случаем теоремы: «Любое четное число является суммой двух простых чисел». Эта теорема до сих пор ни доказана, ни опровергнута.
Математическая индукция – метод доказательства некоторого утверждения для любого натурального n основанный на принципе математической индукции: «Если утверждение верно для n=1 и из справедливости его для n=k вытекает справедливость этого утверждения для n=k+1, то оно верно для всех n». Способ доказательства методом математической индукции заключается в следующем:
1) база индукции: доказывают или непосредственно проверяют справедливость утверждения для n=1 (иногда n=0 или n=n0);
2) индукционный шаг (переход): предполагают справедливость утверждения для некоторого натурального n=k и, исходя из этого предположения, доказывают справедливость утверждения для n=k+1.
Задачи с решениями
Проведём доказательство методом математической индукции.
База индукции. Если n=1, то А(1)=3 3 +2 3 =35 и, очевидно, делится на 7.
Предположение индукции. Пусть А(k) делится на 7.
Индукционный переход. Докажем, что А(k+1) делится на 7, то есть справедливость утверждения задачи при n=k.
А(k+1)=3 2(k+1)+1 +2 (k+1)+2 =3 2k+1 ·3 2 +2 k+2 ·2 1 =3 2k+1 ·9+2 k+2 ·2=
Последнее число делится на 7, так как представляет собой разность двух целых чисел, делящихся на 7. Следовательно, 3 2n+1 +2 n+2 делится на 7 при любом натуральном n.
Введём обозначение: аi=2 3 i +1.
аk+1=2 3 k+1 +1=(2 3 k ) 3 +1=(2 3 k +1)( 2 3 k ·2 –2 3 k +1)=3 k+1 ·m·((2 3 k +1) 2 –3·2 3 k )=3 k+1 ·m·((3 k+1 ·m) 2 –3·2 3 k )=
=3 k+2 ·m·(3 2k+1 ·m 2 –2 3 k ).
Следовательно, утверждение доказано для любого натурального n.
3. Известно, что х+1/x – целое число. Доказать, что х n +1/х n – так же целое число при любом целом n.
Введём обозначение: аi=х i +1/х i и сразу отметим, что аi=а–i, поэтому дальше будем вести речь о натуральных индексах.
Заметим: а1 – целое число по условию; а2 – целое, так как а2=(а1) 2 –2; а0=2.
Предположим, что аk целое при любом натуральном k не превосходящем n. Тогда а1·аn – целое число, но а1·аn=аn+1+аn–1 и аn+1=а1·аn–аn–1. Однако, аn–1, согласно индукционному предположению, – целое. Значит, целым является и аn+1. Следовательно, х n +1/х n – целое число при любом целом n, что и требовалось доказать.
4. Доказать, что при любом натуральном n большем 1 справедливо двойное неравенство
Воспользуемся методом математической индукции.
При n=2 неравенство верно. Действительно,
Если неравенство верно при n=k, то при n=k+1 имеем
Неравенство доказано для любого натурального n > 1.
6. На плоскости дано n окружностей. Доказать, что при любом расположении этих окружностей образуемую ими карту можно правильно раскрасить двумя красками.
Воспользуемся методом математической индукции.
При n=1 утверждение очевидно.
Предположим, что утверждение справедливо для любой карты, образованной n окружностями, и пусть на плоскости задано n+1 окружностей. Удалив одну из этих окружностей, мы получим карту, которую в силу сделанного предположения можно правильно раскрасить двумя красками (смотрите первый рисунок из приведённых ниже).
Восстановим затем отброшенную окружность и по одну сторону от нее, например внутри, изменим цвет каждой области на противоположный (смотрите второй рисунок). Легко видеть, что при этом мы получим карту, правильную раскрашенную двумя красками, но только теперь уже при n+1 окружностях, что и требовалось доказать.
7. Выпуклый многоугольник будем называть «красивым», если выполняются следующие условия:
1) каждая его вершина окрашена в один из трёх цветов;
2) любые две соседние вершины окрашены в разные цвета;
3) в каждый из трёх цветов окрашена, по крайней мере, одна вершина многоугольника.
Доказать, что любой красивый n-угольник можно разрезать не пересекающимися диагоналями на «красивые» треугольники.
Воспользуемся методом математической индукции.
База индукции. При наименьшем из возможных n=3 утверждение задачи очевидно: вершины «красивого» треугольника окрашены в три разных цвета и никакие разрезы не нужны.
Предположение индукции. Допустим, что утверждение задачи верно для любого «красивого» n-угольника.
Индукционный шаг. Рассмотрим произвольный «красивый» (n+1)-угольник и докажем, используя предположение индукции, что его можно разрезать некоторыми диагоналями на «красивые» треугольники. Обозначим через А1, А2, А3, … Аn, Аn+1 – последовательные вершины (n+1)-угольника. Если в какой-либо из трёх цветов окрашена лишь одна вершина (n+1)-угольника, то, соединив эту вершину диагоналями со всеми не соседними с ней вершинами, получим необходимое разбиение (n+1)-угольника на «красивые» треугольники.
Если в каждый из трёх цветов окрашены не менее двух вершин (n+1)-угольника, то обозначим цифрой 1 цвет вершины А1, а цифрой 2 цвет вершины А2. Пусть k – такой наименьший номер, что вершина Аk окрашена в третий цвет. Понятно, что k > 2. Отсечём от (n+1)-угольника диагональю Аk–2Аk треугольник Аk–2 Аk–1Аk. В соответствии с выбором числа k все вершины этого треугольника окрашены в три разных цвета, то есть этот треугольник «красивый». Выпуклый n-угольник А1А2 … Аk–2АkАk+1 … Аn+1, который остался, также, в силу индуктивного предположения, будет «красивым», а значит разбивается на «красивые» треугольники, что и требовалось доказать.
8. Доказать, что в выпуклом n-угольнике нельзя выбрать больше n диагоналей так, чтобы любые две из них имели общую точку.
Проведём доказательство методом математической индукции.
Докажем более общее утверждение: в выпуклом n-угольнике нельзя выбрать больше n сторон и диагоналей так, чтобы любые две из них имели общую точку. При n = 3 утверждение очевидно. Допустим, что это утверждение верно для произвольного n-угольника и, используя это, докажем его справедливость для произвольного (n+1)-угольника.
Допустим, что для (n+1)-угольника это утверждение неверно. Если из каждой вершины (n+1)-угольника выходит не больше двух выбранных сторон или диагоналей, то всего их выбрано не больше чем n+1. Поэтому из некоторой вершины А выходит хотя бы три выбранных стороны или диагонали AB, AC, AD. Пусть АС лежит между АВ и AD. Поскольку любая сторона или диагональ, которая выходит из точки С и отличная от СА, не может одновременно пересекать АВ и AD, то из точки С выходит только одна выбранная диагональ СА.
Отбросив точку С вместе с диагональю СА, получим выпуклый n-угольник, в котором выбрано больше n сторон и диагоналей, любые две из которых имеют общую точку. Таким образом, приходим к противоречию с предположением, что утверждение верно для произвольного выпуклого n-угольника.
Итак, для (n+1)-угольника утверждение верно. В соответствии с принципом математической индукции утверждение верно для любого выпуклого n-угольника.
9. В плоскости проведено n прямых, из которых никакие две не параллельны и никакие три не проходят через одну точку. На сколько частей разбивают плоскость эти прямые.
С помощью элементарных рисунков легко убедится в том, что одна прямая разбивает плоскость на 2 части, две прямые – на 4 части, три прямые – на 7 частей, четыре прямые – на 11 частей.
Обозначим через N(n) число частей, на которые n прямых разбивают плоскость. Можно заметить, что
Естественно предположить, что
или, как легко установить, воспользовавшись формулой суммы n первых членов арифметической прогрессии,
Докажем справедливость этой формулы методом математической индукции.
Для n=1 формула уже проверена.
Сделав предположение индукции, рассмотрим k+1 прямых, удовлетворяющих условию задачи. Выделим из них произвольным образом k прямых. По предположению индукции они разобьют плоскость на 1+ k(k+1)/2 частей. Оставшаяся (k+1)-я прямая разобьётся выделенными k прямыми на k+1 частей и, следовательно, пройдёт по (k+1)-й части, на которые плоскость уже была разбита, и каждую из этих частей разделит на 2 части, то есть добавится ещё k+1 часть. Итак,
что и требовалось доказать.
10. В выражении х1:х2: … :хn для указания порядка действий расставляются скобки и результат записывается в виде дроби:
Прежде всего ясно, что в полученной дроби х1 будет стоять в числителе. Почти столь же очевидно, что х2 окажется в знаменателе при любой расстановке скобок (знак деления, стоящий перед х2, относится либо к самому х2, либо к какому-либо выражению, содержащему х2 в числителе).
Докажем это утверждение по индукции.
При n=3 можно получить 2 дроби:
так что утверждение справедливо.
Предположим, что оно справедливо при n=k и докажем его для n=k+1.
Пусть выражение х1:х2: … :хk после некоторой расстановки скобок записывается в виде некоторой дроби Q. Если в это выражение вместо хk подставить хk:хk+1, то хk окажется там же, где и было в дроби Q, а хk+1 будет стоять не там, где стояло хk (если хk было в знаменателе, то хk+1 окажется в числителе и наоборот).
Теперь докажем, что можно добавить хk+1 туда же, где стоит хk. В дроби Q после расстановки скобок обязательно будет выражение вида q:хk, где q – буква хk–1 или некоторое выражение в скобках. Заменив q:хk выражением (q:хk):хk+1=q:(хk·хk+1), мы получим, очевидно, ту же самую дробь Q, где вместо хk стоит хk·хk+1.
Задачи без решений
1. Доказать, что при любом натуральном n:
а) число 5 n –3 n +2n делится на 4;
б) число n 3 +11n делится на 6;
в) число 7 n +3n–1 делится на 9;
г) число 6 2n +19 n –2 n+1 делится на 17;
д) число 7 n+1 +8 2n–1 делится на 19;
е) число 2 2n–1 –9n 2 +21n–14 делится на 27.
2. Докажите, что (n+1)·(n+2)· … ·(n+n) = 2 n ·1·3·5·…·(2n–1).
3. Доказать неравенство |sin nx| n|sin x| для любого натурального n.
4. Найдите натуральные числа a, b, c, которые не делятся на 10 и такие, что при любом натуральном n числа a n + b n и c n имеют одинаковые две последние цифры.
5. Доказать, что если n точек не лежат на одной прямой, то среди прямых, которые их соединяют, не менее чем n различных.