докажите что биссектрисы треугольника пересекаются в одной точке

Общие сведения

Треугольник — геометрическая фигура, состоящая из трех точек, не лежащих на одной прямой, и отрезков, соединяющих их. Точки имеют другое название — вершины. Обозначается треугольник символом Δ, после которого идут 3 латинских буквы. Например, ΔMNO. Допускается использовать и русские литеры, но злоупотреблять этим не стоит.

В высших учебных заведениях преподаватели требуют от студентов международное обозначение. Кроме того, большинство программных продуктов и онлайн-сервисов воспринимают только латинские символы.

Существует определенная классификация Δ, на основании которой доказываются теоремы, выводятся формулы, свойства и решаются задачи. В последнем случае следует правильно производить идентификацию, чтобы избежать ошибок при расчетах.

Классификация треугольников

Необходимо отметить, что Δ различаются между собой по некоторым критериям.

Они бывают нескольких типов:

В первом случае стороны фигуры не равны между собой. Чтобы идентифицировать прямоугольный треугольник, необходимо рассмотреть его углы. Если один из них является прямым (равен 90 градусам), такая фигура называется прямоугольной. В третьем виде основным критерием считается наличие двух, равных между собой сторон.

В равностороннем треугольнике все стороны равны между собой. Математики его называют «правильным». Он обладает важным свойством — вокруг него можно описать окружность. Пятый тип определяет наличие тупого угла, градусная мера которого больше 90. Если фигура является остроугольной, это значит, что все 3 его угла меньше 90, т. е. являются острыми.

Один треугольник может относиться к нескольким типам. Например, прямоугольный Δ может быть равнобедренным на основании свойства геометрии: если Δ является равнобедренным, то углы (∠), образованные боковыми сторонами с основанием, равны между собой. В этом случае их градусные меры эквивалентны 45, поскольку сумма ∠ любого Δ составляет 180. Следовательно, 180 — 90 = 2k, где неизвестная величина «к» соответствует углу при основании.

Решая уравнение, можно получить искомое значение угла: k = 45. Исходя из вычислений, треугольник является прямоугольным и равнобедренным.

Дополнительные элементы

У любого Δ существуют определенные дополнительные элементы, необходимые при построении чертежей или схематических рисунков, доказательства теорем и решения задач по геометрии.

К ним относятся:

Биссектриса — отрезок (прямая), проходящий через вершину Δ и делящий угол на 2 равные части. Медиана — единственный отрезок для каждой вершины, соединяющий ее с серединой стороны, на которую он опущен.

Высотой является перпендикуляр, опущенный из вершины на противоположную сторону.

В равнобедренном и равностороннем треугольниках биссектриса является медианой и высотой. В последнем случае их можно провести всего 3.

Теорема о биссектрисах

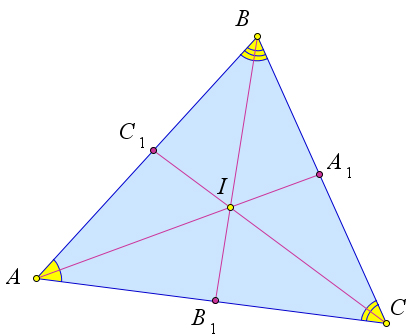
Теорема о биссектрисах треугольника звучит таким образом: в любом Δ биссектрисы пересекаются только в одной точке — инцентре фигуры. Для доказательства нужно построить произвольный ΔКLМ, а затем следовать по такому алгоритму:

Необходимо доказать, что третья биссектриса (МV), проведенная из вершины М, проходит через точку W. Это делается таким образом:

Далее следует рассмотреть ∠М. Следовательно, что координата точки W равноудалена от вершины М. На основании признака биссектрисы, W лежит на МV, поскольку W — точка пересечения биссектрис треугольника КLМ. Утверждение доказано.

Свойства и соотношения

На основании теоремы о биссектрисах Δ были получены некоторые важные свойства, которые рекомендуется применять при решении задач и доказательства других утверждений:

При решении задач нужно находить их длину (L).

Для удобства необходимо обозначить стороны таким образом: КМ = d, КL = e и LМ = f, чтобы воспользоваться следующими формулами через известные параметры треугольника:

Соотношения позволяют найти не только длины Lk, Lm и Ll, но и другие параметры треугольников. Следует отметить, что углы во второй группе формул соответствуют биссектрисам, исходящим из них.

Таким образом, для решения задач на нахождение длины биссектрис необходимо знать теорию, доказательство теоремы, свойства, а также основные соотношения.

Источник

Биссектриса угла

Когда-то древние астрономы и математики открыли очень много интересных свойств биссектрисы угла треугольников и других фигур.

Эти знания сильно упростили жизнь людей. Стало легче строить, считать расстояния, даже корректировать стрельбу из пушек…

Нам же знание этих свойств поможет решить некоторые задания ЕГЭ!

Биссектриса угла — коротко о главном

Биссектриса угла — это линия, делящая угол пополам.

Биссектриса угла – это геометрическое место точек, равноудаленых от сторон угла.

Биссектриса треугольника – это отрезок биссектрисы угла треугольника, соединяющий вершину этого угла с точкой на противолежащей стороне.

Теорема 1. Три биссектрисы в треугольнике пересекаются в одной точке, и эта точка – центр вписанной в треугольник окружности.

Теорема 2. В равнобедренном треугольнике биссектриса, проведённая из вершины к основанию, является также и медианой, и высотой.

Теорема 3. Биссектриса угла параллелограмма отсекает равнобедренный треугольник.

Теорема 4. Биссектрисы внутреннего и внешнего углов треугольника перпендикулярны.

Теорема 5. Биссектрисы односторонних углов параллелограмма и трапеции пересекаются под прямым углом.

Теорема 6. Отношение отрезков, на которые биссектриса делит противоположную сторону, такое же, как и отношение двух сторон, между которыми эта биссектриса прошла.

А теперь подробнее…

Определение биссектрисы угла

Помнишь шутку: «Биссектриса это крыса, которая бегает по углам и делит угол пополам»?

Так вот, настоящее определение биссектрисы угла очень похоже на эту шутку — биссектриса действительно делит пополам угол (а не отрезок, например):

Биссектриса угла – это линия, делящая угол пополам.

Или еще вот такое определение биссектрисы:

Биссектриса угла – это геометрическое место точек, равноудаленых от сторон угла.

А вот определение биссектрисы треугольника:

Биссектриса треугольника – это отрезок биссектрисы угла треугольника, соединяющий вершину этого угла с точкой на противолежащей стороне.

Тебе встретилась в задаче биссектриса? Постарайся применить одно (а иногда можешь и несколько) из следующих потрясающих свойств.

Биссектриса равнобедренного треугольника

Биссектриса равнобедренного треугольника, проведенная к основанию, является и медианой, и высотой.

Но представляешь, это ещё не всё. Верна ещё и обратная теорема:

Если в треугольнике биссектриса, проведённая из какого-то угла, совпадает с медианой или с высотой, то этот треугольник равнобедренный.

Мы скоро докажем обе этих теоремы, а пока твердо запомни:

Биссектриса совпадает с высотой и медианой только в равнобедренном треугольнике!

Зачем же это твердо запоминать? Как это может помочь?

А вот представь, что у тебя задача:

Дано: \( AB=5,

Найти: \( \displaystyle BC. \)

Ты тут же соображаешь, \(\displaystyle BD \) биссектриса и, о чудо, она разделила сторону \( \displaystyle AC \) пополам! (по условию…).

Если ты твердо помнишь, что так бывает только в равнобедренном треугольнике, то делаешь вывод, что AB=BC и значит, пишешь ответ: BC=5.

Здорово, правда? Конечно, не во всех задачах будет так легко, но знание обязательно поможет!

Доказательство теорем о совпадении биссектрисы с медианой и высотой в равнобедренном треугольнике

Почему в случае с равнобедренным треугольником биссектриса оказывается одновременно и медианой и высотой?

Смотри: у \( \triangle ABL \) и \( \triangle CBL \) равны стороны \( AB \) и \( BC \), сторона \( BL \) у них вообще общая и \( \angle 1=\angle 2\). (\( BL \) – биссектриса!)

И вот, получилось, что два треугольника имеют по две равные стороны и угол между ними.

Вспоминаем первый признак равенства треугольников (не помнишь, загляни в тему «Треугольник») и заключаем, что \( \triangle ABL=\triangle CBL \), а значит \( AL \)= \( CL \) и \( \angle 3=\angle 4 \).

\( AL \) = \( CL \) – это уже хорошо – значит, \( BL \) оказалась медианой.

А вот что такое \( \angle 3=\angle 4 \)?

Читать далее…

Чтобы пользоваться учебником ЮКлэва без ограничений, зарегистрируйтесь один раз:

Будет немного сложнее, но пока мы отвлечемся на термины — повторим что такое биссектриса, медиана и высота, чем они похожи и чем они отличаются.

Биссектриса, медиана, высота — определения и отличия

Кстати, а помнишь ли ты все эти термины? Чем они отличаются друг от друга?

Если нет, не страшно. Сейчас разберемся.

Чем биссектриса, медиана и высота похожи между собой?

Биссектриса, медиана и высота – все они «выходят» из вершины треугольника и упираются в противоположную сторону и «что-то делают» либо с углом из которого выходят, либо с противоположной стороной.

Чем биссектриса, медиана и высота отличаются между собой?

Вернемся к нашим баранам — к свойствам биссектрисы…

Угол между биссектрисами любого треугольника

B \( \triangle ABC \)проведем две биссектрисы \( AO \)и \( OC \).

Они пересеклись. Какой же угол получился у точки \( O \)?

Применим этот потрясающий факт. С одной стороны, из \( \triangle ABC \):

\( \angle A+\angle B+\angle C=180<>^\circ \), то есть \( \angle B=180<>^\circ \text< >-\text< >\left( \angle A+\angle C \right) \).

Теперь посмотрим на \( \triangle AOC \):

\( \angle 2+\angle 6+\angle 3=180<>^\circ \)

Но биссектрисы, биссектрисы же!

Значит \( \left( \triangle AOC \right) \)

Теперь через буквы

Получилось, что угол между биссектрисами двух углов зависит только от третьего угла!

Ну вот, две биссектрисы мы посмотрели. А что, если их три?! Пересекутся ли они все в одной точке?

Источник

Инструменты пользователя

Инструменты сайта

Содержание

Четыре замечательные точки треугольника

Определение

Окружность называется вписанной в многоугольник, если она касается всех его сторон. Многоугольник в таком случае называется описанным.

Определение

Окружность называется описанной около многоугольника, если она проходит через все его вершины. Многоугольник в таком случае называется вписанным в данную окружность.

Определение

Точка пересечения медиан треугольника называется центроидом или центром масс.

Замечение

Медианы треугольника пересекаются в одной точке по теореме.

Теорема о биссектрисе, как ГМТ

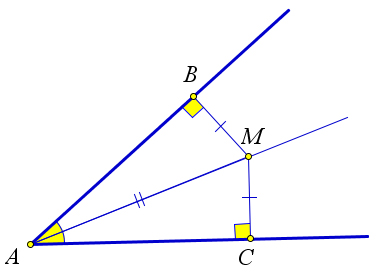
Биссектриса неразвернутого угла – это геометрическое место точек, равноудаленных от его сторон.

Доказательство

Докажем, что любая точка, принадлежащая биссектрисе равноудалена от сторон этого угла.

Обратно: докажем, что если точка равноудалена от сторон угла, то она лежит на биссектрисе.

Теорема

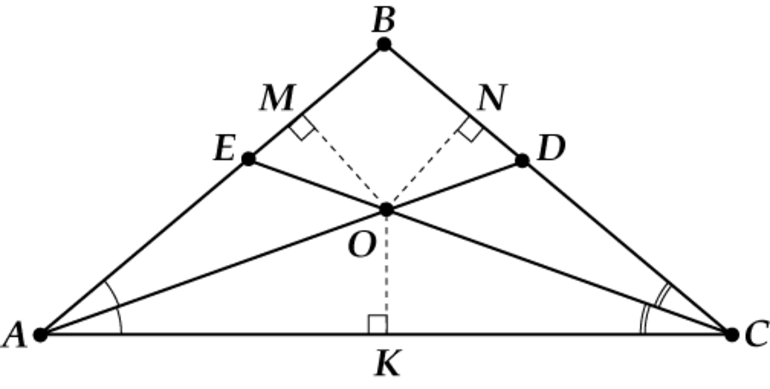
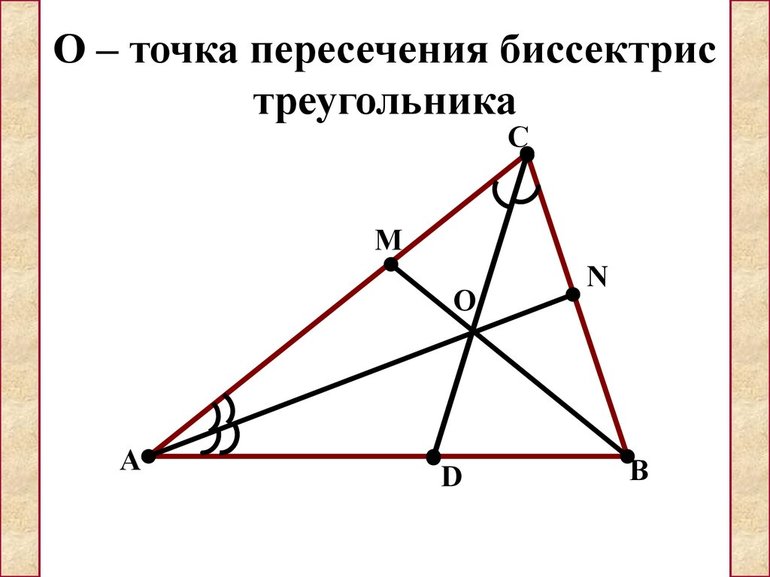
Биссектрисы треугольника пересекаются в одной точке.

Доказательство

Первый способ.

Второй способ.

Докажем, что все биссектрисы пересекаются в одной точке.

Следствие

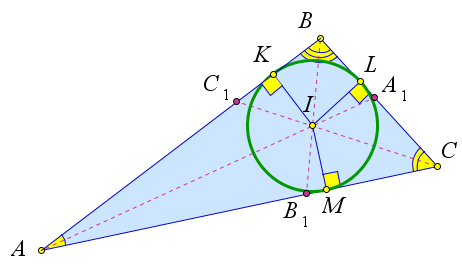
В любой треугольник можно вписать окружность, центром которой будет являться точка пересечения его биссектрис. Такая окружность единственна.

Доказательство

Докажем, что такая окружность единственна.

В самом деле, допустим, что в треугольник можно вписать две окружности.

Следовательно, эти окружности совпадают.

Следствие

Если все биссектрисы выпуклого многоугольника пересекаются в одной точке, то в него можно вписать окружность, центром которой будет точка пересечения биссектрис.

Доказательство

Если все биссектрисы пересекаются в одной точке, то эта точка будет равноудалена от всех её сторон, то есть перпендикуляры к сторонам многоугольника будут равны, а окружность с центром в этой точке и с радиусом, равным расстоянию от точки пересечения биссектрис до стороны, будет касаться всех сторон.

Теорема о серединном перпендикуляре, как ГМТ

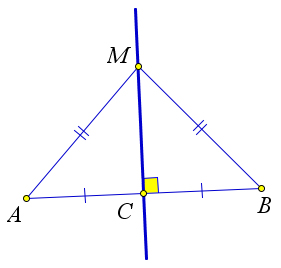
Серединный перпендикуляр к отрезку – это геометрическое место точек, равноудаленных от концов отрезка.

Доказательство

Докажем, что любая точка, принадлежащая серединному перпендикуляру, равноудалена от сторон.

Обратно, докажем, что любая точка равноудалённая от сторон, принадлежит серединному перпендикуляру.

Следствие

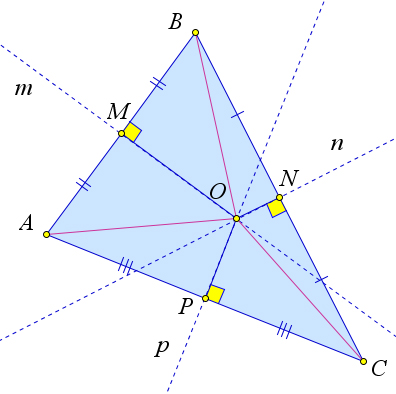
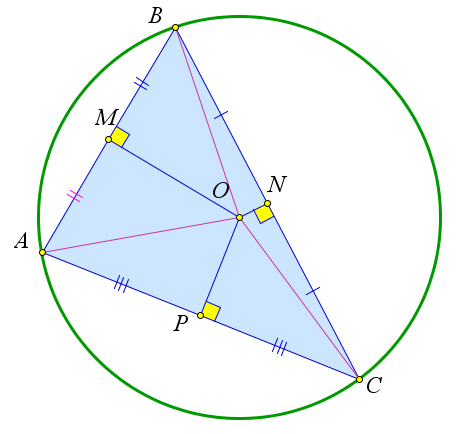
Все серединные перпендикуляры к сторонам треугольника пересекаются в одной точке.

Доказательство

Докажем, что эти серединные перпендикуляры пересекаются в одной точке.

Следствие

Около любого треугольника можно описать окружность, центром которой будет точка пересечения серединных перпендикуляров к его сторонам. Такая окружность единственна.

Доказательство

Докажем, что такая окружность единственна.

Предположим, что в треугольник можно вписать две окружности.

Тогда, центры этих окружностей равноудалены от вершин треугольника.

Но такая точка только одна – это точка пересечения серединных перпендикуляров.

Следствие

Если все серединные перпендикуляры к сторонам выпуклого многоугольника пересекаются в одной точке, то около него можно описать окружность, центром которой будет точка пересечения серединных перпендикуляров.

Доказательство

Если все серединные перпендикуляры к сторонам выпуклого многоугольника пересекаются в одной точке, то эта точка равноудалена от всех его вершин, и, следовательно, окружность с центром в этой точке и с радиусом, равным расстоянию от этой точки до какой-либо из его вершин, будет описанной около этого многоугольника.

Теорема

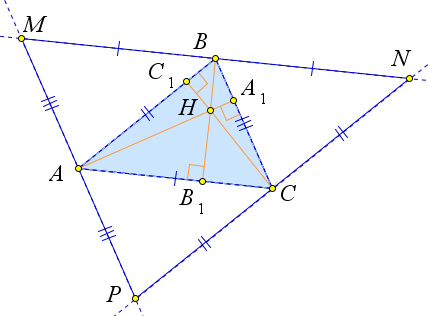
Высоты треугольника (или их продолжения) пересекаются в одной точке.

Доказательство

Докажем, что все высоты пересекаются в одной точке.

Следствие

Следствие

Серединные перпендикуляры треугольника являются высотами серединного треугольника. Следовательно, ортоцентр серединного треугольника является центром окружности, описанной около исходного треугольника.

Доказательство

Утверждение полностью следует из доказательства теоремы.

Определение

Точка пересечения высот треугольника называется ортоцентром треугольника.

Источник