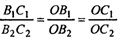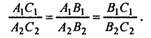докажите что через точку а

Пожалуйста решите задачу по геометрии с подробными объяснениями: как и почему! Меня завтра с ней к доске вызовут!):

Докажите, что через точку А, не лежащую в плоскости Y, проходит плоскость, параллельная плоскости Y, и притом только одна.

(рисунок надо обязательно!!)

То же самое, только вместо плоскости Y – плоскость α:

Существование плоскости, параллельной данной плоскости

Через точку вне данной плоскости можно провести плоскость, параллельную данной, и притом только одну.

Доказательство

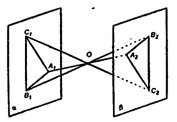
Проведем в данной плоскости α какие-нибудь две пересекающиеся прямые a и b. Через данную точку A проведем параллельные им прямые a1 и b1. Плоскость β, проходящая через прямые a1 и b1, по теореме о признаке параллельности плоскостей параллельна плоскости α.

Предположим, что через точку A проходит другая плоскость β1, тоже параллельная плоскости α. Отметим на плоскости β1 какую-нибудь точку С, не лежащую в плоскости β. Проведем плоскость γ через точки A, С и какую-нибудь точку B плоскости α. Эта плоскость пересечет плоскости α, β и β1 по прямым b, a и с. Прямые a и с не пересекают прямую b, так как не пересекают плоскость α. Следовательно, они параллельны прямой b. Но в плоскости γ через точку A может проходить только одна прямая, параллельная прямой b. что противоречит предположению. Теорема доказана.

Источник

Докажите, что треугольники подобны. Вопросы и задачи 64, Геометрия, 10-11 класс, Атанасян Л.С.

Привет. Запуталась при решении, нужна помощь знатоков.

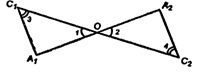
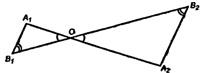
Три прямые, проходящие через одну точку и не лежащие в одной плоскости, пересекают одну из параллельных плоскостей в точках А₁, В₁ и С₁ а другую — в точках А₂, В₂ и С₂. Докажите, что треугольники А₁В₁С₁ и А₂В₂С₂ подобны.

Привет, лови свою задачку!

Две пересекающиеся прямые единственным образом задают плоскость.
Прямые А₁А₂ и В₁В₂ пересекаются и задают плоскость А₁В₁В₂. По свойству параллельных плоскостей (п. 11, 1°), А₁В₁ || A₂В₂.
Аналогично: А₁С₁ || А₂С₂; В₁С₁ || В₂С₂; ΔОА₁С₁

ΔОА₂С₂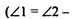

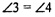
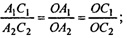
как вертикальные, как накрест лежащие);
ΔОА₁В₁

ΔOA₂B₂;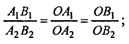

ΔОВ₁С₁

ΔОВ₂С₂;
Учитывая полученные соотношения, получим

Значит, ΔA₁B₁C₁

ΔА₂В₂С₂ по третьему признаку подобия (про- порциональность сторон).

Источник