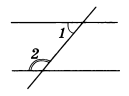
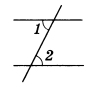
докажите что если накрест лежащие углы равны то прямые параллельны

Геометрия. 7 класс

Конспект урока

Признаки параллельности прямых

Перечень рассматриваемых вопросов:

Две прямые на плоскости называются параллельными, если они не пересекаются.

Признаки параллельности двух прямых:

1. Если при пересечении двух прямых секущей, накрест лежащие углы равны, то прямые параллельны.

2. Если при пересечении двух прямых секущей, соответственные углы равны, то прямые параллельны.

3. Если при пересечении двух прямых секущей, сумма односторонних углов равна 180°, то прямые параллельны.

Теоретический материал для самостоятельного изучения.

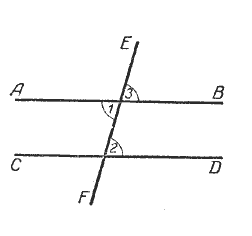
Вы уже знаете, что при пересечении двух прямых секущей образуются углы:

Прямая c называется секущей по отношению к прямым a и b, если она пересекает их в двух точках.

Рассмотрим и докажем признаки параллельности прямых.

Если при пересечении двух прямых секущей, накрест лежащие углы равны, то прямые параллельны.

Дано: прямые a и b, секущая AB, ∠ 1 = ∠ 2 накрест лежащие.

В этом случае две прямые, перпендикулярные к третьей не пересекаются, т. е. параллельны.

2 случай: ∠ 1= ∠ 2 ≠ 90°

1) Из середины O отрезка AB проведём перпендикуляр OH к прямой а. На прямой b от точки B отложим отрезок BH₁, равный отрезку AH и проведем отрезок OH₁.

2) AO = OB т. к. O середина AB; AH = BH₁ по построению; ∠1 = ∠2 по условию. Тогда ΔOHA = ΔOH₁B по первому признаку равенства треугольников.

Далее следует из равенства треугольников: ∠3 = ∠4 и ∠5 = ∠6.

3) Из равенства углов ∠3 и ∠4 следует, что точка H₁ лежит на продолжении луча OH. Это значит, что точки H₁, O, H лежат на одной прямой.

4) Из равенства ∠5 и ∠6 следует, что ∠6 = 90°. Это значит, что прямые a и b перпендикулярны к третьей НН₁, а значит, по теореме о двух прямых, перпендикулярных к третьей, не пересекаются, т. е. параллельны.

Если при пересечении двух прямых секущей, соответственные углы равны, то прямые параллельны.

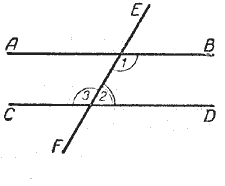
Дано: прямые a и b, секущая AB, ∠1 = ∠2 соответственные.

∠1 = ∠2 – по условию и ∠2 = ∠3 – по свойству вертикальных углов.

Значит, ∠1 = ∠3, это накрест лежащие углы, следовательно, a║b по теореме 1.

Если при пересечении двух прямых секущей, сумма односторонних углов равна 180°, то прямые параллельны.

Прямые a и b, секущая AB, ∠1 + ∠2 = 180° ‑ односторонние.

∠3 +∠2 = 180°– по свойству смежных углов, откуда ∠3 = 180° – ∠2.

∠1 + ∠2 = 180 ° по условию, откуда ∠1 = 180° – ∠2.

Тогда ∠1 = ∠3, это накрест лежащие углы, следовательно, a║b по теореме 1.

Разбор заданий тренировочного модуля.

Ответ: прямые a и b параллельны по 1 признаку параллельности прямых.

Дано: ΔABC – равнобедренный, ∠А = 60°. CD – биссектриса ∠BCK.

Ответ: AB║CD по 2 признаку параллельности прямых.

Источник

Прямая линия. Признаки параллельности прямых линий.

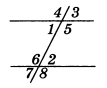
Если две произвольные прямые AB и СD пересечены третьей прямой MN, то образовавшиеся при этом углы получают попарно такие названия:

соответственные углы: 1 и 5, 4 и 8, 2 и 6, 3 и 7;

внутренние накрест лежащие углы: 3 и 5, 4 и 6;

внешние накрест лежащие углы: 1 и 7, 2 и 8;

внутренние односторонние углы: 3 и 6, 4 и 5;

внешние односторонние углы: 1 и 8, 2 и 7.

Описанные углы видны на рисунке:

Теорема.

Если две параллельные прямые пересечены третьей прямой, то сформировавшиеся:

1. внутренние накрест лежащие углы одинаковы;

2. внешние накрест лежащие углы одинаковы;

3. соответственные углы одинаковы;

4. сумма внутренних односторонних углов будет 2d = 180 0 ;

5. сумма внешних односторонних углов будет 2d = 180 0 ;

Данную теорему иллюстрирует рисунок:

Имеются две параллельные прямые AB и СD, их пересекает третья прямая MN.

3. ∠ 2 =∠ 6, ∠ 1 = ∠ 5, ∠ 3 = ∠ 7, ∠ 4 = ∠ 8;

4. ∠ 3 + ∠ 6 = 2d и ∠ 4 + ∠ 5 = 2d;

5. ∠ 2 + ∠ 7 = 2d и ∠ 1 + ∠ 8 = 2d.

2. Внешние накрест лежащие углы равны соответственно внутренним накрест лежащим углам, как углы вертикальные.

Так, ∠ 2 = ∠ 4 и ∠ 8 = ∠ 6, но по доказанному ∠ 4 = ∠ 6.

Следовательно, ∠ 2 =∠ 8.

3. Соответственные углы 2 и 6 одинаковы, поскольку ∠ 2 = ∠ 4, а ∠ 4 = ∠ 6. Также убедимся в равенстве других соответственных углов.

5. Сумма внешних односторонних углов будет 2d, потому что эти углы равны соответственно внутренним односторонним углам, как углы вертикальные.

Из выше доказанного обоснования получаем обратные теоремы.

Когда при пересечении двух прямых произвольной третьей прямой получим, что:

1. Внутренние накрест лежащие углы одинаковы;

или 2. Внешние накрест лежащие углы одинаковые;

или 3. Соответственные углы одинаковые;

или 4. Сумма внутренних односторонних углов равна 2d = 180 0 ;

или 5. Сумма внешних односторонних равна 2d = 180 0 ,

Источник

Геометрия. 7 класс

Конспект урока

Признаки параллельности прямых

Перечень рассматриваемых вопросов:

Две прямые на плоскости называются параллельными, если они не пересекаются.

Признаки параллельности двух прямых:

1. Если при пересечении двух прямых секущей, накрест лежащие углы равны, то прямые параллельны.

2. Если при пересечении двух прямых секущей, соответственные углы равны, то прямые параллельны.

3. Если при пересечении двух прямых секущей, сумма односторонних углов равна 180°, то прямые параллельны.

Теоретический материал для самостоятельного изучения.

Вы уже знаете, что при пересечении двух прямых секущей образуются углы:

Прямая c называется секущей по отношению к прямым a и b, если она пересекает их в двух точках.

Рассмотрим и докажем признаки параллельности прямых.

Если при пересечении двух прямых секущей, накрест лежащие углы равны, то прямые параллельны.

Дано: прямые a и b, секущая AB, ∠ 1 = ∠ 2 накрест лежащие.

В этом случае две прямые, перпендикулярные к третьей не пересекаются, т. е. параллельны.

2 случай: ∠ 1= ∠ 2 ≠ 90°

1) Из середины O отрезка AB проведём перпендикуляр OH к прямой а. На прямой b от точки B отложим отрезок BH₁, равный отрезку AH и проведем отрезок OH₁.

2) AO = OB т. к. O середина AB; AH = BH₁ по построению; ∠1 = ∠2 по условию. Тогда ΔOHA = ΔOH₁B по первому признаку равенства треугольников.

Далее следует из равенства треугольников: ∠3 = ∠4 и ∠5 = ∠6.

3) Из равенства углов ∠3 и ∠4 следует, что точка H₁ лежит на продолжении луча OH. Это значит, что точки H₁, O, H лежат на одной прямой.

4) Из равенства ∠5 и ∠6 следует, что ∠6 = 90°. Это значит, что прямые a и b перпендикулярны к третьей НН₁, а значит, по теореме о двух прямых, перпендикулярных к третьей, не пересекаются, т. е. параллельны.

Если при пересечении двух прямых секущей, соответственные углы равны, то прямые параллельны.

Дано: прямые a и b, секущая AB, ∠1 = ∠2 соответственные.

∠1 = ∠2 – по условию и ∠2 = ∠3 – по свойству вертикальных углов.

Значит, ∠1 = ∠3, это накрест лежащие углы, следовательно, a║b по теореме 1.

Если при пересечении двух прямых секущей, сумма односторонних углов равна 180°, то прямые параллельны.

Прямые a и b, секущая AB, ∠1 + ∠2 = 180° ‑ односторонние.

∠3 +∠2 = 180°– по свойству смежных углов, откуда ∠3 = 180° – ∠2.

∠1 + ∠2 = 180 ° по условию, откуда ∠1 = 180° – ∠2.

Тогда ∠1 = ∠3, это накрест лежащие углы, следовательно, a║b по теореме 1.

Разбор заданий тренировочного модуля.

Ответ: прямые a и b параллельны по 1 признаку параллельности прямых.

Дано: ΔABC – равнобедренный, ∠А = 60°. CD – биссектриса ∠BCK.

Ответ: AB║CD по 2 признаку параллельности прямых.

Источник

Инструменты пользователя

Инструменты сайта

Боковая панель

Геометрия:

Контакты

Признаки параллельности двух прямых. Свойства параллельных прямых

Признаки параллельности двух прямых

Теорема 1. Если при пересечении двух прямых секущей:

прямые параллельны (рис.1).

Доказательство. Ограничимся доказательством случая 1.

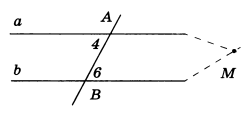
Пусть при пересечении прямых а и b секущей АВ накрест лежащие углы равны. Например, ∠ 4 = ∠ 6. Докажем, что а || b.

Предположим, что прямые а и b не параллельны. Тогда они пересекаются в некоторой точке М и, следовательно, один из углов 4 или 6 будет внешним углом треугольника АВМ. Пусть для определенности ∠ 4 — внешний угол треугольника АВМ, а ∠ 6 — внутренний. Из теоремы о внешнем угле треугольника следует, что ∠ 4 больше ∠ 6, а это противоречит условию, значит, прямые а и 6 не могут пересекаться, поэтому они параллельны.

Замечание. Способ, которым мы только что доказали случай 1 теоремы 1, называется методом доказательства от противного или приведением к нелепости. Первое название этот способ получил потому, что в начале рассуждения делается предположение, противное (противоположное) тому, что требуется доказать. Приведением к нелепости он называется вследствие того, что, рассуждая на основании сделанного предположения, мы приходим к нелепому выводу (к абсурду). Получение такого вывода заставляет нас отвергнуть сделанное вначале допущение и принять то, которое требовалось доказать.

Задача 1. Построить прямую, проходящую через данную точку М и параллельную данной прямой а, не проходящей через точку М.

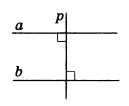
Решение. Проводим через точку М прямую р перпендикулярно прямой а (рис. 3).

Затем проводим через точку М прямую b перпендикулярно прямой р. Прямая b параллельна прямой а согласно следствию из теоремы 1.

Из рассмотренной задачи следует важный вывод:
через точку, не лежащую на данной прямой, всегда можно провести прямую, параллельную данной.

Основное свойство параллельных прямых состоит в следующем.

Аксиома параллельных прямых. Через данную точку, не лежащую на данной прямой, проходит только одна прямая, параллельная данной.

Рассмотрим некоторые свойства параллельных прямых, которые следуют из этой аксиомы.

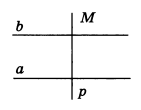
1) Если прямая пересекает одну из двух параллельных прямых, то она пересекает и другую (рис.4).

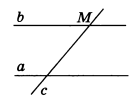
2) Если две различные прямые параллельны третьей прямой, то они параллельны (рис.5).

Справедлива и следующая теорема.

Теорема 2. Если две параллельные прямые пересечены секущей, то:

Следствие 2. Если прямая перпендикулярна к одной из двух параллельных прямых, то она перпендикулярна и к другой (см. рис.2).

Замечание. Теорема 2 называется обратной теореме 1. Заключение теоремы 1 является условием теоремы 2. А условие теоремы 1 является заключением теоремы 2. Не всякая теорема имеет обратную, т. е. если данная теорема верна, то обратная теорема может быть неверна.

Поясним это на примере теоремы о вертикальных углах. Эту теорему можно сформулировать так: если два угла вертикальные, то они равны. Обратная ей теорема была бы такой: если два угла равны, то они вертикальные. А это, конечно, неверно. Два равных угла вовсе не обязаны быть вертикальными.

Пример 1. Две параллельные прямые пересечены третьей. Известно, что разность двух внутренних односторонних углов равна 30°. Найти эти углы.

Решение. Пусть условию отвечает рисунок 6.

Углы 1 и 2 внутренние односторонние, их сумма равна 180°, т. е.
∠ l + ∠ 2 = 180°. (1)

Подставим в равенство (1) значения углов 1 и 2, получим
х + 30° + х = 180°.

Пример 2. Две параллельные прямые пересечены третьей. Известно, что сумма двух внутренних накрест лежащих углов равна 150°. Чему равны эти углы и остальные шесть?

Решение. Пусть условию задачи соответствует рисунок 7.

Углы 1 и 2 внутренние накрест лежащие, следовательно, они равны. Сумма этих углов по условию задачи равна 150°, тогда ∠ 1 = ∠ 2 = 75°.

Найдем остальные углы (рис. 8):

Получили четыре угла по 75°, четыре угла по 105°.

Источник

Признаки параллельности прямых

1. Первый признак параллельности.

Если при пересечении двух прямых третьей внутренние накрест лежащие углы равны, то эти прямые параллельны.

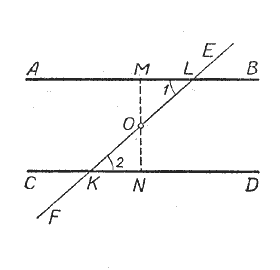
Опустим из точки О перпендикуляр ОМ на прямую АВ и продолжим его до пересечения с прямой СD, АВ ⊥ МN. Докажем, что и СD ⊥ МN.

∠МОL = ∠NОК, как вертикальные углы. Таким образом, сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника; следовательно, ΔМОL = ΔNОК, а отсюда и ∠LМО = ∠КNО,
но ∠LМО прямой, значит, и ∠КNО тоже прямой. Таким образом, прямые АВ и СD перпендикулярны к одной и той же прямой МN, следовательно, они параллельны, что и требовалось доказать.

Примечание. Пересечение прямых МО и СD может быть установлено путём поворота треугольника МОL вокруг точки О на 180°.

2. Второй признак параллельности.

Посмотрим, будут ли параллельны прямые АВ и СD, если при пересечении их третьей прямой ЕF равны соответственные углы.

Пусть какие-нибудь соответственные углы равны, например ∠ 3 = ∠2 (рис.);

Если при пересечении двух прямых третьей соответственные углы равны, то эти две прямые параллельны.

На этом свойстве основано построение параллельных прямых при помощи линейки и чертёжного треугольника. Выполняется это следующим образом.

Приложим треугольник к линейке так, как это показано на рис. Будем передвигать треугольник так, чтобы одна его сторона скользила по линейке, а по какой-либо другой стороне треугольника проведём несколько прямых. Эти прямые будут параллельны.

3. Третий признак параллельности.

Пусть нам известно, что при пересечении двух прямых АВ и СD третьей прямой сумма каких-нибудь внутренних односторонних углов равна 2d (или 180°). Будут ли в этом случае прямые АВ и СD параллельны (рис.).

Пусть ∠1 и ∠2-внутренние односторонние углы и в сумме составляют 2d.

Но ∠3 + ∠2 = 2d, как углы смежные. Следовательно, ∠1 + ∠2 = ∠3+ ∠2.

Отсюда ∠1 = ∠3, а эти углы внутренние накрест лежащие. Следовательно, АВ || СD.

Если при пересечении двух прямых третьей сумма внутренних односторонних углов равна 2d (или 180°), то эти две прямые параллельны.

Признаки параллельных прямых:

1. Если при пересечении двух прямых третьей внутренние накрест лежащие углы равны, то эти прямые параллельны.

2.Если при пересечении двух прямых третьей соответственные углы равны, то эти две прямые параллельны.

3. Если при пересечении двух прямых третьей сумма внутренних односторонних углов равна 180°, то эти две прямые параллельны.

4. Если две прямые параллельны третьей прямой, то они параллельны между собой.

5. Если две прямые перпендикулярны третьей прямой, то они параллельны между собой.

Аксиома параллельности Евклида

Задача. Через точку М, взятую вне прямой АВ, провести прямую, параллельную прямой АВ.

Пользуясь доказанными теоремами о признаках параллельности прямых, можно эту задачу решить различными способами,

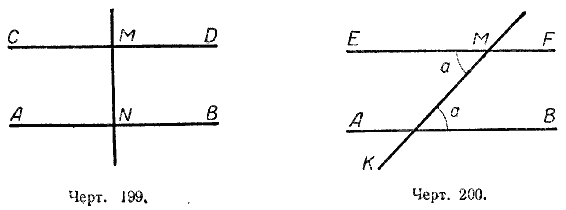
Решение. 1-й с п о с о б (черт. 199).

Проводим МN⊥АВ и через точку М проводим СD⊥МN;

получаем СD⊥МN и АВ⊥МN.

На основании теоремы («Если две прямые перпендикулярны к одной и той же прямой, то они параллельны.») заключаем, что СD || АВ.

2-й с п о с о б (черт. 200).

Проводим МК, пересекающую АВ под любым углом α, и через точку М проводим прямую ЕF, образующую с прямой МК угол ЕМК, равный углу α. На основании теоремы (Признаки параллельности прямых) заключаем, что ЕF || АВ.

Решив данную задачу, можем считать доказанным, что через любую точку М, взятую вне прямой АВ, можно провести прямую, ей параллельную. Возникает вопрос, сколько же прямых, параллельных данной прямой и проходящих через данную точку, может существовать?

Практика построений позволяет предполагать, что существует только одна такая прямая, так как при тщательно выполненном чертеже прямые, проведённые различными способами через одну и ту же точку параллельно одной и той же прямой, сливаются.

В теории ответ на поставленный вопрос даёт так называемая аксиома параллельности Евклида; она формулируется так:

Через точку, взятую вне дaнной прямой, можно провести только одну прямую, параллельную этой прямой.

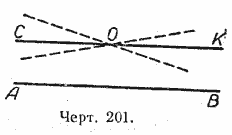
На чертеже 201 через точку О проведена прямая СК, параллельная прямой АВ.

Всякая другая прямая, проходящая через точку О, уже не будет параллельна прямой АВ, а будет её пересекать.

Принятая Евклидом в его «Началах» аксиома, которая утверждает, что на плоскости через точку, взятую вне данной прямой, можно провести только одну прямую, параллельную этой прямой, называется аксиомой параллельности Евклида.

Более двух тысячелетий после Евклида многие учёные-математики пытались доказать это математическое предложение, но всегда их попытки оказывались безуспешными. Только в 1826 г. великий русский учёный, профессор Казанского университета Николай Иванович Лобачевский доказал, что, используя все другие аксиомы Евклида, это математическое предложение доказать нельзя, что оно действительно должно быть принято за аксиому. Н. И. Лобачевский создал новую геометрию, которая в отличие от геометрии Евклида названа геометрией Лобачевского.

Источник