докажите что если в треугольнике биссектриса является медианой
Медиана треугольника является его биссектрисой
Выясним, какой вывод следует из того, что медиана треугольника является его биссектрисой?
Если медиана треугольника является его биссектрисой, то этот треугольник — равнобедренный.

CK — медиана и биссектриса
Проведем анализ задачи.
На основе каких данных можно утверждать, что треугольник — равнобедренный? Если у него две стороны равны либо два угла равны. Значит, нам нужно доказать либо равенство сторон AC и BC, либо равенство углов A и B. Любое из этих равенств следует из равенства треугольников.
В треугольниках AKC и BKC биссектриса CK образует равные углы ACK и BCK, медиана CK — равные отрезки AK и BK. Сторона CK — общая.
Что мы имеем? Две стороны, но нет угла между ними. Ни к одной из сторон нет двух прилежащих углов. Признаки равенства треугольников применить не можем.
В таком случае придется выполнять дополнительные построения.
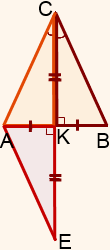
Мы можем доказать, что этот треугольник равен треугольнику BKC (по двум сторонам и углу между ними).
Из равенства этих треугольников следует равенство сторон AE и BC и углов AEK и BCK.
Получается, что в треугольнике ACE имеется два равных угла AEK и ACK. Поэтому он — равнобедренный, откуда легко доказывается и равенство сторон AC и ВС. Осталось записать доказательство.
На луче CK отложим отрезок KE, KE=CK.
Рассмотрим треугольники AKE и BKC:
1) AK=BK (так как CK — медиана по условию)
2) KE=CK (по построению)
3) ∠AKE=∠BKC (как вертикальные).
Следовательно, ∆ AKE=∆ BKC (по двум сторонам и углу между ними).
Из равенства треугольников следует равенство соответствующих сторон: AE=BC и соответствующих углов: ∠AEK=∠BCK.
По условию, ∠BCK=∠AСK. Поэтому ∠AEK=∠AСK.
Таким образом получили, что в треугольнике ACE два угла равны. Значит, ∆ ACE — равнобедренный с основанием CE (по признаку). Следовательно, его боковые стороны равны: AE=AC.
А поскольку уже доказали, что AE=BC, то и AС=BС. Поэтому ∆ ABC — равнобедренный с основанием AB (по определению).
Что и требовалось доказать.
Если в треугольнике совпадают медиана и биссектриса, проведенные к каждой из сторон, то такой треугольник — равносторонний (каждые две его стороны равны между собой, значит, равны все три стороны).
Треугольник. Важные факты о высоте, биссектрисе и медиане
Определения
Медиана треугольника – это отрезок, соединяющий вершину треугольника с серединой противоположной стороны.
Биссектриса треугольника – это отрезок биссектрисы угла треугольника, соединяющий вершину треугольника с точкой противоположной стороны.
Высота треугольника – это перпендикуляр, проведенный из вершины треугольника к прямой, содержащей противоположную сторону.
Теорема
В любом треугольнике высоты (или их продолжения) пересекаются в одной точке (рис. 1 и 2), биссектрисы пересекаются в одной точке (рис. 3), медианы пересекаются в одной точке (рис. 4).
Теорема
В равнобедренном треугольнике биссектриса, проведённая к основанию, является медианой и высотой.
Верны и другие утверждения:
В равнобедренном треугольнике высота, проведенная к основанию, является биссектрисой и медианой.
В равнобедренном треугольнике медиана, проведенная к основанию, является биссектрисой и высотой.
Теорема
Доказательство
Для других медиан треугольника \(ABC\) требуемое свойство доказывается аналогично.
Теорема
Медиана треугольника делит его на два равновеликих треугольника (равновеликие треугольники – это треугольники, у которых площади равны).
Доказательство
Теорема
В прямоугольном треугольнике медиана, проведенная к гипотенузе, равна половине гипотенузы.
Верно и обратное: если медиана равна половине стороны, к которой она проведена, то она проведена из вершины прямого угла.
Доказательство
Теорема
Биссектриса треугольника делит его сторону на части, пропорциональные прилежащим сторонам:
Верно и обратное: если отрезок, проведенный из вершины треугольника к стороне, делит эту сторону на отрезки, пропорциональные прилежащим сторонам, то это биссектриса.
Доказательство
Площади треугольников, у которых есть равные углы, относятся как произведения сторон, образующих эти углы, то есть \[\dfrac
Теорема
Если точка равноудалена от сторон угла, то она лежит на его биссектрисе.
Верно и обратное: если точка лежит на биссектрисе угла, то она равноудалена от его сторон.
Доказательство
Геометрия. 7 класс
Конспект урока
Перечень рассматриваемых вопросов:
Биссектриса угла треугольника – это отрезок биссектрисы угла треугольника, соединяющий вершину треугольника с точкой противоположной стороны.
Медиана треугольника – это отрезок, соединяющий вершину треугольника с серединой противоположной стороны.
Высота треугольника – это перпендикуляр, проведённый из вершины треугольника к прямой, содержащей противоположную сторону.
Равнобедренный треугольник – треугольник, у которого две стороны равны.
Равносторонний треугольник – треугольник, у которого все стороны равны.
Любой равносторонний треугольник является равнобедренным, обратное не верно.
Теоретический материал для самостоятельного изучения.
Вы уже познакомились с такими понятиями как треугольник, рассмотрели его виды.
Рассмотрим такие виды треугольников: как равнобедренные и равносторонние, более подробно. Начнём с описания равнобедренного треугольника. Но для начала, дадим ему определение.
Треугольник называется равнобедренным, если две его стороны равны.
В равнобедренном треугольнике равные стороны называются боковыми, а третья сторона – основанием.
AB и BC – боковые стороны ∆ABC.
Если третья сторона равна двум другим, то любая сторона может быть основанием.
Теперь рассмотрим треугольник, у которого все стороны равны. Такой треугольник называется равносторонним.
Докажем две теоремы о свойствах равнобедренного треугольника.
Теорема: В равнобедренном треугольнике углы при основании равны.
Теперь сформулируем теорему о биссектрисе, медиане и высоте равнобедренного треугольника, проведённых к основанию.
В равнобедренном треугольнике биссектриса, проведённая к основанию, является медианой и высотой треугольника.
AF– биссектриса ΔABC
Доказать: AF – медиана и высота.
Справедливы и следующие утверждения.
Высота равнобедренного треугольника, проведённая к основанию, является медианой и биссектрисой.
А медиана равнобедренного треугольника, проведённая к основанию, является высотой и биссектрисой.
AF – медиана ∠ВАС ΔABC
Доказать: AF – биссектриса и высота ΔABC.
∆ABF = ∆ACF т. к. ∠В = ∠С (по свойству равнобедренного треугольника); BF = CF (по определению медианы треугольника); AB = AC (∆ABC – по определению равнобедренного треугольника) → ∠BАF = ∠FАC (как соответствующие элементы равных треугольников) => AF ‑ биссектриса ΔABC (по определению биссектрисы треугольника).
∠AFB = ∠AFC как соответствующие элементы равных треугольников, но их сумма равна 180 (по свойству развернутого угла).
∠AFB = ∠AFC = 90° →AF – высота треугольника (по определению высоты треугольника).
Сегодня мы узнали, что такое равнобедренный, равносторонний треугольник, рассмотрели свойства равнобедренного треугольника.
Разберем задачу на доказательство.
Рассмотрим, как можно решить задачу на доказательство, используя понятие: «медиана равнобедренного треугольника».
На рисунке изображён треугольник ABC, при этом AM – медиана, при этом AM = BM. Докажем, что угол А равен сумме двух других углов ∆ABC.
По условию AМ = ВМ → ∆АВМ – равнобедренный (по определению равнобедренного треугольника)→ ∠МВА = ∠ВАМ (по свойству равнобедренного треугольника).
Т. к. АМ – медиана ∆ABC и AМ = ВМ → AМ = ВМ = СМ → ∆АМС – равнобедренный (по определению равнобедренного треугольника) → ∠МСА = ∠ВАС (по свойству равнобедренного треугольника).
Получаем, что ∠А = ∠ВАС + ∠ВАМ = ∠МВА + ∠МСА = ∠В + ∠С.
Что и требовалось доказать.
Разбор решения заданий тренировочного модуля.
Периметр равнобедренного треугольника ABC равен 50 см, боковая сторона AC на 4 см больше основания BC. Найдите основание треугольника.
Решение: Пусть х – основание ВС треугольника АВС, тогда АС = АВ (как боковые стороны равнобедренного треугольника).
АС = АВ = х + 4 (по условию).
Периметр треугольника АВС равен сумме всех его сторон, т. е. 50 см = АС + ВС + АВ,
х = 14 см – основание BC.
На рисунке изображён равнобедренный треугольник ABC. AC – основание треугольника, ∠1 = 120. Найдите ∠2.
Решение: ∠1 и ∠АСВ – смежные →∠1 + ∠АСВ = 180, значит:
АВС – равнобедренный, значит: ∠ВАС = ∠АСВ = 60 (углы при основании равнобедренного треугольника равны).














