докажите что геометрическое место точек
Геометрическое место точек
Геометрическое место точек (ГМТ) — это фигура, состоящая из всех точек плоскости, удовлетворяющих определённому условию.
Чтобы выяснить, что собой представляет некоторая фигура F — геометрическое место точек, удовлетворяющих заданному условию P, нужно доказать:
1) если определённая точка принадлежит фигуре F, то она удовлетворяет заданному условию P;
2) если определённая точка удовлетворяет заданному условию P, то она принадлежит фигуре F.
(то есть требуется доказать прямую теорему — свойство P точек, принадлежащих фигуре F, и обратную теорему — признак фигуры F: если точка удовлетворяет условию P, то она принадлежит F).
Геометрическое место точек, равноудалённых от данной точки — окружность.
Это следует непосредственно из определения окружности.
Некоторые теоремы о ГМТ
1) Геометрическим местом точек, равноудалённых от двух данных точек, является серединный перпендикуляр к отрезку, соединяющему эти точки.
2) Геометрическим местом точек, равноудалённых от сторон неразвёрнутого угла, является биссектриса этого угла.
3) Геометрическим местом точек, удалённых от данной прямой на расстояние h, состоит из двух прямых, параллельных данной прямой и отстоящих от неё на h.
4) Геометрическим местом точек, равноудалённых от двух параллельных прямых, является прямая, параллельная этим прямым и проходящая через середину их общего перпендикуляра.
Понятие ГМТ часто используют при решении задач на построение.
Геометрическое место точек. Теорема о геометрическом месте точек, равноудалённых от двух данных точек, в геометрической и аналитической формах



Определение. Геометрическое место точек – фигура, которая состоит из всех точек на плоскости, обладающих определённым свойством.
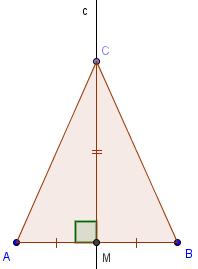
Теорема. Геометрическое место точек, равноудалённых от двух данных точек, есть серединный перпендикуляр к отрезку, соединяющему эти точки, то есть прямая, перпендикулярная этому отрезку и проходящая через его середину.
1)
Пусть точка C равноудалена от A и B. Отметим точку M – середину отрезка AB. Треугольники ACM и BCM равны по трём сторонам. Углы AMC и BMC равны и дают в сумме развёрнутый угол. Значит, они оба равны 90°.
Мы доказали, что все точки, равноудалённые от двух данных точек, лежат на серединном перпендикуляре.
2) Пусть точка C лежит на серединном перпендикуляре к AB. Треугольники AMC и BMC равны двум катетам, значит, AC=BC.
Мы доказали, что все точки серединного перпендикуляра к отрезку равноудалены от его концов.
Таким образом, геометрическое место точек, равноудалённых от двух данных точек, и серединный перпендикуляр к отрезку, соединяющему эти точки, совпадают.
Планиметрия. Страница 3
| Главная > Учебные материалы > Математика: Планиметрия. Страница 3 | ||||
 | ||||
 |  Рис.3 Теорема. Окружность, вписанная в треугольник. 4.Геометрическое место точекГеометрическое место точек это фигура, которая представляет собой совокупность точек на плоскости, подчиняющихся определенному закону или обладающих определенным свойством. Теорема. Геометрическим местом точек называется прямая, все точки которой равноудалены от двух данных точек, перпендикулярная отрезку, соединяющему эти точки и проходящая через его середину. Доказательство. Пусть дан отрезок АС. Прямая А проходит через середину этого отрезка и перпендикулярна ему.(Рис. 4). Тогда треугольники Δ АМВ и Δ СМВ равны. Так как сторона ВМ у них обшая, а стороны АМ и МС равны по условию. Следовательно точка В равноудалена от точек А и С. |  Рис.4 Теорема. Геометрическое место точек. | ||
 | ||||
 | ||||
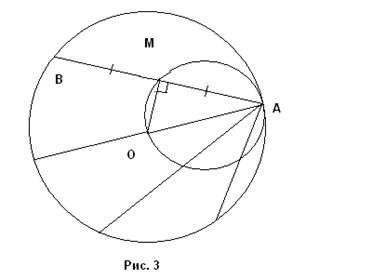
 Рис.5 Задача. Дана окружность с центром О. Пример 2Докажите, что касательная к окружности не имеет с ней других общих точек, кроме точки касания. (Рис.6) Доказательство: Таким образом, в равнобедренном треугольнике АОВ углы при вершинах А и В равны 90°. А это невозможно. Следовательно, мы пришли к противоречию и прямая а не может касаться окружности в двух точках. Рис.6 Задача. Касательная к окружности. Пример 3Точки А,В,С лежат на одной прямой, а точка О лежит вне этой прямой. Докажите, что треугольники АОВ и ВОС не могут быть равнобедренными с основаниями АВ и ВС. (Рис.7) Доказательство: Допустим, что треугольники АОВ и ВОС равнобедренные с основаниями АВ и ВС. Тогда Стороны АО, ВО и СО равны. Отсюда следует, что углы ОАВ, АВО, ОВС и ОСВ равны. И ∠АВО = ∠ОВС = 90°, так как эти углы являются смежными, а их сумма равна 180°. Таким образом, в равнобедренных треугольниках АОВ и ВОС углы при вершинах А и С равны 90°. А это невозможно, потому, что тогда стороны АО, ВО и СО были бы параллельны, так как они перпендикулярны одной прямой АС. Следовательно, мы пришли к противоречию, и треугольники АОВ и ВОС не могут быть равнобедренными с основаниями АВ и ВС. Рис.7 Задача. Даны три точки на прямой. Пример 4Окружности с центрами О и О1 пересекаются в точках А и В. Докажите, что прямая АВ перпендикулярна прямой ОО1 (Рис.8) Доказательство: Так как окружности пересекаются в точках А и В, то эти две точки принадлежат обеим окружностям. Следовательно, отрезок ОА = ОВ, как радиусы окружности с центром в точке О. А отрезок О1А = О1В, как радиусы окружности с центром в точке О1. Таким образом, треугольники ОАО1 и ОВО1 равны по третьему признаку равенства треугольников (по трем сторонам). А следовательно отрезки АС и ВС равны. И прямая ОО1 является геометрическим местом точек для двух данных точек А и В. Т.е. любая точка прямой ОО1 равноудалена от двух данных точек А и В. Следовательно, треугольники ОАС и ОВС равны, также как и треугольники АСО1 и ВСО1 по трем сторонам. А отсюда следует равенство углов при вершине С. Т.е. ∠ОСА = ∠ОСВ = ∠АСО1 = ∠ВСО1 = 90°. Следовательно, можно сделать вывод, что прямая АВ перпендикулярна прямой ОО1. Рис.8 Задача. Окружности с центрами О и О1. Пример 5Отрезок ВС пересекает прямую а в точке О. Расстояние от точек В и С до прямой а равны. Докажите, что точка О является серединой отрезка ВС (Рис.9) Доказательство: По условию задачи, расстояния от точек В и С до прямой а равны. Т.е. РС = BQ. Так как расстояние от точки до прямой представляет собой перпендикуляр, то два треугольника РОС и ВОQ, образованные двумя пересекающимися прямыми ВС и а, и перпендикулярами, опущенными на одну из них, равны по второму признаку равенства треугольников ( по стороне и двум прилегающим к ней углам: РС = BQ, углы при вершинах В и С равны как внутренние накрест лежащие, а углы при вершинах Р и Q прямые). Из равенства треугольников РОС и ВОQ следует, что ВО = ОС. Геометрические места точек
Определение.Геометрическим местом точек (в дальнейшем ГМТ), называется фигура плоскости, состоящая из точек обладающих некоторым свойством, и не содержащая ни одной точки, не обладающей этим свойством. Мы будем рассматривать только те ГМТ, которые можно построить с помощью циркуля и линейки. Рассмотрим ГМТ на плоскости, обладающие простейшими и наиболее часто выражающимися свойствами: 1) ГМТ, отстоящих на данном расстоянии r от данной точки О, есть окружность с центром в точке О радиуса r. 2) ГМТ равноудаленных от двух данных точек А и В, есть прямая, перпендикулярная к отрезку АВ и проходящая через его середину. 3) ГМТ равноудаленных от двух данных пересекающихся прямых, есть пара взаимно перпендикулярных прямых, проходящих через точку пересечения и делящих углы между данными прямыми пополам. 4) ГМТ, отстоящих на одинаковом расстоянии h от прямой, есть две прямые, параллельные этой прямой и находящиеся по разные стороны от нее на данном расстоянии h. 5) Геометрическое место центров окружностей, касающихся данной прямой m в данной на ней точке М, есть перпендикуляр к АВ в точке М (кроме точки М). 6) Геометрическое место центров окружностей, касающихся данной окружности в данной на ней очке М, есть прямая, проходящая через точку М и центр данной окружности (кроме точек М и О). 7) ГМТ, из которых данный отрезок виден под данным углом, составляет две дуги окружностей, описанных на данном отрезке и вмещающих данный угол. 8) ГМТ, расстояния от которых до двух данных точек А и В находятся в отношении m : n, есть окружность (называемая окружностью Аполлония). 9) Геометрическое место середин хорд, проведенных из одной точки окружности, есть окружность, построенная на отрезке, соединяющем данную точку с центром данной окружности, как на диаметре. 10) Геометрическое место вершин треугольников равновеликих данному и имеющих общее основание, составляет две прямые, параллельные основанию и проходящие через вершину данного треугольника и ему симметричного относительно прямой, содержащей основание. Приведем примеры отыскания ГМТ. ПРИМЕР 2. Найти ГМТ, являющихся серединами хорд, проведенных из одной точки данной окружности (ГМТ № 9). Часто метод координат позволяет находить ГМТ. ПРИМЕР 3. Найти ГМТ, расстояние от которых до двух данных точек А и В находятся в данном отношении m : n (m ≠ n). Преобразуем наше равенство. Имеем После раскрытия скобок и приведения подобных слагаемых, получаем Разделим левую и правую части последнего неравенства на
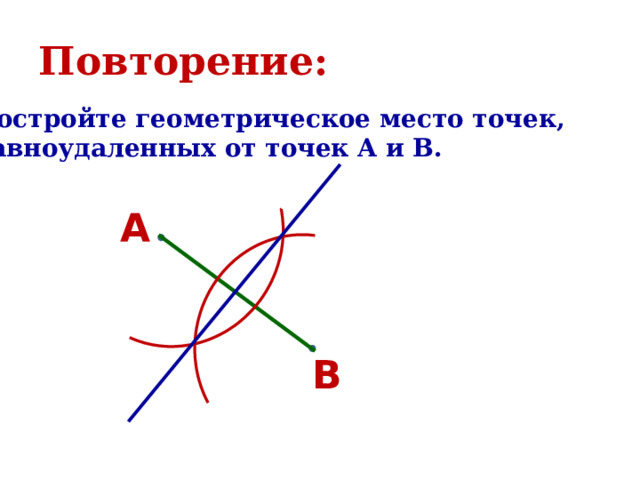
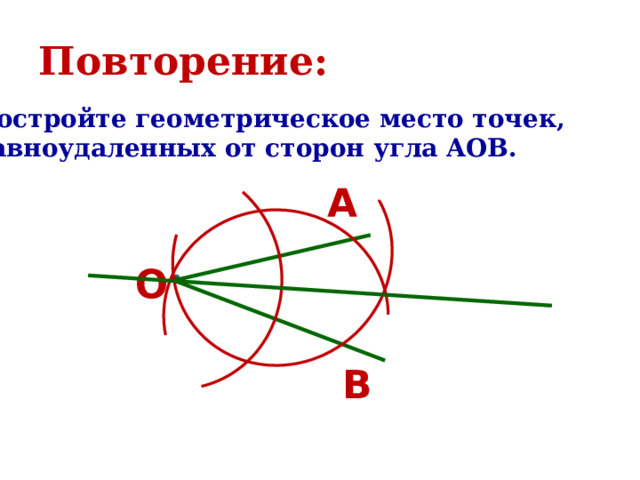
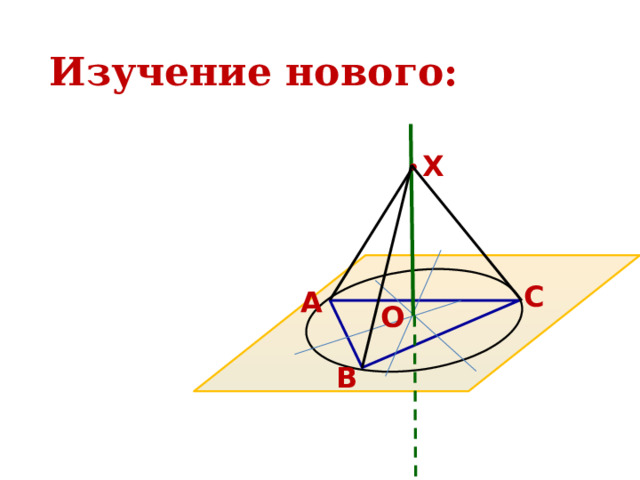
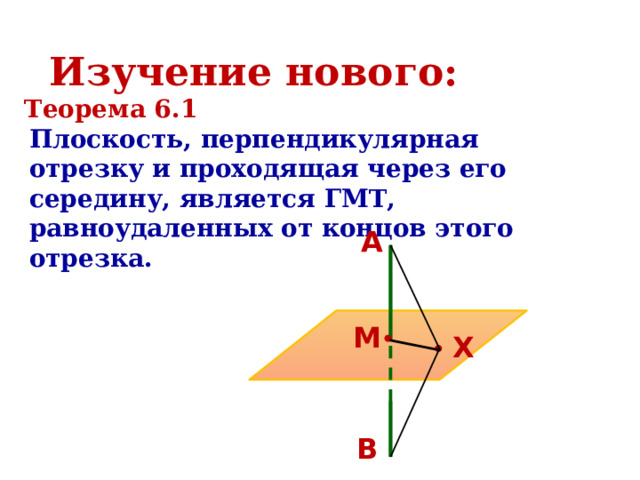
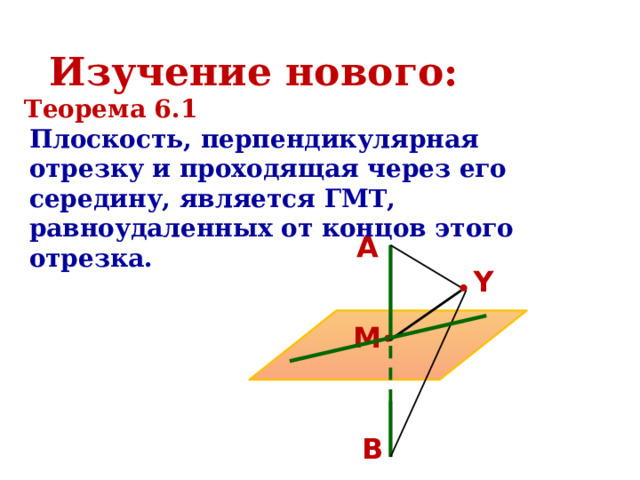
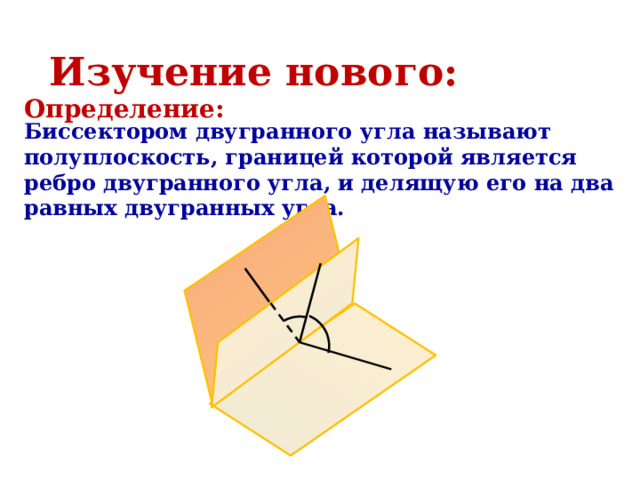
Но последнее уравнение задает окружность с центром в точке Обратно, пусть координаты точки С(x,y) удовлетворяют уравнению (**). Проделывая все выкладки в обратную сторону, приходим к равенству (*), что и доказывает принадлежность точки С нашему ГМТ. Геометрическое место точек в пространстве.Содержимое разработкиГеометрическое место точек в пространстве. Уравнение плоскости. Постройте геометрическое место точек, равноудаленных от точек A и B. Постройте геометрическое место точек, равноудаленных от сторон угла AOB. Геометрическим местом точек называется фигура, состоящая из всех точек, удовлетворяющих заданному свойству, или нескольким заданным свойствам Геометрическим местом точек (ГМТ) называют множество точек пространства, обладающих определенным свойством. Чтобы доказать, что какое-то множество точек является ГМТ, надо доказать: 1. каждая точка данного множества обладает заданным свойством; 2. если точка обладает заданным свойством, то она принадлежит данному множеству. Плоскость, перпендикулярная отрезку и проходящая через его середину, является ГМТ, равноудаленных от концов этого отрезка. Плоскость, перпендикулярная отрезку и проходящая через его середину, является ГМТ, равноудаленных от концов этого отрезка. Биссектором двугранного угла называют полуплоскость, границей которой является ребро двугранного угла, и делящую его на два равных двугранных угла. Биссектор двугранного угла является ГМТ, принадлежащих двугранному углу и равноудаленных от его граней. Уравнением фигуры F, заданной в координатном пространстве xyz, называют уравнение с тремя переменными x, y, z, обладающее следующими свойствами: Уравнение плоскости имеет вид ax + by + cz + d = 0, где a, b, c и d – некоторые числа, причем a, b, и c не равны нулю одновременно.
| ||||










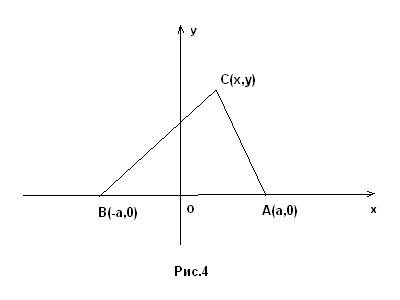
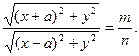 (*)
(*)
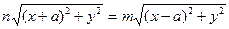
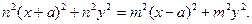
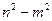 (это можно сделать, так как по условию
(это можно сделать, так как по условию 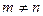 ), затем выделим полный квадрат относительно х. Получаем
), затем выделим полный квадрат относительно х. Получаем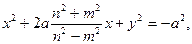
 или
или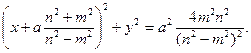 (**)
(**)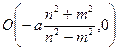 и радиусом
и радиусом 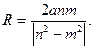 Таким образом, если точка удовлетворяет условиям задачи, то она принадлежит (**).
Таким образом, если точка удовлетворяет условиям задачи, то она принадлежит (**).