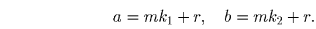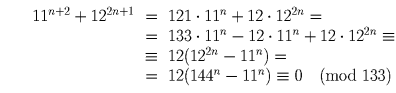докажите что n не делится на 2 в степени n
Доказать, что для любого натурального n (кроме единицы) 2^n-1 не делится на n
задан 10 Янв ’18 13:30
1 ответ
отвечен 10 Янв ’18 15:56
@Evgeny Kondr. таких сложных рассуждений тут не надо. Если m=k\nu+r, то 2^m=1 mod p и 2^\nu=1 mod p. Отсюда 2^r=2^m(2^\nu)^<-k>=1 nod p. Остаток r меньше \nu, а оно выбиралось наименьшим натуральным. Значит, r не натуральное, то есть оно равно нулю, и имеет место деление нацело.
Из Вашей формулы всё точно так же следует: 2^r-1 делится на p, и надо воспользоваться тем же условием, что \nu наименьшее. Отсюда r=0, и m=k\nu.
@falcao, так и думал( Теория графов Можно, пожалуйста, потревожить вас в последний раз перед экзаменом. Есть идеи по поводу этой задачи? Она висит на форуме давно, но человек, который дал ответ не понял условие.
@Evgeny Kondr. там есть фраза с любого острова на любой другой можно попасть не более, чем по двум мостам, которая имеет двоякое толкование. Одно такое: два острова не могут быть соединены тремя мостами. Второе: с любого острова на любой можно попасть, ПРОЕХАВ не более чем по двум мостам. Что имели в виду авторы, я не знаю. Задачи с неясным условием обычно решать не хочется.
@falcao, они же говорят, по мосту можно ехать в одну сторону, между некоторыми островами есть мосты. И еще добавляют, что либо вы попадаете из одного острова на другой напрямую или через посредника для любой пары островов. Прорешав несколько их экзаменов уже понял что они обычно хотят. Это последняя задача, по которой нет идей.
@Evgeny Kondr. я помню эту задачу, но там изначально было неправильное толкование из-за небрежной формулировки. Скорее всего, верна именно та трактовка, в которой говорилось в комментарии Романа83. Надо будет прикинуть, что получается при этом. Сейчас я пишу в перерыве между лекциями, и с мыслями собраться некогда. Позже постараюсь подумать.
Докажите что n не делится на 2 в степени n
Задача 15:
Найдите остатки от деления
а) 1989 1990 1991 + 1992³ на 7;
Решение:
Ответ: а) 0; б) 1, так как 9 дает остаток 1 при делении на 8.
Задача 16:
Докажите, что n³ + 2n делится на 3 для любого натурального n.
Решение:
Число n может давать при делении на 3 один из трех остатков: 0, 1, 2. Рассмотрим три случая.
Если n дает остаток 0, то и n³ и 2n делятся на 3 и поэтому n³ + 2n также делится на 3.
Если n дает остаток 1, то n³ дает остаток 1, 2n – остаток 2, а 1 + 2 делится на 3.
Если n дает остаток 2, то n² дает остаток 1, n³ – остаток 2, 2n – остаток 1, а 2 + 1 делится на 3.
Задача 17:
Докажите, что n 5 + 4n делится на 5 при любом натуральном n.
Решение:
Указание: Переберите остатки от деления на 5.
Задача 18:
Докажите, что n² + 1 не делится на 3 ни при каком натуральном n.
Решение:
Переберите остатки от деления на 3.
Задача 19:
Докажите, что n³ + 2 не делится на 9 ни при каком натуральном n.
Решение:
Переберите остатки от деления на 9.
Задача 20:
Докажите, что n³ – n делится на 24 при любом нечетном n.
Решение:
Указание: Докажите, что указанное число делится и на 3, и на 8.
Задача 21:
а) Докажите, что p² – 1 делится на 24, если p – простое число и p > 3.
б) Докажите, что p² – q² делится на 24, если p и q – простые числа, большие 3.
Решение:
Указание: Докажите, что указанные числа делятся и на 3 и на 8.
Задача 22:
Натуральные числа x, y, z таковы, что x² + y² = z². Докажите, что хотя бы одно из этих чисел делится на 3.
Решение:
Если ни x, ни y не делятся на 3, то x² и y² дают остаток 1 от деления на 3. Таким образом, их сумма имеет остаток 2 от деления на 3. Но z² не может иметь такого остатка.
Задача 23:
a и b – натуральные числа, причем число a² + b² делится на 21. Докажите, что оно делится и на 441.
Решение:
Проверьте, что и a и b делятся и на 3 и на 7.
Задача 24:
a, b, c – натуральные числа, причем a + b + c делится на 6. Докажите, что a³ + b³ + c³ тоже делится на 6.
Решение:
Проверьте, что числа x³ и x имеют одинаковые остатки от деления на 6.
Задача 25:
Три простых числа p, q и r, большие 3, образуют арифметическую прогрессию: p = p, q = p + d, r = p + 2d. Докажите, что d делится на 6.
Решение:
Если d – нечетно, то среди чисел p и q есть четное, что невозможно. Если d не делится на 3, то среди чисел p, q и r есть делящееся на 3, что тоже невозможно.
Задача 26:
Докажите, что сумма квадратов трех натуральных чисел, уменьшенная на 7, не делится на 8.
Решение:
Выясните возможные остатки квадратов при делении на 8.
Задача 27:
Сумма трех натуральных чисел, являющихся точными квадратами, делится на 9. Докажите, что из них можно выбрать два, разность которых также делится на 9.
Решение:
Возможные остатки квадратов от деления на 9: 0, 1, 4, 7. Проверьте, что если сумма трех из них делится на 9, то среди них есть два одинаковых.
Задача 28:
Решение:
Так как при нахождении последней цифры очередной степени числа 9 достаточно умножить на 9 лишь последнюю цифру предыдущей степени, то ясно, что за 9 следует 1 (9 9 = 81), а за 1 – 9 (1 9 = 9).
Таким образом, нечетные степени девятки оканчиваются на 9. Поэтому последняя цифра числа 1989 1989 – девятка.
Задача 29:
Решение:
Выпишем последние цифры нескольких начальных степеней двойки: 2, 4, 8, 6, 2, …. Мы видим, что 2 5 так же, как и 2¹, оканчивается на 2. Поскольку очередная цифра полностью определяется последней цифрой предыдущей степени, то произойдет «зацикливание»: 2 6 (как и 2²) оканчивается на 4, 2 7 (как и 2³) – на 8, 2 8 – на 6, 2 9 – на 2 и т.д. Поскольку длина цикла равна 4, то последняя цифра числа 2 50 определяется остатком от деления числа 50 на 4. Так как он равен 2, то последняя цифра числа 2 50 совпадает с последней цифрой числа 2², то есть равна 4.
Задача 30:
Решение:
Задача 31:
Найдите остаток от деления 2¹ºº на 3.
Решение:
Выпишите остатки от деления на 3 нескольких начальных степеней двойки. Докажите, что здесь происходит «зацикливание».
Задача 32:
Найдите остаток от деления 3 1989 на 7.
Решение:
Задача 33:
Докажите, что 2222 5555 + 5555²²²² делится на 7.
Решение:
Вычислите остаток от деления этого числа на 7 и убедитесь, что он равен нулю.
Задача 34:
Найдите последнюю цифру числа 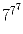
Задача 35:
а) p, p + 10, p + 14 – простые числа. Найдите p.
б) p, 2p + 1, 4p + 1 – простые числа. Найдите p.
Решение:
Рассмотрите остатки от деления на 3. Одно из этих чисел делится на 3. а) p = 3; б) p = 3.
Задача 36:
p и 8p² + 1 – простые числа. Найдите p.
Решение:
Задача 37:
p и p² + 2 – простые числа. Докажите, что p³ + 2 – также простое число.
Решение:
Задача 38:
Докажите, что не существует натуральных чисел a и b таких, что a² – 3b² = 8.
Решение:
Рассмотрите остатки по модулю 3.
Задача 39:
а) Может ли сумма квадратов двух нечетных чисел быть квадратом целого числа?
б) Может ли сумма квадратов трех нечетных чисел быть квадратом целого числа?
Решение:
Проверьте, что остаток квадрата нечетного числа от деления на 4 равен 1, а остаток квадрата четного числа – 0.
Задача 40:
Докажите, что сумма квадратов пяти последовательных натуральных чисел не является точным квадратом.
Решение:
Проверьте, что остаток квадрата нечетного числа от деления на 4 равен 1, а остаток квадрата четного числа – 0.
Задача 41:
p, 4p² + 1 и 6p² + 1 – простые числа. Найдите p.
Ответ: p = 5. Рассмотрите остатки при делении на 5.
Задача 42:
Докажите, что число 100 … 00500 … 001 (в каждой из двух групп по 100 нулей) не является кубом целого числа.
Решение:
Это число дает остаток 7 от деления на 9.
Задача 43:
Докажите, что a³ + b³ + 4 не является кубом целого числа ни при каких натуральных a и b.
Решение:
Выясните, какой остаток может давать число a³ + b³ + 4 от деления на 9.
Задача 44:
Докажите, что число 6n³ + 3 не является шестой степенью целого числа ни при каком натуральном n.
Решение:
Выясните, какой остаток может давать число 6n³ + 3 от деления на 7.
Задача 45:
x, y, z – натуральные числа, причем x² + y² = z². Докажите, что xy делится на 12.
Решение:
Если ни одно из чисел x, y не делится на 3, то z² дает остаток 2 при делении на 3, что невозможно. Заметьте теперь, что квадрат нечетного числа при делении на 8 дает остаток 1, квадрат четного числа, не делящегося на 4, – остаток 4, квадрат числа, делящегося на 4, – остаток 0. Докажите, что либо x и y оба четны, либо среди них есть число, кратное 4.
Докажите что n не делится на 2 в степени n
Задача 1:
Докажите, что a ≡ b (mod m) тогда и только тогда, когда a – b делится на m.
Решение:
Пусть a ≡ b (mod m). Обозначим одинаковый для a и b остаток при делении на m через r. Тогда
Отсюда a – b = m(k 1 – k 2 ) делится на m.
Задача 2:
Если a ≡ b (mod m) и c ≡ d (mod %)%m, то a + c ≡ b + d (mod %)%m.
Решение:
Так как a – b делится на m и c – d делится на m, то (a – b) + (c – d) = (a + c) – (b + d) делится на m, что и требовалось доказать.
Задача 3:
Если a ≡ b (mod %)%m и c ≡ d (mod %)%m, то a – c ≡ b – d (mod %)%m.
Задача 4:
Если a ≡ b (mod %)%m и c ≡ d (mod %)%m, то ac ≡ bd (mod %)%m.
Решение:
ac – bd = ac – bc + bc – bd = (a – b)c + b(c – d) делится на m, что и требовалось доказать.
Задача 5:
Если a ≡ b (mod %)%m, n – натуральное число, то a n ≡ b n (mod %)%m.
Задача 6:
Докажите, что n² + 1 не делится на 3 ни при каком целом n.
Решение:
Ясно, что каждое целое число n сравнимо по модулю 3 либо с 0, либо с 1, либо с 2.
Если n ≡ 0 (mod %)%3, то n² ≡ 0 (mod 3) – (умножение сравнений) и n² + 1 ≡ 1 (mod %)%3 – (сложение сравнений).
Если n ≡ 1 (mod %)%3, то n² + 1 ≡ 2 (mod %)%3.
Если n ≡ 2 (mod %)%3, то n² + 1 ≡ 2 (mod %)%3.
Таким образом, ни в одном случае мы не получим n² + 1 ≡ 0 (mod %)%3.
Задача 7:
Найдите остаток от деления 6¹ºº на 7.
Решение:
Заметим, что 6 ≡ – 1 (mod %)%7. Возводя это сравнение в сотую степень, получаем 6¹ºº ≡ ( – 1)¹ºº (mod %)%7, то есть 6¹ºº ≡ 1 (mod %)%7.
Задача 8:
Докажите, что 30 99 + 61¹ºº делится на 31.
Решение:
30 99 ≡ ( – 1) 99 ≡ – 1 (mod 31) 61¹ºº ≡ ( – 1)¹ºº ≡ 1 (mod 31).
Задача 9:
а) 43¹º¹ + 23¹º¹ делится на 66.
б) a n + b n делится на a + b, если n – нечетное число.
Решение:
б) a n + b n = (a + b)(a n – 1 – a n – 2 b + … + ( – 1) n – 1 b n – 1 )
Задача 10:
Докажите, что 1 n + 2 n + … + (n – 1) n делится на n при нечетном n.
Решение:
Указание: Рассмотрите сумму симметричных слагаемых.
Задача 11:
Докажите, что существует бесконечно много натуральных чисел, не представимых в виде суммы трех точных кубов.
Решение:
Рассмотрите числа вида 8k + 7.
Задача 12:
Докажите, что ни одно из чисел вида 10 3n + 1 нельзя представить в виде суммы двух кубов натуральных чисел.
Решение:
Куб натурального числа сравним по модулю 7 либо с 0, либо с 1, либо с – 1 – проверьте! Поэтому сумма двух кубов сравнима с одним из следующих чисел: – 2, – 1, 0, 1, 2. Заметим, что 10 ≡ 3 (mod %)%7, а 10³ ≡ – 1 (mod %)%7. Поэтому 10 3n + 1 сравнимо либо с 3, либо с – 3 по модулю 7.
Задача 13:
Докажите, что среди 51 целого числа найдутся два, квадраты которых дают одинаковые остатки при делении на 100.
Решение:
Используйте тождество x² – y² = (x – y)(x + y).
Задача 14:
Назовем натуральное число n удобным, если n² + 1 делится на 1000001. Докажите, что среди чисел 1, 2, …, 1000000 четное число удобных.
Решение:
Если x – удобное число, то и 1000001 – x – также удобное.
Задача 15:
а) Может ли квадрат натурального числа оканчиваться на 2?
б) Можно ли, используя только цифры 2, 3, 7, 8 (возможно, по несколько раз), составить квадрат натурального числа?
Решение:
Задача 16:
Какое число нужно добавить к числу (n² – 1)¹ººº (n² + 1)¹ºº¹, чтобы результат делился на n?
Решение:
Например, – 1 или n – 1.
Задача 17:
Найдите остаток от деления на 7 числа 10¹º + 10¹ºº + 10¹ººº + … + 10¹ºººººººººº.
Решение:
Задача 18:
Сколько существует натуральных чисел n, меньших 10000, для которых 2 n – n² делится на 7?
Решение:
Задача 19:
Обозначим через k произведение нескольких (больше одного) первых простых чисел. Докажите, что число а) k – 1; б) k + 1 не является точным квадратом.
Решение:
а) k – 1 = 3p + 2, а по модулю 3 квадраты могут давать лишь остатки 0 или 1.
б) k + 1 = 4q + 3, а по модулю 4 квадраты могут давать лишь остатки 0 или 1.
Задача 20:
Существует ли такое натуральное n, что n² + n + 1 делится на 1955?
Решение:
Нет. n² + n + 1 не может даже делиться на 5.
Задача 21:
Докажите, что 11 n + 2 + 12 2n + 1 делится на 133 при любом натуральном n.
Решение:
Задача 22:
Пусть n – натуральное число такое, что n + 1 делится на 24. Докажите, что сумма всех натуральных делителей n делится на 24.
Решение:
Докажите, что сумма делителей делится и на 3, и на 8.
Задача 23:
а) a 1 = a 2 = 1. Докажите, что ни один из членов последовательности не делится на 4.
б) Докажите, что a n – 22 – составное число при любом n > 10.
Решение:
докажите что n 2 1 не делится на 3 ни при каком натуральном n
Докажите что n 2 1 не делится на 3 ни при каком натуральном n
Задача 15:
Найдите остатки от деления
а) 1989 1990 1991 + 1992³ на 7;
Решение:
Ответ: а) 0; б) 1, так как 9 дает остаток 1 при делении на 8.
Задача 16:
Докажите, что n³ + 2n делится на 3 для любого натурального n.
Решение:
Число n может давать при делении на 3 один из трех остатков: 0, 1, 2. Рассмотрим три случая.
Если n дает остаток 0, то и n³ и 2n делятся на 3 и поэтому n³ + 2n также делится на 3.
Если n дает остаток 1, то n³ дает остаток 1, 2n – остаток 2, а 1 + 2 делится на 3.
Если n дает остаток 2, то n² дает остаток 1, n³ – остаток 2, 2n – остаток 1, а 2 + 1 делится на 3.
Задача 17:
Докажите, что n 5 + 4n делится на 5 при любом натуральном n.
Решение:
Указание: Переберите остатки от деления на 5.
Задача 18:
Докажите, что n² + 1 не делится на 3 ни при каком натуральном n.
Решение:
Переберите остатки от деления на 3.
Задача 19:
Докажите, что n³ + 2 не делится на 9 ни при каком натуральном n.
Решение:
Переберите остатки от деления на 9.
Задача 20:
Докажите, что n³ – n делится на 24 при любом нечетном n.
Решение:
Указание: Докажите, что указанное число делится и на 3, и на 8.
Задача 21:
а) Докажите, что p² – 1 делится на 24, если p – простое число и p > 3.
б) Докажите, что p² – q² делится на 24, если p и q – простые числа, большие 3.
Решение:
Указание: Докажите, что указанные числа делятся и на 3 и на 8.
Задача 22:
Натуральные числа x, y, z таковы, что x² + y² = z². Докажите, что хотя бы одно из этих чисел делится на 3.
Решение:
Если ни x, ни y не делятся на 3, то x² и y² дают остаток 1 от деления на 3. Таким образом, их сумма имеет остаток 2 от деления на 3. Но z² не может иметь такого остатка.
Задача 23:
a и b – натуральные числа, причем число a² + b² делится на 21. Докажите, что оно делится и на 441.
Решение:
Проверьте, что и a и b делятся и на 3 и на 7.
Задача 24:
a, b, c – натуральные числа, причем a + b + c делится на 6. Докажите, что a³ + b³ + c³ тоже делится на 6.
Решение:
Проверьте, что числа x³ и x имеют одинаковые остатки от деления на 6.
Задача 25:
Три простых числа p, q и r, большие 3, образуют арифметическую прогрессию: p = p, q = p + d, r = p + 2d. Докажите, что d делится на 6.
Решение:
Если d – нечетно, то среди чисел p и q есть четное, что невозможно. Если d не делится на 3, то среди чисел p, q и r есть делящееся на 3, что тоже невозможно.
Задача 26:
Докажите, что сумма квадратов трех натуральных чисел, уменьшенная на 7, не делится на 8.
Решение:
Выясните возможные остатки квадратов при делении на 8.
Задача 27:
Сумма трех натуральных чисел, являющихся точными квадратами, делится на 9. Докажите, что из них можно выбрать два, разность которых также делится на 9.
Решение:
Возможные остатки квадратов от деления на 9: 0, 1, 4, 7. Проверьте, что если сумма трех из них делится на 9, то среди них есть два одинаковых.
Задача 28:
Решение:
Так как при нахождении последней цифры очередной степени числа 9 достаточно умножить на 9 лишь последнюю цифру предыдущей степени, то ясно, что за 9 следует 1 (9 9 = 81), а за 1 – 9 (1 9 = 9).
Таким образом, нечетные степени девятки оканчиваются на 9. Поэтому последняя цифра числа 1989 1989 – девятка.
Задача 29:
Решение:
Выпишем последние цифры нескольких начальных степеней двойки: 2, 4, 8, 6, 2, …. Мы видим, что 2 5 так же, как и 2¹, оканчивается на 2. Поскольку очередная цифра полностью определяется последней цифрой предыдущей степени, то произойдет «зацикливание»: 2 6 (как и 2²) оканчивается на 4, 2 7 (как и 2³) – на 8, 2 8 – на 6, 2 9 – на 2 и т.д. Поскольку длина цикла равна 4, то последняя цифра числа 2 50 определяется остатком от деления числа 50 на 4. Так как он равен 2, то последняя цифра числа 2 50 совпадает с последней цифрой числа 2², то есть равна 4.
Задача 30:
Решение:
Задача 31:
Найдите остаток от деления 2¹ºº на 3.
Решение:
Выпишите остатки от деления на 3 нескольких начальных степеней двойки. Докажите, что здесь происходит «зацикливание».
Задача 32:
Найдите остаток от деления 3 1989 на 7.
Решение:
Задача 33:
Докажите, что 2222 5555 + 5555²²²² делится на 7.
Решение:
Вычислите остаток от деления этого числа на 7 и убедитесь, что он равен нулю.
Задача 34:
Найдите последнюю цифру числа 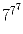
Задача 35:
а) p, p + 10, p + 14 – простые числа. Найдите p.
б) p, 2p + 1, 4p + 1 – простые числа. Найдите p.
Решение:
Рассмотрите остатки от деления на 3. Одно из этих чисел делится на 3. а) p = 3; б) p = 3.
Задача 36:
p и 8p² + 1 – простые числа. Найдите p.
Решение:
Задача 37:
p и p² + 2 – простые числа. Докажите, что p³ + 2 – также простое число.
Решение:
Задача 38:
Докажите, что не существует натуральных чисел a и b таких, что a² – 3b² = 8.
Решение:
Рассмотрите остатки по модулю 3.
Задача 39:
а) Может ли сумма квадратов двух нечетных чисел быть квадратом целого числа?
б) Может ли сумма квадратов трех нечетных чисел быть квадратом целого числа?
Решение:
Проверьте, что остаток квадрата нечетного числа от деления на 4 равен 1, а остаток квадрата четного числа – 0.
Задача 40:
Докажите, что сумма квадратов пяти последовательных натуральных чисел не является точным квадратом.
Решение:
Проверьте, что остаток квадрата нечетного числа от деления на 4 равен 1, а остаток квадрата четного числа – 0.
Задача 41:
p, 4p² + 1 и 6p² + 1 – простые числа. Найдите p.
Ответ: p = 5. Рассмотрите остатки при делении на 5.
Задача 42:
Докажите, что число 100 … 00500 … 001 (в каждой из двух групп по 100 нулей) не является кубом целого числа.
Решение:
Это число дает остаток 7 от деления на 9.
Задача 43:
Докажите, что a³ + b³ + 4 не является кубом целого числа ни при каких натуральных a и b.
Решение:
Выясните, какой остаток может давать число a³ + b³ + 4 от деления на 9.
Задача 44:
Докажите, что число 6n³ + 3 не является шестой степенью целого числа ни при каком натуральном n.
Решение:
Выясните, какой остаток может давать число 6n³ + 3 от деления на 7.
Задача 45:
x, y, z – натуральные числа, причем x² + y² = z². Докажите, что xy делится на 12.
Решение:
Если ни одно из чисел x, y не делится на 3, то z² дает остаток 2 при делении на 3, что невозможно. Заметьте теперь, что квадрат нечетного числа при делении на 8 дает остаток 1, квадрат четного числа, не делящегося на 4, – остаток 4, квадрат числа, делящегося на 4, – остаток 0. Докажите, что либо x и y оба четны, либо среди них есть число, кратное 4.
Метод математической индукции для чайников
Метод полного перебора конечного числа случаев, исчерпывающих все возможности, называется полной индукцией. Этот метод имеет крайне ограниченную область применения в математике, так как обычно математические утверждения касаются бесконечного множества объектов (например, натуральных чисел, простых чисел, квадратов и т.п.) и перебрать их невозможно.
Основы метода математической индукции
Доказательство с помощью метода математической индукции проводится в два этапа:
Метод математической индукции применяется в разных типах задач:
Ниже вы найдете примеры решения задач, иллюстрирующие применение метода математической индукции, а также ссылки на полезные сайты и учебник и небольшой видеоурок по ММИ.
Математическая индукция: задачи и решения
Доказательство кратности и делимости
$$a_n = 2n^3+3n^2+7n, \quad b=6.$$
Доказательство равенств и неравенств
Задача 5. Доказать равенство
Задача 6. Доказать методом математической индукции:
Задача 7. Доказать неравенство:
Задача 8. Доказать утверждение методом математической индукции:
Задача 9. Доказать неравенство:
Вычисление сумм
Задача 11. Доказать методом математической индукции:
Задача 12. Найдите сумму