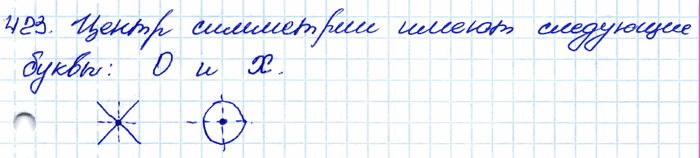докажите что ромб у которого один угол прямой является квадратом
Геометрия 8 класс Атанасян Задачи 399-423
Упражнения 399 — 423 из учебника «Геометрия 8 класс. УМК Атанасян» с ответами и решениями. Глава 5. Четырёхугольники. § 3. Прямоугольник, ромб, квадрат (46. Прямоугольник. 47. Ромб и квадрат. 48. Осевая и центральная симметрии). Геометрия 8 класс Атанасян Задачи 399-423 + ОТВЕТЫ.
Нажмите на спойлер, чтобы посмотреть ответ на задание.
Геометрия 8 класс Атанасян
Глава 5. § 3. Прямоугольник, ромб, квадрат
Задачи №№ 399 — 423:
Задача № 399. □ Докажите, что параллелограмм, один из углов которого прямой, является прямоугольником.
Задача № 400. □ Докажите, что если в четырёхугольнике все углы прямые, то четырёхугольник — прямоугольник.
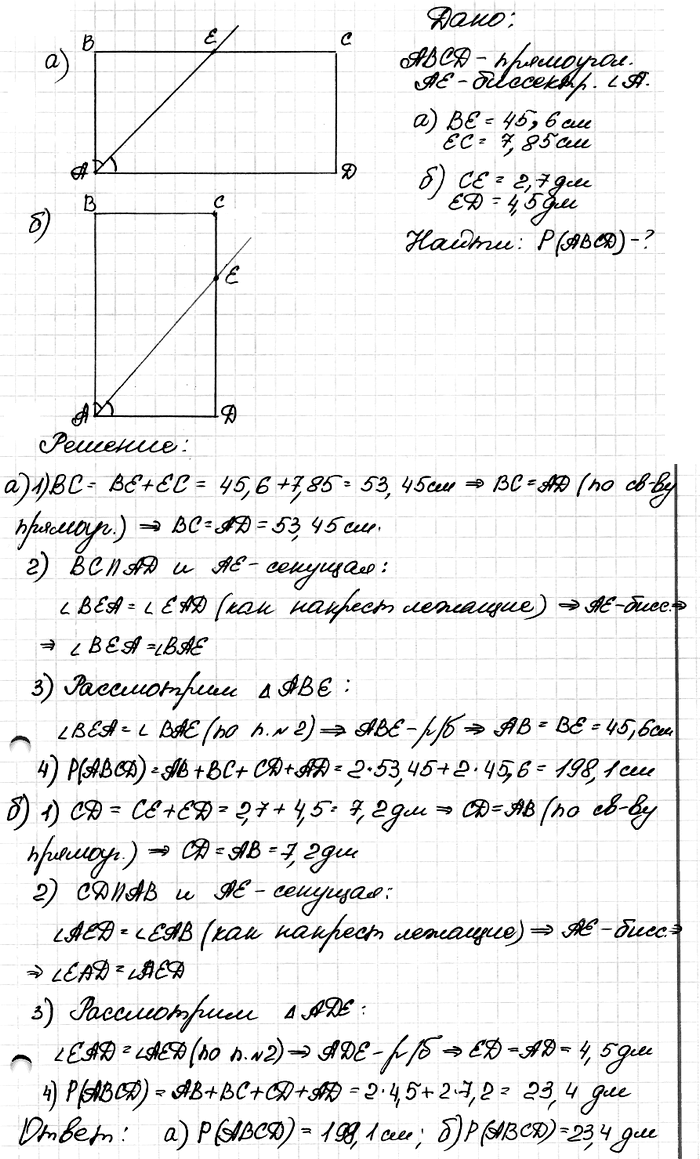
Задача № 401. Найдите периметр прямоугольника ABCD, если биссектриса угла А делит сторону: а) ВС на отрезки 45,6 см и 7,85 см; б) DC на отрезки 2,7 дм и 4,5 дм.
Задача № 402. □ Диагонали прямоугольника ABCD пересекаются в точке О. Докажите, что треугольники AOD и АОВ равнобедренные.
Задача № 403. В прямоугольнике ABCD диагонали пересекаются в точке О. Найдите периметр треугольника АОВ, если ∠CAD = 30°, АС = 12 см.
Задача № 404. □ Докажите, что медиана прямоугольного треугольника, проведённая к гипотенузе, равна половине гипотенузы.
Задача № 405. □ В ромбе одна из диагоналей равна стороне. Найдите: а) углы ромба; б) углы, которые диагонали ромба образуют с его сторонами.
Задача № 406. Найдите периметр ромба ABCD, в котором ∠B = 60°, АС= 10,5 см.
Задача № 407. Найдите углы, которые образуют диагонали ромба с его сторонами, если один из углов ромба равен 45°.
Задача № 408. Докажите, что параллелограмм является ромбом, если: а) его диагонали взаимно перпендикулярны; б) диагональ делит его угол пополам.
Задача № 409. □ Докажите, что ромб, у которого один угол прямой, является квадратом.
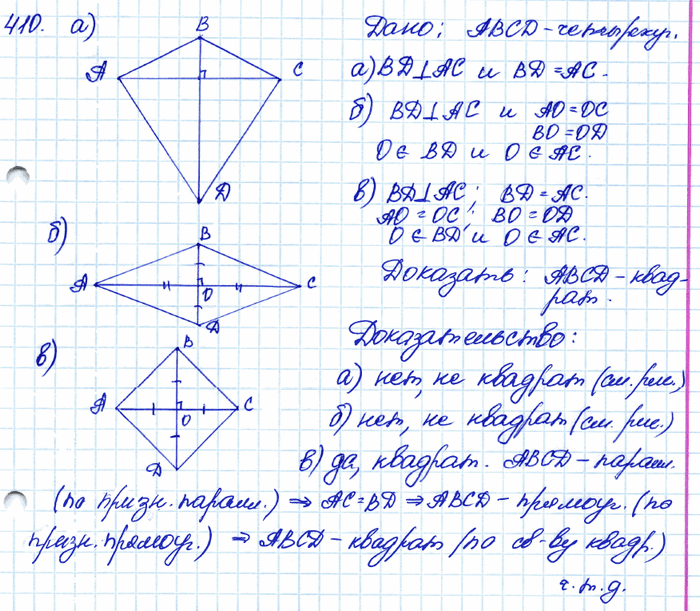
Задача № 410. □ Является ли четырёхугольник квадратом, если его диагонали: а) равны и взаимно перпендикулярны; б) взаимно перпендикулярны и имеют общую середину; в) равны, взаимно перпендикулярны и имеют общую середину?
Задача № 411. □ В прямоугольном треугольнике проведена биссектриса прямого угла. Через точку пересечения этой биссектрисы с гипотенузой проведены прямые, параллельные катетам. Докажите, что полученный четырёхугольник — квадрат.
Задача № 412. Даны равнобедренный прямоугольный треугольник АВС с прямым углом С, катетом АС = 12см и квадрат CDEF, такой, что две его стороны лежат на катетах, а вершина Е — на гипотенузе треугольника. Найдите периметр квадрата.
Задача № 413. □ Постройте прямоугольник: а) по двум смежным сторонам; б) по стороне и диагонали; в) по диагонали и углу между диагоналями.
Задача № 414. □ Постройте ромб: а) по двум диагоналям; б) по стороне и углу.
Задача № 415. □ Постройте квадрат: а) по стороне; б) по диагонали.
Задача № 416. □ Даны две точки А и В, симметричные относительно некоторой прямой, и точка М. Постройте точку, симметричную точке М относительно той же прямой.
Задача № 417. Сколько осей симметрии имеет: а) отрезок; б) прямая; в) луч?
Задача № 419. □ Докажите, что прямая, проходящая через середины противоположных сторон прямоугольника, является его осью симметрии.
Задача № 420. □ Докажите, что прямая, содержащая биссектрису равнобедренного треугольника, проведённую к основанию, является осью симметрии треугольника.
Задача № 421. □ Даны точки А, В и М. Постройте точку, симметричную точке М относительно середины отрезка АВ.
Задача № 422. Имеют ли центр симметрии: а) отрезок; б) луч; в) пара пересекающихся прямых; г) квадрат?
Задача № 423. Какие из следующих букв имеют центр симметрии: А, О, М, X, К?
Вы смотрели: Упражнения из учебника «Геометрия 8 класс. УМК Атанасян» с ответами и решениями. Глава 5. Четырёхугольники. § 3. Прямоугольник, ромб, квадрат. Геометрия 8 класс Атанасян Задачи 399-423 + ОТВЕТЫ.
Докажите, что ромб, у которого один угол прямой, является квадратом.
Ромб-это параллелограмм с равными сторонами.
Так же как и у параллелограмма, у ромба противоположные углы равны. Если одни из углов ромба прямой, то и противоположный ему угол будет прямой. Их сумма равна 90*2=180(град). Оставшиеся два угла ромба в сумме также дают 180 град.(т.к. ромб-это выпуклый четырёхугольник, а сумма внутренних углов выпуклого четырёхугольника составляют 360 град. 360-180=180 град.). Помня о том, что противоположные углы ромба равны, получаем для двух оставшихся углов: 180:2=90 град- градусная мера каждого из углов.
Итак, все углы данного ромба равны 90 град + ромб-это параллелограмм с равными сторонами, следовательно данный ромб-квадрат.
Другие вопросы из категории
Треугольник АВС. Угол А=90 градусов, угол С=30 градусов. АВ=40, найти сторону АС=?
Читайте также
автор учебника анастасян
,перпендикулярная к оси симметрии,отображается на себя.
Б)прямая,проходящая через центр симметрии,отображается на себя.
3.Докажите,что в любом треугольнике либо все углы острые,либо два угла острые,а третий тупой или прямой.
4.Какой треугольник называют остроугольным?Какой треугольник называется тупоугольными?
5.Какой треугольник называется прямоугольным?Как называются стороны прямоугольного треугольника?
6.Докажите,что в треугольнике:
1)против большей стороны лежит больший угол;
2)обратно,против большего угла лежит большая сторона.
7.Докажите,что в прямоугольном треугольнике гипотенуза больше катета.
8.Докажите,что если два угла треугольника равны,то треугольник равнобедренный.
9.Докажите,что каждая сторона треугольника меньше сумма двух других сторон.Что такое неравенство треугольника?
10.Докажите,что сумма двух острых углов прямоугольного треугольника равна 90.
11.Докажите,что катет прямоугольного треугольника,лежащий против угла в 30,равен половине гипотенузы.Сформулируйте и докажите обратное утверждение.
12.Сформулируйте и докажите признак равенства прямоугольных треугольников по гипотенузе и острому углу.
13.Сформулируйте и докажите признак равенства прямоугольных треугольников по гипотенузе и катету.
14.Объясните,какой отрезок называется наклонной,проведенной из данной точки к данной прямой.
15.Докажите,что перпендикуляр,проведенный из точки к прямой,меньше любой наклонной,проведенной из этой же точки к этой прямой.
16.Что называется расстоянием от точки до прямой?
17.Докажите,что все точки каждой из двух параллельных прямых равноудалены от другой прямой.
18.Что называется расстоянием мехду двумя параллельными прямыми?
19.Объясните,как построить треугольник:
а)по двум сторонам и угду между ними
б)по стороне и двум прилежащим к ней углам.
20.Объясните,как построить треугольник по трем сторонам.Всегда ли эта задача имеет решение?