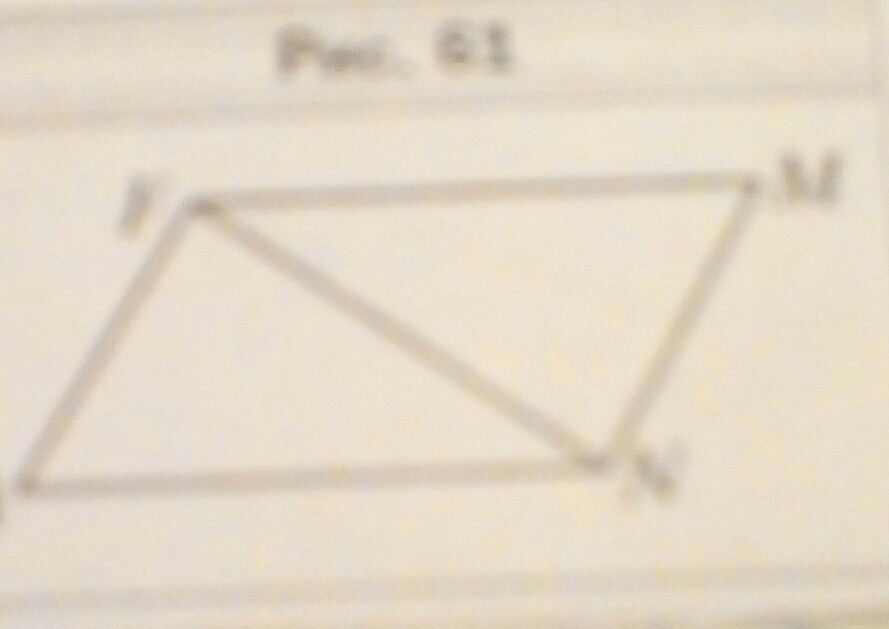
докажите что угол афн равен углу мнф рис 61
Докажите что угол AFN равен углу MNF на рисунке 61 если известно что AN равен FM и AN параллельны FM
По свойству углов при параллельных прямых и секущей накрестлежащие ∠ NFМ ∠ FNA
Следовательно, ∆ AFN=∆ MFN по 1-му признаку равенства треугольников.
Сходственные углы в равных треугольниках равны, ⇒ ∠AFN=∠MNF
Т.к АВСМ вписан в окружность, то угол В+угол АМС=180 °⇒ угол АМС=120°
в тр.АМС: по т.sin:
AM/sin угла АСМ=МС/sin угла МАС=2R
AM/sin (60-α)=МС/sin α=2R
АМ=2Rsin (60-α)
МС=2Rsin α
АМ+МС=2R(sin (60-α)+sin α)=2R*2sin30°cos(30-α)=2Rcos(30-α)
в тр.АBМ: по т.sin:
BМ/sin угла ВАМ=2R
BМ/sin (60+α)=2R
BМ=2Rsin(60+α)=2Rsin(90-(60+α))=2Rsin(90-(30-α))=2Rcos(30-α)
теперь:
АВ/sin60°=2R
АВ=2Rsin60°=2*√138*(√3/2)=√39
S ABC=(a²√3)/4(формула)⇒(39√3)/4
в тр.АМC: по т.cos:
AC²=AM²+МС²-2АМ*МС*сos угла М
39=AM²+МС²-2АМ*МС*сos120°. т.к.сos120°=-1/2
39=AM²+МС²+АМ*МС
.
S тр АМС=S АВСМ-S тр АВС=(49√3)/4-(39√3)/4=(5√3)/2
S тр АМС=1/2AM*MC*sin120°
(5√3)/2=1/2AM*MC*√3/2
AM*MC=10⇒AM²+MC²=29
(AM+MC)²=AM²+МС²+2АМ*МС=29+2*10=49
АМ+МС=7⇒
P=7+2√39
Даны точки А(-1,3,0), В(0 1 2) и модуль СВ, равный 6.
Находим модуль АВ: √(0-(-1))² +(1-3)² + (2-0)²) = √(1 + 4 + 4) = 3.
Модуль СА = 6*cos 30° = 6*(√3/2) = 3√3.
Скалярным произведением двух векторов a и b будет скалярная величина, равная произведению модулей этих векторов, умноженного на косинус угла между ними.
Скалярное произведение векторов СА и СВ равно:
СА х СВ = (3√3)*6*(√3/2) = 27.
Дан прямоугольный треугольник с катетами «а» и «в».
Радиус «R» его описанной окружности равен 6,5, а радиус «r» вписанной окружности равен 2.
Ответ: катеты равны 5 и 12.
Докажите что угол AFN равен углу MNF на рисунке 61 если известно что AN равен FM и AN параллельны FM?
Докажите что угол AFN равен углу MNF на рисунке 61 если известно что AN равен FM и AN параллельны FM.
По свойству углов при параллельных прямых и секущей накрестлежащие∠NFМ∠FNA
Сходственные углы в равных треугольниках равны, ⇒∠AFN = ∠MNF.
На рисунке АВ = BD, угол 1 равен углу 2?
На рисунке АВ = BD, угол 1 равен углу 2.
Докажите что угол ВСА равен углу ВСD.
Известно, что угол 1 равен 102°, угол 2 равен 78° Докажите, что a и b параллельны?
Известно, что угол 1 равен 102°, угол 2 равен 78° Докажите, что a и b параллельны.
Докажите что угол А равен углу Д?
Докажите что угол А равен углу Д.
Докажите что Ад параллельна ВС.
На рисунке 44 угол 1 равен углу 2 угол 2 равен углу 3 Докажите что Прямые A и C параллельны?
На рисунке 44 угол 1 равен углу 2 угол 2 равен углу 3 Докажите что Прямые A и C параллельны.
На рисунке 11?
ДОКАЖИИЕ, что угол В равен углу D.
На рисунке прямые a и b параллельны?
На рисунке прямые a и b параллельны.
Найдите величину угла 2, если угол 1 равен 152градуса.
Докажите, что AB равен CD.
На рисунке прямые а и b параллельны, угол 2 в три раза больше угла 1?
На рисунке прямые а и b параллельны, угол 2 в три раза больше угла 1.
Докажите что AD = DC.
30 / 200 = 0. 15 Вероятность 15%.
Равными векторами называются сонаправленные (направленные в одну сторону) и равные по модулю (по длине). Поэтому вектора АВ и CD не равны, так как они направлены в разные стороны. P. S. А при чем в этой задаче диагонали и их пересечение, я не знаю..