докажите что в равнобедренном треугольнике высоты проведенные

Докажите что в равнобедренном треугольнике высоты проведенные

Здравствуйте!
Докажите что в равнобедренном треугольнике высоты, проведенные к боковым сторонам, равны.
Пожалуйста!

Для начала сформулируем правильно заданную теорему.

Теорема:

Высоты равнобедренного треугольника, которые проведены из его углов при основании к боковым сторонам, — равны.

Доказательство:
Рассмотрим равнобедренный треугольник ВНМ, у которого равны боковые стороны НМ и ВМ. Согласно условию теоремы из углов при его основании В и Н проведены высоты ВО и НР.
Докажем, что эти высоты ВО=НР.
Рассмотрим треугольники ВОМ и НМР.
1) Стороны ВМ=НМ согласно условию как боковые стороны равнобедренного треугольника.
2) Угол М является общим для этих двух треугольников.
Углы ВОМ и НРМ равны, так они являются прямыми вследствие того, что ВО и НР являются высота согласно условию.
Известно, что сумма углов любого треугольника равна 180 градусов.
Из треугольника ВМО: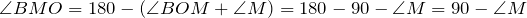
.
Из треугольника НМР: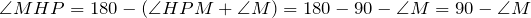
.
Таким образом, получим:
3) .

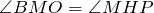
А значит, треугольники ВМО и НМР равны по стороне и двум углам, которые к ней прилегают.

Если треугольники равны, то и все их стороны соответственно равны. А это значит, что и стороны ВО и НР равны.

Доказательство теоремы завершено.

Источник

Свойства высоты равнобедренного треугольника

В данной публикации мы рассмотрим основные свойства высоты равнобедренного треугольника, а также разберем примеры решения задач по данной теме.

Примечание: треугольник называется равнобедренным, если две его стороны равны (боковые). Третья сторона называется основанием.

Свойства высоты в равнобедренном треугольнике

Свойство 1

В равнобедренном треугольнике две высоты, проведенные к боковым сторонам, равны.

Обратная формулировка: Если в треугольнике две высоты равны, значит он является равнобедренным.

Свойство 2

В равнобедренном треугольнике высота, опущенная на основание, одновременно является и биссектрисой, и медианой, и серединным перпендикуляром.

Свойство 3

Если известны стороны/углы равнобедренного треугольника, то:

1. Длина высоты h_a, опущенной на основание a, вычисляется по формуле:

2. Длина высоты h_b, проведенной к боковой стороне b, равняется:

p – это полупериметр треугольника, рассчитывается таким образом:

3. Высоту к боковой стороне можно найти через синус угла и длину стороны треугольника:

Примечание: к равнобедренному треугольнику, также, применимы общие свойства высоты, представленные в нашей публикации – “Высота в треугольнике abc: определение, виды, свойства”.

Пример задачи

Задача 1
Дан равнобедренный треугольник, основание которого равно 15 см, а боковая сторона – 12 см. Найдите длину высоты, опущенной к основанию.

Решение
Воспользуемся первой формулой, представленной в Свойстве 3:

Задача 2
Найдите высоту, проведенную к боковой стороне равнобедренного треугольника длиной 13 см. Основание фигуры равняется 10 см.

Решение
Для начала вычислим полупериметр треугольника:

Теперь применим соответствующую формулу для нахождения высоты (представлена в Свойстве 3):

Источник