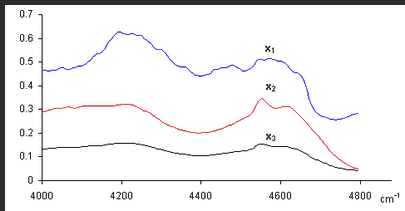
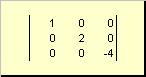
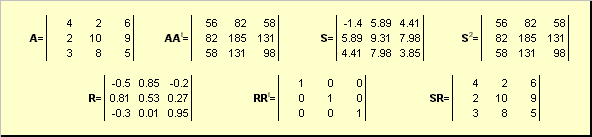
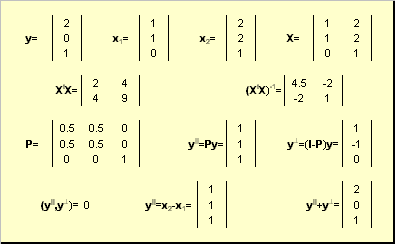
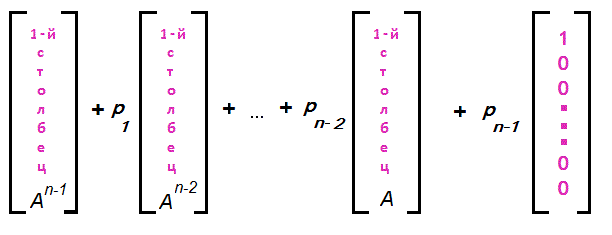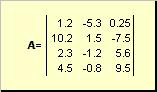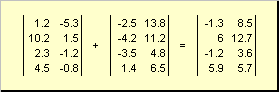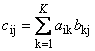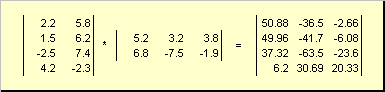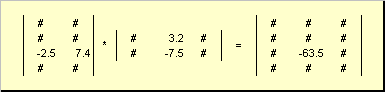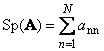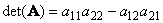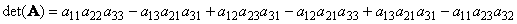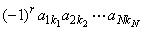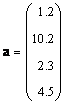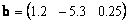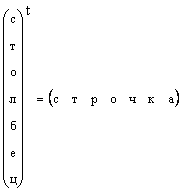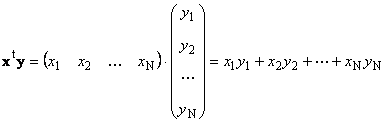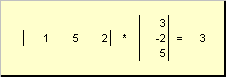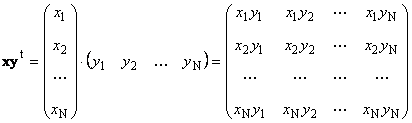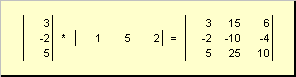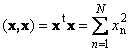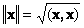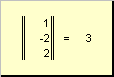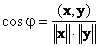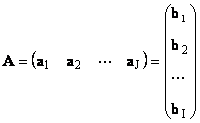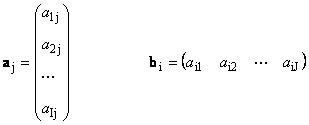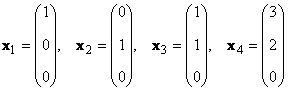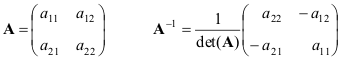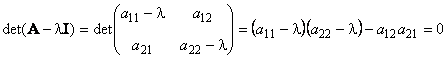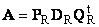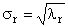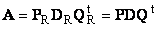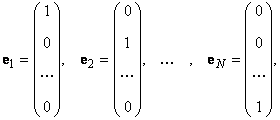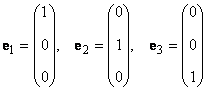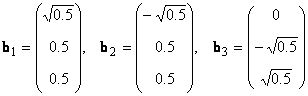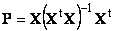докажите что вектор является собственным для матрицы

Решение в приложении.

Должно быть понятно.

Собственные делители числа 500?

Собственные делители числа 500.

Докажите, что число 10001 является составным?

Докажите, что число 10001 является составным.

Собственые делители числа 416?

Собственые делители числа 416.

Найти собственные векторы и собств?

Найти собственные векторы и собств.

Значения линейного оператора, заданного в некотором базисе матрицой А.

Заранее огромное спасибо.

Ответы : а) в * а * сб) с * а * в в) а * с * в г)с * в * а.

Докажите, что число является целым и найдите это целое число?

Докажите, что число является целым и найдите это целое число.

Пожалуйста, очень нужно.

А)Найдите собственную скорость лодки б)Найдите собственную скорость течения реки.

Докажите, что число является целым и найдите его?

Докажите, что число является целым и найдите его.

Докажит, что только одно число состоящее из четного количества одинаковых цифр является простым?

Докажит, что только одно число состоящее из четного количества одинаковых цифр является простым.

7 + 3 = 10 + 4 = + 4 = 4 = 5.

7 + 29 / 8 = 85 / 8 = 10целых 5 / 8.

Источник

Инструменты сайта

Основное

Навигация

Информация

Действия

Содержание

Характеристический полином, собственные числа, собственные векторы матрицы

Характеристический полином

Теорема 1.

Пример. Характеристический полином матрицы Фробениуса

Характеристический полином линейного оператора

определяется как характеристический полином матрицы этого оператора в произвольном базисе линейного пространства, в котором этот оператор задан. Подробнее ☞ ЗДЕСЬ.

Характеристический полином линейного однородного разностного уравнения

Свойства

Теорема 2. Характеристический полином матрицы не меняется

Теорема Гамильтона-Кэли

матрица является корнем своего характеристического полинома.

Доказательство ☞ ЗДЕСЬ.

Собственное число

Пример. Найти спектр матрицы

Доказательство следует из представления характеристического полинома через миноры матрицы и формул Виета. ♦

Имеет место следующее равенство:

Доказательство ☞ ЗДЕСЬ.

Доказательство ☞ ЗДЕСЬ.

Доказательство ☞ ЗДЕСЬ.

Теорема 11. Спектр циклической матрицы

Доказательство ☞ ЗДЕСЬ.

Локализация собственных чисел

Теорема 12. [1]. Собственные числа матрицы являются непрерывными функциями ее элементов. Иначе: пусть

Собственно факт непрерывной зависимости собственных чисел от элементов матрицы следует из представления характеристического полинома из теоремы ☞ ПУНКТА — коэффициенты этого полинома полиномиально (и, следовательно, непрерывно) зависят от элементов матрицы. Далее используем теорему о непрерывной зависимости корней полинома от его коэффициентов.

Выясним теперь на примере, насколько малым может быть возмущение элементов матрицы чтобы сохранились хотя бы количество вещественных корней ее характеристического полинома.

Пример [Уилкинсон] [2]. Найти собственные числа матрицы

Пример. Найти собственные векторы матрицы

Еще один способ нахождения собственного вектора основан на теореме Гамильтона-Кэли.

Пример. Найти собственные векторы матрицы

Пример. Вычислить собственный вектор матрицы

Пример. Найти представление всех собственных векторов матрицы

Доказательство ☞ ЗДЕСЬ.

Теорема Перрона-Фробениуса

Пример. Найти собственное число и вектор Перрона-Фробениуса для матрицы

Пример. Спектр неотрицательной матрицы

Методы вычисления характеристического полинома

А в качестве усугубляющего положение обстоятельства «на заднем плане» маячит проблема точности вычислений коэффициентов характеристического полинома — чувствительность его корней к возмущению его коэффициентов бывает весьма высокой.

Метод Леверье

Пример [Леверье]. Найти характеристический полином матрицы

Пример. Для приведенного выше примера находим собственные числа:

Теорема 21. Характеристический полином явно выражается через суммы Ньютона с помощью следующего представления:

Биографические заметки о Леверье ☞ ЗДЕСЬ.

Метод Крылова

Теорема 22. Определитель

Пример. Найти характеристический полином матрицы примера Леверье

Пример. Найти характеристический полином матрицы

Поиск всех собственных чисел

Существуют методы нахождения спектра матрицы, не требующие предварительного построения характеристического полинома.

QR-алгоритм

Частичная проблема собственных чисел

Теорема 25. Как правило, предел

Как правило, вектор

Пример. Для матрицы

Теперь обсудим исключительные случаи алгоритма.

Пример. Найти максимальное по модулю собственное число матрицы примера Леверье

Пример. Для матрицы

При выполнении условия предположения 2 имеет место равенство

Пример. Для матрицы

Задачи

Источники

[2]. Уилкинсон Дж.Х. Алгебраическая проблема собственных значений. М.Наука. 1970, с.93-94

[3]. Фаддеев Д.К., Фаддеева В.Н. Вычислительные методы линейной алгебры. М.ГИФМЛ. 1960

[4]. Хорн Р., Джонсон Ч. Матричный анализ. М.Мир.1989

Источник

Инструменты сайта

Основное

Навигация

Информация

Действия

Содержание

Ортогональная матрица

Пример. Матрицы

Одно из подмножеств таких матриц имеют специальное название.

Произведение

Теорема. Произведение ортогональных матриц является ортогональной матрицей.

Определитель

Множество ортогональных матриц одинакового порядка образует группу относительно операции умножения.

Будет ли эта группа коммутативной, т.е. абелевой?

Норма

Теорема Кэли

Выражение через экспоненциал кососимметричной матрицы

Ортогональная матрица третьего порядка

Теорема [Эйлер]. Произвольное вращение твердого тела вокруг неподвижной точки, закрепленной в начале координат, задается ортогональной матрицей

Ортогональная матрица четвертого порядка: кватернионы

Характеристический полином, собственные числа

Произведение возратных полиномов будет возвратным полиномом. ♦

Пример. Найти характеристический полином и спектр матрицы

Применения

QR-разложение матрицы

Источники

[1]. Rodrigues O. Des lois géométriques qui régissent les déplacements d’un système solide dans l’espace, et de la variation des coordonnées provenant de ces déplacements considérés indépendamment des causes qui peuvent les produire. Journal de Mathématiques Pures et Appliquées. 1840. V. 5, 380–440

[2]. Проскуряков И.В. Сборник задач по линейной алгебре. М.Наука. 1974; задача N 896.

Источник

Содержание

В этом документе собраны основные сведения из алгебры матриц и векторов, которые используются в хемометрике. Приведенный текст не может служить учебником по матричной алгебре — он скорее является конспектом, справочником в этой области. Более глубокое и систематическое изложение может быть найдено в литературе.

Текст разбит на две части названные — «Базовые сведения» и «Дополнительная информация». В первой части изложены положения, минимально необходимые для понимания хемометрики, а во второй части — факты, которые необходимо знать для более глубокого постижения методов многомерного анализа. Изложение иллюстрируется примерами, выполненными в рабочей книге Excel Matrix.xls, которая сопровождает этот документ.

Ссылки на примеры помещены в текст как объекты Excel. Эти примеры имеют абстрактный характер, они никак не привязаны к задачам аналитической химии. Реальные примеры использования матричной алгебры в хемометрике рассмотрены в других текстах, посвященных разнообразным хемометрическим приложениям.

1. Базовые сведения

1.1 Матрицы

Матрицей называется прямоугольная таблица чисел, например

1.2. Простейшие операции с матрицами

Матрицы можно умножать на числа. При этом каждый элемент умножается на это число. Например —

Рис. 3 Умножение матрицы на число

Две матрицы одинаковой размерности можно поэлементно складывать и вычитать. Например,

Рис. 4 Сложение матриц

В результате умножения на число и сложения получается матрица той же размерности.

Рис. 5 Транспонирование матрицы

1.3. Умножение матриц

Рис.6 Произведение матриц

Рис.7 Элемент произведения матриц

1.4. Квадратные матрицы

Если число столбцов матрицы равно числу ее строк ( I = J = N ), то такая матрица называется квадратной. В этом разделе мы будем рассматривать только такие матрицы. Среди этих матриц можно выделить матрицы, обладающие особыми свойствами.

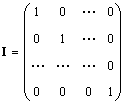
Единичной матрицей (обозначается I, а иногда E ) называется матрица, у которой все элементы равны нулю, за исключением диагональных, которые равны 1, т.е.

Рис. 8 Диагональная матрица

Рис. 9 Верхняя треугольная матрица

Аналогично определяется и нижняя треугольная матрица.

Рис. 10 Симметричная матрица

Матрица называется нормальной если

1.5. След и определитель

Следом квадратной матрицы A (обозначается Tr( A ) или Sp( A )) называется сумма ее диагональных элементов,

Рис. 11 След матрицы

Sp( A + B ) = Sp( A )+ Sp( B ).

Можно показать, что

Другой важной характеристикой квадратной матрицы является ее определитель (обозначается det( A )). Определение определителя в общем случае довольно сложно, поэтому мы начнем с простейшего варианта — матрицы A размерностью (2×2). Тогда

Для матрицы (3×3) определитель будет равен

Рис. 12 Определитель матрицы

Отметим только очевидные свойства:

det( I ) = 1, det( A ) = det( A t ),

det( AB ) = det( A )det( B ).

1.6. Векторы

Можно рассматривать и матрицы, состоящие из одной строки, например

Размерностью вектора называется число его элементов.

Ясно, что всякий вектор-столбец можно превратить в вектор-строку транспонированием, т.е.

1.7. Простейшие операции с векторами

Векторы можно складывать и умножать на числа так же, как это делается с матрицами. Например,

Рис. 13 Операции с векторами

1.8. Произведения векторов

Рис. 14 Внутреннее (скалярное) произведение

Рис. 15 Внешнее произведение

1.9. Норма вектора

Скалярное произведение вектора самого на себя называется скалярным квадратом. Эта величина

Рис. 16 Норма вектора

Векторы называются ортонормированными, если все они нормированы и попарно ортогональны.

1.10. Угол между векторами

Скалярное произведение определяет и угол φ между двумя векторами x и y

Если вектора ортогональны, то cosφ = 0 и φ = π/2, а если они колинеарны, то cosφ = 1 и φ = 0.

1.11. Векторное представление матрицы

Каждую матрицу A размера I × J можно представить как набор векторов

1.12. Линейно зависимые векторы

y = α 1 x 1 + α 2 x 2 +. + α K x K

1.13. Ранг матрицы

Очевидно, что если векторов в наборе больше, чем их размерность ( K > N ), то они обязательно линейно зависимы.

Рангом матрицы (обозначается rank( A )) называется ранг системы векторов, из которых она состоит. Хотя любую матрицу можно представить двумя способами (векторы столбцы или строки), это не влияет на величину ранга, т.к.

1.14. Обратная матрица

Обратная матрица существует не для всех матриц. Необходимым и достаточным условием невырожденности является

Обращение матрицы — это сложная процедура, для выполнения которой существуют специальные программы. Например,

Рис. 17 Обращение матрицы

Приведем формулы для простейшего случая — матрицы 2×2

Если матрицы A и B невырождены, то

1.15. Псевдообратная матрица

Псевдобратная матрица — не единственная и ее вид зависит от способа построения. Например для прямоугольной матрицы можно использовать метод Мура-Пенроуза.

Если число столбцов меньше числа строк, то

A + =(A t A) −1 A t

Рис. 1 7a Псевдообращение матрицы

Если же число столбцов больше числа строк, то

A + =A t (AA t ) −1

1.16. Умножение вектора на матрицу

Рис. 18 Умножение вектора на матрицу

2. Дополнительная информация

2.1. Системы линейных уравнений

2.2. Билинейные и квадратичные формы

2.3. Положительно определенные матрицы

Аналогично определяются отрицательно ( x t Ax x t Ax ≥ 0) и неположительно ( x t Ax ≤ 0) определенные матрицы.

2.4. Разложение Холецкого

Если симметричная матрица A положительно определена, то существует единственная треугольная матрица U с положительными элементами, для которой

Рис. 19 Разложение Холецкого

2.5. Полярное разложение

где S — это неотрицательная симметричная матрица, а R — это ортогональная матрица. Матрицы S и R могут быть определены явно:

Рис. 20 Полярное разложение

2.6. Собственные векторы и собственные значения

2.7. Собственные значения

Рис. 21 Собственные значения

Спектр обладает разнообразными свойствами. В частности

Собственные значения произвольной матрицы могут быть комплексными числами, однако если матрица симметричная ( A t = A ), то ее собственные значения вещественны.

2.8. Собственные векторы

Она имеет нетривиальное решение, поскольку det( A − λ n I ) = 0.

Рис. 22 Собственные вектора

Собственные вектора симметричной матрицы ортогональны.

2.9. Эквивалентные и подобные матрицы

Эквивалентные матрицы имею один и тот же ранг.

Матрица T называется преобразованием подобия.

Подобные матрицы имеют один и тот же ранг, след, определитель и спектр.

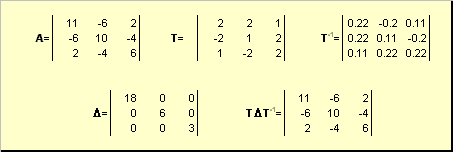
2.10. Приведение матрицы к диагональному виду

Нормальную (в частности симметричную) матрицу A можно привести к диагональному виду преобразованием подобия —

Рис. 23 Приведение к диагональному виду

2.11. Разложение по сингулярным значениям (SVD)

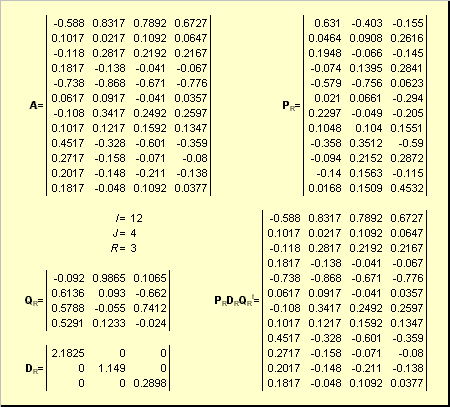
Пусть имеется прямоугольная матрица A размерностью I × J ранга R ( I ≤ J ≤ R ). Ее можно разложить в произведение трех матриц P R ( I × R ), D R ( R × R ) и Q R ( J × R ) —

.

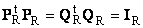
Q R — матрица, образованная R ортонормированными собственными векторами q r матрицы A t A ;

Рис. 24 SVD разложение

Дополняя матрицы P R и Q R ортонормированными столбцами, а матрицу D R нулевыми значениями, можно сконструировать матрицы P ( I × J ), D ( J × J ) и Q ( J × J ) такие, что

2.12. Линейное пространство

2.13. Базис линейного пространства

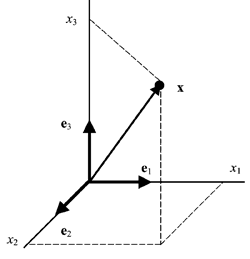
2.14. Геометрическая интерпретация

Рис. 25 Координатное пространство

2.15. Множественность базисов

В линейном пространстве могут быть неограниченное число базисов. Так, в пространстве R 3 помимо обычного ортонормированного базиса

можно установить и другой ортонормированный базис, например

2.16. Подпространство

x = α 1 x 1 + α 2 x 2 +. + α K x K

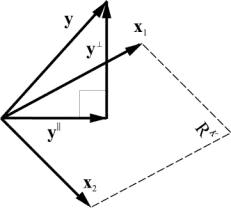
2.17. Проекция на подпространство

Рис. 26 Проекция на подпространство

Проекцию y || можно представить как результат действия проекционной матрицы P

Проекционная матрица определяется как

Рис. 27 Проекционное разложение

Заключение

Матричные методы активно используются при анализе данных, в том числе и хемометрическими методами.

Источник