единственный минус это то что
ЕДИНСТВЕННЫЙ МИНУС
Одноклассник Роман позвал меня на свой юбилей.
Видимся мы редко, не каждый год, но тут такое дело – полтинник не каждый день с человеком случается, никак не отмажешься, нужно идти. Долго изобретал подарок, расщедрился и купил в спорт-товарах резинового злодея в натуральную величину. И Рома с удовольствием побуцкает, да и дети-боксеры у него подрастают, пригодится. Пришли втроем в шикарный ресторан на Арбате: я в пиджаке, жена в платье и злодей с голым торсом. Гостей собралось человек тридцать. Рядом с основным столом, столик поменьше для подарков. Наш был самый заметный, хоть и не самый дорогой. На правах человека знающего юбиляра дольше всех, я выдал первый тост, про то каким Ромчик был славным мальчуганом еще сорок три года назад и все в таком же духе. Праздник набирал обороты, было весело. Подали горячее. Кто-то спросил Юбиляра о работе и Рома с едва скрываемым удовольствием ответил:
— Нормально ты попер.
Рома, изобразив усталую улыбку ковбоя Мальрборо, ответил:
— Нафига мне мигалка? Я еду в тишине, под легкий джаз. С мигалкой, сзади нас едут менты. А платят, не хочу хвастать, но, скажем так, достаточно платят, чтобы иметь возможность на свой скромный юбилей снимать вот такие нескромные залы. Кушайте гости дорогие, поросята остывают.
— Да, слушаю, Валентин Степанович. Ну, в течение… минут двадцати-двадцати пяти должен быть. Да, понял, хорошо.
Не отрывая взгляда от наручных часов, Рома развернулся и не сказав нам ни единого слова, быстрым шагом, почти бегом, понесся к выходу. Ромина жена прикрыла блюдцем содержимое своей тарелки и стараясь ни на кого не смотреть, сказала:
— Работа-то у него отличная, но вот единственный минус, шеф его очень уважает и любит ездить только с ним, так что может дернуть в любую минуту…
Ну а почему бы и нет. Есть еще множество профессий где людей могут дернуть в любую секунду. Он на это согласился, и ему это компенсируют.
Те же фермеры должны кормить скотину каждый день и животным пофиг какой сегодня день, они есть хотят.
Я системный администратор. Поддерживаю ответственные сервера. Меня и с жены снимали и из сортира бежал роняя кал (хорошо что дома, а не в офисе). Работал в 2 часа ночи после литрухи водки с корифаном. Везде хожу со смартфоном и ноутом в рюкзаке. Было так зарылся что в 4 ночи поднял коллегу из дружественной организации поработать в 4 руки. И он меня дёргал. Взаимопомощь, ёпта.
жизненно. я даже понимаю почему он хвастлив сверх меры, это как моральная компенсация такая. жаль чувака.
Ответ Wexler1980 в «Почему мы так хреново живем»
Так, мужик, подержи моё пиво.
Лет 10 назад работал продавцом всякой электронной хрени в киоске на рынке.
И как-то зимним утром пришел на работу, а под дверь насрали. Ну, хм, бывает.
Надо бы убрать.
Беру пластиковый совок, чищу всё это. А оно примерзло к совку.
Что ж, иду искать, как бы это пофиксить.
Через 5 минут возвращаюсь с намерением выкинуть совок. а его нет.
Спёрли.
Февральским утром. На безлюдном рынке. Совок с говном.
ОК.
Честный
На днях заехал в магазин. Купил перекусить, сижу в машине, жуюсь. Подходит мужик бомжеватого типа, стучится в окошко. «Очень сильно извиняюсь, но у вас не будет случайно 4 рубля. Не хватает на чай. » Достаю кошелёк, выгребаю всю мелочь и протягиваю ему.
Он «Нет. Мне только 4 рубля. » Берёт нужную ему сумму и уходит.
Сижу дальше, доедаю, втыкаю в телефон. Опять стук в окно. Опять он. Открываю.
«Спасибо большое, вы меня очень выручили» говорит. И показывает пачку чая.
Впервые мне такой честный попался.
Ответ на пост «Почему мы так хреново живем»
Прошлым летом ковыряюсь в гараже с мотоциклом. Вдруг подходит какой-то тип. Говорит:
— У вас не будет насоса? Я вот с домов напротив (метров триста). Верну минут через двадцать.
Выдаю ему мой любимый ножной насос. Прошло часа два, насоса нет. Расстроился, понял что я лох, и уехал. Вечером приезжаю, охранник меня зовёт:
— Вам просили передать насос, бутылку пива и тысячу извинений. Мне так обидно стало, что я о человеке плохо подумал.
Ответ Kkurochka в «Спалилась»
Вспомнилось.. Лет 12 назад умерла жена у двоюродного брата, оставив его вдовцом с двумя детьми, но речь не об этом. Все само собой помогали чем могли, да и сам он получал ЗП выше, чем по региону. Вкратце дети не нуждались. Первый год к ним в квартиру регулярно ходили из службы опеки и т.д., проверяли условия проживания детей. И задают вопрос младшему: » Всего ли тебе хватает, Юра?» И он возьми да ляпни, ещё жалостливо так: «Все отлично, но вот молочка бы немного. «
Ну вот именно оно кончилось)) По сей день ему это «молочко» вспоминают)
Дтп с мигрантом без страховки.
Нормальные у нас законы, в госдуме о чем думают вообще.
В Москве штраф за парковку 5000, а тут просто торпеды летают и на все клали..
Въехал в зад моей ласточки таксист, разбил мне бампер и себе уже до меня не раз битый, весь в заплатках, страховки нет.
получил штраф 800р и погнал дальше таксовать.
Гайцы руки разводят, типа подавай в суд и тд и тп, хер что получишь в итоге.
То есть, чтоб стать такситом в России,
Зарплаты
С панорамными окнами
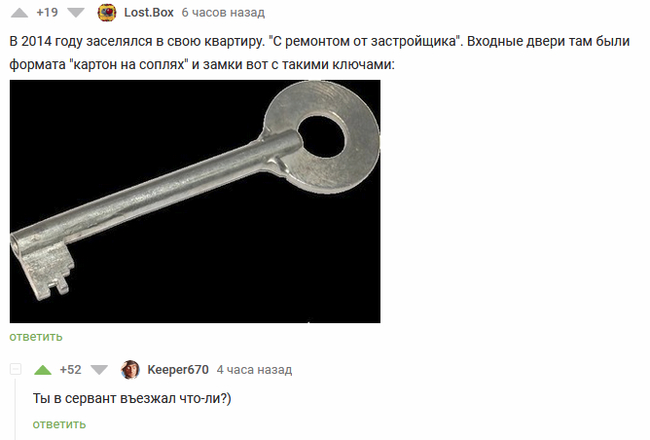
@Lost.Box, @Keeper670, спасибо за короткое возвращение в детство. Реально, у моей бабушки был сервант с примерно таким ключиком, и мне разрешали с ним играть)
Ответ на пост «Важно слышать своих детей»
Что называется, подержите моё пиво.
На ор прибегает бабушка, отвешивает мне смачного леща, а плачущего брата отводит на кухню и даёт ему шоколадку. За попытку оправдаться я получил ещё одного леща.
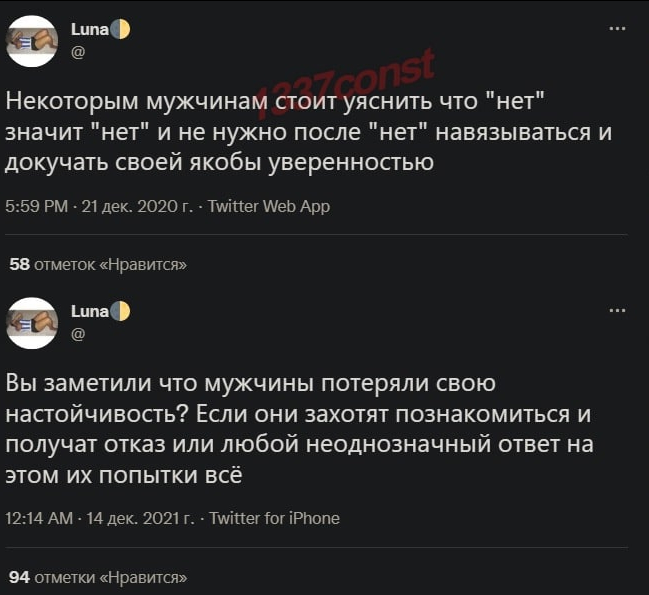
Настойчивость она для кого надо настойчивость
Взрослые снежки
Лет 10 назад друг попросил помочь убрать снег в детсаде его сына. Типа объява висела, кто может из отцов придти помочь. Да легко. Надыбали лопаты и поехали. Батек пришло чел 6-7. Заведующая дала фронт работ и начали мы фигачить снежок. Минут 15-20 поработали и мне в башку стрельнуло. Взял снежок и в другана, тот ответку кинул. И понеслась. Толпа взрослых мужиков носится по территории детсада и нехило так отоваривает друг друга снежками. Упрели зверски. Как не расхерачили стёкла в верандах хз. Вечером друган звонит и говорит, что заведующая с воспиталками чуть детей успокоили, когда те увидели такую вакханалию. Снег убрали. Всем добра)
Так и есть
Однозначно!
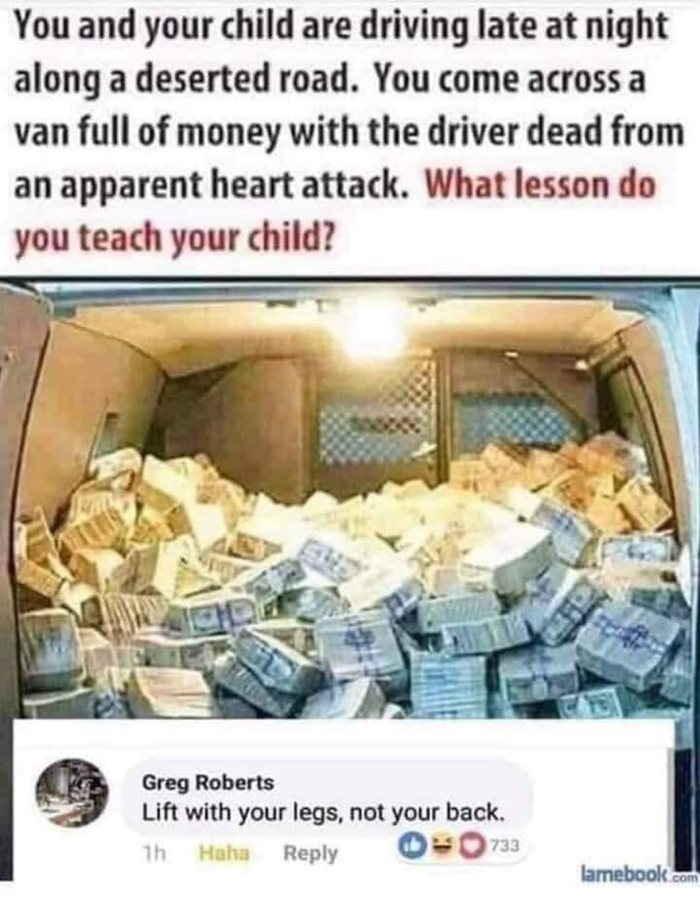
Вы с ребенком едете поздно ночью по заброшенной дороге и натыкаетесь на фургон, полный денег, а его водитель умер с явными признаками сердечного приступа. Какой урок вы преподадите вашему ребенку?
Поднимая тяжести, следует сгибать ноги, а не спину.
Закон есть закон
Ответ Wexler1980 в «Почему мы так хреново живем»
Пф. Когда вселялись с женой в очередную сьемную квартиру, она была без мебели вообще. Ну и на первое время обставиться нужно было хоть минимальным набором, главное дешево и быстро. Одной из этих потребностей был холодильник. Нашел быстро на авито какой-то древний типа бирюза или что-то подобное. Отдали за самовывоз. Ну и со временем он сдох. Заказали новый. В день доставки, зимой, этот решил вынести на помойку. Кое-как вытолкал его из квартиры на площадку лифтов и пошел одеваться, чтоб потом холодос тащить до помойки. Выхожу из квартиры-холодильника нет. Ну на нет и суда нет, зашел обратно охуевший, но довольный.
АХТУНГ! Актуальное предостережение перед новым годом. Отзыв по моему печальному опыту.
Через приложение СберМегаМаркет заказан и полностью оплачен подарок себе на НГ. Oculus Quest 2 за 37087 руб.
Вот он красавец.
Почему минус на минус дает плюс?
1) Почему минус один умножить на минус один равно плюс один?
2) Почему минус один умножить на плюс один равно минус один?
«Враг моего врага — мой друг».
Проще всего ответить: «Потому что таковы правила действий над отрицательными числами». Правила, которые мы учим в школе и применяем всю жизнь. Однако учебники не объясняют, почему правила именно такие. Мы сначала постараемся понять это, исходя из истории развития арифметики, а потом ответим на этот вопрос с точки зрения современной математики.
Без вычитания, конечно, тоже не обойтись. Но на практике мы, как правило, вычитаем из большего числа меньшее, и нет нужды использовать отрицательные числа. (Если у меня есть 5 конфет и я отдам сестре 3, то у меня останется 5 – 3 = 2 конфеты, а вот отдать ей 7 конфет я при всем желании не могу.) Этим можно объяснить, почему люди долго не пользовались отрицательными числами.
В индийских документах отрицательные числа фигурируют с VII века н.э.; китайцы, видимо, начали употреблять их немного раньше. Их применяли для учета долгов или в промежуточных вычислениях для упрощения решения уравнений — это был лишь инструмент для получения положительного ответа. Тот факт, что отрицательные числа, в отличие от положительных, не выражают наличие какой-либо сущности, вызывал сильное недоверие. Люди в прямом смысле слова избегали отрицательных чисел: если у задачи получался отрицательный ответ, считали, что ответа нет вовсе. Это недоверие сохранялось очень долго, и даже Декарт — один из «основателей» современной математики — называл их «ложными» (в XVII веке!).
Что демонстрирует этот нехитрый пример? Во-первых, становится понятна логика, которой определялись правила действий над отрицательными числами: результаты этих действий должны совпадать с ответами, которые получаются другим путем, без отрицательных чисел. Во-вторых, допуская использование отрицательных чисел, мы избавляемся от утомительного (если уравнение окажется посложнее, с большим числом слагаемых) поиска того пути решения, при котором все действия производятся только над натуральными числами. Более того, мы можем больше не думать каждый раз об осмысленности преобразуемых величин — а это уже шаг в направлении превращения математики в абстрактную науку.
Правила действий над отрицательными числами сформировались не сразу, а стали обобщением многочисленных примеров, возникавших при решении прикладных задач. Вообще, развитие математики можно условно разбить на этапы: каждый следующий этап отличается от предыдущего новым уровнем абстракции при изучении объектов. Так, в XIX веке математики поняли, что у целых чисел и многочленов, при всей их внешней непохожести, есть много общего: и те, и другие можно складывать, вычитать и перемножать. Эти операции подчиняются одним и тем же законам — как в случае с числами, так и в случае с многочленами. А вот деление целых чисел друг на друга, чтобы в результате снова получались целые числа, возможно не всегда. То же самое и с многочленами.
Потом обнаружились другие совокупности математических объектов, над которыми можно производить такие операции: формальные степенные ряды, непрерывные функции. Наконец, пришло понимание, что если изучить свойства самих операций, то потом результаты можно будет применять ко всем этим совокупностям объектов (такой подход характерен для всей современной математики).
В итоге появилось новое понятие: кольцо. Это всего-навсего множество элементов плюс действия, которые можно над ними производить. Основополагающими здесь являются как раз правила (их называют аксиомами), которым подчиняются действия, а не природа элементов множества (вот он, новый уровень абстракции!). Желая подчеркнуть, что важна именно структура, которая возникает после введения аксиом, математики говорят: кольцо целых чисел, кольцо многочленов и т. д. Отталкиваясь от аксиом, можно выводить другие свойства колец.
Мы сформулируем аксиомы кольца (которые, естественно, похожи на правила действий с целыми числами), а затем докажем, что в любом кольце при умножении минуса на минус получается плюс.
Заметим, что кольца, в самой общей конструкции, не требуют ни перестановочности умножения, ни его обратимости (т. е. делить можно не всегда), ни существования единицы — нейтрального элемента по умножению. Если вводить эти аксиомы, то получаются другие алгебраические структуры, но в них будут верны все теоремы, доказанные для колец.
А то, что в кольце ровно один ноль (ведь в аксиомах сказано, что такой элемент существует, но ничего не сказано про его единственность!), мы оставим читателю в качестве несложного упражнения.
Почему минус на минус дает плюс?
1) Почему минус один умножить на минус один равно плюс один?
2) Почему минус один умножить на плюс один равно минус один?
«Враг моего врага — мой друг».
Проще всего ответить: «Потому что таковы правила действий над отрицательными числами». Правила, которые мы учим в школе и применяем всю жизнь. Однако учебники не объясняют, почему правила именно такие. Мы сначала постараемся понять это, исходя из истории развития арифметики, а потом ответим на этот вопрос с точки зрения современной математики.
Без вычитания, конечно, тоже не обойтись. Но на практике мы, как правило, вычитаем из большего числа меньшее, и нет нужды использовать отрицательные числа. (Если у меня есть 5 конфет и я отдам сестре 3, то у меня останется 5 – 3 = 2 конфеты, а вот отдать ей 7 конфет я при всем желании не могу.) Этим можно объяснить, почему люди долго не пользовались отрицательными числами.
В индийских документах отрицательные числа фигурируют с VII века н.э.; китайцы, видимо, начали употреблять их немного раньше. Их применяли для учета долгов или в промежуточных вычислениях для упрощения решения уравнений — это был лишь инструмент для получения положительного ответа. Тот факт, что отрицательные числа, в отличие от положительных, не выражают наличие какой-либо сущности, вызывал сильное недоверие. Люди в прямом смысле слова избегали отрицательных чисел: если у задачи получался отрицательный ответ, считали, что ответа нет вовсе. Это недоверие сохранялось очень долго, и даже Декарт — один из «основателей» современной математики — называл их «ложными» (в XVII веке!).
Что демонстрирует этот нехитрый пример? Во-первых, становится понятна логика, которой определялись правила действий над отрицательными числами: результаты этих действий должны совпадать с ответами, которые получаются другим путем, без отрицательных чисел. Во-вторых, допуская использование отрицательных чисел, мы избавляемся от утомительного (если уравнение окажется посложнее, с большим числом слагаемых) поиска того пути решения, при котором все действия производятся только над натуральными числами. Более того, мы можем больше не думать каждый раз об осмысленности преобразуемых величин — а это уже шаг в направлении превращения математики в абстрактную науку.
Правила действий над отрицательными числами сформировались не сразу, а стали обобщением многочисленных примеров, возникавших при решении прикладных задач. Вообще, развитие математики можно условно разбить на этапы: каждый следующий этап отличается от предыдущего новым уровнем абстракции при изучении объектов. Так, в XIX веке математики поняли, что у целых чисел и многочленов, при всей их внешней непохожести, есть много общего: и те, и другие можно складывать, вычитать и перемножать. Эти операции подчиняются одним и тем же законам — как в случае с числами, так и в случае с многочленами. А вот деление целых чисел друг на друга, чтобы в результате снова получались целые числа, возможно не всегда. То же самое и с многочленами.
Потом обнаружились другие совокупности математических объектов, над которыми можно производить такие операции: формальные степенные ряды, непрерывные функции. Наконец, пришло понимание, что если изучить свойства самих операций, то потом результаты можно будет применять ко всем этим совокупностям объектов (такой подход характерен для всей современной математики).
В итоге появилось новое понятие: кольцо. Это всего-навсего множество элементов плюс действия, которые можно над ними производить. Основополагающими здесь являются как раз правила (их называют аксиомами), которым подчиняются действия, а не природа элементов множества (вот он, новый уровень абстракции!). Желая подчеркнуть, что важна именно структура, которая возникает после введения аксиом, математики говорят: кольцо целых чисел, кольцо многочленов и т. д. Отталкиваясь от аксиом, можно выводить другие свойства колец.
Мы сформулируем аксиомы кольца (которые, естественно, похожи на правила действий с целыми числами), а затем докажем, что в любом кольце при умножении минуса на минус получается плюс.
Заметим, что кольца, в самой общей конструкции, не требуют ни перестановочности умножения, ни его обратимости (т. е. делить можно не всегда), ни существования единицы — нейтрального элемента по умножению. Если вводить эти аксиомы, то получаются другие алгебраические структуры, но в них будут верны все теоремы, доказанные для колец.
А то, что в кольце ровно один ноль (ведь в аксиомах сказано, что такой элемент существует, но ничего не сказано про его единственность!), мы оставим читателю в качестве несложного упражнения.
Почему минус на минус дает плюс?
1) Почему минус один умножить на минус один равно плюс один?
2) Почему минус один умножить на плюс один равно минус один?
«Враг моего врага — мой друг».
Проще всего ответить: «Потому что таковы правила действий над отрицательными числами». Правила, которые мы учим в школе и применяем всю жизнь. Однако учебники не объясняют, почему правила именно такие. Мы сначала постараемся понять это, исходя из истории развития арифметики, а потом ответим на этот вопрос с точки зрения современной математики.
Без вычитания, конечно, тоже не обойтись. Но на практике мы, как правило, вычитаем из большего числа меньшее, и нет нужды использовать отрицательные числа. (Если у меня есть 5 конфет и я отдам сестре 3, то у меня останется 5 – 3 = 2 конфеты, а вот отдать ей 7 конфет я при всем желании не могу.) Этим можно объяснить, почему люди долго не пользовались отрицательными числами.
В индийских документах отрицательные числа фигурируют с VII века н.э.; китайцы, видимо, начали употреблять их немного раньше. Их применяли для учета долгов или в промежуточных вычислениях для упрощения решения уравнений — это был лишь инструмент для получения положительного ответа. Тот факт, что отрицательные числа, в отличие от положительных, не выражают наличие какой-либо сущности, вызывал сильное недоверие. Люди в прямом смысле слова избегали отрицательных чисел: если у задачи получался отрицательный ответ, считали, что ответа нет вовсе. Это недоверие сохранялось очень долго, и даже Декарт — один из «основателей» современной математики — называл их «ложными» (в XVII веке!).
Что демонстрирует этот нехитрый пример? Во-первых, становится понятна логика, которой определялись правила действий над отрицательными числами: результаты этих действий должны совпадать с ответами, которые получаются другим путем, без отрицательных чисел. Во-вторых, допуская использование отрицательных чисел, мы избавляемся от утомительного (если уравнение окажется посложнее, с большим числом слагаемых) поиска того пути решения, при котором все действия производятся только над натуральными числами. Более того, мы можем больше не думать каждый раз об осмысленности преобразуемых величин — а это уже шаг в направлении превращения математики в абстрактную науку.
Правила действий над отрицательными числами сформировались не сразу, а стали обобщением многочисленных примеров, возникавших при решении прикладных задач. Вообще, развитие математики можно условно разбить на этапы: каждый следующий этап отличается от предыдущего новым уровнем абстракции при изучении объектов. Так, в XIX веке математики поняли, что у целых чисел и многочленов, при всей их внешней непохожести, есть много общего: и те, и другие можно складывать, вычитать и перемножать. Эти операции подчиняются одним и тем же законам — как в случае с числами, так и в случае с многочленами. А вот деление целых чисел друг на друга, чтобы в результате снова получались целые числа, возможно не всегда. То же самое и с многочленами.
Потом обнаружились другие совокупности математических объектов, над которыми можно производить такие операции: формальные степенные ряды, непрерывные функции. Наконец, пришло понимание, что если изучить свойства самих операций, то потом результаты можно будет применять ко всем этим совокупностям объектов (такой подход характерен для всей современной математики).
В итоге появилось новое понятие: кольцо. Это всего-навсего множество элементов плюс действия, которые можно над ними производить. Основополагающими здесь являются как раз правила (их называют аксиомами), которым подчиняются действия, а не природа элементов множества (вот он, новый уровень абстракции!). Желая подчеркнуть, что важна именно структура, которая возникает после введения аксиом, математики говорят: кольцо целых чисел, кольцо многочленов и т. д. Отталкиваясь от аксиом, можно выводить другие свойства колец.
Мы сформулируем аксиомы кольца (которые, естественно, похожи на правила действий с целыми числами), а затем докажем, что в любом кольце при умножении минуса на минус получается плюс.
Заметим, что кольца, в самой общей конструкции, не требуют ни перестановочности умножения, ни его обратимости (т. е. делить можно не всегда), ни существования единицы — нейтрального элемента по умножению. Если вводить эти аксиомы, то получаются другие алгебраические структуры, но в них будут верны все теоремы, доказанные для колец.
А то, что в кольце ровно один ноль (ведь в аксиомах сказано, что такой элемент существует, но ничего не сказано про его единственность!), мы оставим читателю в качестве несложного упражнения.