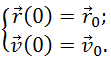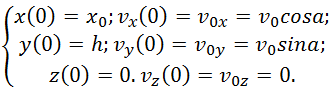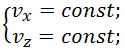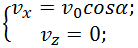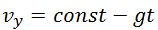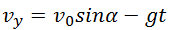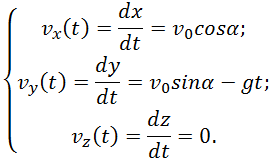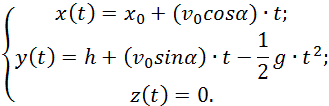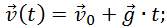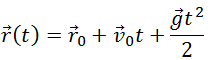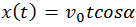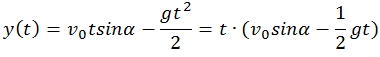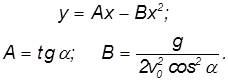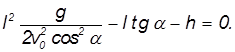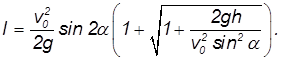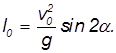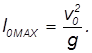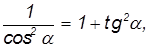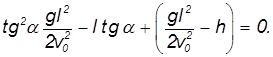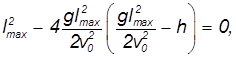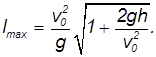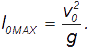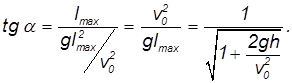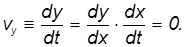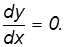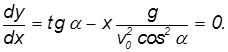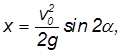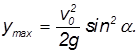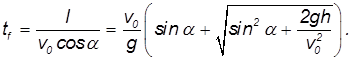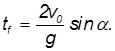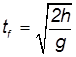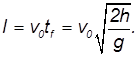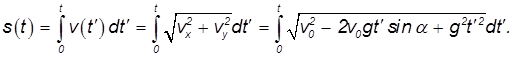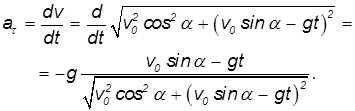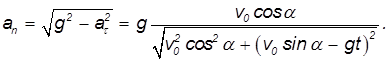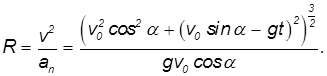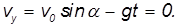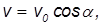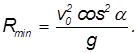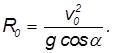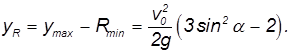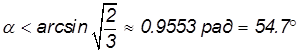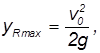горизонтальная составляющая скорости что это
Движение тела, брошенного горизонтально
теория по физике 🧲 кинематика
Если тело бросить горизонтально с некоторой высоты, оно будет одновременно падать и двигаться вперед. Это значит, что оно будет менять положение относительно двух осей: ОХ и ОУ. Относительно оси ОХ тело будет двигаться с постоянной скоростью, а относительно ОУ — с постоянным ускорением.
Кинематические характеристики движения
Графически движение горизонтально брошенного тела описывается следующим образом:
Модуль мгновенной скорости в момент времени t можно вычислить по теореме Пифагора:
Подставив в эту формулу значения проекций мгновенной скорости в момент времени t, получим:
Минимальная скорость в течение всего времени движения равна начальной скорости: vmin = v0.
Максимальной скорости тело достигает в момент приземления. Поэтому максимальной скоростью тела в течение всего времени движения является его конечная скорость: vmax = v.
Время падения — время, в течение которого перемещалось тело до момента приземления. Его можно выразить через формулу высоты при равноускоренном прямолинейном движении:
h0 — высота, с которой тело бросили в горизонтальном направлении.
Дальность полета — перемещение тела относительно ОХ. Обозначается буквой l. Так как относительно ОХ тело движется с постоянной скоростью, для вычисления дальности полета можно использовать формулу перемещения при равномерном прямолинейном движении:
Выразив время падения через высоту и ускорение свободного падения, формула для определения дальности полета получает следующий вид :
Горизонтальное смещение тела — смещение тела вдоль оси ОХ. Вычислить горизонтальное смещение тела в любой момент времени t можно по формуле координаты x:
Учитывая, что x0 = 0, и проекция ускорения свободного падения на ось ОХ тоже равна нулю, а проекция начальной скорости есть модуль этой скорости, данная формула принимает вид:
Мгновенная высота — высота, на которой находится тело в выбранный момент времени t. Она вычисляется по формуле координаты y:
Пример №1. Из окна, расположенного 5 м от земли, горизонтально брошен камень, упавший на расстоянии 8 м от дома. С какой скоростью был брошен камень?
Так как нам известна высота места бросания и дальность полета, начальную скорость тела можно вычислить по формуле:
Выразим начальную скорость и вычислим ее:
Горизонтальный бросок тела с горы
Горизонтальный бросок тела с горы — частный случай горизонтального броска. От него он отличается увеличенным расстоянием между местом бросания и местом падения. Это увеличение появляется потому, что плоскость находится под наклоном. И чем больше этот наклон, тем больше времени требуется телу, чтобы приземлиться.
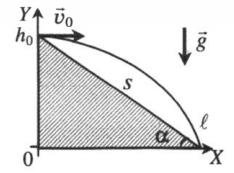
График горизонтального броска тела с горы
α — угол наклона плоскости к горизонту, s — расстояние от места бросания до места падения
Дальность полета — смещение тела относительно оси ОХ от места бросания до места падения. Она равна произведению расстояния от места бросания до места падения и косинуса угла наклона плоскости к горизонту:
Начальная высота — высота, с которой было брошено тело. Обозначается h0. Начальная высота равна произведению расстояния от места бросания до места падения и синусу угла наклона плоскости к горизонту:
Пример №2. На горе с углом наклона 30 о бросают горизонтально мяч с начальной скоростью 15 м/с. На каком расстоянии от точки бросания вдоль наклонной плоскости он упадет?
Выразим это расстояние через дальность полета:
Дальность полета выражается по формуле:
Подставим ее в формулу для вычисления расстояния от точки бросания до точки падения:
Выразим с учетом формулы начальной высоты:
Поделим обе части выражения на общий множитель s:
Подставим известные значения:
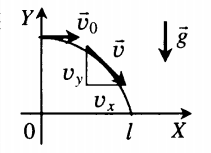
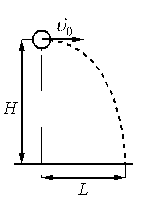
Шарик, брошенный горизонтально с высоты H с начальной скоростью υ 0, за время t пролетел в горизонтальном направлении расстояние L (см. рисунок).
В другом опыте на этой же установке шарик массой 2m бросают со скоростью 2 υ 0.
Что произойдёт при этом с временем полёта, дальностью полёта и ускорением шарика? Сопротивлением воздуха пренебречь. Для каждой величины определите соответствующий характер её изменения:
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
Алгоритм решения
Решение
Время полета тела, брошенного горизонтально, определяется формулой:
Исходя из формулы, время никак не зависит от начальной скорости и массы тела. Поэтому оно при увеличении начальной скорости и массы вдвое никак не изменится.
Дальность полета тела, брошенного горизонтально, определяется формулой:
Исходя из формулы, дальность полета зависит от начальной скорости прямо пропорционально. Поэтому, если начальная скорость тела будет увеличена вдвое, дальность полета тоже увеличится (вдвое). От массы дальность полета никак не зависит.
Ускорение свободного падения — величина постоянная для нашей планеты. Поэтому изменение начальной скорости никак не повлияет на него. Ускорение не изменится.
Значит, верный ответ — 313.
pазбирался: Алиса Никитина | обсудить разбор | оценить
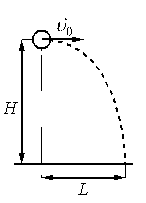
Шарик, брошенный горизонтально с высоты H с начальной скоростью υ 0, за время t пролетел в горизонтальном направлении расстояние L (см. рисунок).
Что произойдёт с временем полёта, дальностью полёта и ускорением шарика, если на этой же установке уменьшить начальную скорость шарика в 2 раза? Сопротивлением воздуха пренебречь. Для каждой величины определите соответствующий характер её изменения:
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
Алгоритм решения
Решение
Время полета тела, брошенного горизонтально, определяется формулой:
Исходя из формулы, время никак не зависит от начальной скорости. Поэтому оно при уменьшении начальной скорости вдвое не изменится.
Дальность полета тела, брошенного горизонтально, определяется формулой:
Исходя из формулы, дальность полета зависит от начальной скорости прямо пропорционально. Поэтому, если начальная скорость тела будет уменьшена вдвое, дальность полета тоже уменьшится (вдвое).
Ускорение свободного падения — величина постоянная для нашей планеты. Поэтому изменение начальной скорости никак не повлияет на него. Ускорение не изменится.
Значит, верный ответ — 323.
pазбирался: Алиса Никитина | обсудить разбор | оценить
2.7. Движение тела, брошенного под углом к горизонту
Рис. 2.16. Движение тела, брошенного под углом к горизонту
Вывод уравнений движения материальной точки в поле силы тяжести
Напишем уравнение движения (уравнение второго закона Ньютона):
Как уже было сказано, мы учитываем только силу тяжести 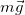
Масса тела в уравнении движения сокращается
это означает, что тела — материальные точки — любых масс при одних и тех же начальных условиях будут двигаться в однородном поле тяжести одинаково. Спроектируем уравнение (2.7.2) на оси декартовой системы координат. Горизонтальная ось ОХ показана на рис. 13 пунктиром, ось OY проведем через точку О вертикально вверх, а горизонтальную ось OZ, также проходящую через точку О, направим перпендикулярно вектору 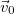
Вертикальным направлением, по определению, называется направление вектора 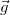
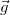
Рис. 2.17. Движение тела, брошенного под углом к горизонту.
Добавим к уравнениям движения начальные условия, которые определяют положение и скорость тела в начальный момент времени t0, пусть t0 = 0. Тогда, согласно рис. 2.7.4
Или в проекциях на оси координат:
Если производная некоторой функции равна нулю, то функция постоянна, соответственно из первого и третьего уравнений (2.7.3) получаем:
Константы находятся из начальных условий, а именно: из первого и третьего уравнений (2.7.5) следует, что в любой момент времени
Во втором уравнении (2.7.3) производная равна константе, откуда следует, что функция зависит от своего аргумента линейно, то есть
Эта константа также находится из начальных условий. Подставляя в (2.7.8) t = 0 и сравнивая результат (vy(0) = const) cо вторым уравнением в (2.7.5) получаем
Объединяя (2.7.7) и (2.7.9), получаем окончательные выражения для зависимостей проекций скорости на оси координат от времени:
Для определения зависимостей от времени координат тела необходимо выполнить еще одно интегрирование — проинтегрировать по времени уравнения (2.7.10) с учетом начальных условий (2.7.5). Используя ту же логику: если производная равна нулю, то функция постоянна, если производная постоянна, то функция зависит от своего аргумента линейно, и подбирая константы так, чтобы удовлетворить начальные условия, можно получить следующий результат:
Третье уравнение (2.7.11) показывает, что траектория тела плоская, целиком лежит в плоскости XOY, это вертикальная плоскость, определяемая векторами 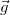
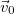
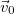
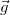
Если три уравнения (2.7.10) умножить на орты осей 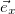
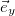

Формулы (2.7.12) и (2.7.13) можно было получить сразу, непосредственно из (2.7.2), если учесть, что ускорение свободного падения есть 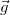
Из (2.7.13) в частности видно, что радиус-вектор является суммой трех векторов, складывающихся по обычным правилам, что наглядно показано на рис. 2.18.
Рис. 2.18. Представление радиус-вектора r(t) в произвольный момент времени t в виде суммы трех векторов
Эти векторы представляют собой:
Здесь отчетливо проявляется принцип независимости движений, известный в других областях физики как принцип суперпозиции (наложения). Вообще говоря, согласно принципу суперпозиции результирующий эффект нескольких воздействий представляет собой сумму эффектов от каждого воздействия в отдельности. Он является следствием линейности уравнений движения.
Видео 2.3. Независимость горизонтального и вертикального перемещений при движении в поле тяжести.
Поместим начало отсчета в точку бросания. Теперь 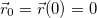
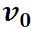
Рис. 2.19. Проекции начальной скорости на координатные оси
Спроецируем 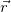
Траектория полета. Если из системы полученных уравнений исключить время t, то получим уравнение траектории:
Это уравнение параболы, ветви которой направлены вниз.
Дальность полета при стрельбе с высоты h. В момент падения тела 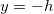
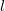
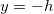
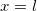
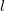
У квадратного уравнения имеется два решения (в данном случае — положительное и отрицательное). Нам нужно положительное решение. Стандартное выражение для корня квадратного уравнения нашей задачи может быть приведено к виду:
При 
Из нее следует, в частности, что максимальная дальность полета
достигается при 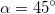
Максимальная дальность полета. При выстреле с горы высотой 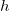
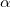
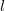
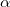
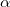
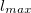
Обратимся снова к квадратному уравнению относительности дальности полета 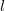

перепишем его в виде:
Мы снова получили квадратное уравнение, на этот раз — для неизвестной величины 
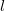
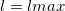
откуда следует результат
При 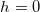
Обычно высота 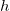
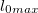
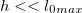
то есть дальность выстрела увеличивается примерно на высоту подъема пушки.
Когда l = lmax, и a = amax, как уже отмечалось, дискриминант квадратного уравнения равен нулю, соответственно, его решение имеет вид:
Поскольку тангенс меньше единицы, угол, при котором достигается максимальная дальность полета, меньше 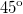
Максимальная высота подъёма над начальной точкой. Эта величина может быть определена из равенства нулю вертикальной составляющей скорости в верхней точке траектории
При этом горизонтальная составляющая скорости 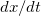
Дифференцируя ранее полученное уравнение траектории, приходим к уравнению:
что при подстановке в уравнение траектории полета приводит к формуле:
Продолжительность полета. Поскольку горизонтальная составляющая скорости не меняется, то продолжительность полета 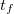
При 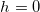
При 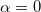
равно времени падения тела с высоты 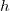
Путь, пройденный телом. За время t тело проходит путь
Интеграл берется в элементарных функциях, но из-за громоздкости ответа мы не выписываем здесь соответствующее выражение.
Расстояние от места выстрела. К моменту времени t расстояние от места выстрела определяется модулем радиус-вектора:
Радиус кривизны траектории в заданной точке. В отсутствие сопротивления воздуха тело движется с постоянным ускорением силы тяжести 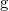
Тангенциальная компонента ускорения, характеризующая быстроту изменения модуля скорости, равна
Нормальная компонента ускорения, изменяющая направление скорости тела, определяется соотношением:
Используя связь нормальной компоненты ускорения с радиусом кривизны, находим 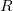
В числителе этого выражения в степени 3/2 стоит модуль скорости. Поэтому, даже не вычисляя производной, мы можем ответить на вопрос, в какой точке траектории кривизна максимальна, а радиус кривизны C = 1/R минимален. Радиус кривизны R достигает минимума там, где минимальна скорость, а это имеет место в верхней точке траектории, в которой вертикальная компонента скорости равна нулю:
Еще раз напомним, что горизонтальная компонента скорости, всюду имеет одно и то же значение. В верхней точке модуль скорости равен горизонтальной составляющей скорости
Для сравнения: радиус кривизны 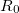
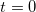
Положение центра кривизны (для высшей точки траектории). По определению радиуса кривизны центр кривизны для высшей точки траектории находится прямо под этой точкой на высоте
Напомним, что мы отсчитываем вертикальные расстояния от уровня пушки, а не от уровня моря.
эта координата отрицательна, то есть центр кривизны находится ниже пушки. Максимально высокое положение центр кривизны занимает при 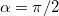
что совпадает с верхней точкой траектории. Тогда радиус кривизны равен нулю. Это значит, что кривизна в этой точке бесконечна, в чем легко убедиться, представив себе траекторию при вертикальном движении снаряда.
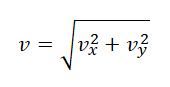
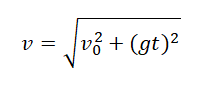
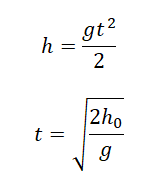
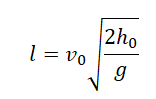
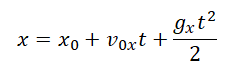
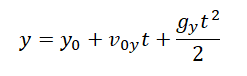
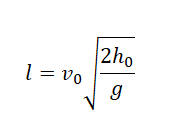
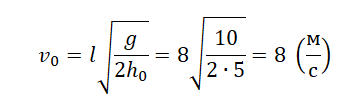
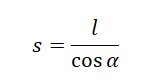
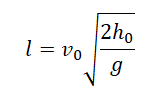
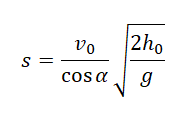
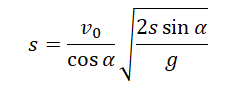
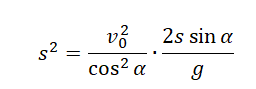
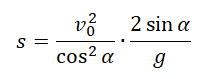
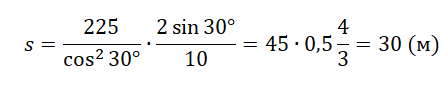

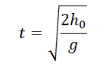
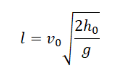

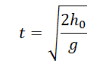
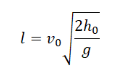

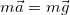
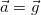
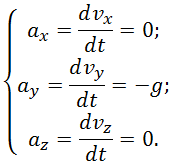
.png)