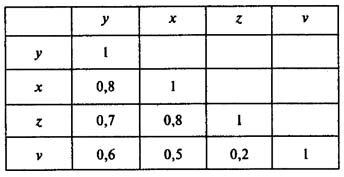
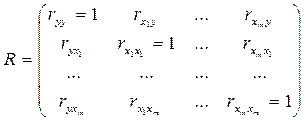говорят что факторы включенные в уравнение регрессии мультиколлинеарны если

Мультиколлинеарность

Коэффициенты интеркорреляции (т. е. сила связи между объясняющими переменными) позволяют исключить из модели регрессии дублирующие факторы. Две переменных явно коллинеарны, когда они находятся между собой в линейной зависимости, если коэффициент корреляции > 0,7.

Поскольку одним из условий нахождения уравнения множественной регрессии является независимость действия факторов, коллинеарность факторов нарушает это условие. Если факторы модели коллинеарны, то они дублируют друг друга и один из них рекомендуется исключить из регрессии.

Предпочтение в эконометрике отдается не фактору, более сильно связанному с результатом, а фактору, который при сильной связи с результатом имеет наименьшую тесноту связи с другими факторами. Т.е. коэффициент корреляции между факторами меньше 0,3 или, в идеале, близок к нулю. В этом условии проявляется специфика множественной регрессии как метода исследования комплексного влияния факторов на результат в условиях их независимости друг от друга.

Матрица парных коэффициентов корреляции

Пусть, например, при изучении зависимости у = f(x, z, v) матрица парных коэффициентов корреляции оказалась следующей:

Факторы х и z дублируют друг друга, т.к. связь между ними сильная (больше 0,7). В анализ нужно включить фактор z, а не х, так как корреляция z с результатом у слабее, чем корреляция фактора х с у, но значительно слабее межфакторная связь Rzv

Источник

Говорят что факторы включенные в уравнение регрессии мультиколлинеарны если

Регрессионный анализ экономических переменных составляет основу эконометрических исследований. Хорошее уравнение регрессии может дать экономисту много важной информации об интересующем его экономическом объекте, а также даёт возможность прогнозирования показателей в зависимости от значений, влияющих на них факторов.

В регрессионном анализе многое зависит от выбора наиболее подходящего вида уравнения: линейное оно или нелинейное; если нелинейное, то какого именно вида. Но все же определяющим этапом исследования, предшествующим регрессионному анализу, являются процедуры, направленные на выбор факторов для уравнения регрессии. Рассмотрению и комбинированию различных методик отбора информативных факторов для регрессионного анализа посвящена данная статья.

При построении модели регрессии к факторам, включаемым в модель, предъявляется ряд требований:

1) каждый фактор должен быть обоснован теоретически;

2) в модель включаются только те факторы, которые могут быть количественно измерены или отождествлены с цифровыми метками (представлены в виде фиктивных переменных);

3) в модель нельзя включать совокупный фактор и факторы, его образующие;

4) факторы должны быть тесно связаны с исследуемой переменной;

5) факторы должны быть линейно независимы друг от друга.

Три последних требования можно коротко сформулировать так: факторы, включаемые в модель регрессии, должны быть тесно связаны с исследуемой переменной и слабо – с другими факторами модели.

При построении множественной линейной регрессии часто сталкиваются с наличием линейной или близкой к ней связи между всеми или некоторыми объясняющими переменными. Это явление называется мультиколлинеарностью. В математической статистике этот термин используется для обозначения тесной корреляционной взаимосвязи между отбираемыми для анализа факторами, совместно воздействующими на общий результат. Эта связь затрудняет оценивание параметров регрессии. Впервые на проблему мультиколлинеарности обратил внимание норвежский математик Нобелевский лауреат Рагнар Фриш [6].

В данной работе мы рассмотрим некоторые подходы к решению проблемы мультиколлинеарности экзогенных (объясняющих) факторов.

Мультиколлинеарность объясняющих переменных вызывает уменьшение точности оценивания или даже невозможность оценки влияния тех или иных переменных на результирующую переменную. Причина заключается в том, что вариации в исходных данных перестают быть независимыми и поэтому невозможно выделить влияние каждой независимой переменной в отдельности на зависимую переменную. Продемонстрируем это на простом примере. Пусть исследуется зависимость себестоимости от объема производства и введенных в действие основных фондов. Следует ожидать, что объем производства зависит также от основных фондов. Если мы обе переменные выберем в качестве объясняющих, то, очевидно, коэффициенты регрессии не будут точно отражать зависимость себестоимости от обоих факторов, так как основные фонды оказывают дополнительное влияние на себестоимость через объем производства.

Виды мультиколлинеарности: строгая (perfect) мультиколлинеарность – наличие линейной функциональной связи между независимыми переменными и нестрогая (imperfect) мультиколлинеарность – наличие сильной линейной корреляционной связи между независимыми переменными. Заметим, что корреляционные связи есть всегда. Проблема мультиколлинеарности – проблема силы проявления корреляционных связей.

Строгая мультиколлинеарность нарушает одно из основных условий теоремы Гаусса-Маркова [6] и делает построение регрессии невозможным. Нестрогая мультиколлинеарность затрудняет работу, но не препятствует получению правильных выводов.

Каковы основные причины возникновения мультиколлинеарности?

1. Ошибочное включение в уравнение двух или более линейно зависимых переменных.

2. В модели использованы факторные признаки, являющиеся составными элементами друг друга.

3. Исходные данные представлены временными рядами, имеющими одинаковые тенденции.

Мультиколлинеарность может проявляться и при отсутствии явных парных корреляционных зависимостей между переменными, так как мультиколлинеарность – ситуация линейной зависимости между объясняющими переменными. Однако вовсе необязательно эта зависимость должна быть парной.

При наличии мультиколлинеарности значимость отдельных коэффициентов регрессии уменьшается, так как стандартные ошибки становятся больше, что приводит к меньшей надежности полученных оценок.

Уменьшение значений t-статистики может выражаться в неверном с содержательной точки зрения знаке коэффициента регрессии. При мультиколлинеарности коэффициенты становятся неустойчивыми, поскольку в этом случае сложно отделить влияние одной переменной от влияния другой. Наличие доминантной переменной (коррелированной с зависимой переменной) делает коэффициенты при остальных объясняющих переменных незначимыми.

Выделим наиболее характерные признаки мультиколлинеарности:

1. Оценки становятся очень чувствительными к незначительному изменению результатов наблюдений и объёма выборки.

2. Оценки имеют большие стандартные ошибки, малую значимость, в то время как модель в целом является значимой и обладает хорошей объясняющей способностью (хорошие значения F-статистики и коэффициента детерминации R2).

3. Оценки коэффициентов имеют неправильные с точки зрения теории (и логики) знаки или неоправданно большие значения. Коэффициенты, которые по логике должны быть значимы, оказываются незначимыми.

Для устранения или уменьшения мультиколлинеарности используется ряд методов.

Самый простой из них – исключение одной или нескольких переменных. При этом, какую переменную оставить, а какую удалить из анализа, решают в первую очередь на основании содержательных соображений. Если с экономической точки зрения ни одной из переменных нельзя отдать предпочтение, то оставляют ту из двух переменных, которая имеет больший коэффициент корреляции с зависимой переменной.

Другой метод устранения или уменьшения мультиколлинеарности заключается в переходе от несмещённых оценок, определённых по методу наименьших квадратов, к смещённым оценкам, обладающим, однако, меньшим рассеянием относительно оцениваемого параметра. Например, при использовании «ридж-регрессии» (или «гребневой регрессии») добавление τ (τ – некоторое положительное число, называемое «гребнем» или «хребтом») к диагональным элементам матрицы X`X делает оценки параметров модели смещёнными, но при этом увеличивается определитель матрицы системы нормальных уравнений. Таким образом, становится возможным исключение мультиколлинеарности в случае, когда определитель |X`X| близок к нулю.

Для устранения мультиколлинеарности может быть использован переход от исходных объясняющих переменных X1, X2,…, Xn, связанных между собой достаточно тесной корреляционной зависимостью, к новым переменным, представляющим линейные комбинации исходных. В качестве таких переменных берут, например, так называемые главные компоненты вектора исходных объясняющих переменных и рассматривают регрессию на главных компонентах, в которой последние выступают в качестве обобщённых объясняющих переменных, подлежащих в дальнейшем содержательной (экономической) интерпретации.

Можно применить преобразование мультиколлинеарных переменных:

– использовать нелинейные формы;

– использовать агрегаты (линейные комбинации нескольких переменных);

– использовать первые разности вместо самих переменных.

Рассмотрим конкретный набор данных и поставим задачу определения совокупности экзогенных переменных, наиболее подходящих для регрессионного анализа.

В качестве исходных данных будем использовать основные показатели баланса компаний-эмитентов, относящихся к сфере деятельности «Связь»[1] (всего 122 компании). Анализу показателей этой отрасли посвящены работы [8], [10].

В качестве результирующей (эндогенной) переменной выбираем показатель чистая прибыль (убыток) компаний.

В силу неоднородности объектов (компаний) была проведена их классификация на однородные группы методами кластерного анализа [2], [5]. В результате получены три кластера со следующими профилями (Кластерные профили – это, по сути, средние значения группирующих переменных в кластере):

1. Первый кластер самый большой – 109 компаний. Среди них много убыточных. Все показатели баланса предприятий этой группы на несколько порядков ниже, чем у других.

2. Второй кластер – 10 крупных прибыльных компаний.

3. Третий кластер – наименьший по количеству компаний, их всего три – Вымпел-Коммуникации (Билайн), Мобильные ТелеСистемы (МТС), Мегафон, но это самые крупные и самые прибыльные компании.

Объективную картину количественных взаимосвязей финансовых показателей предприятий данной отрасли можно получить, используя данные только о компаниях самого крупного первого кластера.

Краткая экономическая характеристика этих показателей:

– валюта баланса (ВБ) – это итог по всем счетам бухгалтерского баланса, сумма всех активов или всех пассивов компании;

– выручка (нетто) от продаж (ВП), дебиторская задолженность (краткосрочная) (ДЗ), запасы готовой продукции и товаров для перепродажи (ЗП), оборотные активы (ОА), основные средства (ОС), прибыль (убыток) от продаж (ПП), чистая прибыль (убыток) (ЧП) – это представители группы активов компании (здесь присутствуют как оборотные, так и внеоборотные активы);

– долгосрочные обязательства (ДО), краткосрочные обязательства (КО) – представители группы пассивов.

Схема отбора экзогенных факторов при решении данной задачи будет выглядеть следующим образом:

I. Корреляционный анализ данных, включая проверку теста Фаррара-Глоубера на мультиколлинеарность факторов;

II. Пошаговый отбор факторов методом исключения из модели статистически незначимых переменных;

III. При несоответствии результатов, полученных в пунктах 1) и 2), проверка теста на «длинную» и «короткую» регрессию.

I. Корреляционный анализ данных, включая проверку теста Фаррара-Глоубера [11] на мультиколлинеарность факторов

В табл. 1 представлена матрица коэффициентов парной корреляции для всех переменных, участвующих в рассмотрении.

Источник

Глава 3. Множественная корреляция и регрессия

Тесты

1. При анализе матрицы парных коэффициентов корреляции получили, что p-value для равна 0,15. Это означает, что:

а) переменная х₂ слабо влияет на изменение у;

б) переменные х₂ и у независимы;

в) переменную х₂ следует включить в регрессию:

г) переменную х₂ не следует включать в регрессию.

При p-value для равном 0,15, принимается гипотеза Н₀, о том что, что коэффициент корреляции между y и x₂ не значимо отличен от нуля, Это означает, что соответствующая независимая переменная не значимо влияет на зависимую переменную, т. е. незначима, и в уравнение регрессии ее включать не следует. Следовательно, правильными являются варианты ответов б) и г).

2. Мультиколлинеарность нежелательна при проведении регрессионного анализа потому, что:

а) вызывает автокорреляцию в остатках;

б) искажает смысл коэффициентов регрессии;

в) нарушает предпосылки МНК;

г) нарушает гомоскедастичность остатков.

В случае же существования взаимозависимости объясняющих переменных смысл коэффициентов уравнения регрессии искажается. А в случае мультиколлинеарности коэффициенты уравнения регрессии вообще теряют какой-либо смысл (о чем речь ниже). Следовательно, правильным является вариант ответа б).

3. Коэффициенты частной корреляции позволяют:

а) выявить связь между одной и многими переменными;

б) выявить парную связь между переменными;

в) выявить чистую связь между переменными;

г) элиминировать наведенные связи между переменными.

Правильным является вариант ответа в), потому что частные коэффициенты корреляции служат показателями чистой линейной корреляционной связи между двумя переменными с исключением влияния других переменных.

4. Коэффициенты множественной корреляции позволяют:

а) выявить связь между одной и многими переменными;

б) выявить парную связь между переменными;

в) выявить чистую связь между переменными;

г) элиминировать наведенные связи между переменными.

Правильным является вариант ответа а), потому что коэффициент множественной корреляции характеризует тесноту связи рассматриваемого набора факторов с результативным признаком, т.е. оценивает тесноту связи совместного влияния факторов на результат.

5. При нарушении предпосылки МНК о нормальном законе распределения остатков

а) оценки параметров уравнения регрессии будут смещенными;

б) оценки параметров уравнения регрессии будут не эффективными;

в) возникнут проблемы при оценке точности уравнения регрессии и его коэффициентов;

г) исказится смысл коэффициентов регрессии.

6. Коэффициенты уравнения регрессии показывают меру влияния факторных переменных (с разными единицами измерения) на результативную, если:

а) уравнение составлено в натуральном масштабе;

б) уравнение составлено в стандартизованном виде;

г) в уравнении отсутствует свободный член;

д) факторные переменные независимы.

Коэффициенты уравнения множественной регрессии при каждой переменной показывают, насколько в среднем изменится значение зависимой переменной (в своих единицах измерения), если значение соответствующей независимой переменной изменится на единицу (в своих единицах измерения) при фиксированных значениях других переменных. Но это верно лишь в том случае, если выполняется основная предпосылка регрессионного анализа, – факторные переменные не зависят между собой (только в этом случае можно изменить значение одной переменной, оставив без изменения другие). В случае же существования взаимозависимости объясняющий переменных смысл коэффициентов уравнения регрессии искажается. А в случае мультиколлинеарности коэффициенты уравнения регрессии вообще теряют какой-либо смысл (о чем речь ниже).

Поэтому, если в условии теста речь идет о величине абсолютного воздействия факторов на результат, то правильными являются варианты ответов а) и д).

b-коэффициенты уравнения регрессии в стандартизованном масштабе создают реальное представление о воздействии независимых переменных на моделируемый показатель. Если величина b-коэффициента для какой-либо переменной превышает значение соответствующего b-коэффициента для другой переменной, то влияние первой переменной на изменение результативного показателя следует признать более существенным.

Поэтому, если в условии теста речь идет о сравнительной величине воздействия факторов на результат, то правильными являются варианты ответов б) и д).

7. Автокорреляция в остатках наблюдается, если

а) неверна спецификация уравнения регрессии;

б) в уравнение регрессии включены незначимые переменные;

в) независимые переменные мультиколлинеарны;

г) в уравнении регрессии отсутствует значимая переменная.

Основными причинами возникновения автокорреляции остатков являются следующие:

— в регрессионную модель не введен значимый факторный признак, и его изменение приводит к значимому изменению остаточных величин;

— в регрессионную модель не включено несколько незначимых факторов, но их изменения совпадают по направлению и фазе, и их суммарное воздействие приводит к значимому изменению остатков;

— неверно выбран вид конкретной зависимости между анализируемыми переменными;

— автокорреляция остатков может возникнуть не в результате ошибок, допущенных при построении регрессионной модели, а вследствие особенностей внутренней структуры случайных компонент (например, при описании динамических рядов регрессией).

Поэтому правильными являются варианты ответов а) и г).

8. существенно меньше . Это значит:

а) уравнение регрессии незначимо;

б) оценки параметров уравнения регрессии неэффективны;

в) уравнение регрессии “засорено” незначимыми переменными;

г) в уравнение регрессии не включена незначимая переменная.

Правильным является вариант ответа в), потому что, при заданном объеме наблюдений при прочих равных условиях с увеличением числа независимых переменных скорректированный коэффициент будет убывать, если в уравнение регрессии будут добавляться незначимые независимые переменные.

9. p-value для статистики Фишера меньше 0,05. Это значит:

а) уравнение регрессии значимо;

б) уравнение регрессии незначимо;

в) все коэффициенты уравнения регрессии равны нулю;

г) не все коэффициенты уравнения регрессии равны нулю.

Если p-value для статистики Фишера меньше 0,05, то принимается гипотеза о значимости уравнения регрессии. В свою очередь, если уравнение регрессии является значимым, то, следовательно, в модели присутствуют факторы, оказывающие реальное влияние на результативный признак, т.е. не все коэффициенты уравнения регрессии равны нулю.

Поэтому правильными являются варианты ответов а) и г).

10. Коэффициент множественной детерминации показывает

а) на сколько процентов изменится зависимая переменная, если независимая переменная изменится на 1%;

б) долю вариации зависимой переменной, обусловленную вариацией независимых переменных;

в) на какую часть своего стандартного отклонения изменится зависимая переменная, если независимая переменная изменится на величину своего стандартного отклонения;

г) насколько изменится зависимая переменная, если независимая переменная изменится на единицу.

Коэффициент множественной детерминации показывает долю вариации одной (результативной) переменной, обусловленную изменением других, включенных в анализ, переменных, поэтому правильным является вариант ответа б).

Источник

Мультиколлинеарность

Последствия и признаки мультиколлинеарности

К каким трудностям приводит мультиколлинеарность факторов, включенных в модель, и как они могут быть разрешены?

Точных количественных критериев для обнаружения частичной мультиколлинеарности не существует. О наличии мультиколлинеарности может свидетельствовать близость к нулю определителя матрицы (X T X). Также исследуют значения парных коэффициентов корреляции. Если же определитель матрицы межфакторной корреляции близок к единице, то мультколлинеарности нет.

С помощью какой меры невозможно избавиться от мультиколлинеарности?
a) увеличение объема выборки;
b) исключения переменных высококоррелированных с остальными;
c) изменение спецификации модели;
d) преобразование случайной составляющей.

Парные (линейные) и частные коэффициенты корреляции

Парный коэффициент корреляции изменяется в пределах от –1 до +1. Чем ближе он по абсолютной величине к единице, тем ближе статистическая зависимость между x и y к линейной функциональной. Положительное значение коэффициента свидетельствует о том, что связь между признаками прямая (с ростом x увеличивается значение y ), отрицательное значение – связь обратная (с ростом x значение y уменьшается).
Можно дать следующую качественную интерпретацию возможных значений коэффициента корреляции: если |r| 0.7, то в данной модели множественной регрессии существует мультиколлинеарность.
Поскольку исходные данные, по которым устанавливается взаимосвязь признаков, являются выборкой из некой генеральной совокупности, вычисленные по этим данным коэффициенты корреляции будут выборочными, т. е. они лишь оценивают связь. Необходима проверка значимости, которая отвечает на вопрос: случайны или нет полученные результаты расчетов.
Значимость парных коэффициентов корреляции проверяют по t-критерию Стьюдента. Выдвигается гипотеза о равенстве нулю генерального коэффициента корреляции: H₀: ρ = 0. Затем задаются параметры: уровень значимости α и число степеней свободы v = n-2. Используя эти параметры, по таблице критических точек распределения Стьюдента находят t_кр, а по имеющимся данным вычисляют наблюдаемое значение критерия:
, (2)
где r – парный коэффициент корреляции, рассчитанный по отобранным для исследования данным. Парный коэффициент корреляции считается значимым (гипотеза о равенстве коэффициента нулю отвергается) с доверительной вероятностью γ = 1- α, если t_Набл по модулю будет больше, чем t_крит.
Если переменные коррелируют друг с другом, то на значении коэффициента корреляции частично сказывается влияние других переменных.

Пошаговая регрессия

На втором шаге строится уравнение регрессии с одной переменной, имеющей максимальный по абсолютной величине парный коэффициент корреляции с результативным признаком.

На третьем шаге в модель вводится новая переменная, имеющая наибольшее по абсолютной величине значение частного коэффициента корреляции с зависимой переменной при фиксированном влиянии ранее введенной переменной.
При введении в модель дополнительного фактора коэффициент детерминации должен возрастать, а остаточная дисперсия уменьшаться. Если этого не происходит, т. е. коэффициент множественной детерминации увеличивается незначительно, то ввод нового фактора признается нецелесообразным.

Источник

Проблема мультиколлинеарности

Мультиколлинеарность – это линейная зависимость между двумя или несколькими факторными переменными в уравнении множественной регрессии. Если такая зависимость является функциональной, то говорят о полной мультиколлинеарности. Если же она является корреляционной, то имеет место частичная мультиколлинеарность. Если полная мультиколлинеарность является скорее теоретической абстракцией (она проявляется, в частности, если фиктивную переменнную, имеющую k уровней качества, заменить на k дихотомических переменных), то частичная мультиколлинеарность весьма реальна и присутствует практически всегда. Речь может идти лишь о степени ее выраженности. Например, если в состав объясняющих переменных входят располагаемый доход и потребление, то обе эти переменные, конечно, будут сильно коррелированными.

Отсутствие мультиколлинеарности является одной из желательных предпосылок классической линейной множественной модели. Это связано со следующими соображениями:

1) В случае полной мультиколинеарности вообще невозможно построить оценки параметров линейной множественной регрессии с помощью МНК.

2) В случае частичной мультиколлинеарности оценки параметров регрессии могут быть ненадежными и, кроме того, затруднено определение

изолированного вклада факторов в результативный показатель.

Главной причиной возникновения мультиколлинеарности является наличие в изучаемом объекте процессов, которые одновременно влияют на некоторые входные переменные, но не учтены в модели. Это может быть результатом некачественного исследования предметной области или сложности взаимосвязей параметров изучаемого объекта.

Подозрением наличия мультиколлинеарности служат:

– большое количество незначимых факторов в модели;

– большие стандартные ошибки параметров регрессии;

– неустойчивость оценок (небольшое изменение исходных данных приводит к их существенному изменению).

Один из подходов для определения наличия или отсутствия мультиколлинеарности заключается в анализе корреляционной матрицы

между объясняющими переменными 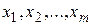и выявлении пар факторов, имеющих высокие коэффициенты парной корреляции (обычно больше 0,7). Если такие факторы существуют, то говорят о явной коллинеарности между ними.

Однако парные коэффициенты корреляции, рассматриваемые индивидуально, не могут оценить совокупное взаимодействие нескольких факторов (а не только двух).

Поэтому для оценки наличия мультиколлинеарности в модели используется определитель матрицы парных коэффициентов корреляции между факторами (определитель матрицы межфакторной корреляции)

.

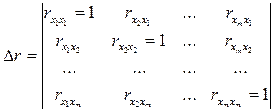
Чем ближе определитель матрицы межфакторной корреляции к 0, тем сильнее мультиколлинеарность, и наоборот, чем ближе определитель к 1, тем меньше мультиколлинеарность.

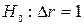
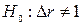
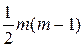
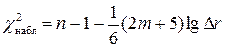
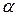
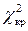
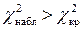
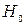
Статистическая значимость мультиколлинеарности факторов определяется проверкой нулевой гипотезы при альтернативной гипотезе . Для проверки нулевой гипотезы используется распределение Пирсона с степенями свободы. Наблюдаемое значение статистики находится по формуле , где n – число наблюдений, m – число факторов. Для заданного уровня значимости по таблице критических точек распределения Пирсона определяется критическое значение . Если , то гипотеза отклоняется и считается, что в модели присутствует мультиколлинеарность факторов.

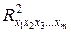
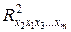
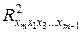
Выделить факторы, влияющие на мультиколлинеарность, позволяет также анализ коэффициентов множественной детерминации, вычисленных при условии, что каждый из факторов рассматривается в качестве зависимой переменной от других факторов: , , …, . Чем ближе они к 1, тем сильнее мультиколлинеарность факторов. Значит, в уравнении следует оставлять факторы с минимальной величиной коэффициента множественной детерминации.

Что касается полной мультиколлинеарности, то с ней следует вести самую решительную борьбу: сразу же удалять из регрессионного уравнения переменные, которые являются линейными комбинациями другихпеременных.

Частичная мультиколлинеарность не является таким уж серьезным злом, чтобы ее выявлять и устранять. Все зависит от целей исследования. Если основная задача моделирования – только прогнозирование значений зависимой переменной, то при достаточно большом коэффициенте детерминации ( 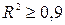) присутствие мультиколлинеарности не сказывается на прогнозных качествах модели. Если же целью моделирования является и определение вклада каждого фактора в изменение зависимой переменной, то наличие мультиколлинеарности является серьезной проблемой.

Простейшим методом устранения мультиколлинеарности является исключение из модели одной или ряда коррелированных переменных.

Поскольку мультиколлинеарность напрямую зависит от выборки, то, возможно, при другой выборке мультиколлинеарности не будет вообще либо она не будет настолько серьезной. Поэтому для уменьшения мультиколлинеарности в ряде случаев достаточно увеличить объем выборки.

Иногда проблема мультиколлинеарности может быть решена путем изменения спецификации модели: либо изменяется форма модели, либо добавляются факторы, не учтенные в первоначальной модели, но существенно влияющие на зависимую переменную.

В ряде случаев минимизировать либо совсем устранить мультиколлинеарность можно с помощью преобразования факторных переменных. При этом наиболее распространены следующие преобразования:

1. Линейная комбинация мультиколлинеарных переменных (например, ).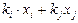

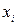
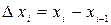
2. Замена мультиколлинеарной переменной ее приращением .

3. Деление одной коллинеарной переменной на другую.

Источник