градус делится на что

Градусная мера угла

Градус — угол, равный 1/180 части развернутого угла. Градусная мера
угла — это положительное число, показывающее сколько раз градус и его части
укладываются в данном угле. Углы измеряют с помощью транспортира.

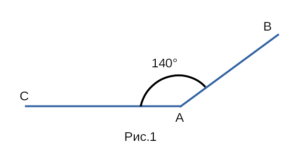
На рисунке 1 изображен ∠СAB. Градусная мера
которого равна 140°. Обычно записывают кратко: ∠СAB=140°.

Названия определённых частей градуса:

Минута — это 1/60 часть градуса. Секунда — это 1/60 часть минуты.
Минуту обозначают знаком ′, а секунду знаком ″.
Например, угол 45 градусов, 30 минут, 15 секунд обозначают вот так: 45°30′15″.

Равные углы имеют равные градусные меры. Меньший угол имеет меньшую градусную меру.

Мы знаем, что градус составляет 1/180 часть развернутого угла, из этого мы можем сделать вывод, что
развернутый угол равен 180°. Мы также знаем, что неразвернутый угол меньше развернутого угла,
поэтому неразвернутый угол меньше 180 градусов.

Когда луч делит угол на два угла, градусная мера всего угла равна сумме градусных мер этих углов.
Пример на рисунке 2 — ∠CAH + ∠BAH = ∠CAB ⇒ 60° + 120° = 180°.

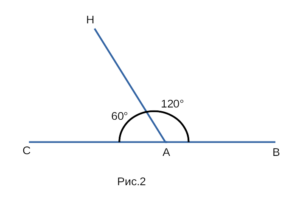
Углы называют не только развернутыми и неразвернутыми, но и еще называют
прямыми, острыми и тупыми. Прямым называется угол равный 90°. Острым называется
угол меньше 90°. Тупым называется угол больше 90°, но меньше 180°.

Источник

Углы. Градусная мера угла.

Мерой угла является размер поворота луча около точки как центра вращения.

Что такое градусная мера угла? Градусной мерой угла является число больше нуля, которое показывает,

величина, которая отражает число градусов, минут и секунд между двумя сторонами угла.

У любого угла существует определенная градусная мера, которая больше 0. Развернутый угол = 180°.

Градусная мера угла соответствует сумме градусных мер углов, разбиваемый всяким лучом, который

проходит между его сторонами.

От всякого луча в необходимую полуплоскость есть возможность отложить угол с необходимой градусной

мерой, меньше чем 180°, и только 1.

Мерой плоского угла, который является элементом полуплоскости, является градусная мера угла с теми же

где α – градусная мера дополнительного плоского угла.

2 угла будут называться равными, когда их градусные меры одинаковы.

Свойства углов.

который проходит меж его сторонами.

мерой, меньше чем 180°, и только один.

Как найти градусную меру угла?

1 градус (°) — это угол, равный 1/180 части развернутого угла. Если выразиться по другому, если возьмем

развернутый угол и поделим его на 180 одинаковых меж собой частей-углов, то любой такой маленький угол

будет соответствовать 1 градусу. Размер остальных углов вычисляется тем, какой число этих маленьких

углов возможно разместить внутри угла, который измеряется.

Т.о., развернутый угол = 180°, прямой угол = 90°, острые углы меньше, чем 90°, а тупые — больше,

Если угол невозможно измерить точно в целых градусах, то не обязательно использовать минуты и секунды.

Можно пользоваться дробными значениями градуса. Например, 96,5°.

Известно, что минуты и секунды легко переводятся в градусы, выражая их в долях градуса.

Например, 30′ = (30/60)° или 0,5°. А 0,3° = (0,3 * 60)’ или 18′. Т.о., пользоваться минутами и секундами —

Источник

Углы и градусы

Определение величин углов

Первые попытки древних людей измерять земельные участки
(изначально геометрия – это измерение земли) наткнулись на
острую необходимость в угловых измерениях. Крайне редко
их наделы имели правильную форму. Поэтому понятие угла
появилось практически одновременно с линейным отрезком
и/или расстоянием. Другое дело, измерять и тем более
вычислять значения углов люди научились значительно позже.
Хотя уже древние греки оперировали этими понятиями более чем успешно.

Полупрямая (луч) в геометрии определяется как бесконечно длинная
прямая, имеющая начало. Она состоит из всего множества точек,
лежащих на этой линии, включая начальную. Угол же образуют два
луча с совмещенными точками начала. Можно дать и такое
определение этой геометрической фигуры. Причем общую для лучей
точку принято называть вершиной угла, а лучи – сторонами угла.

Удивительно, но размещение точки в любом месте любой прямой
эквивалентно получению двух равновеликих и разнонаправленных
лучей с общим началом. Следовательно, эта нехитрая операция
создает угол как геометрическую фигуру.

Откуда взялся градус

Достоверное происхождение этой угловой меры неизвестно.
Наиболее вероятная гипотеза о делении на 60 частей
угла равностороннего треугольника вавилонянами отлично
согласуется с шести десятеричной системой счисления, принятой
в этом архаичном обществе. Число 60 делится на 2, 3, 5, 6, 10,
15, 30 и, собственно, на 60. Отсюда удобство его применения в
торговле и прочих бытовых отношениях.

Согласно другой версии, окружность разделили на 360 равных
фрагментов по причине равенства их количества числу дней в году.
Персы, например, немало повлиявшие на развитие математики в
целом и геометрии в частности, использовали именно такой календарь.

В любом случае градус используется до сих пор, обозначая 1/360 часть
полного оборота (делит круг на 360 равных секторов). Само слово с
латыни переводится как шаг, ступень, порог. Отсюда слово градуировка,
применимое абсолютно ко всем измерительным приборам.

Для измерения более мелких величин углов используют минуту
и секунду. Эти величины также являются результатом дробления
на 60. Минута делит градус, а секунда минуту. То есть 1 минута
равна 1/60 градуса, а секунда составляет 1/60 минуты или 1/3600 градуса.

Транспортир, знакомый каждому со школьных времен – элементарнейший
инструмент, позволяющий довольно точно измерять или рисовать углы.
Разумеется, в практике промышленности, строительства и других сферах
человеческой деятельности применяются более точные средства,
теодолит, как вариант. Но результат измерения любого современного
инструмента всегда выражается в градусах.

Учитывая простоту фигуры и ее составляющих, углы не отличаются
большим разнообразием. Принято выделять следующие их виды:

Помимо прямого, существует еще несколько частных случаев, а именно:

Геометрия, оставаясь неотъемлемой частью математики,
все же выделена в отдельную дисциплину. Причина
такого подразделения проста. Математическая наука
не терпит даже тени хаоса, что выражается в четкой
классификации ее разделов, но с сохранением
органической связи между собой.

На самом деле, без глубокого знания основ геометрии
практически невозможно изучить смежные математические
дисциплины, такие как тригонометрия, анализ, интегральное
или дифференциальное счисления. Более того, изучение
любой точной науки требует свободного владения
геометрическими понятиями. Механика или оптика
в физике – наиболее яркое тому подтверждение.

Источник

ГРАДУС

Полезное

Смотреть что такое «ГРАДУС» в других словарях:

ГРАДУС — (лат. gradus степень, ступень, мера). 1) одна из равных частей, на которые делится окружность (обыкновенно 1/360 часть). В физике: каждая из равных частей, на которые делится шкала термометра, барометра и др. приборов. 3) в древн. Руси: ученая… … Словарь иностранных слов русского языка

ГРАДУС — (лат. gradus шаг ступень, степень), 1) общее наименование различных единиц температуры, соответствующих разным температурным шкалам. Различают градус шкалы Кельвина, или кельвин (К), градус Цельсия (.С), градусы Реомюра (.R), Фаренгейта (.F). 1К … Большой Энциклопедический словарь

градус — ступень (Даль) См. степень. Словарь русских синонимов и сходных по смыслу выражений. под. ред. Н. Абрамова, М.: Русские словари, 1999. градус высота, степень, ступень; лигрил, десцендент, крепость, мера Словарь русских синоним … Словарь синонимов

ГРАДУС — муж. степень, ступень. Окружность круга делится на 360 градусов, которые и служат мерою для дуги, определяя, какую часть окружности она составляет, и мерою для углов, измеряемых дугою. Градус великого круга земли содержит около 105 верст или 60… … Толковый словарь Даля

ГРАДУС — (от латинского gradus шаг, ступень, степень), 1) общее наименование различных единиц температуры, соответствующих разным температурным шкалам. Различают градусные шкалы Кельвина, или кельвин (К), градус Цельсия (шC), градусы Реомюра (шR),… … Современная энциклопедия

ГРАДУС — ГРАДУС, в математике единица угловой меры, равная одной тристашестидесятой (1/360) части полного круга (360°). Один градус записывается как 1°, он подразделяется на 60 частей, называемых минутами («дуговыми минутами»), которые обозначаются как 1… … Научно-технический энциклопедический словарь

ГРАДУС — ГРАДУС, градуса, муж. (лат. gradus ступень, шаг) (научн.; условно обозначается вверху цифры справа маленьким кружком). 1. Единица измерения дуг и углов, равная 1/360 окружности. Угол в 45 градусов или в 45°. Градус широты. 2. Деление на шкале… … Толковый словарь Ушакова

ГРАДУС — (от лат. gradus шаг, ступень, степень) температурный, общее наименование разл. ед. темп ры, соответствующих разным температурным шкалам. Различают Г. шкалы Кельвина, или кельвин (К), градус Цельсия (°С), Реомюра (°R), Фаренгейта (°F), Ранкина… … Физическая энциклопедия

ГРАДУС — (Degree) 1. Единица измерения угла или дуги, равная 1/90 прямого угла или 1/360 окружности (см. Угол). Применяется для измерения углов, дуг, меридианов, параллелей, широт, долгот, азимутов и т. д. Угол в 1° образуется двумя радиусами,… … Морской словарь

градус — degree Grad 1).Одиниця виміру температури. Розрізняють Г. шкали Кельвіна (К), Цельсія (ОС), Реомюра (ОR), Фаренгейта (ОF). 1 К = 1 ОС = 0,8 ОR = 1,8 ОF. 2). Позасистемна одиниця вимірювання плоского кута, яка допущена міжнародним стандартом для… … Гірничий енциклопедичний словник

Источник

Измерение углов: градусы и радианы

Для измерения углов принято использовать две основные единицы: градусы и радианы.

Начнем с привычных градусов.

Полный круг составляет 360 градусов – это мы все знаем.

А вот в часе 60 минут, в круге 360 градусов. И в сутках 24 часа. Древние шумеры умудрились придумать двенадцатеричную систему счисления! И при этом они тоже считали по пальцам. Нет, у них не было по 6 пальцев на каждой руке. Просто считали не пальцы, а фаланги четырех пальцев (кроме большого).

Кстати, круг легко делится именно на 6 частей (умеете?). А число 12 (дюжина) делится на 2, 3, 4, 6 и, собственно, 12.

И это не все. Древние шумерские астрономы обнаружили, что в день равноденствия Солнце встает почти точно на Востоке и заходит почти точно на Западе, причем от восхода до заката проходит по небу путь, в 360 раз больший, чем видимый с Земли диаметр Солнца. Небесную полуокружность разделили на 180 градусов.

Точнее, угловой диаметр Солнца равен примерно 32 угловых минуты, то есть чуть больше 0,5 градуса. Он еще и немного меняется в течение года из-за того, что орбита Земли не круговая, а эллиптическая.

Так что утверждение о том, что в День равноденствия Солнце проходит по небу путь, равный 360 своим «шагам» (то есть 360 видимым диаметрам солнца) – верно с некоторой точностью.
Конечно, древние астрономы наблюдали не только за движением Солнца. Они заметили, что яркая планета Юпитер совершает полный оборот вокруг Солнца за 12 лет. Точнее, не 12, а 11,86 лет, но уж очень им хотелось округлить до своего любимого числа.

Да что там Юпитер! Посмотрим на Луну. Юпитер на небе еще и не каждый найдет (а вы сможете?) – зато Луну, особенно полную, трудно не заметить! Месяц – промежуток от полнолуния до полнолуния – равен примерно 29,5 суток. Почти 30, верно?

Наша Земля совершает полный оборот вокруг Солнца за 365 дней (точнее, за 365,242 суток), и это – солнечный год.

И тогда лунный год – это 12 месяцев, в каждом месяце 30 дней (округлили), вот и получается 360 дней в году, почти столько же, сколько в солнечном, в котором 365 дней.

«Может быть, боги хотели сделать в году ровно 360 дней, но им кто-нибудь помешал, вот и получилось 365». Возможно, так и рассуждали древние астрономы, деля круг на 360 частей, 360 градусов. Тем более, что 360 – число, имеющее целых 24 делителя.

Число 360 делится на 1, 2, 3, 4, 5, 6, 8, 9, 10, 12, 15, 18, 20, 24, 30, 36, 40, 45, 60, 72, 90, 120, 180 и 360. Очень удобно делить 360 градусов на части!

Обозначается: 360°. Этот кружок вверху – специальный символ для обозначения градуса.

Есть и другая мера измерения углов – радианная.

1 радиан – центральный угол, опирающийся на дугу, равную радиусу окружности.

Как перевести градусы в радианы и наоборот?

Составим пропорцию. Длина окружности так относится к длине дуги на нашем рисунке, как – к величине угла, опирающегося на эту дугу, то есть к углу в 1 радиан.

Слева в нашей пропорции углы, справа – длина полной окружности и длина отмеченной на рисунке дуги.

Из этой пропорции получаем, что радиан. Значит, полный круг – это радиан. Тогда полкруга – это радиан, четверть круга (то есть ) – это радиан.

Любой угол, выраженный в градусах, можно перевести в радианы. И наоборот, 1 радиан приблизительно равен 57 градусам.

Источник