гравитационный скачок что это
Гравицапа для межпланетных перелётов или гравитационный манёвр
Вопрос эмиграции в последние десятилетия стоит наиболее остро. И если 40 лет назад пределом мечтаний было перебраться за океан, то в XXI веке умами овладела мечта о релокейшне на Марс, например. Однако там тоже в скором времени может стать тесно. Остаётся одна дорога — колонизация Солнечной Системы и экзопланет. Допустим, мы собрались покинуть внутреннюю область Солнечной Системы, а, если повезёт, то и совсем выбраться за её пределы. Помимо невероятных объёмов тушёнки и кислорода, необходимых для выживания в суровом Космосе, нам потребуется в разы на порядки большее количество топлива, чтобы всё это добро дотащить. И ещё столько же топлива, чтобы тащить то топливо. И ещё топливо.
И самое обидное, что скорее всего мы закончим свой век среди троянских астероидов Юпитера, померев от тоски. Потому что топлива всё равно ни на что не хватит. Однако присмотримся к нашей Солнечной системе повнимательнее. Вот те же «троянцы и греки» — не просто так столпились в точках Лагранжа L4 и L5 Юпитера. Их туда «затолкала» гравитация планеты-гиганта, не потратив ни единой капли гидразина.
Давайте же и мы применим дармовую энергию Природы для достижения благородной цели доставки полезной нагрузки в далёкий космос.

Юпитер — оранжевый, «Троянцы» — зелёные за ним, «греки» — зелёные перед ним
Как это работает
Идея использования гравитации пролетающей мимо планеты довольно проста. Все что нужно — это наличие вблизи трассы полета небесного тела, обладающего достаточно сильной гравитацией и подходящими для целей миссии положением и скоростью. Космический аппарат, попав в поле тяготения планеты обязательно изменит свою скорость. Здесь внимательный читатель может заметить, что аппарат, ускорившись гравитацией планеты, ею же и тормозится после сближения с небесным телом и что в результате никакого ускорения не будет. Действительно, скорость относительно планеты, используемой в качестве «гравитационной пращи», не изменится по модулю. Но она поменяет направление! А в гелиоцентрической (связанной с Солнцем) системе отсчета окажется, что скорость меняется не только по направлению, но и по величине, поскольку складывается из скорости аппарата относительно планеты и, по крайней мере частично, скорости самой планеты относительно Солнца. Бинго! Планеты будут «брать на буксир» наших путешественников.
Подобным способом можно без затрат топлива изменить кинетическую энергию межпланетной станции. При полетах к дальним, внешним, планетам Солнечной системы гравитационный манёвр используется для разгона (для этого траектория корабля должна пролегать «за» планетой, или как говорят, с внешней стороны орбиты):
… а при миссиях к внутренним планетам — напротив, для гашения гелиоцентрической скорости (тут, соответственно, пролетаем «перед» планетой):
Упрощая, можно сказать, что сближение аппарата с планетой с внутренней стороны ее орбиты приводит к тому, что аппарат отдает планете часть своего углового момента и замедляется; и наоборот, сближение с внешней стороны орбиты приводит к увеличению момента и скорости аппарата. Интересно, что никакими акселерометрами на борту зарегистрировать изменение скорости аппарата в маневрах невозможно, — они постоянно регистрируют состояние невесомости. Сила притяжения планеты уравновешивает центробежную силу, когда мы закладываем такой поворот.
Причём экономия топлива, достигаемая использованием волшебной силы гравитации колоссальная. Первая космическая скорость — 8 км/с обеспечивает нам вращение вокруг Земли. Для перехода на более высокую орбиту скорость надо увеличивать, и каждые 3 км/с дополнительного разгона втрое увеличивают стартовую массу космической ракеты. Чтобы с низкой околоземной орбиты (скорость 8 км/с) отправиться на марсианскую по эллиптической («гомановской») траектории, надо набрать около 3,5 км/с, к Юпитеру — 6 км/с, к Плутону — 8—9 км/с. Таким образом полезная нагрузка при полете к дальним планетам составляет лишь несколько процентов от выведенной на орбиту массы, а та, в свою очередь, лишь несколько процентов стартовой массы ракеты. А вот какой максимальный прирост скорости может дать нам гравитация планет:
Меркурий: 3,005 км/с
Венера: 7,328 км/с
Земля (надо же): 7,910 км/с
Луна (тоже мне планета): 1,680 км/с
Марс: 3,555 км/с
Юпитер: 42,73 км/с
Сатурн: 25,62 км/с
Уран: 15,18 км/с
Нептун: 16,73
Плутон (уже не планета, но всё же): 1,09
Если присмотреться, данные теоретические пределы приращения скорости примерно равны первой космической скорости для этих планет. При этом ваш трактор космический аппарат отклонится на 60 градусов от первоначальной траектории.
Может показаться, что топливо при подобных путешествиях вообще не нужно, но это, разумеется, не так. Во-первых, до ближайшего гравитирующего тела надо ещё долететь. Причём желательно долететь до Юпитера. Впрочем, для полётов к Юпитеру есть свои лайфхаки, о которых ниже. Во-вторых, далеко не всегда направление полёта после ускорения планетой нас устраивает, поэтому траекторию нужно корректирвать двигателями. Кстати это делать лучше в моменты, когда скорость минимальна — то есть ещё до входа в вираж, предварительно просчитав конус траекторий наперёд. Ну и в-третьих, в момент максимального действия гравитационной пращи, находясь в ближайшей окрестности планеты и обладая пиковой скоростью хорошо бы как следует подработать маршевым двигателем. При движении с высокой скоростью топливо имеет больше энергии, доступной для использования за счёт эффекта Оберта (причём при скорости, превышающей половину скорости реактивной струи, полученная кинетическая энергия может превысить потенциальную химическую энергию сгораемого топлива — радуйтесь, торсионщики!)
Хватит болтать — в дорогу!
Ракета с модулем Пионер 10 стартовала 3 марта 1972 года с базы ВВС США на мысе Канаверал носителем Атлас-Центавр. Гравитационный маневр вокруг Юпитера позволил станции превысить третью космическую скорость, достаточную для того, чтобы навсегда покинуть Солнечную систему. Пересечь орбиту Сатурна «Пионер-10» смог к февралю 1976 года, в июле 1979 года оказался за орбитой Урана, в 1983 году первым в истории пересек орбиту Нептуна. Последние данные от станции получены 23 января 2003 года, после чего «Пионер-10» прекратил свою работу. Сейчас аппарат находится на расстоянии 120 астрономических единиц от Солнца и через пару миллионов лет наконец-то приблизится к звезде Альдебаран.
Однако первый гравитационный манёвр совершила советская станция Луна-3 в 1959 году для того, чтобы вернуться обратно. Ну ладно, такой себе вираж, — зато это был манёвр с изменением плоскости траектории полёта. Подобные полёты и сегодня совершаются только при помощи гравитационной пращи. Например, аппарат для исследования полярных областей Солнца «Улисс» был вынужден «давать крюк» мимо Юпитера. Стартовав в 1990, он в 1992 году подлетел к газовому гиганту на расстояние 6 его радиусов и в 1994 году уже созерцал южный полюс Солнца с безопасного расстояния. Тут можете посмотреть на анимацию его полёта (гифка 3 мегабайта).
Американский Маринер 10 в 1974 году, наоборот, совершал торможение «об Венеру» для последующих сближений с Меркурием (весьма и весьма точных — 705 и 318 км!). Этот же метод используется и по сей день для исследования Меркурия — например, в миссиях «MESSENGER» и «БепиКоломбо». Тут я положил ссылочку на 8-мегабайтную гифку с анимацией движения последнего модуля за период 2019-2025 годы.
Если до соседней планеты лететь далеко и топлива жалко, можно сделать вот такой финт:
Аппарат миссии Юнона, взлетел с Земли, но с орбиты не сошёл, а произвёл гравитационный манёвр так же с Землёй, после чего направился на орбиту Юпитера. Таким же макаром разгонялся «Galileo Orbiter». Сначала аппарат направился к Венере, мимо которой прошел в феврале 1990 г. Затем по новой траектории в декабре он вернулся к Земле. Были переданы многочисленные фотографии Венеры, Земли и Луны, а наш герой понёсся далее.

7 декабря 1995-го исследовательский аппарат «Галилео» прибыл к Юпитеру и направил к нему исследовательский зонд (синие точки)
Про миссию Кассини-Гюйгенс, посадившую спускаемый аппарат на поверхность спутника Сатурна — Титана, говорить можно не один день. Шутка-ли — 20 лет работы на различных орбитах. Эти 20 лет стали возможны в том числе и благодаря максимально возможному использованию гравитации планет Солнечной Системы для экономии топлива.
Помимо плотной серии пиков в конце графика (когда аппарат вышел на орбиту Сатурна, и начал вращаться на его орбите) отчётливо видны моменты встреч с планетами (во время которых у аппарата прибавляется скорость), плавное снижение скорости (когда аппарат летел на встречу Сатурну, выбираясь из «гравитационной ямы» Солнца) с небольшим изломом у Юпитера.
Легендарный Кассини в общей сложности сделал 293 оборота вокруг Сатурна, среди которых выполнил 162 прохода вблизи его спутников и открыл 7 новых из них.
Разумеется, для выполнения гравитационных маневров дата старта должна быть выдержана весьма точно. Баллистики оперируют понятием «окно запуска» — это интервал дат, в пределах которого эффективность запланированных гравитационных маневров максимальна. Ближе к краям «окна» эффект становится меньше, а потребности в топливе — больше. Если же выйти за его границы, то носитель просто не сможет вывести аппарат на нужную орбиту, что приведет к срыву полета или недопустимому возрастанию его длительности. Например, запуск «Новых горизонтов», добывших нам такие милые фотографии Плутона, неоднократно переносился по погодным и техническим причинам. Задержись старт еще на несколько дней, и зонд отправился бы в полет уже без расчета на «гравитационную помощь» Юпитера и с меньшими шансами на успех.

Прибавка к скорости в 4 км/с позволила добраться до Плутона прежде чем на нём начала замерзать атмосфера (так как планетоид сейчас удаляется от Солнца). Поэтому он тут такой красивый.
«Лестница Лагранжа»
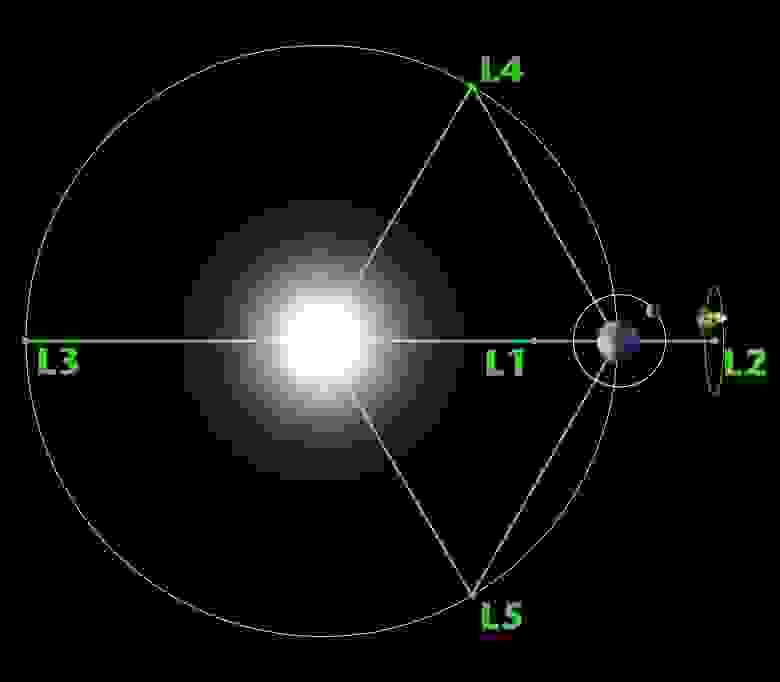
В начале статьи я упомянул о точках Лагранжа на просто так. Они есть у каждой пары космических тел (обычно — Солнца и планеты, но есть и у планет со спутниками) и вблизи них космический аппарат может находиться довольно долго в состоянии неустойчивого равновесия и быть почти неподвижным относительно этой планеты. Например, точки L1 и L2 Земли находятся на оси Земля-Солнце.
На таких орбитах станции будут обращаться вокруг Солнца, оставаясь неподвижными относительно Земли, — в направлении к Солнцу и от него. Это так называемые точки Лагранжа L1 и L2, где космический аппарат может неподвижно висеть, не расходуя топлива. Этим уже давно пользуются: в L1 работает солнечная обсерватория SOHO, а в L2 — астрофизический зонд WMAP. Туда же планируется вывести 6-метровый телескоп имени Джеймса Уэбба, который строится на смену стареющему «Хабблу».
Взгляните на эту непростую траекторию аппарата ISEE-3/ICE:
Труженик ISEE-3/ICE четыре года (1978—1982) изучал Солнце с орбиты вокруг точки Лагранжа L1, а затем путем сложных гравитационных маневров у Земли и Луны он был направлен на встречу с кометами Джакобини — Циннера (1985) и Галлея (1986). В 2012 году он вернулся к нам, но интерес к миссии был уже потерян, и даже оборудование для связи с ним было списано. И в 2014 году связь с ним была окончательно потеряна, ну да ладно.
Среди многочисленных траекторий ухода от точки L1 есть такие, которые на время приводят аппарат на орбиту вокруг L2 (и наоборот). Причем для этого не требуется серьезных затрат топлива. Для случая с нашей планетой это не столь важно. То ли дело — система Юпитера или Сатурна, в которых для каждого большого спутника есть пара таких точек. Например, для Ио, Европы, Ганимеда и Каллисто на орбите Юпитера. Двигаясь вокруг планеты, внутренние спутники обгоняют внешние, и если правильно подгадать, то ценой совсем небольших затрат топлива аппарат может перепрыгнуть с неустойчивой орбиты вокруг точки L2, скажем, спутника Ио на такую же орбиту вокруг точки L1 Европы. Покрутившись там и проведя наблюдения, можно подняться еще на одну ступеньку «лестницы» — к точке L2 Европы, а оттуда в нужный момент прыгнуть к L1 Ганимеда, а там и до Каллисто недалеко. Спускаться по этой «лестнице Лагранжа» тоже не возбраняется.
Именно такой план полета предлагался для большой исследовательской станции JIMO (NASA). Однако эту экспедицию отменили враги, и теперь вместо неё будет миссия JUICE (Jupiter Icy Moons Explorer), которую Европейское Космическое Агентство готовит для изучения галилеевых спутников Юпитера. До сих пор спутники Юпитера исследовались только с пролетных траекторий. «Лестница Лагранжа» позволит станции подолгу зависать над спутником — изучать его поверхность и отслеживать происходящие на ней процессы.
Каковы перспективы? Автостопом до облака Оорта?
В нашей звёздной системе насчитывается несколько десятков крупных и тысячи не очень массивных космических тел. Разумеется, бросается в глаза «великолепная пятёрка»: Солнце, Юпитер, Сатурн, Уран и Нептун. Однако гравитационные возмущения в траектории полётов космических аппаратов вносят все тела Солнечной системы, не забывая возмущать орбиты друг друга. И сейчас мы уже можем позволить рассчитывать гравитационное влияние и малых планет Солнечной систем. Вот, например, миссия Rosetta к комете Чюрюмова-Герасименко (2004-2016 гг). Вначале аппарат двинулся к Солнцу и, обогнув его, вновь вернулся к Земле, откуда двинулся навстречу Марсу. Обогнув Марс, аппарат вновь сблизился с Землёй и затем снова вышел за орбиту Марса. К этому моменту комета находилась за Солнцем и ближе к нему, чем Rosetta. Новое сближение с Землёй направило аппарат в направлении кометы, которая в этот момент направлялась от Солнца вовне Солнечной системы. В конце концов Rosetta сблизилась с кометой с требуемой скоростью. Столь сложная траектория позволила снизить расход топлива за счёт использования гравитационных полей Солнца, Земли и Марса. Тут гифка с полным маршрутом аппарата.
А вот выход на орбиту кометы в целях её исследования и отправки на её поверхность спускаемого аппарата «Филы»:
Расчёт баллистических траекторий это «не решаемая» в лоб задача многих тел, требующая колоссальных вычислительных мощностей для совершения достаточного числа итераций. Но вот неуклонный рост этих самых вычислительных мощностей позволяет учитывать влияние всё большего числа массивных объектов, переводя это влияние из разряда неизбежной погрешности вычислений в разряд заранее предсказанных. Таким образом число «окон запуска» только растёт.
Вот тут, например, в очередной раз сообщается об обнаружении «скоростного хайвея» в Солнечной Системе — сложного переплетения гравитационных возмущений от тел Солнечной Системы, позволяющих точнее рассчитать траектории аппаратов и использовать ещё больше гравитационных манёвров вместо траты драгоценного топлива.
Постепенно расчёты полётов по нашей планетной системе будут становиться похожими больше на автобусное расписание нежели на ожидание у моря погоды. Точность небесной механики, помноженная на точность наблюдений и вычислений, способна совершить переворот в наших взглядах на космические путешествия.
Облачные серверы от Маклауд идеально подходят для расчета траектории вашего побега на Марс.
Зарегистрируйтесь по ссылке выше или кликнув на баннер и получите 10% скидку на первый месяц аренды сервера любой конфигурации!
Гравитационный скачок что это
Гравитационный манёвр, она же гравитационная праща, так же реже пертурбационный манёвр.
У нас есть КА, небесное тело, а так же спутник небесного тела.
КА двигается со скоростью N относительно небесного тела. КА входит в гравитационный колодец спутника. КА летит прямо на спутник, но спутник уходит по орбите, и тем самым увеличивает скорость КА, и на выходе из колодца спутника КА будет иметь скорость относительно материнского тела N+V, т.е. большую. Верно и обратное, если пустить КА не позади движения спутника по орбите, а перед ходом движения, скорость напротив уменьшится.
На примере.
Берём КА на орбите планеты Кербин. Пускаем его на сближение с муной. Для взлёта с низкой орбиты до муны, где-то 700-900 дельты в зависимости от кривости низкой орбиты и кривости рук. Приближаем орбиту к поверхности муны как можно ближе. И улетаем в тартарары на орбиту сола, подняв орбиту лишь до муны.
Что это даёт.
При правильной реализации орбита будет значительно ближе к орбите планеты до которой планируется долететь.
Проблемы.
Вот мы проделали эту операцию, но видим, что наша солнечная орбита достаточно кривая и что с ней, что без неё мы затратим столько же топлива для межпланетных путешествий.
Как видно из анимации выше гравитационный манёвр неизбежно искривляет орбиту КА. А нам надо давить газ лишь в определённом направлении.
Как этого избежать.
Выходим на низкую орбиту. Ставьте маркер манёвра на орбите. Бегунками в нижней левой части экрана изменяем траекторию(6 кнопок векторов и 2 кнопки изменения точки манёвра), так что финальная орбита будет лететь строго по направлению движения орбиты Кербина, если мы летим к внешним планетам(Дюна, Дрес, Джул, Иилу) или же против навправления движения если мы летим к внутренним(Мохо, Ив) а так же Керболу(солу). В случае если нигде на орбите нету окон можно назначить маркер на последующие витки орбиты, нажимая + в области изменения маркера.
Так же, если траектория обрывается на выходе из гравитационного колодца, ставим ещё один маркер с нулевой дельтой. И тем самым продлеваем траекторию. Или же в настройках увеличить «Предел прогноза траек-рий».
Что бы избежать многолетних ожиданий на орбите пользуйтесь окнами запуска. Т.е. Летите к планете только в определённом положении, относительно Кербина.
Так же для достижения более далёких планет рекомендуется использовать манёвры связанные с планетами.
Вот примеры из реальной жизни.
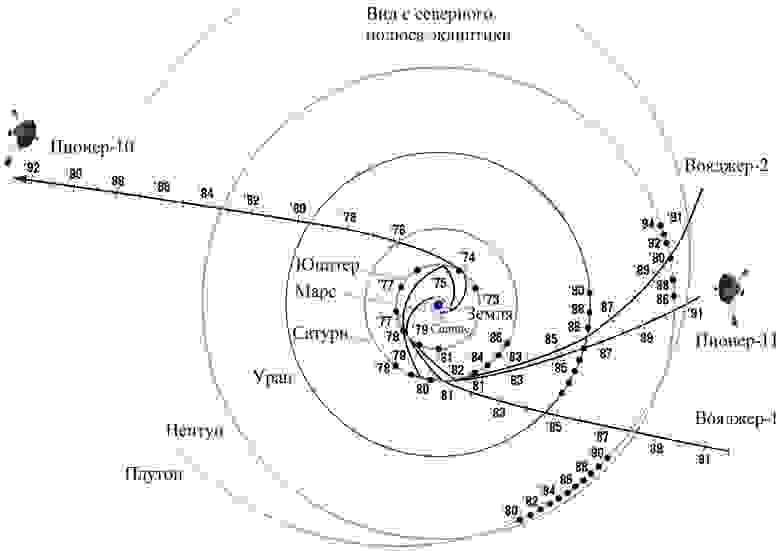
Вояджер 1 и 2.
Как видно из изображения используя гравитационный манёвр можно значительно увеличить скорость.
Юнона
Аппарат взлетел с Земли, произвёл гравитационный манёвр так же с Землёю.
Стоит понимать, что в отличие от реальности у КСП не бесконечный радиус притяжения, а ограничен конечной сферой. И не все конфигурации траектории могут быть реализованы в игре.
В игре же это выглядит примерно так
Осуществляются же множественные витки возможно лишь убив не один час в планировщике траекторий.
Гравитационный манёвр является наиболее экономичным способом межпланетных путешествий. Но придётся мириться с потерей времени ввиду того что не всегда имеется полётное окно позволяющее добраться до цели на том же витке. Но в теории можно добраться почти до каждого объекта почти не тратясь на горючее.
Формула света
Новая картина Мироздания
Гравитационный манёвр
Если ракета пролетит рядом с планетой, её скорость изменится. Либо уменьшится, либо возрастёт. Это зависит от того, с какой стороны от планеты она пролетит.
1. Гравитационные манёвры Вояджера
Когда американские космические аппараты «Вояджеры» совершали свой знаменитый Гранд тур по внешней Солнечной системе, они выполнили несколько так называемых гравитационных манёвров вблизи планет-гигантов.
Больше всего повезло «Вояджеру-2», который пролетел мимо всех четырёх больших планет. График его скорости см. на рисунке:
Из графика видно, что после каждого сближения с планетой (кроме Нептуна), скорость космического аппарата возрастала на несколько километров в секунду.
На первый взгляд это может показаться странным: объект влетает в гравитационное поле и ускоряется, затем вылетает из поля и тормозится. Скорость прилёта должна равняться скорости вылета. Откуда появляется дополнительная энергия?
Дополнительная энергия появляется потому, что есть третье тело – Солнце. При пролёте рядом с планетой космический аппарат обменивается с ней импульсом и энергией. Если при таком обмене гравитационная энергия планеты в поле Солнца уменьшается, то кинетическая энергия космического аппарата (КА) увеличивается, и наоборот.
Как должен пролететь мимо планеты КА, чтобы его скорость возросла? Ответить на этот вопрос нетрудно. Пусть КА пересечет орбиту планеты прямо перед ней. В этом случае, получив дополнительный импульс в направлении на планету, он передаст ей дополнительный импульс в противоположном направлении, то есть в направлении её движения. В результате планета перейдёт на чуть более высокую орбиту, и её энергия возрастёт. Энергия КА при этом, соответственно, уменьшится. Если же КА пересечёт орбиту позади планеты, то он, чуть-чуть притормозив её движение, переведёт планету на более низкую орбиту. Скорость КА при этом возрастёт.
Конечно, масса КА несоизмерима с массой планеты. Поэтому изменение орбитальных параметров планеты при гравитационном манёвре бесконечно малая величина, не поддающаяся измерению. Тем не менее, энергия планеты изменяется, и мы можем убедиться в этом, проведя гравитационный манёвр и увидев, что скорость КА изменяется. Вот, к примеру, как пролетел «Вояджер-2» вблизи Юпитера 9 июля 1979 года (см. рис.). При подлёте к Юпитеру скорость космического аппарата составляла 10 км/сек. В момент максимального сближения она увеличилась до 28 км/сек. А после того, как «Вояджер-2» вылетел из гравитационного поля газового гиганта, уменьшилась до 20 км/сек. Таким образом, в результате гравитационного манёвра скорость космического аппарата возросла в два раза и стал гиперболической. То есть превысила скорость, необходимую для вылета из Солнечной системы. На орбите Юпитера скорость вылета из Солнечной системы около 18 км/сек.
Из этого примера видно, что Юпитер (или другая планета) может разогнать какое-нибудь тело до гиперболической скорости. А значит, он может «выбросить» это тело из Солнечной системы. Может быть, современные космогонисты правы? Может быть, действительно планеты-гиганты выбросили ледяные глыбы на далёкие окраины Солнечной системы и, таким образом, сформировали кометное облако Оорта.
Прежде чем ответить на этот вопрос, посмотрим, на какие гравитационные манёвры способны планеты?
2. Принципы гравитационного манёвра
Впервые я познакомился с гравитационным манёвром в 9-м классе на краевой олимпиаде по физике. Задача была такая. С Земли стартует ракета со скоростью V (достаточна, чтобы вылететь из поля притяжения). У ракеты есть двигатель с тягой F, который может работать время t. В какой момент времени нужно включить двигатель, чтобы конечная скорость ракеты была максимальная? Сопротивлением воздуха пренебречь.
Сначала мне показалось, что не важно, когда включить двигатель. Ведь вследствие закона сохранения энергии, конечная скорость ракеты должна быть одинаковой в любом случае. Оставалось посчитать конечную скорость ракеты в двух случаях: 1. двигатель включаем в начале, 2. двигатель включаем после вылета из поля притяжения Земли. После чего сравнить результаты и убедиться, что конечная скорость ракеты в обоих случаях одинакова. Но потом я вспомнил, что мощность равна: сила тяги умножить на скорость. Поэтому мощность ракетного двигателя будет максимальна, если включить двигатель сразу на старте, когда скорость ракеты максимальна. Итак, правильный ответ: двигатель включаем сразу же, тогда конечная скорость ракеты будет максимальной.
И хотя я задачу решил правильно, но проблема осталась. Конечная скорость, а, значит, и энергия ракеты ЗАВИСИТ от того, в какой момент времени включить двигатель. Вроде бы явное нарушение закона сохранения энергии. Или нет? В чём тут дело? Энергия должна сохраняться! На все эти вопросы я пытался ответить уже после олимпиады.
Пусть у нас есть ракета массы М с двигателем, который создаёт тягу силой F. Поместим эту ракету в пустое пространство (вдали от звёзд и планет) и включим двигатель. С каким ускорением будет двигаться ракета? Ответ мы знаем из Второго закона Ньютона: ускорение a равно:
Теперь перейдём в другую инерциальную систему отсчёта, в которой ракета движется с большой скоростью, скажем, 100 км/сек. Чему равно ускорение ракеты в этой системе отсчёта?
Ускорение НЕ ЗАВИСИТ от выбора инерциальной системы отсчёта, поэтому оно будет ТЕМ ЖЕ САМЫМ:
Масса ракеты также не изменяется (100 км/сек это ещё не релятивистский случай), поэтому и сила тяги F будет ТОЙ ЖЕ САМОЙ. И, следовательно, мощность ракеты ЗАВИСИТ от её скорости. Ведь мощность равна силе, умноженной на скорость. Получается, что если ракета движется со скоростью 100 км/сек, то мощность её двигателя в 100 раз мощнее, чем ТОЧНО ТАКОГО ЖЕ двигателя, находящегося на ракете, движущейся со скоростью 1 км/сек.
На первый взгляд это может показаться странным и даже парадоксальным. Откуда берётся огромная дополнительная мощность? Энергия ведь должна сохраняться!
Давайте разберёмся в этом вопросе.

Ракета всегда движется на реактивной тяге: она выбрасывает в космос различные газы с высокой скоростью. Для определённости предположим, что скорость выброса газов 10 км/сек. Если ракета движется со скоростью 1 км/сек, то её двигатель разгоняет в основном не ракету, а ракетное топливо. Поэтому мощность двигателя по разгону ракеты не высока. А вот если ракета движется со скоростью 10 км/сек, то выброшенное топливо будет ПОКОИТЬСЯ относительно внешнего наблюдателя, то есть, вся мощность двигателя будет тратится на разгон ракеты. А если ракета движется со скоростью 100 км/сек? В этом случае выброшенное топливо будет двигаться со скоростью 90 км/сек. То есть, скорость топлива УМЕНЬШИТСЯ от 100 до 90 км/сек. И ВСЯ разность кинетической энергии топлива в силу закона сохранения энергии будет передана ракете. Поэтому мощность ракетного двигателя при таких скоростях значительно возрастёт.
Проще говоря, у быстро двигающейся ракеты её топливо обладает огромной кинетической энергией. И из этой энергии черпается дополнительная мощность для разгона ракеты. Теперь осталось сообразить, как это свойство ракеты можно использовать на практике.
3. Практическое применение
Предположим, в недалёком будущем вы собрались лететь на ракете в систему Сатурна на Титан:
чтобы исследовать анаэробные формы жизни.
Долетели до орбиты Юпитера и выяснилось, что скорость ракеты упала почти до нуля. Не рассчитали как следует траекторию полёта или топливо оказалось контрафактным. А может, метеорит попал в топливный отсек, и почти всё топливо было потеряно. Что делать?
У ракеты есть двигатель и остался небольшой запас горючего. Но максимум, на что способен двигатель – увеличить скорость ракеты на 1 км/сек. Этого явно недостаточно, чтобы долететь до Сатурна. И вот пилот предлагает такой вариант.
«Входим в поле притяжения Юпитера и падаем на него. В результате Юпитер разгоняет ракету до огромной скорости – примерно 60 км/сек. Когда ракета разгонится до этой скорости, включаем двигатель. Мощность двигателя при такой скорости возрастёт многократно. Затем вылетаем из поля притяжения Юпитера. В результате такого гравитационного манёвра скорость ракеты возрастает не на 1 км/сек, а значительно больше. И мы сможем долететь до Сатурна».
Но кто-то возражает.
«Да, мощность ракеты вблизи Юпитера возрастёт. Ракета получит дополнительную энергию. Но, вылетая из поля притяжения Юпитера, мы всю эту дополнительную энергию потеряем. Энергия должна остаться в потенциальной яме Юпитера, иначе будет что-то вроде вечного двигателя, а это невозможно. Поэтому пользы от гравитационного манёвра не будет. Только зря время потратим».
Что вы об этом думаете?
Итак, ракета находится недалеко от Юпитера и почти неподвижна относительно него. У ракеты есть двигатель с топливом, которого хватит, чтобы увеличить скорость ракеты только на 1 км/сек. Чтобы повысить КПД двигателя, предлагается совершить гравитационный манёвр: «уронить» ракету на Юпитер. Она будет двигаться в его поле притяжения по параболе (см. фото). И в самой низкой точке траектории (помечена красным крестиком на фото) включить двигатель. Скорость ракеты вблизи Юпитера составит 60 км/сек. После того, как двигатель её дополнительно разгонит, скорость ракеты возрастёт до 61 км/сек. Какая скорость будет у ракеты, когда она вылетит из поля притяжения Юпитера?
Эта задача по силам школьнику старших классов, если, конечно, он хорошо знает физику. Сначала нужно написать формулу для суммы потенциальной и кинетической энергий. Затем вспомнить формулу для потенциальной энергии в поле тяготения шара. Посмотреть в справочнике, чему равна гравитационная постоянная, а также масса Юпитера и его радиус. Используя закон сохранения энергии и произведя алгебраические преобразования, получить общую конечную формулу. И наконец, подставив в формулу все числа и проделав вычисления, получить ответ. Я понимаю, что никому (почти никому) не охота вникать в какие-то формулы, поэтому постараюсь, не напрягая вас никакими уравнениями, объяснить решение этой задачи «на пальцах». Надеюсь, получится!
Если ракета неподвижна, её кинетическая энергия равна нулю. А если ракета движется со скоростью 1 км/сек, то будем считать, что её энергия 1 единица. Соответственно, если ракета движется со скоростью 2 км/сек, то её энергия 4 единицы, если 10 км/сек, то 100 единиц и т.д. Это понятно. Половину задачи мы уже решили.
В точке, помеченной крестиком:
скорость ракеты 60 км/сек, а энергия 3600 единиц. 3600 единиц достаточно, чтобы вылететь из поля притяжения Юпитера. После разгона ракеты её скорость стала 61 км/сек, а энергия, соответственно, 61 в квадрате (берём калькулятор) 3721 единицы. Когда ракета вылетает из поля притяжения Юпитера, она тратит только 3600 единиц. Остаётся 121 единица. Это соответствует скорости (берём корень квадратный) 11 км/сек. Задача решена. Это не приближённый, а ТОЧНЫЙ ответ.
Мы видим, что гравитационный манёвр можно использовать для получения дополнительной энергии. Вместо того, чтобы разогнать ракету до 1 км/сек, её можно разогнать до 11 км/сек (энергия в 121 раз больше, КПД – 12 тысяч процентов!), если рядом будет какое-нибудь массивное тело вроде Юпитера.
За счёт чего мы получили ОГРОМНЫЙ энергетический выигрыш? За счёт того, что оставили израсходованное топливо не в пустом пространстве вблизи ракеты, а в глубокой потенциальной яме, созданной Юпитером. Израсходованное топливо получило большую потенциальную энергию со знаком МИНУС. Поэтому ракета получила большую кинетическую энергию со знаком ПЛЮС.
4. Поворот вектора скорости вблизи планеты
Предположим, мы пролетаем на ракете вблизи Юпитера и хотим увеличить её скорость. Но топлива у нас НЕТ. Скажем так, у нас есть немного топлива, чтобы подкорректировать свой курс. Но его явно недостаточно, чтобы заметно разогнать ракету. Можем ли мы заметно увеличить скорость ракеты, используя гравитационный манёвр?
В самом общем виде эта задача выглядит так. Мы влетаем в поле тяготения Юпитера с какой-то скоростью. Затем вылетаем из поля. Изменится ли наша скорость? И как сильно она может измениться? Давайте решим эту задачу.
С точки зрения наблюдателя, который находится на Юпитере (а точнее, неподвижен относительно его центра масс), наш манёвр выглядит так. Сначала ракета находится на большом расстоянии от Юпитера и движется к нему со скоростью V. Затем, приближаясь к Юпитеру, она разгоняется. Траектория ракеты при этом искривляется и, как известно, в самом общем виде представляет собой гиперболу. Максимальная скорость ракеты будет при минимальном сближении. Здесь главное – не врезаться в Юпитер, а пролететь рядом с ним. После минимального сближения ракета начнёт удаляться от Юпитера, а её скорость будет уменьшаться. Наконец, ракета вылетит из поля притяжения Юпитера. Какая у неё будет скорость? Точно такая же, как и была при влёте. Ракета влетела в гравитационное поле Юпитера со скоростью V и вылетела из него с точно такой же скоростью V. Ничего не изменилось? Нет изменилось. Изменилось НАПРАВЛЕНИЕ скорости. Это важно. Благодаря этому мы можем совершить гравитационный манёвр.
Действительно, для нас ведь важна не скорость ракеты относительно Юпитера, а её скорость относительно Солнца. Это так называемая гелиоцентрическая скорость. С такой скоростью ракета движется по Солнечной системе. Юпитер тоже движется по Солнечной системе. Вектор гелиоцентрической скорости ракеты можно разложить на сумму двух векторов: орбитальная скорость Юпитера (примерно 13 км/сек) и скорость ракеты ОТНОСИТЕЛЬНО Юпитера. Здесь нет ничего сложного! Это обычное правило треугольника для сложения векторов, которое изучают в 7-м классе. И этого правила ДОСТАТОЧНО, чтобы понять суть гравитационного манёвра.
У нас есть четыре скорости. V1 – это скорость нашей ракеты относительно Солнца ПЕРЕД гравитационным манёвром. U1 – это скорость ракеты относительно Юпитера ПЕРЕД гравитационным манёвром. U2 – это скорость ракеты относительно Юпитера ПОСЛЕ гравитационного манёвра. По величине U1 и U2 РАВНЫ, но по направлению они РАЗНЫЕ. V2 – это скорость ракеты относительно Солнца ПОСЛЕ гравитационного манёвра. Чтобы увидеть, как все эти четыре скорости связаны между собой, посмотрим на рисунок:
Зелёная стрелка АО – это скорость движения Юпитера по своей орбите. Красная стрелка АВ – это V1: скорость нашей ракеты относительно Солнца ПЕРЕД гравитационным манёвром. Жёлтая стрелка ОВ – это скорость нашей ракеты относительно Юпитера ПЕРЕД гравитационным манёвром. Жёлтая стрелка ОС – это скорость ракеты относительно Юпитера ПОСЛЕ гравитационного манёвра. Эта скорость ДОЛЖНА лежать где-то на жёлтой окружности радиуса ОВ. Потому что в своей системе координат Юпитер НЕ МОЖЕТ изменить величину скорости ракеты, а может только повернуть её на некоторый угол (альфа). И наконец, АС – это то, что нам нужно: скорость ракеты V2 ПОСЛЕ гравитационного манёвра.
Посмотрите, как всё просто. Скорость ракеты ПОСЛЕ гравитационного манёвра АС равна скорости ракеты ДО гравитационного манёвра АВ плюс вектор ВС. А вектор ВС это ИЗМЕНЕНИЕ скорости ракеты в системе отсчёта Юпитера. Потому что ОС – ОВ = ОС + ВО = ВО + ОС = ВС. Чем сильнее повернётся вектор скорости ракеты относительно Юпитера, тем эффективнее будет гравитационный манёвр.
Итак, ракета БЕЗ горючего влетает в поле притяжения Юпитера (или другой планеты). Величина её скорости ДО и ПОСЛЕ манёвра относительно Юпитера НЕ ИЗМЕНЯЕТСЯ. Но из-за поворота вектора скорости относительно Юпитера, скорость ракеты относительно Юпитера всё-таки изменяется. И вектор этого изменения просто прибавляется к вектору скорости ракеты ДО манёвра. Надеюсь, всё понятно объяснил.