Что такое показатель адиабаты

Показатели адиабаты: определение и процесс

При изучении поведения газов в физике много внимания уделяется изопроцессам, то есть таким переходам между состояниями системы, во время которых сохраняется один термодинамический параметр. Тем не менее, существует газовый переход между состояниями, который не является изопроцессом, но который играет важную роль в природе и технике. Речь идет об адиабатическом процессе. В данной статье рассмотрим его подробнее, акцентируя внимание на том, что такое показатель адиабаты газа.

Адиабатический процесс

Вам будет интересно: Задачи социологии: предметы, основные методы, цели и развитие

Согласно термодинамическому определению, под адиабатическим процессом понимают такой переход между начальным и конечным состояниями системы, в результате которого не существует обмена теплом между внешней средой и изучаемой системой. Такой процесс возможен при наличии следующих двух условий:

В технике адиабатный переход используют как для разогрева газа при его резком сжатии, так и для его охлаждения во время быстрого расширения. В природе рассматриваемый термодинамический переход проявляет себя, когда воздушная масса поднимается или опускается по склону холма. Такие подъемы и спуски приводят к изменению точки росы в воздухе и к возникновению осадков.

Уравнение Пуассона для адиабаты идеального газа

Вам будет интересно: Что такое плиз? Молодежный сленг

Идеальный газ представляет собой систему, в которой частицы движутся хаотично с большими скоростями, не взаимодействуют друг с другом и являются безразмерными. Такая модель является очень простой с точки зрения ее математического описания.

Согласно определению адиабатного процесса, можно записать следующее выражение в соответствии с первым законом термодинамики:

Иными словами, газ, расширяясь или сжимаясь, совершает работу P*dV за счет соответствующего изменения своей внутренней энергии dU.

В случае идеального газа, если воспользоваться уравнением его состояния (закон Клапейрона-Менделеева), то можно получить следующее выражение:

Это равенство называется уравнением Пуассона. Люди, которые знакомы с физикой газов, заметят, что если величина γ будет равна 1, то уравнение Пуассона перейдет в закон Бойля-Мариотта (изотермический процесс). Однако такое преобразование уравнений невозможно, поскольку γ для любого типа идеального газа больше единицы. Величина γ (гамма) называется показателем адиабаты идеального газа. Рассмотрим подробнее его физический смысл.

Что такое показатель адиабаты?

Поскольку γ всегда больше одного, то он показывает, во сколько раз изобарная теплоемкость изучаемой газовой системы превышает аналогичную изохорную характеристику.

Теплоемкости CP и CV

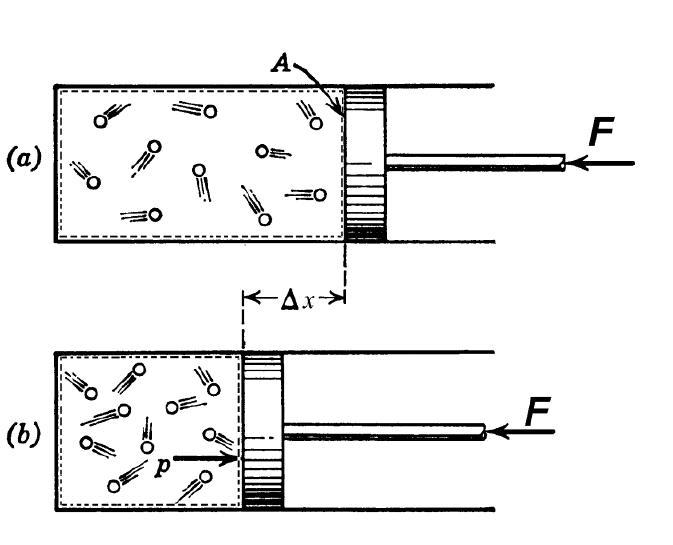
Чтобы определить показатель адиабаты, следует хорошо понимать смысл величин CP и CV. Для этого проведем следующий мысленный эксперимент: представим, что газ находится в закрытой системе в сосуде с твердыми стенками. Если нагревать сосуд, то все сообщенное тепло в идеальном случае перейдет во внутреннюю энергию газа. В такой ситуации будет справедливо равенство:

Величина CV определяет количество теплоты, которое следует передать системе, чтобы изохорно нагреть ее на 1 К.

Теперь предположим, что газ находится в сосуде с подвижным поршнем. В процессе нагрева такой системы поршень будет перемещаться, обеспечивая поддержание постоянного давления. Поскольку энтальпия системы в таком случае будет равна произведению изобарной теплоемкости на изменение температуры, то первый закон термодинамики примет вид:

Отсюда видно, что CP>CV, так как в случае изобарного изменения состояний необходимо расходовать тепло не только на повышение температуры системы, а значит, и ее внутренней энергии, но и на выполнение газом работы при его расширении.

Величина γ для газа идеального одноатомного

Самой простой газовой системой является одноатомный идеальный газ. Предположим, что мы имеет 1 моль такого газа. Напомним, что в процессе изобарного нагрева 1 моль газа всего на 1 Кельвин, он совершает работу, равную величине R. Этим символом принято обозначать универсальную газовую постоянную. Она равна 8,314 Дж/(моль*К). Применяя последнее выражение в предыдущем пункте для данного случая, получаем такое равенство:

Откуда можно определить значение изохорной теплоемкости CV:

Известно, что для одного моль одноатомного газа значение изохорной теплоемкости составляет:

Из последних двух равенств следует значение показателя адиабаты:

Отметим, что величина γ зависит исключительно от внутренних свойств самого газа (от многоатомности его молекул) и не зависит от количества вещества в системе.

Зависимость γ от числа степеней свободы

Выше было записано уравнение для изохорной теплоемкости одноатомного газа. Появившийся в нем коэффициент 3/2 связан с количеством степеней свободы у одного атома. У него существует возможность двигаться только в одном из трех направлений пространства, то есть существуют только поступательные степени свободы.

Если система образована двухатомными молекулами, то к трем поступательным добавляются еще две вращательные степени. Поэтому выражение для CV приобретает вид:

Тогда значение γ будет равно:

Отметим, что на самом деле существует у двухатомной молекулы еще одна колебательная степень свободы, но при температурах в несколько сотен Кельвин она не задействуется и не вносит вклад в теплоемкость.

Если молекулы газа состоят из более, чем двух атомов, тогда у них будет 6 степеней свободы. Показатель адиабаты при этом будет равен:

Таким образом, при увеличении числа атомов в молекуле газа величина γ уменьшается. Если построить график адиабаты в осях P-V, то можно заметить, что кривая для одноатомного газа будет вести себя более резко, чем для многоатомного.

Показатель адиабаты для смеси газов

Выше мы показали, что величина γ от химического состава газовой системы не зависит. Однако она зависит от количества атомов, которое составляет ее молекулы. Предположим, что система состоит из N компонент. Атомная доля компонента i в смеси равна ai. Тогда для определения показателя адиабаты смеси можно использовать следующее выражение:

Например, это выражение можно применить для определения γ воздуха. Поскольку он состоит на 99 % из двухатомных молекул кислорода и азота, то его показатель адиабаты должен быть очень близок к значению 1,4, что подтверждается при экспериментальном определении этой величины.

Источник

Показатели адиабаты: определение и процесс

При изучении поведения газов в физике много внимания уделяется изопроцессам, то есть таким переходам между состояниями системы, во время которых сохраняется один термодинамический параметр. Тем не менее, существует газовый переход между состояниями, который не является изопроцессом, но который играет важную роль в природе и технике. Речь идет об адиабатическом процессе. В данной статье рассмотрим его подробнее, акцентируя внимание на том, что такое показатель адиабаты газа.

Адиабатический процесс

Согласно термодинамическому определению, под адиабатическим процессом понимают такой переход между начальным и конечным состояниями системы, в результате которого не существует обмена теплом между внешней средой и изучаемой системой. Такой процесс возможен при наличии следующих двух условий:

В технике адиабатный переход используют как для разогрева газа при его резком сжатии, так и для его охлаждения во время быстрого расширения. В природе рассматриваемый термодинамический переход проявляет себя, когда воздушная масса поднимается или опускается по склону холма. Такие подъемы и спуски приводят к изменению точки росы в воздухе и к возникновению осадков.

Уравнение Пуассона для адиабаты идеального газа

Идеальный газ представляет собой систему, в которой частицы движутся хаотично с большими скоростями, не взаимодействуют друг с другом и являются безразмерными. Такая модель является очень простой с точки зрения ее математического описания.

Согласно определению адиабатного процесса, можно записать следующее выражение в соответствии с первым законом термодинамики:

Иными словами, газ, расширяясь или сжимаясь, совершает работу P*dV за счет соответствующего изменения своей внутренней энергии dU.

В случае идеального газа, если воспользоваться уравнением его состояния (закон Клапейрона-Менделеева), то можно получить следующее выражение:

Это равенство называется уравнением Пуассона. Люди, которые знакомы с физикой газов, заметят, что если величина γ будет равна 1, то уравнение Пуассона перейдет в закон Бойля-Мариотта (изотермический процесс). Однако такое преобразование уравнений невозможно, поскольку γ для любого типа идеального газа больше единицы. Величина γ (гамма) называется показателем адиабаты идеального газа. Рассмотрим подробнее его физический смысл.

Что такое показатель адиабаты?

Поскольку γ всегда больше одного, то он показывает, во сколько раз изобарная теплоемкость изучаемой газовой системы превышает аналогичную изохорную характеристику.

Теплоемкости CP и CV

Чтобы определить показатель адиабаты, следует хорошо понимать смысл величин C_P и C_V. Для этого проведем следующий мысленный эксперимент: представим, что газ находится в закрытой системе в сосуде с твердыми стенками. Если нагревать сосуд, то все сообщенное тепло в идеальном случае перейдет во внутреннюю энергию газа. В такой ситуации будет справедливо равенство:

Величина C_V определяет количество теплоты, которое следует передать системе, чтобы изохорно нагреть ее на 1 К.

Теперь предположим, что газ находится в сосуде с подвижным поршнем. В процессе нагрева такой системы поршень будет перемещаться, обеспечивая поддержание постоянного давления. Поскольку энтальпия системы в таком случае будет равна произведению изобарной теплоемкости на изменение температуры, то первый закон термодинамики примет вид:

Отсюда видно, что C_P>C_V, так как в случае изобарного изменения состояний необходимо расходовать тепло не только на повышение температуры системы, а значит, и ее внутренней энергии, но и на выполнение газом работы при его расширении.

Величина γ для газа идеального одноатомного

Самой простой газовой системой является одноатомный идеальный газ. Предположим, что мы имеет 1 моль такого газа. Напомним, что в процессе изобарного нагрева 1 моль газа всего на 1 Кельвин, он совершает работу, равную величине R. Этим символом принято обозначать универсальную газовую постоянную. Она равна 8,314 Дж/(моль*К). Применяя последнее выражение в предыдущем пункте для данного случая, получаем такое равенство:

Откуда можно определить значение изохорной теплоемкости C_V:

Известно, что для одного моль одноатомного газа значение изохорной теплоемкости составляет:

Из последних двух равенств следует значение показателя адиабаты:

Отметим, что величина γ зависит исключительно от внутренних свойств самого газа (от многоатомности его молекул) и не зависит от количества вещества в системе.

Зависимость γ от числа степеней свободы

Выше было записано уравнение для изохорной теплоемкости одноатомного газа. Появившийся в нем коэффициент 3/2 связан с количеством степеней свободы у одного атома. У него существует возможность двигаться только в одном из трех направлений пространства, то есть существуют только поступательные степени свободы.

Если система образована двухатомными молекулами, то к трем поступательным добавляются еще две вращательные степени. Поэтому выражение для C_V приобретает вид:

Тогда значение γ будет равно:

Отметим, что на самом деле существует у двухатомной молекулы еще одна колебательная степень свободы, но при температурах в несколько сотен Кельвин она не задействуется и не вносит вклад в теплоемкость.

Если молекулы газа состоят из более, чем двух атомов, тогда у них будет 6 степеней свободы. Показатель адиабаты при этом будет равен:

Таким образом, при увеличении числа атомов в молекуле газа величина γ уменьшается. Если построить график адиабаты в осях P-V, то можно заметить, что кривая для одноатомного газа будет вести себя более резко, чем для многоатомного.

Показатель адиабаты для смеси газов

Выше мы показали, что величина γ от химического состава газовой системы не зависит. Однако она зависит от количества атомов, которое составляет ее молекулы. Предположим, что система состоит из N компонент. Атомная доля компонента i в смеси равна a_i. Тогда для определения показателя адиабаты смеси можно использовать следующее выражение:

Например, это выражение можно применить для определения γ воздуха. Поскольку он состоит на 99 % из двухатомных молекул кислорода и азота, то его показатель адиабаты должен быть очень близок к значению 1,4, что подтверждается при экспериментальном определении этой величины.

Источник

Уравнение Пуассона для адиабатного процесса

Описание адиабатного процесса

Адиабатный или адиабатический процесс – это процесс, который протекает с небольшой скоростью при отсутствии теплового обмена с окружающей средой.

Адиабатный процесс является разновидностью термодинамического процесса. Важными условиями его возникновения являются теплоизолированная система и условия, при которых полностью исключается теплообмен с окружающей средой. При проведении практических исследований Q = 0. По первому закону термодинамики требуется полный расход выполненной работы для изменения внутренней энергии системы:

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

Такие результаты практически недостижимы при реальных условиях. Причина заключается в отсутствии идеальных теплоизоляционных материалов. Однако ученым удалось максимально приблизиться к созданию подходящих условий.

Например, благодаря применению оболочек, которые характеризуются низкими параметрами теплопроводности, создаются условия, как в термосе. Другим способом выступает достижение достаточно большой скорости протекания адиабатного процесса. В этом случае система обменивается теплом с окружающей средой в течение короткого промежутка времени, которым можно пренебречь при расчетах.

Уравнение Пуассона

При возникновении адиабатного процесса наблюдается одновременное изменение трех характеристик, которыми обладает газообразное вещество: V, p, Т. Величины зависят друг от друга, что выражается в уравнении Клапейрона-Менделеева. Корректно представить описание процесса можно, дополняя формулу уравнением Пуассона.

Формулировка отражает наличие зависимости между объемом и давлением газа. Исходя из первого принципа термодинамики, уравнение для адиабатного процесса в случае идеального газа будет выглядеть следующим образом:

Удаляя из уравнения выражение dT по уравнению Клапейрона-Менделеева, получается следующее равенство:

\(dT=\frac<1>\left(pdV+V dp \right)\)

В результате будет записана формула:

Исходя из уравнения Майера,

Необходимо подставить эту формулу, а также поделить числитель и знаменатель дроби перед скобками на \(CV\) и обозначить \(CP/CV\) – \(\gamma\)

Можно сделать следующий вывод:

В результате интеграции данного уравнения получается следующее соотношение:

\(\ln p+\gamma \ln V=\ln C\)

где С является постоянной величиной интегрирования.

Если пропотенциировать последнюю формулу, то в итоге получается уравнение Пуссона:

Коэффициент Пуассона

Показатель адиабаты равен отношению теплоемкости в условиях постоянного давления к теплоемкости в условиях постоянного объема.

Показатель адиабаты по-другому называют коэффициентом Пуассона или фактором изоэнтропийного расширения. Для обозначения этой величины используют греческую букву γ (гамма) или κ (каппа). Такие специальные символы применимы для решения задач химических инженерных дисциплин. Если решается задача по теплотехнике, целесообразно изображать коэффициент Пуассона в виде латинской буквы k.

Показатель адиабаты рассчитывают из отношения между изобарной теплоемкостью газообразного вещества и его изохорной теплоемкостью. Формула имеет следующий вид:

В разных газах показатель адиабаты будет неодинаковым. Для идеального газообразного вещества коэффициент Пуассона составляет 5/3, для двухатомного – 7/3, для трехатомного – 4/3.

Применение уравнения в расчетах ДВС и холодильных установок

В условиях реальных газов имеют значения силы, которые возникают при взаимодействии молекул друг с другом. Для расчета показателя адиабаты исследованных газообразных веществ требуется проводить эксперименты. В 1819 году учеными Клеманом и Дезормом были предложены методики определения коэффициента Пуассона. Описание эксперимента:

В этом случае показатель адиабаты будет иметь следующий вид:

После расчетов показатель адиабаты будет больше 1. Это объясняет постоянное возрастание температуры во время адиабатического сжатия идеального или реального газа. В случае расширения газообразного вещества, температурные показатели снижаются. Описанное явление носит название пневматического огнива. Это свойство адиабатического процесса применяют при конструировании двигателей, функционирующих на дизельном топливе. Горючая смесь в агрегате сжимается, находясь в специальном цилиндре, и воспламеняется под действием высокой температуры.

Уравнение Пуассона применимо не только для разработки двигателей внутреннего сгорания, но и активно применяется для осуществления расчетов в проектировании холодильного оборудования. Формула Пуассона позволяет с максимальной точностью описать равновесный адиабатный процесс, при условии которого состояния равновесия непрерывно сменяют друг друга. Если в реальных обстоятельствах открыть кран в баллоне, что приведет к адиабатному расширению газа, можно будет наблюдать нестационарный переходный процесс, сопровождающийся завихрениями газообразного вещества, которые со временем затухают по причине макроскопического трения.

Источник

Новое в блогах

Часть 3. Экспериментальная проверка

Ну, а теперь настало время перейти к самому интересному вопросу – к вопросу экспериментальной проверки моих теоретических выводов.

Самый простой, и, казалось бы, самый действенный способ проверки для обычного гражданина – заглянуть в справочники. Вот, например, что заявил мне гайд-паркер Юрий Евгеньевич Виноградов: «Открываю несколько справочников и вижу, что для одноатомных газов показатель адиабаты от 1,6 до 1,66». Моя теория предполагает величину показателя адиабаты, равной 1,33. Казалось бы, вопрос закрыт окончательно и бесповоротно?

В 1690 году профессор математики коллежа Мазарини Пьер Варинь о н написал в одной из свих книг : «Но вскоре мы понимаем, что вещи, которые представлялись нам очень простыми и очень легкими для понимания, когда мы смотрим на них в целом и поверхностно, представляются весьма трудными, весьма сложными, как только мы хотим более детально вникнуть в их суть . »

Так давайте, уважаемый читатель, попробуем вместе вникнуть в суть показателя адиабаты, также известной под именем «коэффициент Пуассона». Я потратил некоторое время на то, чтобы разобраться, какое отношение к адиабатным процессам в газах имеет Симеон Дени Пуассон. Насколько я помнил из вузовского курса сопротивления материалов, коэффициент Пуассона показывает, во сколько раз изменяется поперечное сечение деформируемых твердых тел при их растяжении или сжатии. И применение этого названия к показателю адиабаты газов, на мой взгляд, весьма спорно. Точнее сказать – абсолютно неправильно.

p V ^k =co nst

Другое написание этого уравнения уже приводилось во введении этой статьи:

p= const / V^ k =co nst V ^(- k )

Таким образом получается, что показатель адиабаты оказался волею судеб трижды освящен именем знаменитого французского физика и математика (адиабата Пуасоона, уравнение Пуассона и коэффициент Пуассона).

Впервые экспериментально определить показатель адиабаты попытался Гей-Люсcак совместно с Вальтером в 1807 году. К сожалению, я до сих пор не смог найти методику и результаты этого эксперимента (если кто знает, дайте ссылку, где можно это прочесть – желательно первоисточник).

Чуть позже, в 1819 году, свою методику определения показателя адиабаты разработали Клеман и Дезорм. Забавно, но эта методика, несмотря на полнейшую своё несоответствие методикам проведения опытов, приведшем к открытию классических газовых законов Бойля-Мариотта, Гей-Люссака и Шарля, сохранилась до сих пор и до сих пор используется в образовательном процессе. Дело в том, что опыты Бойля, Мариотта, Шарля и Гей-Люссака проводились при неизменном количестве газа, а Клеман и Дезорм это правило нарушили, что и привело в конечном итоге к одному из величайших заблуждений человечества.

В методичке, цитирую, «Кратко рассматриваются теория теплоемкостей газов и один из методов определения показателя адиабаты. Студентам предлагается экспериментально определить показатель адиабаты воздуха.»

Вот как описывают составители этой методички, О.О. Глазунов (кафедра общей и космической физики), Ю.П Царегородцев и рецензент, кандидат физико-математических наук, доцент Л.И. Дорохова, метод Клемана-Дезорма, цитирую:

«Процесс выполнения работы можно условно разбить на два этапа, каждый из которых включает в себя адиабатный и изохорный процесс.

1-ый этап: При закрытом кране накачиваем в баллон небольшое количество воздуха и зажимаем шланг зажимом. При этом давление и температура в баллоне повысятся. Это адиабатный процесс. »

Повторюсь (повторение – мать учения). Все три классических газовых закона и уравнение Менделеева-Клапейрона основываются на экспериментах, в ходе которых количество газа в емкости никогда не меняется. Поэтому, «накачивая в баллон небольшое количество воздуха», а затем, на втором этапе, выпуская его из баллона, Клеман и Дезорм выходят за рамки применения классических газовых законов и уравнения Менделеева-Клапейрона. Именно поэтому метод определения показателя адиабаты Клемана-Дезорма неверен. Несмотря на то, что, как написано в другой методичке другого образовательного учреждения, «одним из простых и надежных методов определения является метод Клемана и Дезорма».

Вот еще пара ссылок на методички для студентов по определению показателя адиабаты тем же самым методом:

То есть, как видно, метод Клемана-Дезорма, несмотря на свою явную ущербность, до сих пор считается основным способом определения величин показателей адиабаты.

Теперь давайте обратимся к «нашему святому» – к газовой промышленности. Там вопрос куда серьёзнее, чем научные споры между двумя гипотезами (теориями). Там – деньги. Причем не просто деньги, а гигаденьги, говоря языком физики.

Естественно, что там, где вращаются гигаденьги, все показатели должны быть полностью регламентированы. Именно поэтому были разработаны Всероссийским научно-исследовательским центром стандартизации, информации и сертификации сырья, материалов и веществ (ВНИЦ СМВ) Госстандарта России; фирмой «Газприборавтоматика» акционерного общества «Газавтоматика» РАО «Газпром» ныне используются при поставках газа следующие стандарты:

ГОСТ 30319.0-96 Газ природный. Методы расчета физических свойств. Общие положения

ГОСТ 30319.1-96 Газ природный. Методы расчета физических свойств. Определение физических свойств природного газа, его компонентов и продуктов его переработки.

ГОСТ 30319.2-96 Газ природный. Методы расчета физических свойств. Определение коэффициента сжимаемости

ГОСТ 30319.3-96 Газ природный. Методы расчета физических свойств. Определение физических свойств по уравнению состояния.

Пункт 4.5 ГОСТ 30319.1-96, устанавливает, что, цитирую:

«4.2 Показатель адиабаты зависит от параметров состояния газа (давления и температуры), а в случае смеси газов и от состава смеси.

4.3 Показатель адиабаты для чистых газов необходимо определять по ГСССД Р127 и другим материалам, рекомендуемым ГСССД.

4.5 Показатель адиабаты природного газа, метана и азота должен вычисляться по усовершенствованной формуле Кобза: »

Как видно, в этом явно эмпирическом уравнении, помимо давления p и температуры T используются еще и плотность газа ρ _c и некий довольно специфичный показатель x_a.

ГОСТ 30319.3-96 вообще предлагает использовать для расчета физических свойств природного газа, в том числе и показателя адиабаты разработанное ВНИЦ СМВ некое «уравнение состояния (УС)». При этом открыто заявляется, что расхождение величин показателя адиабаты, вычисленными по усовершенствованной формулой Кобза и при помощи уравнения стояния в диапазоне температур 240-360 К и давлении до 10 МПа при p/T

Интересно, а какой метод для фактического определения величин показателя адиабаты при различных условиях используют разработчики ГОСТов и составители ГСССД? Ведь все эти внушающие суеверный трепет и неосознанное уважение длиннющие эмпирические формулы с десятками непонятных коэффициентов основаны на каких-то опытных данных. Неужели используется всё тот же «простой и надежный метод определения» – метод Клемана и Дезорма? Если кто знает, расскажите.

Правда, кое-где начаты попытки изобрести новые методы определения показателя адиабаты. Например, с СПбГУ родился резонансный метод измерения показателя адиабаты воздуха http://physics.spbstu.ru/forstudents/labpractice/physics/Lab_1_08_Phys.pdf (© Кафедра экспериментальной физики СПбГПУ). При котором показатель адиабаты вычисляется неким собственным частотам колебаний поршня в трубке с адиабатически сжимаемым воздухом.

Лично мне до сих пор непонятно – а что именно мешает измерить показатель адиабаты действительно самым простым и самым понятным способом – простым измерением давления в цилиндре с поршнем?

Неужели до этого способа за 200 лет, прошедшие со времени опытов Клемана и Дезорма никто, ни в одной академии наук ни одной страны мира не смог додуматься?

Так как подбить кого-нибудь на проведение подобного опыта в нормально оснащенной лаборатории мне не удалось, то пришлось проводить такой опыт в «кухонных» условиях.

Для поршня было изготовлено специальное устройство, позволяющее закрепить его и создавать давление на шток посредством винта, имеющего шаг резьбы 1 мм – чтобы можно было легко определять степень сжатия газа внутри цилиндра. Степень сжатия газа n определяется как отношение текущего объёма в замкнутой полости цилиндра к начальному объёму.

Примечание – температура действительно минус 1°С – только что эта «экспериментальная установка» была вытащена из холодильника, где находилась несколько часов, несмотря на мягкое недовольство жены. На корпусе пневмоцилиндра видна изморозь.

Информацию о характеристиках преобразователя давления от фирмы «Орлэкс» информацию можно найти здесь:

Фото 2. Преобразователь давления Д2,5 фирмы «Орлэкс» и резиновая прокладка.

Фото 3 Манометр ДМ-15-100-1- G в деле.

Через некоторое время после начала экспериментов я решил, что было бы не лишне контролировать температуру газа внутри цилиндра. В общем-то я не строил никаких иллюзий по данному поводу. Ясно, что даже при выборе самого миниатюрного датчика температуры, его теплоёмкость сопоставима с теплоёмкостью исследуемого объема газа. Для определения температуры газа датчик должен нагреться до температуры газа. А в процессе теплообмена между газом и датчиком температура газа падает быстрее, чем повышается температура датчика.

Но для проверки закона Бойля-Мариотта контроль температуры просто необходим. Для контроля температуры я купил два платиновых датчика 700-102AAB-B00 производства фирмы Honeywell (см. фото 4), обладающие следующими характеристиками:

Время отклика вода/воздух, c 0,4/2,0

Размер, мм 2,1 x 2,3 x 0,9

Фото 4. Терморезистивный датчик 700-102AAB-B00

Показания с собственноручно изготовленного термодатчика и с преобразователя давления снимались измерительной станцией в составе (см. фото 5).

— платы АЦП PCI-9114A Rev.A2 HG (High Gain) от фирмы AdLink, http://www.adlinktech.com/PD/web/PD_detail.php?pid=31 и

— клавиатура, мышь, монитор и блок питания, 5В от которого использовались и для питания преобразователя давления и мостового датчика температуры (через резистор 8,2 кОм)

Изначально я планировал проверить достоверность уравнения Пуассона по отношению к реальным адиабатам, а заодно проверить, насколько достоверно можно произвести изотермический процесс. Дело в том, что реально изотермический процесс произвести невозможно – ведь если мы будем бесконечно долго перемещать поршень в цилиндре на бесконечно малые величины, чтобы обеспечить постоянную температуру, то на это уйдёт бесконечное количество лет. А жизнь коротка… Так или иначе, любой реальный изотермический процесс может состоять из большого числа других процессов, например, маленьких адиабатных и маленьких изохорных – т.е. чуть-чуть сжали и ждём, пока вследствие теплообмена температура газа понизиться до исходной.

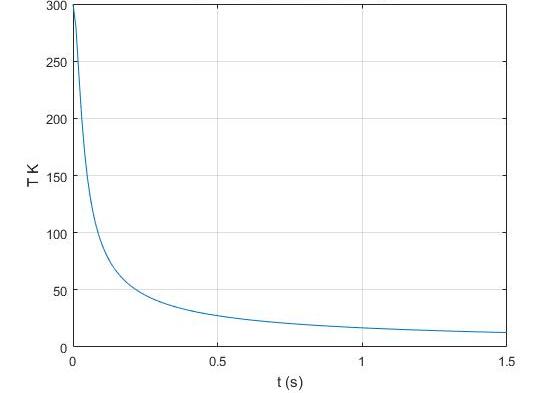
До начала «кухонных» экспериментов мне казалось, что воспроизвести адиабатный процесс будет значительно проще, чем изотермический. Я полагал, что процесс теплообмена между газом внутри поршня и поршнем будет происходить в течение десятков минут. Ан нет. Оказалось, что после очередного цикла сжатия газа при перемещении поршня на 1 мм, температура газа опускается до начальной в течение нескольких секунд. Из-за такой скорости теплообмена мой первоначальный план по исследованию адиабатных процессов был нарушен.

Итак. Перед началом экспериментов я рассуждал так: если быстро (допустим, в течение 10 секунд) завинчивать винт, газ внутри цилиндра при сжатии не будет успевать обмениваться теплотой с цилиндром. Если к тому же вращать винт с равномерной скоростью, АЦП снимет с преобразователя давления показатели, которые сами выстроятся в кривую, близкую к теоретической адиабате. Если же я буду завинчивать винт долго – с перерывами минуты, возможно, в десятки минут, то получу некое подобие изотермы.

Но, как я уже сказал, первые же результаты опровергли мои предположения и я решил сначала закончить серию экспериментов с проверкой закона Бойля-Мариотта. Однако, у меня этот закон не желал сходиться! Что за чертовщина. И я даже залез на какой-то из форумов (вроде это был dxdy) с наглым заявлением, что закон Бойля-Мариотта – чушь. Помимо других, этим заинтересовались и некоторые толковые преподаватели, один из которых порекомендовал мне не кипятиться раньше времени и поискать систематическую ошибку.

Однако – вопреки предположениям многочисленных теоретиков, которые сами ни разу не провели ни одного опыта, манометр был исправен, датчик давления – тоже, газ из цилиндра НЕ ТРАВИЛО, так как давление в 7-9 атм. не падали в течение недели, мыльная пена, которой я обмазывал для проверки стыки для проверки (способ старых газопроводчиков) нигде не пузырилась, а из полностью погруженного в воду устройства пузыри тоже нигде не вылезали. Надо сказать, что лента ФУМ оказалась отвратительным уплотнителем для газа, особенно когда я наполнял цилиндр гелием из воздушных шариков. Показания АЦП снимал исправно, и однажды я проверил это прибором Fluke-189.

Так как найти такое АЦП, стоимостью около 15000 руб и преобразователь давления не каждому под силу, проверить мой эксперимент можно и простым дешёвым манометром. В таблице 1, в графе «Абсолютное давление газа (по манометру)» приведены результаты, которые я снимал визуально с манометра, выжидая после каждого витка по 20-30 секунд. Высчитанное значение const = pV при этом, как видно из соответствующей графы, лежит в пределах ±4%, что вполне приемлемо для «кухонного» эксперимента.

После этого я перешёл к исследованию адиабатных процессов.

Конечно, величину перемещения поршня в цилиндре (для определения степени сжатия газа, относительную величину занимаемого им объема) было бы весьма предпочтительнее посредством прецизионного датчика линейных перемещений, выпускаемых той же самой фирмой Honeywell (12 000 – 18 000 руб), но в настоящий исторический момент такие траты из семейного бюджета я не могу себе позволить.

Поэтому я поступил проще – резко нажимал на поршень с разной силой, используя свой вес, фиксируя при этом максимальную величину перемещения поршня и максимальную величину давления газа. Процесс длился десятую доли секунды, поэтому говорить о том, что результаты не соответствуют общепринятым, определенным по методу Клемана-Дезорма якобы из-за скорого теплообмена между газом и цилиндром – глупо.

Полученные мной результаты говорят сами за себя. При исследовании адиабатного сжатия воздуха, находящегося в начале сжатия при атмосферном давлении и температурк от 0 до 25 градусов Цельсия, показатель адиабаты, полученный путем аппроксимирования результатов, равнялся не общепринятой величине в 1,4, а всего лишь 1,29.

Для гелия при тех же условиях показатель адиабаты у меня получился равным 1,32, что теоретически обосновано в первой части статьи. Надо сказать, что у меня есть определенные сомнения в чистоте проведения данного эксперимента. Скорее всего, в поршне у меня была гелиево-воздушная смесь. Кроме того, после долгих экспериментов с повышением и понижением температуры, цилиндр потихоньку начал приходить в негодность.

Тем не менее, я считаю, что провел эксперимент на достаточно высоком для кухонных условий уровне и, самое главное – обозначил проблему.

Теперь же дело – за Российской академией наук, Министерством образования и науки, высшими учебными заведениями и специализированными лабораториями.

Источник