Что таоке вертикальные углы
Что такое угол? Виды углов
Определение угла
Угол — это простая геометрическая фигура. Определение угла напрямую связано с понятием луча.
Луч — прямая линия, у которой есть начало, но нет конца, и продолжается она только в одну сторону.
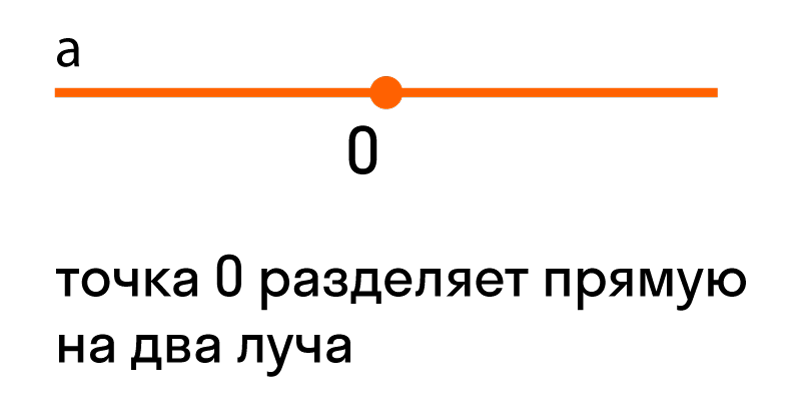
Если нам дана прямая a на плоскости, и на ней есть некоторая точка O — выходит, что прямая разделена точкой на две части, каждая из которых является лучом с началом в точке O.
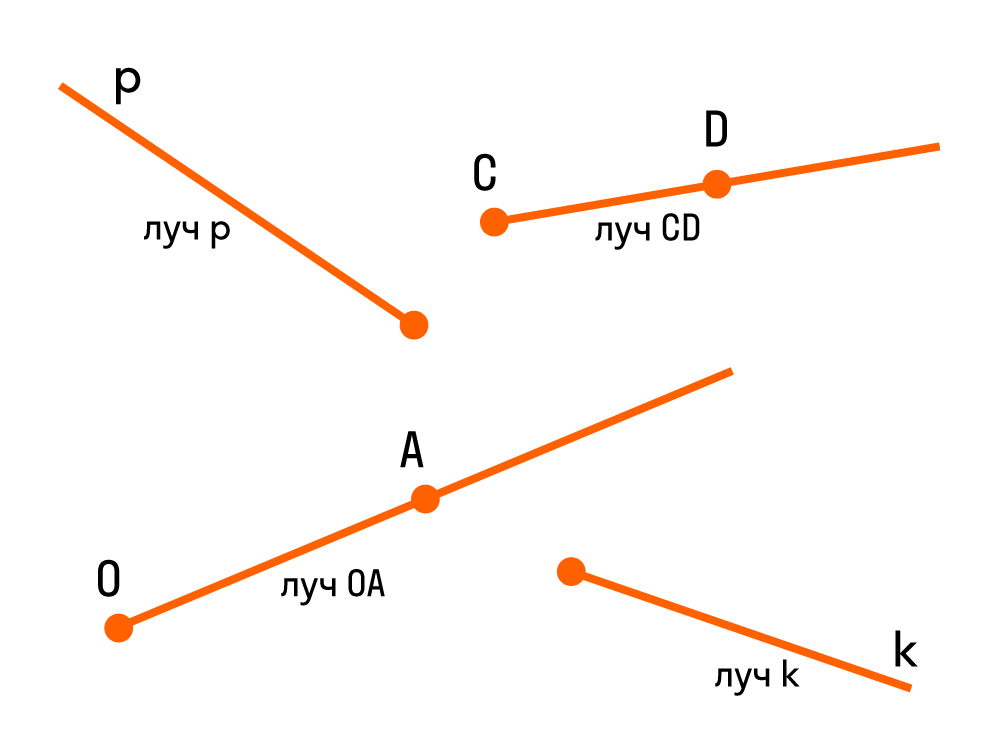
Луч можно обозначить одной строчной буквой латинского алфавита или двумя прописными. Например, вот так:
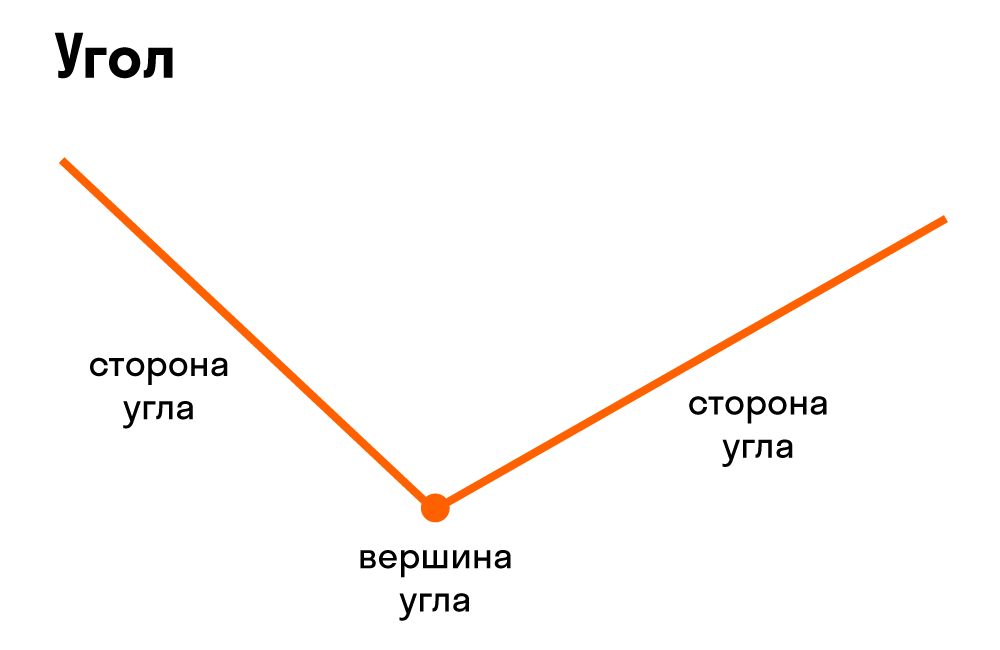
Угол — часть плоскости между двумя линиями, исходящими из одной точки. Каждая сторона угла является лучом, а вершина — общим началом сторон.
Что такое вершина и стороны угла
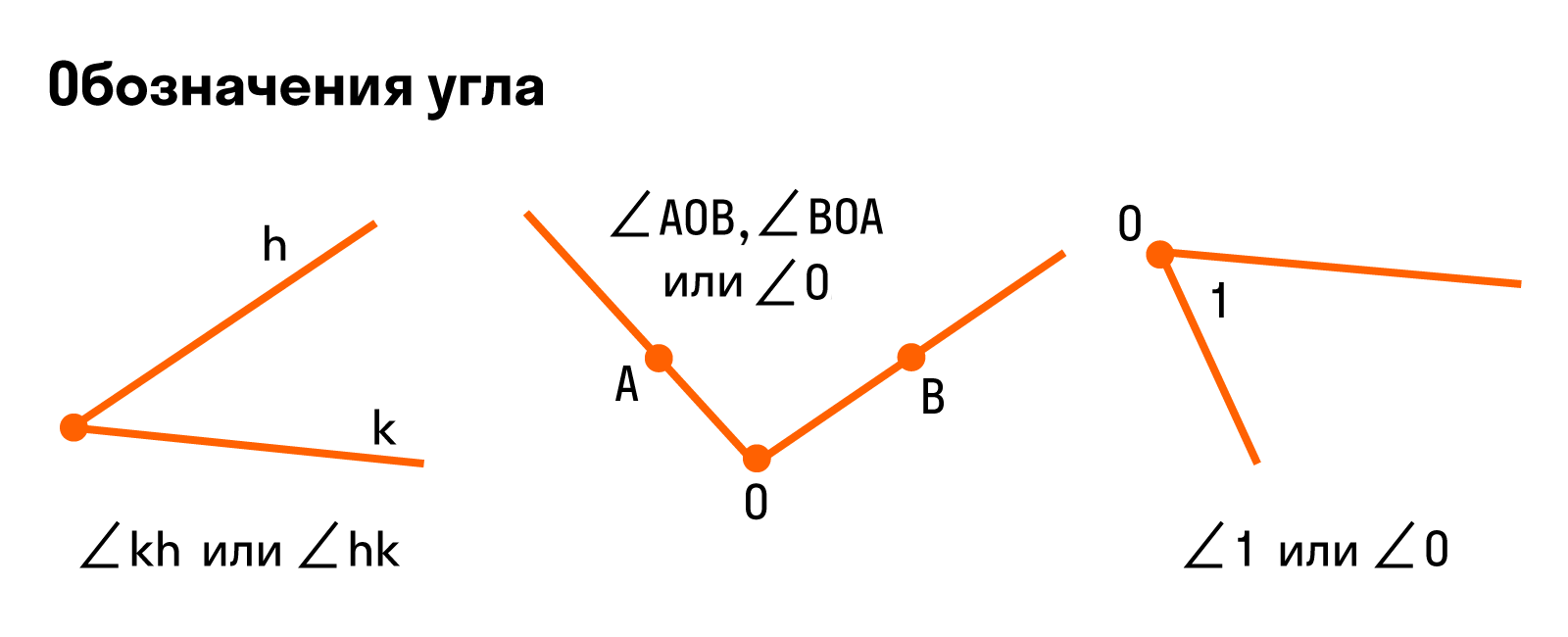
В математике существует специальный символ для обозначения угла, вот он: ∠.
Если стороны угла названы малыми латинскими буквами, то их записывают после символа. Например, так: ∠ab или ∠ba.
Если стороны угла названы большими буквами, то обозначение угла будет состоять из символа и трех букв, при этом вершина всегда записывается в центре. При сторонах угла OA и OB название угла запишем так: ∠AOB и ∠BOA. Также можно назвать угол одной большой буквой, которая указывает на его вершину, например: ∠O.
Иногда встречается обозначение в виде цифр — так тоже можно.
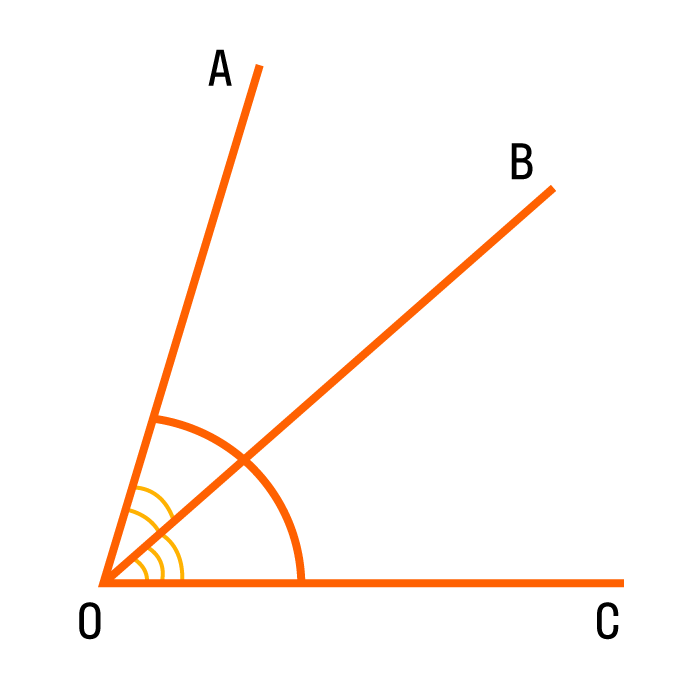
Для наглядности — все способы обозначения углов:
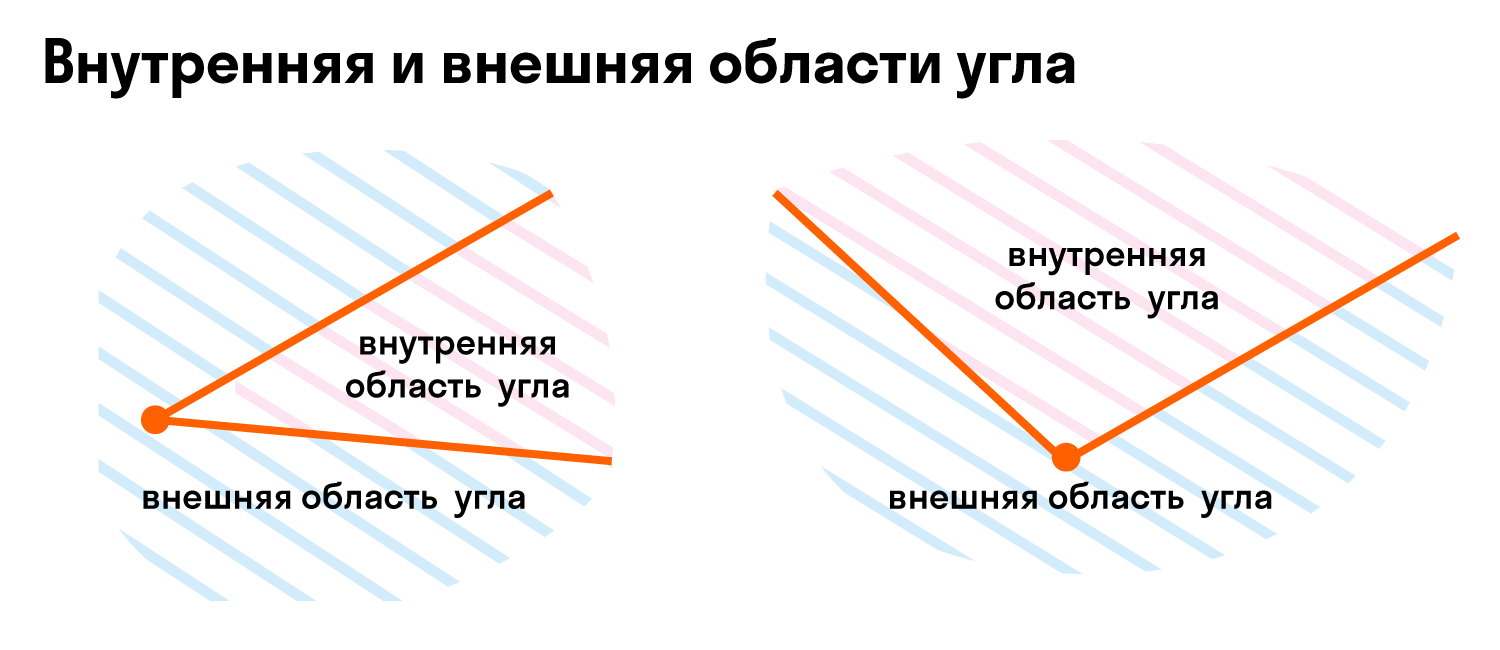
Так как угол делит плоскость на две части, одна будет внутренней областью угла, а другая — внешней областью угла. Вот так:
Единица измерения углов — градусы. Символ для обозначения градуса угла: °.
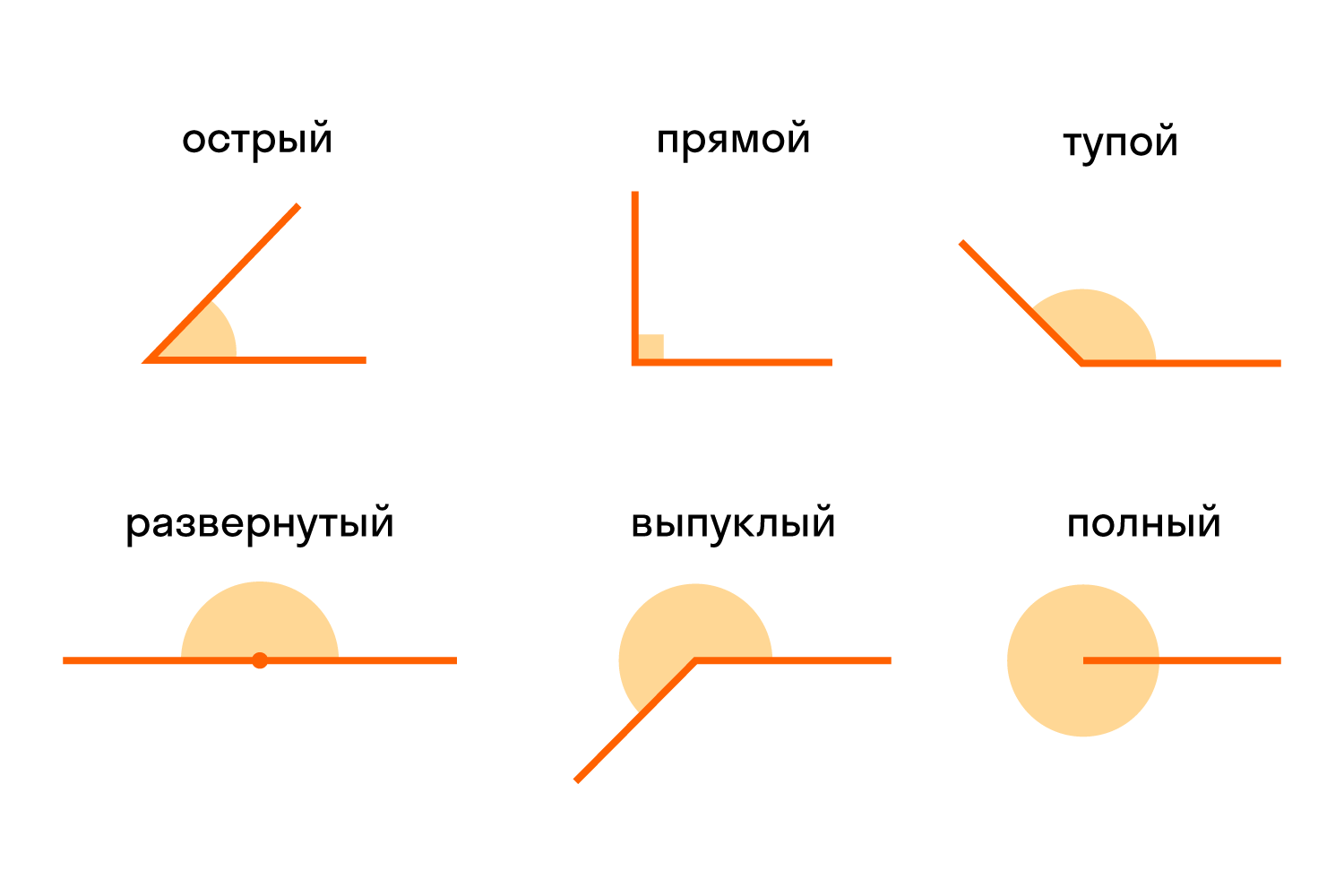
Виды углов
Есть разные типы углов и у каждого своё название:
Различать виды углов в геометрии важно. Определять можно на глаз или с помощью линейки.
Прямой угол — это угол, стороны которого перпендикулярны друг другу. Прямой угол всегда равен 90°.
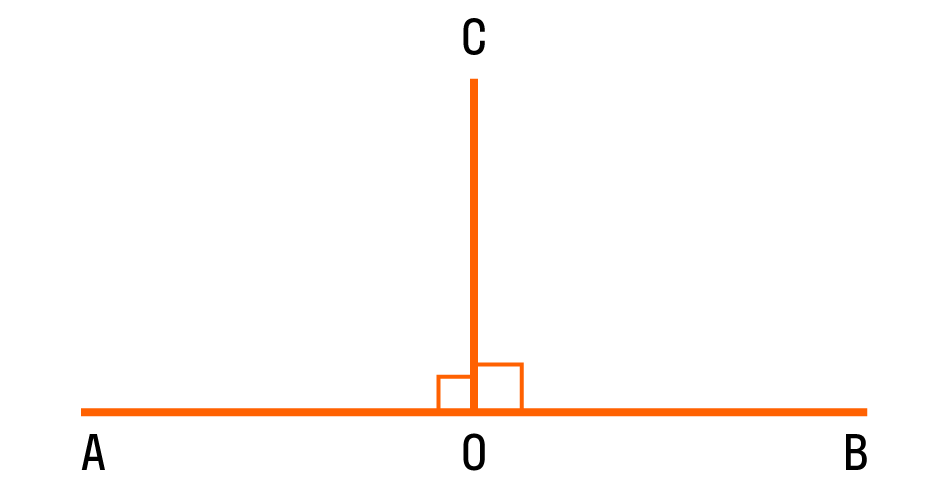
Если два смежных угла равны между собой, то каждый из них является прямым. Для удобства прямой угол обозначается уголком. Вот так:
На картинке изображены два прямых угла ∠AOC и ∠COB. Общая сторона OC перпендикулярна прямой AB, а точка O — основание перпендикуляра.
Острый угол — это угол, который меньше прямого угла, то есть
Сравнение углов
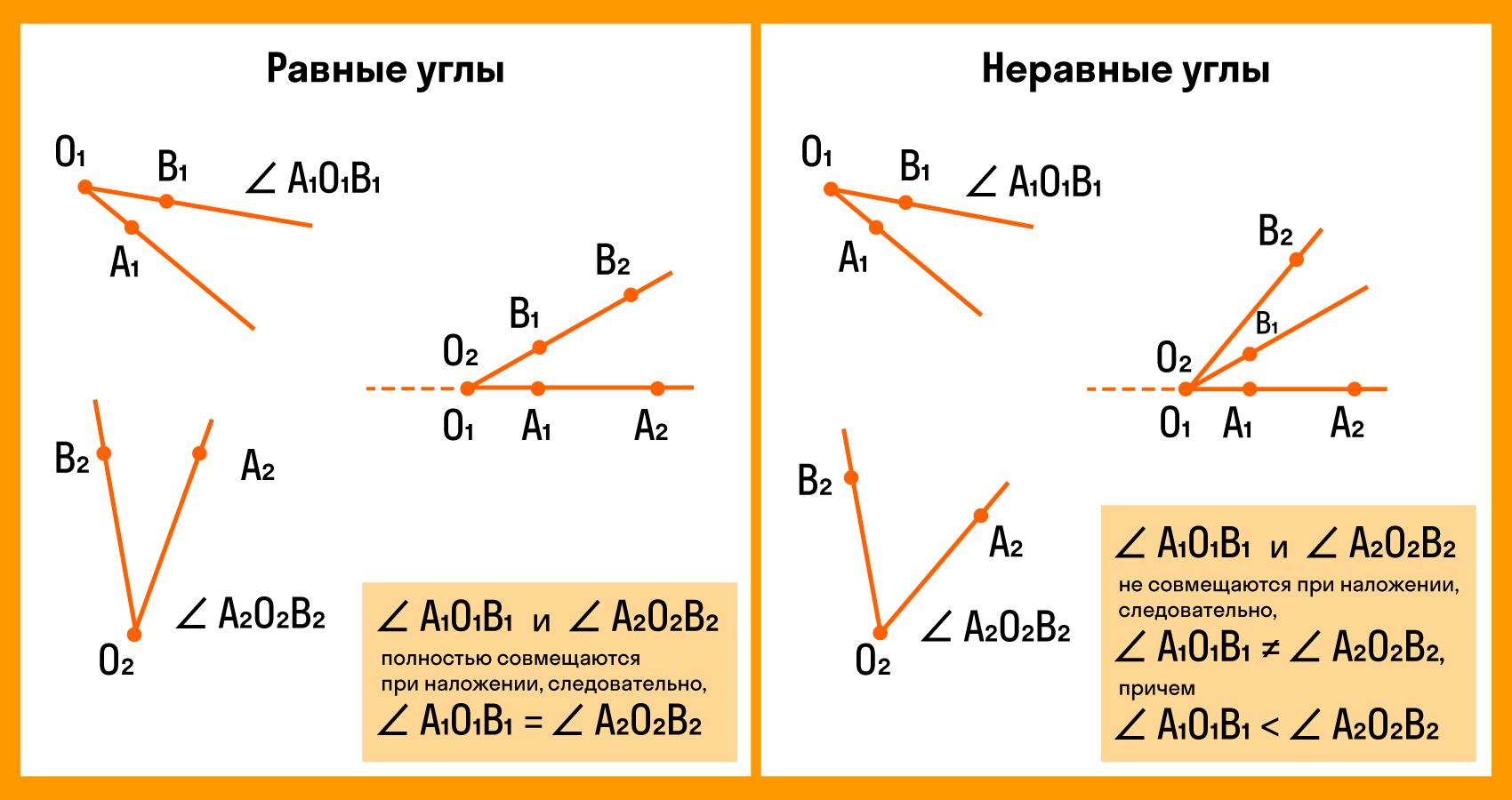
Для сравнения углов можно использовать самый простой способ из программы 4 класса — метод наложения. Для этого нужно совместить две вершины и сторону одного угла со стороной другого. Если стороны заданных углов совпадут, значит углы равные. Если нет, то угол, который лежит внутри другого, будет меньшим. Здесь два наглядных примера с равными и неравными углами:
При этом развернутые углы всегда являются равными.
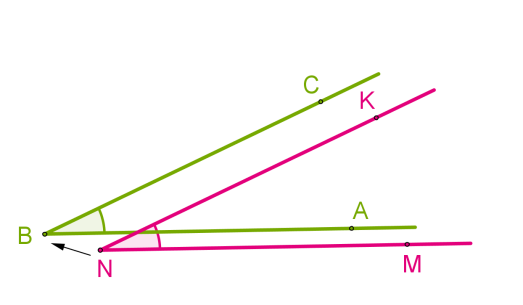
Совмещение углов ∠𝐴𝐵𝐶 и ∠𝑀𝑁𝐾 происходит следующим образом:
Если совпадут и другие стороны, то углы равны: ∠𝐴𝐵𝐶 = ∠𝑀𝑁𝐾.
Если нет, то один угол — меньше другого: ∠𝐴𝐵𝐶
Как правильно измерять углы
Измерение углов похоже на измерение отрезков: нужно сравнить их с углом, принятым за единицу измерения. В геометрии обычно за единицу измерения принимают градус — угол, равный 1/180 части развернутого угла. Он обозначается так: °.
Градусная мера угла — положительное число, которое показывает, сколько раз градус и его части укладываются в данном углу.
Есть еще две возможные меры угла: минуты и секунды. Они позволяют выполнять более точные расчеты, особенно, когда величина не является целым обозначением градуса.
Минута — 1/60 часть градуса. Обозначается ´.
Секунда — 1/60 часть минуты. Обозначается ´´.
Градус состоит из 3600 секунд, то есть: 1° = 60´ = 3600´´.
Как происходит измерение угла: сначала измеряют стороны угла, а после — его внутреннюю область. Всегда нужно считать количество уложенных углов, так как они предопределяют меру измеряемого угла.
Когда луч делит угол на два или более углов, градусная мера всего угла равна сумме градусных мер этих углов.
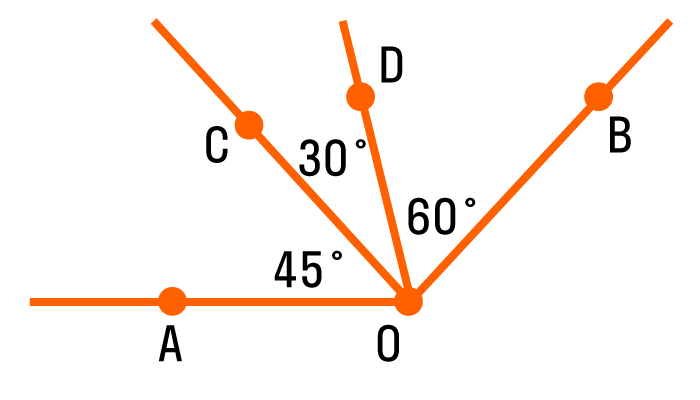
На рисунке изображен угол АОВ, он состоит из углов АОС, СОD и DОВ. Можно записать так: ∠AOB = ∠AOC + ∠COD + ∠DOB = 45° + 30° + 60° = 135 °.
Равные углы имеют равную градусную меру.
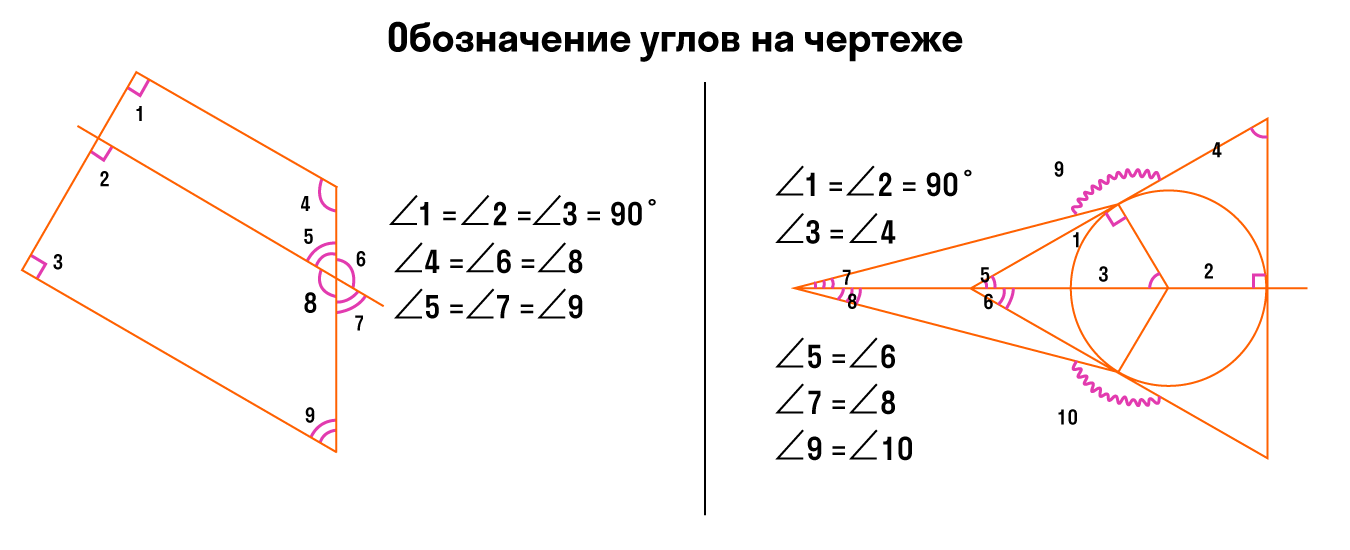
Обозначение углов на чертеже
Чертеж помогает решать задачки по геометрии в разы быстрее. Чтобы наглядно изображать углы и прочие фигуры, придумали даже отдельное направление — геометрический чертеж.
Задачи с углами могут быть разными, и не всегда есть возможность правильно изобразить и отметить угол. Вот что важно запомнить при обозначении лучей и углов:
На чертеже отмечены три неравных угла:
Для обозначения на чертеже более трех углов используем разные виды дуг: волнистые, зубчатые.
Обозначать углы можно разными цветами. Главное, чтобы было просто и броско. При этом не обязательно отмечать все-все углы — достаточно только тех, которые нам нужны для решения задачки.
Вертикальные углы
Какие углы вертикальные? Каким свойством обладают вертикальные углы?
Рассмотрим определение вертикальных углов и их свойство, а также применим свойство вертикальных углов для решения задач.
Определение.
Вертикальные углы — это пары углов с общей вершиной, которые образованы при пересечении двух прямых так, что стороны одного угла являются продолжением сторон другого.
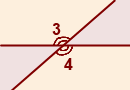
При пересечении двух прямых образуется две пары вертикальных углов:
∠1 и ∠2 — вертикальные углы
∠3 и ∠4 — вертикальные углы
Свойство вертикальных углов.
Вертикальные углы равны.
Таким образом, при пересечении двух прямых образуется две пары равных межу собой углов.
1) Сумма вертикальных углов равна 140º. Найти эти углы.
Так как вертикальные углы равны, а в условии сказано, что их сумма равна 140º, то каждый из них равен по 140:2=70º.
2) Сумма двух углов, образованных при пересечении двух прямых, равна 100º. Найти эти углы.
При пересечении двух прямых образуются углы двух видов — вертикальные и смежные.
Так как сумма смежных углов равна 180º, а по условию, сумма углов равна 100º, то эти углы — вертикальные.
А так как вертикальные углы равны, то каждый из них равен по 100:2=50º.
Вертикальные углы во многих задачах — важный элемент при доказательстве равенства треугольников и подобия треугольников.
Вертикальные углы и их свойства
Вертикальные углы и их свойства.
Вертикальные углы – это два угла с общей вершиной, которые образованы при пересечении двух прямых так, что стороны одного угла являются продолжением сторон другого
Вертикальные углы (понятие и определение):
Вертикальные углы – это два угла с общей вершиной, которые образованы при пересечении двух прямых так, что стороны одного угла являются продолжением сторон другого.
Две пары вертикальных углов образуют полный угол, т.е. угол, градусная мера которого равна 360°.
Рис. 1. Вертикальные углы
Вертикальные углы равны друг другу.
Свойства вертикальных углов:
1. При пересечении двух прямых образуются две пары вертикальных углов.
Рис. 2. Вертикальные углы
2. Синусы, косинусы и тангенсы вертикальных углов равны.
tg α = tg γ, tg β = tg δ
Примечание: © Фото https://www.pexels.com, https://pixabay.com
Мировая экономика
Справочники
Востребованные технологии
Поиск технологий
О чём данный сайт?
Настоящий сайт посвящен авторским научным разработкам в области экономики и научной идее осуществления Второй индустриализации России.
Он включает в себя:
– экономику Второй индустриализации России,
– теорию, методологию и инструментарий инновационного развития – осуществления Второй индустриализации России,
– организационный механизм осуществления Второй индустриализации России,
– справочник прорывных технологий.
Мы не продаем товары, технологии и пр. производителей и изобретателей! Необходимо обращаться к ним напрямую!
Мы проводим переговоры с производителями и изобретателями отечественных прорывных технологий и даем рекомендации по их использованию.
О Второй индустриализации
Осуществление Второй индустриализации России базируется на качественно новой научной основе (теории, методологии и инструментарии), разработанной авторами сайта.
Конечным результатом Второй индустриализации России является повышение благосостояния каждого члена общества: рядового человека, предприятия и государства.
Вторая индустриализация России есть совокупность научно-технических и иных инновационных идей, проектов и разработок, имеющих возможность быть широко реализованными в практике хозяйственной деятельности в короткие сроки (3-5 лет), которые обеспечат качественно новое прогрессивное развитие общества в предстоящие 50-75 лет.
Та из стран, которая первой осуществит этот комплексный прорыв – Россия, станет лидером в мировом сообществе и останется недосягаемой для других стран на века.
Вертикальные углы
В геометрии, два угла называются вертикальными, если они созданы пересечением двух прямых и не являются прилегающими. Такие углы имеют общую вершину. Они имеют одинаковую градусную меру и могут рассматриваться как равные.
Содержание
Теорема о вертикальных углах
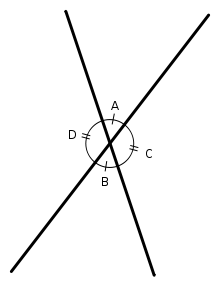
Алгебраическое решение вертикальных углов
Например, угол A на рисунке — неизвестен. Обозначим A = x. Если два прилегающих угла образуют прямую, то они — смежные. Тогда, градусная мера C = 180 − x. Аналогично, градусная мера D = 180 − x. Углы C и D имеют одинаковую меру, которая равна 180 — x и являются вертикальными. Поскольку, угол B является смежным для обоих углов C и D, для того, чтобы вычислить размер B можно использовать градусную меру любого из них. Используя меру угла C или угла D, найдём градусную меру угла B = 180 — (180 — x) = 180—180 + x = x. Отсюда, оба угла A и B имеют г
См. также
Литература
Ссылки
Полезное
Смотреть что такое «Вертикальные углы» в других словарях:
ВЕРТИКАЛЬНЫЕ УГЛЫ — см. Угол … Большой Энциклопедический словарь
Вертикальные углы — пары углов с общей вершиной, образуемые при пересечении двух прямых так, что стороны одного угла являются продолжением сторон другого. На рис. две пары В. у. Рис. к ст. Вертикальные углы … Большая советская энциклопедия
вертикальные углы — см. Угол. * * * ВЕРТИКАЛЬНЫЕ УГЛЫ ВЕРТИКАЛЬНЫЕ УГЛЫ, см. Угол (см. УГОЛ) … Энциклопедический словарь
ВЕРТИКАЛЬНЫЕ УГЛЫ — см. Угол … Естествознание. Энциклопедический словарь
углы геометрической видимости — Углы, определяющие зону минимального телесного угла, в которой должна быть видна видимая поверхность огня. Эта зона определяется сегментами сферы, центр которой совпадает с исходным центром огня, а экватор параллелен грунту. Эти сегменты… … Справочник технического переводчика
углы геометрической видимости — 2.12 углы геометрической видимости: Углы, определяющие зону минимального телесного угла, в которой должна быть видна видимая поверхность огня. Эта зона определяется сегментами сферы, центр которой совпадает с исходным центром огня, а экватор… … Словарь-справочник терминов нормативно-технической документации
Инсоляционные углы светопроема — горизонтальные и вертикальные углы, в пределах которых на плоскости светопроема возможно поступление прямых солнечных лучей. При расчете инсоляционных углов глубина световых проемов принимается равной расстоянию от наружной плоскости стены до… … Официальная терминология
ГЕОМЕТРИЯ — раздел математики, занимающийся изучением свойств различных фигур (точек, линий, углов, двумерных и трехмерных объектов), их размеров и взаимного расположения. Для удобства преподавания геометрию подразделяют на планиметрию и стереометрию. В… … Энциклопедия Кольера
Угол — У этого термина существуют и другие значения, см. Угол (значения). Угол ∠ Размерность ° Единицы измерения СИ Радиан … Википедия
ГОСТ Р ИСО 12509-2010: Машины землеройные. Осветительные, сигнальные и габаритные огни и светоотражатели — Терминология ГОСТ Р ИСО 12509 2010: Машины землеройные. Осветительные, сигнальные и габаритные огни и светоотражатели оригинал документа: 3.1.5 габаритная ширина (overall width): Расстояние между двумя вертикальными плоскостями объемного… … Словарь-справочник терминов нормативно-технической документации
Вертикальные углы. Свойства вертикальных углов
Определение 1. Вертикальными углами называются два угла, у которых стороны одного угла являются продолжениями сторон другого угла.
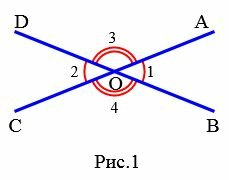 |
На Рис.1 углы AOB и COD вертикальные. Вертикальные также углы AOD и BOC.
Свойства вертикальных углов
1. Вертикальные углы равны.
2. Две пересекающие прямые образуют две пары вертикальных углов.
Доказательство пункта 1. Поскольку 1, 3 и 2, 3 смежные углы, то имеем
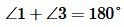 , , 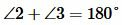 |
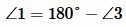 , , 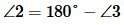 |
Следовательно 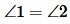
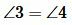
Задачи и решения
Задание 1. Угол 1 равен 32°. Найти углы 2, 3, 4 (Рис.2).
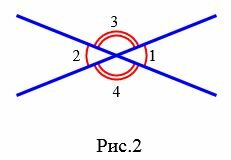 |
Решение. Так как углы 1 и 2 вертикальны, то 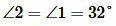
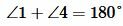
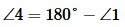 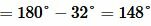 . . |
Углы 3 и 4 вертикальные. Тогда
Ответ. 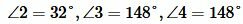
Задание 2. При пересечении двух прямых образовались четыре угла. Сумма двух углов равна 220°. Найти все углы.
Ответ.