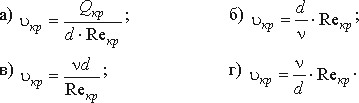Что является источником потерь энергии движущейся жидкости
Что является источником потерь энергии движущейся жидкости
4.1. Гидравлическое сопротивление это
а) сопротивление жидкости к изменению формы своего русла;
б) сопротивление, препятствующее свободному проходу жидкости;
в) сопротивление трубопровода, которое сопровождается потерями энергии жидкости;
г) сопротивление, при котором падает скорость движения жидкости по трубопроводу.
4.2. Что является источником потерь энергии движущейся жидкости?
а) плотность;
б) вязкость;
в) расход жидкости;
г) изменение направления движения.
4.3. На какие виды делятся гидравлические сопротивления?
а) линейные и квадратичные;
б) местные и нелинейные;
в) нелинейные и линейные;
г) местные и линейные.
4.4. Влияет ли режим движения жидкости на гидравлическое сопротивление
а) влияет;
б) не влияет;
в) влияет только при определенных условиях;
г) при наличии местных гидравлических сопротивлений.
4.5. Ламинарный режим движения жидкости это
а) режим, при котором частицы жидкости перемещаются бессистемно только у стенок трубопровода;
б) режим, при котором частицы жидкости в трубопроводе перемещаются бессистемно;
в) режим, при котором жидкость сохраняет определенный строй своих частиц;
г) режим, при котором частицы жидкости двигаются послойно только у стенок трубопровода.
4.6. Турбулентный режим движения жидкости это
а) режим, при котором частицы жидкости сохраняют определенный строй (движутся послойно);
б) режим, при котором частицы жидкости перемещаются в трубопроводе бессистемно;
в) режим, при котором частицы жидкости двигаются как послойно так и бессистемно;
г) режим, при котором частицы жидкости двигаются послойно только в центре трубопровода.
4.7. При каком режиме движения жидкости в трубопроводе пульсация скоростей и давлений не происходит?
а) при отсутствии движения жидкости;
б) при спокойном;
в) при турбулентном;
г) при ламинарном.
4.8. При каком режиме движения жидкости в трубопроводе наблюдается пульсация скоростей и давлений в трубопроводе?
а) при ламинарном;
б) при скоростном;
в) при турбулентном;
г) при отсутствии движения жидкости.
4.9. При ламинарном движении жидкости в трубопроводе наблюдаются следующие явления
а) пульсация скоростей и давлений;
б) отсутствие пульсации скоростей и давлений;
в) пульсация скоростей и отсутствие пульсации давлений;
г) пульсация давлений и отсутствие пульсации скоростей.
4.10. При турбулентном движении жидкости в трубопроводе наблюдаются следующие явления
а) пульсация скоростей и давлений;
б) отсутствие пульсации скоростей и давлений;
в) пульсация скоростей и отсутствие пульсации давлений;
г) пульсация давлений и отсутствие пульсации скоростей.
4.11. Где скорость движения жидкости максимальна при турбулентном режиме?
а) у стенок трубопровода;
б) в центре трубопровода;
в) может быть максимальна в любом месте;
г) все частицы движутся с одинаковой скоростью.
4.12. Где скорость движения жидкости максимальна при ламинарном режиме?
а) у стенок трубопровода;
б) в центре трубопровода;
в) может быть максимальна в любом месте;
г) в начале трубопровода.
4.13. Режим движения жидкости в трубопроводе это процесс
а) обратимый;
б) необратимый;
в) обратим при постоянном давлении;
г) необратим при изменяющейся скорости.
4.14. Критическая скорость, при которой наблюдается переход от ламинарного режима к турбулентному определяется по формуле
4.15. Число Рейнольдса определяется по формуле
4.16. От каких параметров зависит значение числа Рейнольдса?
а) от диаметра трубопровода, кинематической вязкости жидкости и скорости движения жидкости;
б) от расхода жидкости, от температуры жидкости, от длины трубопровода;
в) от динамической вязкости, от плотности и от скорости движения жидкости;
г) от скорости движения жидкости, от шероховатости стенок трубопровода, от вязкости жидкости.
4.17. Критическое значение числа Рейнольдса равно
4.18. При Re > 4000 режим движения жидкости
а) ламинарный;
б) переходный;
в) турбулентный;
г) кавитационный.
Ответы к тесту: Скорость движения жидкости параметры
⚑ Закажите написание студенческой работы!
Если возникли сложности с подготовкой студенческой работы, то можно доверить её выполнение специалистами нашей компании. Мы гарантируем исполнить заказ во время и без ошибок!
Тестовый вопрос: По мере движения жидкости от одного сечения к другому потерянный напор
Выберите правильный ответ:
[ верно ] увеличивается;
[неверно] остается постоянным;
[неверно] увеличивается при наличии местных сопротивлений.
Тестовый вопрос: Уровень жидкости в трубке Пито поднялся на высоту H = 15 см. Чему равна скорость жидкости в трубопроводе
Выберите правильный ответ:
[ верно ] 1,72 м/с;
Тестовый вопрос: Гидравлическое сопротивление это
Выберите правильный ответ:
[неверно] сопротивление жидкости к изменению формы своего русла;
[неверно] сопротивление, препятствующее свободному проходу жидкости;
[ верно ] сопротивление трубопровода, которое сопровождается потерями энергии жидкости;
[неверно] сопротивление, при котором падает скорость движения жидкости по трубопроводу.
Тестовый вопрос: Что является источником потерь энергии движущейся жидкости?
Выберите правильный ответ:
[ верно ] вязкость;
[неверно] расход жидкости;
[неверно] изменение направления движения.
Тестовый вопрос: На какие виды делятся гидравлические сопротивления?
Выберите правильный ответ:
[неверно] линейные и квадратичные;
[неверно] местные и нелинейные;
[неверно] нелинейные и линейные;
[ верно ] местные и линейные.
Тестовый вопрос: Влияет ли режим движения жидкости на гидравлическое сопротивление
Выберите правильный ответ:
[ верно ] влияет;
[неверно] влияет только при определенных условиях;
[неверно] при наличии местных гидравлических сопротивлений.
Тестовый вопрос: Ламинарный режим движения жидкости это
Выберите правильный ответ:
[неверно] режим, при котором частицы жидкости перемещаются бессистемно только у стенок трубопровода;
[неверно] режим, при котором частицы жидкости в трубопроводе перемещаются бессистемно;
[ верно ] режим, при котором жидкость сохраняет определенный строй своих частиц;
[неверно] режим, при котором частицы жидкости двигаются послойно только у стенок трубопровода.
Тестовый вопрос: Турбулентный режим движения жидкости это
Выберите правильный ответ:
[неверно] режим, при котором частицы жидкости сохраняют определенный строй (движутся послойно);
[ верно ] режим, при котором частицы жидкости перемещаются в трубопроводе бессистемно;
[неверно] режим, при котором частицы жидкости двигаются как послойно так и бессистемно;
[неверно] режим, при котором частицы жидкости двигаются послойно только в центре трубопровода.
Тестовый вопрос: При каком режиме движения жидкости в трубопроводе пульсация скоростей и давлений не происходит?
Выберите правильный ответ:
[неверно] при отсутствии движения жидкости;
[неверно] при спокойном;
[неверно] при турбулентном;
[ верно ] при ламинарном.
Тестовый вопрос: При каком режиме движения жидкости в трубопроводе наблюдается пульсация скоростей и давлений в трубопроводе?
Выберите правильный ответ:
[неверно] при ламинарном;
[неверно] при скоростном;
[ верно ] при турбулентном;
[неверно] при отсутствии движения жидкости.
Тестовый вопрос: При ламинарном движении жидкости в трубопроводе наблюдаются следующие явления
Выберите правильный ответ:
[неверно] пульсация скоростей и давлений;
[ верно ] отсутствие пульсации скоростей и давлений;
[неверно] пульсация скоростей и отсутствие пульсации давлений;
[неверно] пульсация давлений и отсутствие пульсации скоростей.
Тестовый вопрос: При турбулентном движении жидкости в трубопроводе наблюдаются следующие явления
Выберите правильный ответ:
[ верно ] пульсация скоростей и давлений;
[неверно] отсутствие пульсации скоростей и давлений;
[неверно] пульсация скоростей и отсутствие пульсации давлений;
[неверно] пульсация давлений и отсутствие пульсации скоростей.
Тестовый вопрос: Где скорость движения жидкости максимальна при турбулентном режиме?
Выберите правильный ответ:
[неверно] у стенок трубопровода;
[неверно] в центре трубопровода;
[ верно ] может быть максимальна в любом месте;
[неверно] все частицы движутся с одинаковой скоростью.
Тестовый вопрос: Где скорость движения жидкости максимальна при ламинарном режиме?
Выберите правильный ответ:
[неверно] у стенок трубопровода;
[ верно ] в центре трубопровода;
[неверно] может быть максимальна в любом месте;
[неверно] в начале трубопровода.
Тестовый вопрос: Режим движения жидкости в трубопроводе это процесс
Выберите правильный ответ:
[ верно ] обратимый;
[неверно] обратим при постоянном давлении;
[неверно] необратим при изменяющейся скорости.
Тестовый вопрос: От каких параметров зависит значение числа Рейнольдса?
Выберите правильный ответ:
[ верно ] от диаметра трубопровода, кинематической вязкости жидкости и скорости движения жидкости;
[неверно] от расхода жидкости, от температуры жидкости, от длины трубопровода;
[неверно] от динамической вязкости, от плотности и от скорости движения жидкости;
[неверно] от скорости движения жидкости, от шероховатости стенок трубопровода, от вязкости жидкости.
Что является источником потерь энергии движущейся жидкости
Следует заметить, что потери напора и по длине и в местных гидравлических сопротивлениях существенным образом зависят от так называемого режима движения жидкости.
Установка состоит из резервуара А с водой, от которого отходит стеклянная труба В с краном С на конце, и сосуда D с водным раствором краски, которая может по трубке вводиться тонкой струйкой внутрь стеклянной трубы В.
Первый случай движения жидкости. Если немного приоткрыть кран С и дать возможность воде протекать в трубе с небольшой скоростью, а затем с помощью крана Е впустить краску в поток воды, то увидим, что введенная в трубу краска не будет перемешиваться с потоком воды. Струйка краски будет отчетливо видимой вдоль всей стеклянной трубы, что указывает на слоистый характер течения жидкости и на отсутствие перемешивания. Если при этом, если к трубе подсоединить пьезометр или трубку Пито, то они покажут неизменность давления и скорости по времени. Такой режим движения называется ламинарный.
Второй случай движения жидкости. При постепенном увеличении скорости течения воды в трубе путем открытия крана С картина течения вначале не меняется, но затем при определенной скорости течения наступает быстрое ее изменение. Струйка краски по выходе из трубки начинает колебаться, затем размывается и перемешивается с потоком воды, причем становятся заметными вихреобразования и вращательное движение жидкости. Пьезометр и трубка Пито при этом покажут непрерывные пульсации давления и скорости в потоке воды. Такое течение называется турбулентным (рис.4.1, вверху).
Если уменьшить скорость потока, то восстановится ламинарное течение.
Итак, ламинарным называется слоистое течение без перемешивания частиц жидкости и без пульсации скорости и давления. При ламинарном течении жидкости в прямой трубе постоянного сечения все линии тока направлены параллельно оси трубы, при этом отсутствуют поперечные перемещения частиц жидкости.
Турбулентным называется течение, сопровождающееся интенсивным перемешиванием жидкости с пульсациями скоростей и давлений. Наряду с основным продольным перемещением жидкости наблюдаются поперечные перемещения и вращательные движения отдельных объемов жидкости. Переход от ламинарного режима к турбулентному наблюдается при определенной скорости движения жидкости. Эта скорость называется критической υ кр.
Значение этой скорости прямо пропорционально кинематической вязкости жидкости и обратно пропорционально диаметру трубы.
Входящий в эту формулу безразмерный коэффициент k, одинаков для всех жидкостей и газов, а также для любых диаметров труб. Этот коэффициент называется критическим числом Рейнольдса Reкр и определяется следующим образом:
Как показывает опыт, для труб круглого сечения Reкр примерно равно 2300.
Таким образом, критерий подобия Рейнольдса позволяет судить о режиме течения жидкости в трубе. При Re Reкр течение является турбулентным. Точнее говоря, вполне развитое турбулентное течение в трубах устанавливается лишь при Re примерно равно 4000, а при Re = 2300…4000 имеет место переходная, критическая область.
Режим движения жидкости напрямую влияет на степень гидравлического сопротивления трубопроводов.
В некоторых случаях при движении жидкости в закрытых руслах происходит явление, связанное с изменением агрегатного состояния жидкости, т.е. превращение ее в пар с выделением из жидкости растворенных в ней газов.
Наглядно это явление можно продемонстрировать на простом устройстве, состоящим из трубы, на отдельном участке которой установлена прозрачная трубка Вентури (рис.4.2). Вода под давлением движется от сечения 1-1 через сечение 2-2 к сечению 3-3. Как видно из рисунка, сечение 2-2 имеет меньший диаметр. Скорость течения жидкости в трубе можно изменять, например, установленным после сечения 3-3 краном.
При небольшой скорости никаких видимых изменений в движении жидкости не происходит. При увеличении скорости движения жидкости в узком сечении трубки Вентури 2-2 появляется отчетливая зона с образованием пузырьков газа. Образуется область местного кипения, т.е. образование пара с выделением растворенного в воде газа. Далее при подходе жидкости к сечению 3-3 это явление исчезает.
Это явление обусловлено следующим. Известно, что при движении жидкой или газообразной среды, давление в ней падает. Причем, чем выше скорость движения среды, тем давление в ней ниже. Поэтому, при течении жидкости через местное сужение 2-2, согласно уравнению неразрывности течений, увеличивается скорость с одновременным падением давления в этом месте. Если абсолютное давление при этом достигает значения равного давлению насыщенных паров жидкости при данной температуре или значения равного давлению, при котором начинается выделение из нее растворимых газов, то в данном месте потока наблюдается интенсивное парообразование (кипение) и выделение газов. Такое явление называется кавитацией.
При дальнейшем движении жидкости к сечению 3-3, пузырьки исчезают, т.е. происходит резкое уменьшение их размеров. В то время, когда пузырек исчезает (схлопывается), в точке его схлопывания происходит резкое увеличение давления, которое передается на соседние объемы жидкости и через них на стенки трубопровода. Таким образом, от таких многочисленных местных повышений давлений (гидроударов), возникает вибрация.
Кавитация в обычных случаях является нежелательным явлением, и ее не следует допускать в трубопроводах и других элементах гидросистем. Кавитация возникает в кранах, вентилях, задвижках, жиклерах и т.д.
Кавитация может иметь место в гидромашинах (насосах и гидротурбинах), снижая при этом их коэффициент полезного действия, а при длительном воздействии кавитации происходит разрушение деталей, подверженных вибрации. Кроме этого разрушаются стенки трубопроводов, уменьшается их пропускная способность вследствие уменьшения живого сечения трубы.
Уравнение, связывающее переменные υ и r, имеет следующий вид:
Теперь определим расход жидкости при ламинарном течении в круглой трубе. Так как эпюра распределения скоростей в круглой трубе имеет вид параболоида вращения с максимальным значением скорости в центре трубы, то расход жидкости численно равен объему этого параболоида. Определим этот объем.
Максимальная скорость дает высоту параболоида
Как известно из геометрии, объем параболоида высотой h и площадью ρR 2 равен
Если вместо R подставить диаметр трубы d, то формула (4.4) приобретет вид
Расход в трубе можно выразить через среднюю скорость:
Для определения потерь напора при ламинарном течении жидкости в круглой трубе рассмотрим участок трубы длиной l, по которому поток течет в условиях ламинарного режима (рис.4.3).
Потеря давления в трубопроводе будет равна
Если в формуле динамический коэффициент вязкости μ заменить через кинематический коэффициент вязкости υ и плотность ρ ( μ = υ ρ ) и разделить обе части равенства на объемный вес жидкости γ = ρ g, то получим:
Так как левая часть полученного равенства равна потерям напора hпот в трубе постоянного диаметра, то окончательно это равенство примет вид:
Уравнение может быть преобразовано в универсальную формулу Вейсбаха-Дарси, которая окончательно записывается так:
Однако при ламинарном режиме для определения коэффициента гидравлического трения λ Т.М. Башта рекомендует при Re
Как было указано в п.4.1, для турбулентного течения характерно перемешивание жидкости, пульсации скоростей и давлений. Если с помощью особо чувствительного прибора-самописца измерять пульсации, например, скорости по времени в фиксированной точке потока, то получим картину, подобную показанной на рис.4.4. Скорость беспорядочно колеблется около некоторого осредненного по времени значения υ оср, которое данном случае остается постоянным.
Характер линий тока в трубе в данный момент времени отличается большим разнообразием (рис.4.5).
Рис. 4.4. Пульсация скорости в турбулентном потоке. Рис. 4.5. Характер линий тока в турбулентном потоке
При турбулентном режиме движения жидкости в трубах эпюра распределения скоростей имеет вид, показанный на рис. 4.6. В тонком пристенном слое толщиной δ жидкость течет в ламинарном режиме, а остальные слои текут в турбулентном режиме, и называются турбулентным ядром. Таким образом, строго говоря, турбулентного движения в чистом виде не существует. Оно сопровождается ламинарным движением у стенок, хотя слой δ с ламинарным режимом весьма мал по сравнению с турбулентным ядром.
Основной расчетной формулой для потерь напора при турбулентном течении жидкости в круглых трубах является уже приводившаяся выше эмпирическая формула, называемая формулой Вейсбаха-Дарси и имеющая следующий вид:
Впервые наиболее исчерпывающей работы по определению были даны И.И. Никурадзе, который на основе опытных данных построил график зависимости lg(1000λ) от lg Re для ряда значений Δ/r 0. Опыты Никурадзе были проведены на трубах с искусственно заданной шероховатостью, полученной путем приклейки песчинок определенного размера на внутренние стенки трубопровода. Результаты этих исследований представлены на рис. 4.7, где построены кривые зависимости lg (1000λ) от lg Re для ряда значений Δ/r0.
Прямая I соответствует ламинарному режиму движения жидкости.
Далее на графике можно рассматривать три области.
Характерные значения Δэ (в мм) для труб из различных материалов приведены ниже:
| Стекло | 0 |
| Трубы, тянутые из латуни, свинца, меди | 0…0,002 |
| Высококачественные бесшовные стальные трубы | 0,06…0,2 |
| Стальные трубы | 0,1…0,5 |
| Чугунные асфальтированные трубы | 0,1…0,2 |
| Чугунные трубы | 0,2…1,0 |
Определение λ для этой области производят по упрощенной формуле Альтшуля:
Итак, потери напора, определяемые по формуле Вейсбаха-Дарси, можно определить, зная коэффициент гидравлического сопротивления, который определяется в зависимости от числа Рейнольдса Re и от эквивалентной абсолютной шероховатости Δэ. Для удобства сводные данные по определению λ представлены в таблице 4.1.
Пользоваться приведенными в табл. 4.1 формулами для определения коэффициента λ не всегда удобно. Для облегчения расчетов можно воспользоваться номограммой Колбрука-Уайта (рис.4.8), при помощи которой по известным Re и Δэ/ d весьма просто определяется λ.
Все гидравлические потери энергии делятся на два типа: потери на трение по длине трубопроводов (рассмотрены в п.4.3 и 4.4) и местные потери, вызванные такими элементами трубопроводов, в которых вследствие изменения размеров или конфигурации русла происходит изменение скорости потока, отрыв потока от стенок русла и возникновение вихреобразования.
Простейшие местные гидравлические сопротивления можно разделить на расширения, сужения и повороты русла, каждое из которых может быть внезапным или постепенным. Более сложные случаи местного сопротивления представляют собой соединения или комбинации перечисленных простейших сопротивлений.
Рассмотрим простейшие местные сопротивления при турбулентном режиме течения в трубе.
1. Внезапное расширение русла. Потеря напора (энергии) при внезапном расширении русла расходуется на вихреобразование, связанное с отрывом потока от стенок, т.е. на поддержание вращательного непрерывного движения жидких масс с постоянным их обновлением.
Это выражение является следствием теоремы Борда, которая гласит, что потеря напора при внезапном расширении русла равна скоростному напору, определенному по разности скоростей
2. Постепенное расширение русла. Постепенно расширяющаяся труба называется диффузором (рис.4.10). Течение скорости в диффузоре сопровождается ее уменьшением и увеличением давления, а следовательно, преобразованием кинетической энергии жидкости в энергию давления. В диффузоре, так же как и при внезапном расширении русла, происходит отрыв основного потока от стенки и вихреобразования. Интенсивность этих явлений возрастает с увеличением угла расширения диффузора α.
Кроме того, в диффузоре имеются и обычные потери на терние, подобные тем, которые возникают в трубах постоянного сечения. Полную потерю напора в диффузоре рассматривают как сумму двух слагаемых:
Учитывая это полную потерю напора можно переписать в виде:
откуда коэффициент сопротивления диффузора можно выразить формулой
Функция ζ = f(α)имеет минимум при некотором наивыгоднейшем оптимальном значении угла α, оптимальное значение которого определится следующим выражением:
При подстановке в эту формулу λТ =0,015…0,025 и n = 2…4 получим αопт = 6 (рис.4.11).
3. Внезапное сужение русла. В этом случае потеря напора обусловлена трением потока при входе в более узкую трубу и потерями на вихреобразование, которые образуются в кольцевом пространстве вокруг суженой части потока (рис.4.12).
Полная потеря напора определится по формуле ;
где коэффициент сопротивления сужения определяется по полуэмпирической формуле И.Е. Идельчика:
При выходе трубы из резервуара больших размеров, когда можно считать, что S2/S1 = 0, а также при отсутствии закругления входного угла, коэффициент сопротивления ζсуж = 0,5.
4. Постепенное сужение русла. Данное местное сопротивление представляет собой коническую сходящуюся трубу, которая называется конфузором (рис.4.13). Течение жидкости в конфузоре сопровождается увеличением скорости и падением давления. В конфузоре имеются лишь потери на трение
где коэффициент сопротивления конфузора определяется по формуле
Небольшое вихреобразование и отрыв потока от стенки с одновременным сжатием потока возникает лишь на выходе из конфузора в месте соединения конической трубы с цилиндрической. Закруглением входного угла можно значительно уменьшить потерю напора при входе в трубу. Конфузор с плавно сопряженными цилиндрическими и коническими частями называется соплом (рис.4.14).
5. Внезапный поворот трубы (колено). Данный вид местного сопротивления (рис.4.15) вызывает значительные потери энергии, т.к. в нем происходят отрыв потока и вихреобразования, причем потери тем больше, чем больше угол δ. Потерю напора рассчитывают по формуле
6. Постепенный поворот трубы (закругленное колено или отвод). Плавность поворота значительно уменьшает интенсивность вихреобразования, а следовательно, и сопротивление отвода по сравнению с коленом. Это уменьшение тем больше, чем больше относительный радиус кривизны отвода R / d рис.4.17). Коэффициент сопротивления отвода ζотв зависит от отношения R / d, угла δ, а также формы поперечного сечения трубы.
Для отводов круглого сечения с углом δ= 90 и R/d 
1 при турбулентном течении можно воспользоваться эмпирической формулой:
Все выше изложенное относится к турбулентному движению жидкости. При ламинарном движении местные сопротивления играют малую роль при определении общего сопротивления трубопровода. Кроме этого закон сопротивления при ламинарном режиме является более сложным и исследован в меньшей степени.