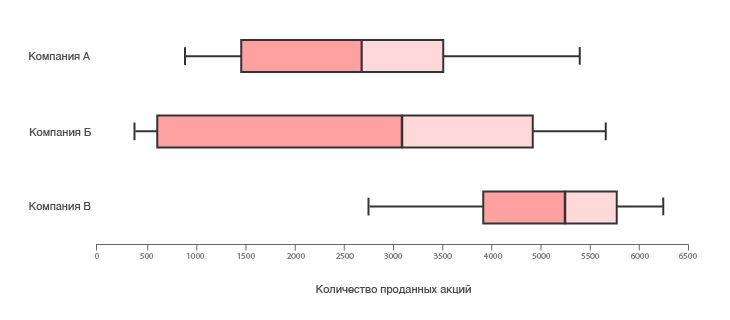
диаграмма размаха что показывает
Диаграмма «ящик с усами» (boxplot) в Excel 2016
Excel 2016, как известно, обогатился новыми типами диаграмм. Одна такая, которая диаграмма Парето, уже была показана. В этот раз рассмотрим другую, чисто статистическую. Называется «ящик с усами» или «коробчатая диаграмма» (box-and-whiskers plot или boxplot).
Раньше я такие видел только в специализированных ПО, типа STATISTICA, и для того, чтобы нарисовать подобную диаграмму в Excel, нужно было изрядно потрудиться. Теперь она есть в стандартном наборе Excel.
Зачем нужна такая диаграмма? Допустим, есть выборка для анализа. А еще лучше несколько выборок, которые нужно сравнить. Для этого рассчитывают различные показатели. Однако к любому расчету всегда хочется добавить наглядности, чтобы мозг перешел в режим образного представления, а не довольствовался сухими цифрами и формулами. Поэтому основные характеристики ловко изображают на рисунке. Отличным вариантом будет как раз диаграмма «ящик с усами».
На рисунке показан формат по умолчанию. Как видно, сравниваются две выборки путем изображения двух «ящиков с усами».
Что здесь что обозначает?
Крестик посередине – это среднее арифметическое по выборке.
Линия чуть выше или ниже крестика – медиана.
Нижняя и верхняя грань прямоугольника (типа ящика) соответствует первому и третьему квартилю (значениям, отделяющим ¼ и ¾ выборки). Расстояние между 1-м и 3-м квартилем – это межквартильный размах (или расстояние).
Горизонтальные черточки на конце «усов» – максимальное и минимальное значение (без учета выбросов, см. ниже).
Отдельные точки – это выбросы, которые показываются по умолчанию. Если значение выходит за пределы 1,5 межквартильных размаха от ближайшего квартиля, то оно считается аномальным. Их можно скрыть (см. ниже настройки).
Во всей красе «ящик с усами» проявляется при сравнении выборок, в которых данные делятся на категории. Допустим, провели некоторый эксперимент среди мужчин и женщин. Есть данные до и после эксперимента по обоим полам. Для анализа потребуется вычислить различные показатели. А если к этому добавить диаграмму «ящик с усами», то результат будет весьма наглядным.
Отлично видно, что после проведения эксперимента данные по мужчинам в целом уменьшились, а данные среди женщин наоборот, увеличились. Это не значит, что выборки больше не нужно анализировать (сравнивать, проверять гипотезы и т.д.). Но наглядность сильно улучшает понимание. Перейдем к настройкам.
Настройки диаграммы «ящик с усами»
Общий вид диаграммы настраивается стандартно. Можно менять цвет, добавлять подписи и т.д. Для этого есть две контекстные вкладки на ленте (Конструктор и Формат). Но есть настройки, предназначенные специально для этой диаграммы.
Выбираем какой-либо ряд и жмем Ctrl+1. Либо два раза кликаем по какому-нибудь «ящику». Можно через правую кнопку Формат ряда данных…. Справа вылазит панель настроек.
Рассмотрим по порядку.
Боковой зазор – регулирует ширину ящиков и расстояние между ними.
Показывать внутренние точки. Если поставить галочку, то на оси, где расположены «усы», точками будут показаны все значения. Так хорошо видно распределение внутри групп.
Показывать точки выбросов – отражать экстремальные значения.
Выбросы – это точки, выходящие за пределы 1,5 межквартильных размаха.
Показать средние метки – среднее арифметическое (крестики). Стоят по умолчанию, но можно скрыть.
Показать среднюю линию – только для различных категорий. Показывает изменения по категориям.
Если добавить линии, то изменения после эксперимента станут видны еще лучше. В справке написано, что соединяются медианы, но на графике почему-то соединяются средние. Чудеса.
Своевременное использование диаграммы «ящик-усы» может дать весьма ценную и наглядную информацию. Аналитику, который использует специализированные программы или трудоемкие настройки Excel, будет очень приятно иметь такую диаграмму под рукой.
Как показано в ролике ниже, все делается очень быстро и просто.
Ящики, усы и скрипки
Очень часто данные необходимо сравнивать. Например, у нас есть несколько рядов данных из какой-то области деятельности человека (промышленности, медицины, государственного управления, …), и мы хотим сравнить, насколько они похожи или, наоборот, чем одни показатели выделяются по сравнению с другими. Для простоты восприятия возьмем данные более простые, универсальные и нейтральные — высоту в холке и вес нескольких пород собак по сведениям Американского клуба собаководства (American Kennel Club). Данные по размерам пород в среднем можно найти здесь. Прибавим к ним функцию random.uniform из Python-библиотеки numpy, переведем дюймы в сантиметры, а фунты в килограммы, и вот мы получаем реалистично выглядящий набор данных по размерам собак нескольких пород, с которым можно работать. В нашем примере это чихуахуа, бигли, ротвейлеры и английские сеттеры.
Одну из аналитик, которую можно применить для сравнения этих 4 числовых рядов – посмотреть на их медиану. Она разбивает ряд данных на две части: половина значений меньше медианы и остальная половина – больше. Медианные значения находим, группируя с помощью библиотеки pandas по столбцу «Порода» и применяя к сгруппированным данным функцию median. Аналогично можно было бы посмотреть и другие статистические показатели: среднее значение (mean) и моду (mode).
Видим, что половина встреченных нами чихуахуа имеет высоту в холке не больше 18 см, бигль значительно выше – в районе 41 см, и следующие по размерам – ротвейлер и английский сеттер, которые отличаются по росту незначительно: 58 и 63 см.
Рисунок 2. Медианные значения высоты в холке четырех пород собак.
Но только одной медианы недостаточно для сравнительного анализа данных. Можно получить больше информации, если рассмотреть такой инструмент как диаграмма размаха (также известная как «ящик с усами», box-and-whiskers plot), построенную с помощью Python-библиотеки для построения графиков seaborn. Линия внутри ящика – это уже знакомая нам медиана. Ее уровень на графике справа (см. Рисунок 3) совпадает с высотой соответствующего столбца слева. Но при этом диаграмма размаха содержит дополнительную информацию о том, как данные распределены внутри ряда: нижняя граница прямоугольника (ящика) – это первый квартиль (величина, превосходящая 25% значений ряда), а верхняя граница – третий квартиль (величина, превосходящая 75% значений). А те самые «усы» — отрезки, отходящие вверх и вниз от середины прямоугольника – строятся на основе интерквартильного размаха и обозначают верхнюю и нижнюю границу значимой части наших данных, исключая выбросы. Здесь выбросы отсутствуют (дистрофиков и собак-гигантов нам в рассмотрение не попадалось), при наличии они отобразились бы метками за пределами «усов».
Рисунок 3. Сравнение столбчатой и диаграммы размаха, построенных для одного и того же набора данных.
Скрипичный график (violinplot) из той же библиотеки seaborn дает нам еще больше информации о структуре рассматриваемых данных. Ниже на Рисунке 4 представлены все три графика, где породы идут каждый раз в одинаковом порядке, а цвет для соответствующего ряда сохраняется.
Рисунок 4. Сравнение столбчатой диаграммы, диаграммы размаха и скрипичного графика, построенных для одного и того же набора данных.
Например, зеленым показаны данные о ротвейлерах.
Сходства и различия диаграммы размаха (ящика с усами) и скрипичного графика показаны на следующем Рисунке 5. Сначала сходства: (1) оба графика в том или ином виде отражают 0.25-квантиль, 0.5-квантиль (медиану) и 0.75-квантиль; (2) и там, и там отражаются крайние значения, которые близки к величине полутора межквартильных интервалов (IQR), отложенных от нижнего и верхнего края коробки – те самые «усы» для диаграммы размаха, за пределами которых находятся «выбросы».
Отличие же состоит в том, что скрипичный график содержит также информацию о том, как данные распределены внутри, т.к. границы построенной «скрипки» — это повернутая на 90 градусов плотность распределения. И в этом случае при анализе графика у нас гораздо больше информации: в дополнение к квантилям и значениям, описывающим 4 интерквартильных расстояния (1.5 + 1 + 1.5) на скрипичном графике можно увидеть, распределены ли данные равномерно или есть несколько центров, где значения встречаются более часто.
Рисунок5. Пояснения по соответствию элементов двух графиков: размаха и скрипичного.
Более ярко эту мысль можно увидеть на следующем графике (Рисунок 6), где данные по двум группам ротвейлеров отличаются, но подобраны таким образом, что медианы совпадают (крайний слева график) и даже больше – диаграммы размаха (в центре) тоже совпадают! И только скрипичный график (крайний справа) показывает нам, что на самом деле структура данных значительно отличается.
Рисунок 6. Пример, когда только скрипичные график позволяет нам увидеть отличия во внутренней структуре рассматриваемых данных.
Используя кластеризацию К-средних (cluster.KMeans) из модуля sklearn, мы можем визуально представить сгруппированные данные, построив диаграмму разброса с помощью функции scatterplot модуля seaborn. Здесь цвет отделяет один кластер, созданный ML-алгоритмом, от другого, а форма маркера показывает исходную принадлежность к той или иной группе. Понижать размерность с помощью PCA или какого-либо другого метода здесь было не нужно, т.к. данные изначально 2D.
Код для кластеризации и построения диаграммы разброса:

Таким образом, на примере данных о высоте в холке нескольких пород собак мы познакомились с некоторыми статистическими характеристиками числовых рядов и инструментах их визуализации. Простой инструмент дает понятную метрику, но не дает полной картины. Более сложные инструменты дают более глубокую картину данных, но и воспринимаются также сложнее в силу увеличения количества информации на графике. И здесь важно выбирать инструмент под конкретную задачу, чтобы находить баланс между требующейся полнотой информации и простотой ее восприятия на графике.
Как сравнивать данные с помощью усов, ящиков и скрипок?
Для простоты восприятия возьмем данные более простые, универсальные и нейтральные — высоту в холке и вес нескольких пород собак по сведениям Американского клуба собаководства (American Kennel Club). Данные по размерам пород в среднем можно найти здесь. Прибавим к ним функцию random.uniform из Python-библиотеки numpy, переведем дюймы в сантиметры, а фунты в килограммы, и вот мы получаем реалистично выглядящий набор данных по размерам собак нескольких пород, с которым можно работать. В нашем примере это чихуахуа, бигли, ротвейлеры и английские сеттеры.
Одну из аналитик, которую можно применить для сравнения этих 4 числовых рядов – посмотреть на их медиану. Она разбивает ряд данных на две части: половина значений меньше медианы и остальная половина – больше. Медианные значения находим, группируя с помощью библиотеки pandas по столбцу «Порода» и применяя к сгруппированным данным функцию median. Аналогично можно было бы посмотреть и другие статистические показатели: среднее значение (mean) и моду (mode).
Видим, что половина встреченных нами чихуахуа имеет высоту в холке не больше 18 см, бигль значительно выше – в районе 41 см, и следующие по размерам – ротвейлер и английский сеттер, которые отличаются по росту незначительно: 58 и 63 см.
Но только одной медианы недостаточно для сравнительного анализа данных. Можно получить больше информации, если рассмотреть такой инструмент как диаграмма размаха (также известная как «ящик с усами», box-and-whiskers plot), построенную с помощью Python-библиотеки для построения графиков seaborn. Линия внутри ящика – это уже знакомая нам медиана. Ее уровень на графике справа (см. Рисунок 3) совпадает с высотой соответствующего столбца слева.
Но при этом диаграмма размаха содержит дополнительную информацию о том, как данные распределены внутри ряда: нижняя граница прямоугольника (ящика) – это первый квартиль (величина, превосходящая 25% значений ряда), а верхняя граница – третий квартиль (величина, превосходящая 75% значений).
А те самые «усы» — отрезки, отходящие вверх и вниз от середины прямоугольника – строятся на основе интерквартильного размаха и обозначают верхнюю и нижнюю границу значимой части наших данных, исключая выбросы. Здесь выбросы отсутствуют (дистрофиков и собак-гигантов нам в рассмотрение не попадалось), при наличии они отобразились бы метками за пределами «усов».
Скрипичный график (violinplot) из той же библиотеки seaborn дает нам еще больше информации о структуре рассматриваемых данных. Ниже на Рисунке 4 представлены все три графика, где породы идут каждый раз в одинаковом порядке, а цвет для соответствующего ряда сохраняется.
Например, зеленым показаны данные о ротвейлерах.
Сходства и различия диаграммы размаха (ящика с усами) и скрипичного графика показаны на следующем Рисунке 5. Сначала сходства: (1) оба графика в том или ином виде отражают 0.25-квантиль, 0.5-квантиль (медиану) и 0.75-квантиль; (2) и там, и там отражаются крайние значения, которые близки к величине полутора межквартильных интервалов (IQR), отложенных от нижнего и верхнего края коробки – те самые «усы» для диаграммы размаха, за пределами которых находятся «выбросы».
Отличие же состоит в том, что скрипичный график содержит также информацию о том, как данные распределены внутри, т.к. границы построенной «скрипки» — это повернутая на 90 градусов плотность распределения. И в этом случае при анализе графика у нас гораздо больше информации: в дополнение к квантилям и значениям, описывающим 4 интерквартильных расстояния (1.5 + 1 + 1.5) на скрипичном графике можно увидеть, распределены ли данные равномерно или есть несколько центров, где значения встречаются более часто.
Более ярко эту мысль можно увидеть на следующем графике (Рисунок 6), где данные по двум группам ротвейлеров отличаются, но подобраны таким образом, что медианы совпадают (крайний слева график) и даже больше – диаграммы размаха (в центре) тоже совпадают! И только скрипичный график (крайний справа) показывает нам, что на самом деле структура данных значительно отличается.
Используя кластеризацию К-средних (cluster.KMeans) из модуля sklearn, мы можем визуально представить сгруппированные данные, построив диаграмму разброса с помощью функции scatterplot модуля seaborn. Здесь цвет отделяет один кластер, созданный ML-алгоритмом, от другого, а форма маркера показывает исходную принадлежность к той или иной группе. Понижать размерность с помощью PCA или какого-либо другого метода здесь было не нужно, т.к. данные изначально 2D.
Код для кластеризации и построения диаграммы разброса:
Таким образом, на примере данных о высоте в холке нескольких пород собак мы познакомились с некоторыми статистическими характеристиками числовых рядов и инструментах их визуализации. Простой инструмент дает понятную метрику, но не дает полной картины. Более сложные инструменты дают более глубокую картину данных, но и воспринимаются также сложнее в силу увеличения количества информации на графике. И здесь важно выбирать инструмент под конкретную задачу, чтобы находить баланс между требующейся полнотой информации и простотой ее восприятия на графике.
Первым делом хочу попросить прощения у всех граждан России. Благодаря моим действиям, описанным вкратце в этой статье, я получил некоторую сумму денег, которая иначе могла бы попасть в бюджет РФ. Но произошло это по вине сотрудников АО «Почта России». Учредителем и единственным акционером АО «Почта России» является Российская Федерация.
Диаграмма размаха («ящик с усами»)
Описание
Диаграммы размаха («ящик с усами») (Box and Whisker Plot или Box Plot) – это удобный способ визуального представления групп числовых данных через квартили.
Прямые линии, исходящие из ящика, называются «усами» и используются для обозначения степени разброса (дисперсии) за пределами верхнего и нижнего квартилей. Выбросы иногда отображаются в виде отдельных точек, находящихся на одной линии с усами. Диаграммы размаха могут располагаться как горизонтально, так и вертикально.
Диаграммы размаха, как правило, используются в описательной статистике и позволяют быстро исследовать один или более наборов данных в графическом виде. Несмотря на то, что в сравнении с гистограммой или графиком плотности, этот график может показаться примитивным, его преимущество – в экономии пространства, что особенно удобно при сравнении распределений между большим количеством групп или наборов данных.
Виды наблюдений, которые можно сделать на основе ящика с усами:
Каковы ключевые значения, например: средний показатель, медиана 25го перцентиля и так далее.
Существуют ли выбросы и каковы их значения.
Симметричны ли данные.
Насколько плотно сгруппированы данные.
Смещены ли данные и, если да, то в каком направлении.
Два из наиболее распространенных варианта ящика с усами – диаграмма размаха с переменной шириной и диаграмма размаха с метками.
Диаграмма размаха что показывает
Уважаемые посетители Портала Знаний, если Вы найдете ошибку в тексте, выделите, пожалуйста, ее мышью и нажмите Сtrl+Enter. Мы обязательно исправим текст!
Диаграмма размаха
Вид графического отображения данных, когда диапазоны или характеристики распределения значений переменной изображаются отдельно для групп наблюдений, заданных значениями другой, категориальной (группирующей), переменной.
Для каждой группы вычисляется статистика центра (медиана или среднее) и статистики диапазона (например, квартили или стандартные отклонения), и выбранные значения изображаются на диаграмме размаха.
Также могут быть изображены точки выбросов (outliers).
Визуально анализируя диаграмму размаха, можно получить представление об изменчивости переменной. На данной диаграмме размаха отмечены три выброса – два «слишком больших» значения и одно «слишком маленькое».
Например, значение Тромбоциты = 73 оказывается выбросом для группы мужчин, но при рассмотрении группы женщин это наблюдение оказывается «нормальным».
Сравнение групп, изображенных на диаграмме размаха, производится с помощью критериев парных сравнений (t-критерий, критерий Манна-Уитни и др.) в случае двух групп, и с помощью дисперсионного анализа (ANOVA) или введения поправки Бонферрони в случае нескольких (более двух) групп.