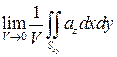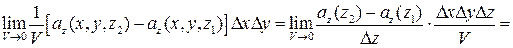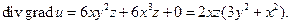дивергенция радиус вектора чему равна

Основные операции векторного анализа в криволинейных координатах

Содержание:

По этой ссылке вы найдёте полный курс лекций по математике:

Дифференциальные уравнения векторных линий Рассмотрим поле вектора Уравнения векторных линий в криволинейных координатах q\, q2i g3 имеют вид В цилиндрических координатах в сферических координатах 14.2. Градиент в ортогональных координатах Пусть скалярное поле. Тогда Основные операции векторного анализа в криволинейных координатах Дифференциальные уравнения векторных линий радиент в ортогональных координатах Ротор в ортогональных координатах Дивергенция в ортогональных координатах.

Вычисление потенциала в криволинейных координатах Линейный интеграл и циркуляция в ортогональных криволинейных координатах Оператор Лапласа в ортогональных координатах В цилиндрических координатах в сферических координатах 14.3. Ротор в ортогональных координатах Рассмотрим векгорное поле и вычислим rot а. Имеем В цилиндрических координатах в сферических координатах 14.4. Дивергенция в ортогональных координатах Дивергенция div а векторного поля вычисляется по формуле.

В цилиндрических координатах или в сферических координатах

Отсюда следует, что Интегрируя систему дифференциальных уравнений с частными производными (9), найдем искомый потенциал произвольная постоянная. В цилиндрических координатах система (9) принимает вид В сферических координатах система (9) имеет вид Пример 2. Найти потенциал векторного поля, заданного в цилиндрических координа тех Убедимся, что По формуле (5) л о лучим данное поле потенциально.

Возможно вам будут полезны данные страницы:

Дифференцируя это соотношение no z и используя тре тье уравнение, получим Линейный интеграл и циркуляция в ортогональных криволинейных координатах Пусть векторное поле определено и непрерывно в области Q изменения ортогональных криволинейных координат 4i, 42, 4з • Так как дифференциал радиус-вектора г любой точки M(qb 42, 43) G П выражается формулой то криволинейный интеграл вектора а(М) по ориентированной гладкой или кусочно-гладкой кривой L СП будет равен В частности, для цилиндрических координат ) будем иметь.

Отсюда по формуле (13) получим Аналогично для сферических координат будем иметь Отсюда по формуле (13) получим Основные операции векторного анализа в криволинейных координатах Дифференциальные уравнения векторных линий радиент в ортогональных координатах Ротор в ортогональных координатах Дивергенция в ортогональных координатах.

Вычисление потенциала в криволинейных координатах Линейный интеграл и циркуляция в ортогональных криволинейных координатах.

Оператор Лапласа в ортогональных координатах Если кривая L замкнута (начальная и конечная точки кривой L совпадают), то циркуляция Ц векторного поля а(М) в криволинейных координатах 4,, q2, 43 вычисляется по формуле (13), а в случае цилиндрических или сферических координат — по формулам (14) или (15) соответственно. Пример 3. Вычислить циркуляцию векторного поля, заданного в цилиндрических координатах по замкнутой кривой L, Координаты данного вектора равны соответственно Контур L представляет собой замкнутую кривую, расположенную в плоскости z = 0 (рис. 43).

Так как искомое решение и должно зависеть только от расстояния точки М от начала координат г, т., то уравнение Лапласа Ди = 0 в сферических координатах будет иметь вид Отсюда так что где постоянные. Упражнения Найдите производную скалярного поля в точке по направлению кточке Найдите производную скалярного поля и(х, у, z) в точке Л#о(хо, Уо» *о) по направлению нормали к поверхности S, образующей острый угол с положительным направлением оси О г: 6.

Найдите производную скалярного поля в точке эллипса + = 1 по направлению внешней нормали к эллипсу в этой точке. 7. Найдите производную скалярного поля в точке по направлению окружности 8. Найдигеугол между градиентами функции и = arctg | в точках 9. Найдите производную плоского поля и вточке понаправле-нию, задаваемому вектором, лежащим в плоскости хОу и наклоненным под углом | коси Ох. Найдите векторные линии следующих векторных полей: 13.

Дивергенция в ортогональных координатах

Достраивая подходящим образом заданные незамкнутые поверхности до замкнутых и пользуясь теоремой Гаусса—Остроградского, вычислите потоки векторных полей через указанные поверхности (к замкнутой поверхности берем внешнюю нормаль): Найдите работу силы F при перемещении вдольлинии L от точки М к точке N: Найдите циркуляцию векторного поля а вдоль замкнутого контура L (в направлении, соответствующем возрастанию параметра Вычислите циркуляцию векторного поля а по замкнутому контуру L.

Присылайте задания в любое время дня и ночи в ➔

Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.

Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.

Источник

Дивергенция векторного поля

Особый интерес представляет случай, когда вычисляется поток через замкнутую поверхность. Обычно в таких случаях за положительную сторону поверхности принимают ее внешнюю поверхность. Поверхностный интеграл в этом случае обозначается следующим образом:

.

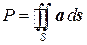
Когда векторное поле a представляет собой поле скоростей жидкости, величина потока P дает разность между количеством жидкости, вытекающей из внутренней области, ограниченной поверхностью S, и количеством, втекающей в эту область. Если P=0, то во внутреннюю область втекает столько же жидкости, сколько и вытекает. Если же P>0, то вытекает больше, чем втекает. Это означает, что внутри области имеются источники, питающие поток жидкости. В случае электрического поля, это означает, что внутри области находятся электрические заряды. Если P

.

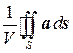
Найдем теперь предел этого отношения, при условии что область, ограниченная поверхностью S, стягивается в точку M, т.е. при V®0. Этот предел называется дивергенцией векторного поля a в точке M:

. (6.5)

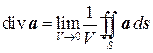
Ясно, что если предел существует, то он не зависит от формы поверхности S.

Дивергенция характеризует мощность источника или стока. Например, если в каждой точке поля скоростей жидкости дивергенция равна нулю, то это означает не только отсутствие источников и стоков, но и то, что жидкость не сжимается и не расширяется. Этим свойством, в частности, обладает воздух при скоростях, не превышающих примерно половины скорости звука. Однако при скоростях близких или превосходящих скорость звука, воздух ведет себя как сжимаемый газ. Тогда дивергенция такого газа будет уже отлична от нуля. Точно также дивергенция отлична от нуля, если в текущем газе возникают химические реакции (например, горение), изменяющие его плотность. В случае гравитационных или электрических полей дивергенция будет пропорциональна плотности масс или зарядов, соответственно.

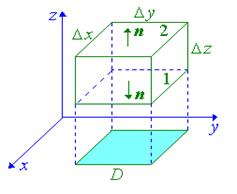
Выведем теперь формулу для дивергенции в декартовой системе координат. Пусть поверхность S имеет вид прямоугольного параллелепипеда со сторонами Dx, Dy, Dz, параллельного координатным осям (см. рис.6.6). Распишем поверхностный интеграл в определении дивергенции в виде суммы трех двойных интегралов:

. (6.6)

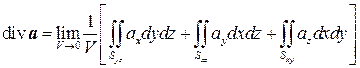
Рис. 6.6

Рассмотрим третье слагаемое:

Грани 1 и 2 проецируются в одну и ту же область D на плоскости xOy (боковые грани можно не учитывать, т.к. они перпендикулярны плоскости xOy), однако их внешние нормали направлены в противоположные стороны. Считая, что уравнения граней z=z₁ и z=z₂, получим

.

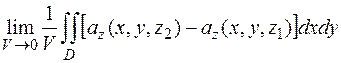
Исходя из геометрического смысла двойного интеграла (это есть объем находящийся между координатной плоскостью и поверхностью, описываемой подынтегральной функцией):

.

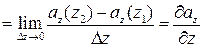
Аналогично можно получить формулы для первого и второго слагаемого в выражении

, .

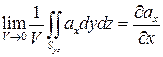
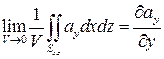
Таким образом, мы доказали следующую теорему:

Теорема. В декартовой системе координат дивергенция векторного поля a = a_xi+a_yj+a_zk вычисляется по формуле:

. (6.7)

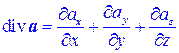
1) Пусть дано однородное поле:a = Ai+Bj+Ck, где A, B, C – постоянные величины. Тогда

div a = 0.

Это означает, что если все части жидкости имеют одну и ту же скорость (т.е. жидкость движется поступательно, как твердое тело), то в таком потоке не может быть ни источников, ни стоков.

2) Пусть твердое тело вращается с постоянной угловой скоростью w. Как известно из теоретической механики линейная скорость равна v=w´r, где r – радиус-вектор точки относительно точки вращения. Если неподвижную точку взять в качестве начала координат, а ось Oz направить вдоль оси вращения, то получим w=wk, r=xi+yj+zk. Тогда

v = –wyi + wxj. (6.8)

Это есть поле линейных скоростей вращающегося твердого тела. Вычислим дивергенцию этого поля:

.

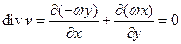
Это означает, что есть представить себе жидкость, вращающейся как твердое тело, то в таком потоке не может быть ни стоков, ни источников.

Пример 6.4. Найти дивергенцию градиента скалярного поля u=x 3 y 2 z в точке M(1;–1;1).

Решение. Найдем градиент поля

,

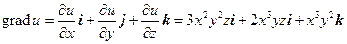
а затем дивергенцию:

Подставляя координаты точки M, получим

.

Источник

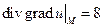
Дивергенция радиус вектора чему равна

Библиографическая ссылка на статью:
Чуев А.С. О понятии дивергенции поля векторных физических величин // Современные научные исследования и инновации. 2013. № 1 [Электронный ресурс]. URL: https://web.snauka.ru/issues/2013/01/20234 (дата обращения: 03.12.2021).

Истина бытия – это сущность,

истина сущности есть понятие.

ВВЕДЕНИЕ

Понятие «дивергенция» переводится на русский язык как расходимость (можно к этому отнести и сходимость) линий векторного поля. Логически это понятно, в пространственно неоднородном векторном поле (когда есть изменение плотности линий поля) дивергенция не нулевая. В однородном векторном поле дивергенция равна нулю.

На практике, если брать математическое определение дивергенции, то ненулевое значение дивергенции приписывается исключительно только в истоках и стоках поля без определенности их размера. Например, для центральных полей типа электрического и гравитационного, дивергенция считается равной нулю всюду, кроме истоков и стоков. Если же брать в качестве примера магнитное поле, то равенство нулю дивергенции вектора магнитной индукции B вообще возведено в закон (четвертое уравнение Максвелла).

Автор считает, что с точки зрения логики и здравого физического смысла дивергенция в любой точке векторного поля – это скорость пространственного изменения вектора в своем собственном направлении (изменение модуля), а смысл ротора – скорость пространственного изменения направления вектора. Поскольку выделенная в тексте позиция не соответствует общепринятой точке зрения, попробуем пояснить и защитить ее, привлекая наглядные изображения векторных полей, логику понятий и математический аппарат.

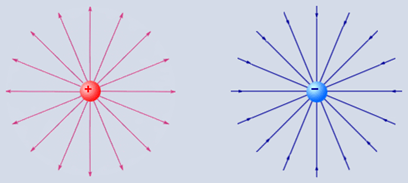
Хорошо известны изображения расходящихся и сходящихся силовых линий полей центрального типа (рис.1) и вихреобразных силовых линий стержневого магнита (рис.2). Силовые линии поля строятся по касательным, определяющим направление силы в любой точке пространства, окружающего электрический заряд или магнит.

Рис.1 Пространственная расходимость и сходимость линий электрического поля

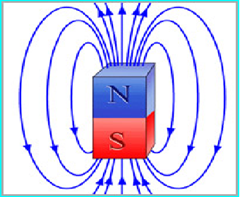
Рис.2. Пространственная расходимость и сходимость силовых линий магнитного поля

Известно, что густота силовых линий определяет числовое значение вектора в любой точке поля, а его направление определяется по касательной к линии в этой точке.

По рис.1, хотя пространственная расходимость и сходимость силовых линий электрического поля очевидны и густота линий убывает при отдалении от центра, дивергенция таких полей (центрального типа) всюду вне источника или стока считается равной нулю.

По рис.2 ситуация сложнее. Считается, что источников магнитного поля нет и линии поля замкнуты сами на себя. В соответствии с четвертым уравнением Максвелла дивергенция силового вектора магнитной индукции B всюду равна нулю. Однако приводимая картина наглядно иллюстрирует, что значение индукции B, определяемое густотой линий, вблизи торцов магнита максимально большое, а в отдалении оно становится меньше. На бесконечно большом удалении от магнита значение магнитной индукции будет нулевым. Таким образом можем констатировать, что в окружающем магнит пространстве тоже имеет место изменение модуля вектора B – это эмпирический факт.

Но если есть изменение модуля вектора (хотя сам поток не изменяется 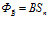), то неизбежно будет и дивергенция вектора (или поля, если дивергенцию понимать как пространственную расходимость или сходимость линий поля). Поэтому утверждение четвертого уравнения Максвелла о равенстве нулю дивергенции вектора B в любой точке магнитного поля применительно к рис.2, со всей очевидностью, – ложно.

Несмотря на очевидность приводимых фактов, известных почти каждому, в физике почему-то общепринято и не подвергается сомнению известное положение о нулевом значении дивергенции векторных полей вне источников и стоков поля 2. Заблуждение это, по мнению автора, частью связано с гидродинамической аналогией, а частью с привычкой упрощенного описания центральных полей в сферической системе координат.

Приведем конкретные примеры из классических учебников с имеющейся там трактовкой понятия дивергенции. Возьмем классический учебник Тамма И.Е. «Основы теории электричества» [1, стр.586]. Тамм пишет: «Отметим в заключение, что в гидродинамике дивергенция скорости жидкости v имеет непосредственное физическое значение. Действительно, в каждой точке жидкости

при (1)

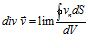
Слова сила или обильность истоков и стоков поля здесь применены правильно, они очень хорошо подходят в качестве характеристики для источников и стоков поля. Но причем тут дивергенция (расходимость) поля?

Другой источник, более современный, описывая дивергенцию конкретного электрического поля [2, стр.24], излагает так: «В дифференциальной форме теорема Гаусса является локальной теоремой: дивергенция поля Е в данной точке зависит только от плотности электрического заряда ρ в этой точке и больше ни от чего. Это одно из замечательных свойств электрического поля. Например, в разных точках поля точечного заряда поле Е отличается друг от друга. Это же относится, вообще говоря, и к пространственным производным , , . Однако, как утверждает теорема Гаусса, сумма этих производных, которая определяет дивергенцию Е, оказывается во всех точках поля (вне самого заряда) равной нулю».

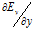
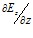
В этой фразе чувствуются сильные нотки сомнения в излагаемом материале, но они прикрыты ссылкой на авторитет теоремы Гаусса. Но вообще-то защищать позицию, при которой производные по координатам есть, а их сумма всегда равна нулю – это против здравого смысла. Ведь пространственные изменения по трем координатам вполне могут быть одного знака, а также изменение может быть только по одной координате. В последнем случае вообще некуда деваться, ведь при изменении вектора по одной единственной координате, совпадающей с направлением вектора, как ни крути, а придется признавать наличие ненулевой дивергенции.

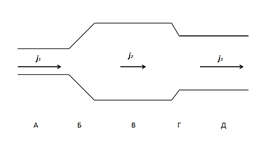
Наглядная иллюстрация к этому случаю приведена на рис.3. Здесь изображено изменение плотности электрического тока в линейном однородном проводнике переменного сечения. Очевидно, что на участках Б и Г, где происходит переход от одного значения плотности тока к другому значению, 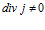. Аналогичный пример можно привести и для жидкости, текущей в линейной трубе переменного сечения. Для скоростного потока жидкости в трубе, как и для плотности тока, дивергенция потокового вектора в местах расширения и сужения трубы не будет равна нулю – это факт.

Рис.3. Изменение плотности тока в линейном проводнике переменного сечения

Если рассматривать потенциальное электрическое поле точечных зарядов (рис.1), то ситуация с критикуемым пониманием дивергенции вообще забавная. Вне заряда дивергенция признается равной нулю, а в самом заряде она неопределенна ввиду немыслимо большой плотности заряда. Тогда о каком значении дивергенции вообще можно вести речь?

Приведем еще один пример из зарубежных источников (заблуждение не знает границ) [3, стр.73]. Рассматривается электрическое поле, создаваемое заряженным источником в виде бесконечно длинного цилиндра. «Вне цилиндра, где нет заряда, конечный поток, вытекающий из любого объема – и большого и малого, – равен нулю, так что предел отношения потока к объему, конечно, равен нулю. Внутри цилиндра мы получили результат, следующий из фундаментального соотношения (54) (примеч. в ссылке div E = 4)».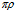

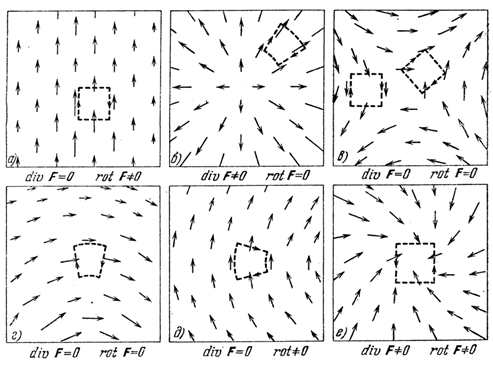
В этой же книге [3] приводится иллюстрация, изображенная на рис.4, позволяющая трактовать дивергенцию точно так же, как ее понимает автор настоящей статьи.

Выделенная область на рис. 4 б) не содержит источников и стоков, однако дивергенция поля в этой области не равна нулю и это правильно. Дивергенция есть в любой точке неоднородного поля, неоднородного в реальном трехмерном физическом пространстве. То есть в любой точке поля, где наблюдается расходимость или сходимость линий векторного поля.

Рис.4. Значения дивергенции и ротора в выделенной области векторного поля

Исходя из описываемого здесь понятия дивергенции, можно предположить, что в случае центрального электрического поля (берем вектор D в системе СИ), дивергенция в любой точке поля будет численно равняться объемной плотности заряда, приходящегося на объем шара с радиусом, равным удалению данной точки поля от центрального источника. В этом случае работают и теорема Гаусса и наше понимание дивергенции векторного поля.

Одним из оппонентов данной точки зрения на дивергенцию автору была высказана претензия в том, что он «придумал» свое определение дивергенции и не вправе пользоваться общепринятым. Помилуйте! Я ничего не придумывал и пользуюсь таким определением, как оно есть [4, стр. 358]. Дивергенцией называется функция

, (2)

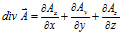
а то, что она входит в подынтегральное выражение формулы Остроградского

, (3)

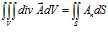
так эта формула, при допущении равномерной плотности потока, применима для поверхностей и объемов любого размера. При отсутствии такого допущения формулой (3) пользоваться практически невозможно.

Наше понимание дивергенции, как изменения вектора в своем собственном направлении, математически обоснована тем, что формула (2) обязательно дает нулевой результат только при неизменности модуля вектора 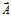. Это определяется свойством любого вектора – сохранять свое значение по модулю при любых поворотных изменениях системы координат. Заметим, прямо противоположное качество у функции ротора вектора.

Осознание ложности привязки понятия дивергенции лишь к источникам и стокам поля уже появилось в гидродинамике [5]. По мнению автора, не за горами признание аналогичного положения и в других областях физики, в частности, в электростатике и магнитостатике. Отмеченное соответствует математическому положению о том, что «всякое векторное поле А дает некоторое скалярное поле divA, а именно поле своей расходимости» [4, стр.359]. Если векторное поле непрерывно и дифференцируемо в своей области, то в той же области должно существовать и быть непрерывным скалярное поле его дивергенции.

при (4)

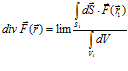
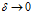
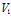
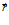
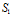
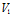
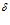
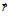
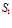
где: — область, содержащая точку (), — замкнутая поверхность, ограничивающая область , — наибольшее расстояние от точки () до точек поверхности .

В формуле (4) имеет место уход от устремления объема в точку, анализируются поверхность и объем, внутри которых расположена рассматриваемая точка поля. При правильной интерпретации этой формулы и применительно к полям центрального типа она дает результат, близкий к верному.

В источнике [8] для физических полей приводится еще одно, несколько иное, определение дивергенции. Здесь дивергенция определяется как показатель объемной плотности потока векторной величины в той или иной точке пространства векторного поля. Дивергенция в этом случае математически выражается так:

при (5)

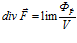
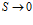
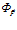
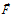
где: – поток векторного поля через сферическую поверхность площадью S, ограничивающую объем V. Считается, что такое определение дивергенции применимо не только к декартовым системам координат. Надо отметить, что здесь не очень понятно требование сферичности, а не замкнутости поверхности.

В чем-то аналогичный подход обнаруживается и в работе [9, стр.22]: «… дивергенция векторного поля а(М) является объемной плотностью потока векторного поля а(М) в данной точке М». По мнению автора, такой подход более близок к истине.

В источнике [8] приводится интересный пример наглядной физической модели дивергенции: «Например, если в качестве векторного поля взять совокупность направлений наискорейшего спуска на земной поверхности, то дивергенция покажет местоположение вершин и впадин, причём на вершинах дивергенция будет положительна (направления спуска расходятся от вершин), а на впадинах отрицательная (ко впадинам направления спуска сходятся)».

По мнению автора, такая модель дивергенции не совсем логична. На вершинах и впадинах наискорейшего спуска совсем нет, а в источниках или стоках дивергенция по модулю должна быть максимальна. Кроме того, данная модель, во-первых, исключает гладкость вершин и впадин, поскольку значения дивергенции скачут от плюса к минусу, а правило перехода не обозначено. Во-вторых, надо заметить, принимая пространственное направление за векторную величину, ее нельзя определять в том же пространстве направлений. Пример из логики: нельзя определить понятие через само это понятие, иначе получится тавтология.

В наглядных примерах по рис.1 и рис.2 видно, что дивергенция (расходимость) электрических и магнитных силовых линий есть и заведомо есть плавное уменьшение модуля вектора при отдалении рассматриваемых точек окружающего пространства от источника и стока поля. Для центральных полей вычислить дивергенцию как объемную плотность потока вектора в той или иной точке поля не сложно. Но для соленоидального магнитного поля определение дивергенции как объемной плотности потока векторного поля затруднительно, поскольку это поле не сферично. К тому же заметим, дивергенция, по сути, должна быть не плотностью потока векторного поля, что присуще и однородным векторным полям, а пространственным изменением плотности потока вектора в той или иной точке поля. Математически это можно выразить так:

при и (6)

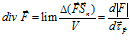
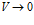
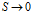
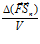
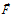
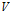
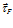
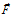
где: – изменение плотности потока векторной величины в рассматриваемом объеме предельно малого размера; – единичный вектор, касательный к направлению вектора в данной точке.

Кажется не вполне осознаваемое, но почти полное соответствие авторскому пониманию дивергенции удалось обнаружить в источнике [10, стр.206]: «Дивергенцию векторной функции … еще называют расходимостью. Она определяет скорость изменения каждой компоненты вектора в своем «собственном» направлении». Но если есть изменения компонентов вектора в своем «собственном направлении», то не замечать или отрицать такое же изменение самого вектора – просто грешно.

В заключение приведем и рассмотрим для сравнения в табличном формате различные варианты определения дивергенции, в том числе, предлагаемые автором и защищаемые им как наиболее подходящие (см. таблицу 1).

Таблица 1. Возможные определения и толкования дивергенции

Источник