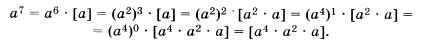для чего нужен инвариант цикла
Инвариант цикла
Программисты часто составляют циклы, как правило, чтобы достичь какой-то конкретной цели: найти элемент с заданными свойствами, выполнить сортировку и т. п. Но как убедиться в том, что цель будет достигнута, не выполняя цикл непосредственно? В этом нам поможет инвариант цикла.
Рассмотрим использование инварианта цикла на примере поиска индекса наименьшего элемента в целочисленном массиве.
Инвариант цикла будет выглядеть так:
Инициализируем переменные, входящие в инвариант, так, чтобы он был истинным до начала выполнения цикла:
Инвариант цикла && Условие_окончания_цикла => Цель цикла
Вместо условия окончания можно использовать условие выполнения цикла. В нашем случае это: nextToCheck (пока есть элементы для проверки). Как только оно будет нарушено (станет ложным), выполнение цикла прекратится
Таким образом, подобрав инвариант цикла и обеспечив его сохранение, мы можем гарантировать достижение цели, не выполняя сам цикл.
Вопросы для самопроверки при составлении циклов:
При составлении циклов может оказаться удобным понятие области неопределенности, используемое в вычислительных методах математики. Область изменения параметров задачи (в нашем примере: [0,n)) можно разделить на две части: исследованную область (для которой найден TemporarySmallest : [0,nextToCheck) ) и область неопределенности ( [nextToCheck,n) ). Необходимо составлять цикл так, чтобы на каждой итерации область неопределенности сокращалась.
Инвариант цикла будет таким:
Непосредственно перед циклом инициализируем значение numSorted :
что делает инвариант цикла истинным.
На каждой итерации количество numSorted увеличивается на единицу. Чтобы этого достичь, выбирается наименьший среди первых [0,n-numSorted) неотсортированных элементов, и меняется местами (с помощью функции swap() ) c элементом n-numSorted
Таким образом, отсортированный «хвост» массива всякий раз удлиняется на один элемент, а неотсортированная «голова» уменьшается.
Что почитать
Вирт Н. Алгоритмы + структуры данных = программы
Для чего нужен инвариант цикла
Начнем, как обычно, с задачки. В строке, содержащей цепочки одинаковых символов, нужно их обнаружить и заменить на счетчик повторений и один такой символ. Например, из строки « abcdddddddddefggggggggggggggggggx » получить « abc 9 def 18 gx ». Извечный вопрос русской интеллигенции: «Что делать?».
Типичный ход рассуждений: «Будем просматривать строку в цикле. Если обнаружим повторяющийся фрагмент…» содержит одну существенную недосказанность: как процесс обнаружения повторяющегося фрагмента связан с циклом посимвольного просмотра неповторяющихся символов. Это отдельный процесс – цикл, или он является частью предыдущего.
// «Склеивание» повторяющихся символов строки.
// Использование счетчика повторений. «Грязная программа»
Мы здесь одним условием убили двух зайцев. В паре неодинаковых символов первый сохраняется всегда, а если он еще заканчивает цепочку повторяющихся, то выводится счетчик.
Здесь есть еще один «заяц». Вспомните, что любой цикл нужно проверять на первый и последний шаг. Они могут «вписаться» в имеющийся текст, а могут и нет. В нашем случае, когда текущий символ – последний в строке, мы сравниваем его с символом «конец строки», т.е. заведомо будет несовпадение и программа сработает правильно. В других случаях, например, когда строка задана объектом или типом данных, состоящим из массива символов и текущей размерности, придется в явном виде записывать условие – последний символ строки. В классическом Си это выглядит так:
if (i!=strlen(in) && in[i]==in[i+1]) k++; // Символ не последний и за ним такой же
Перейдем теперь к решению задачи. Технологически возможны два варианта обработки строки: переписывание в новую или сжатие текущей. Вариант с п ереписыванием будет проще. Мы сможем сохранить «грязную» программу, добавив в нее процесс переписывания – массив и индекс в нем. И не только. Чтобы записать счетчик в виде числа, необходимо перевести его во внешнюю форму представления, в виде цепочки символов-цифр (см.4.5).
// Использование счетчика повторений. Переписывание строки
void F2(char in[], char out[])<
int k1,j1; // Записать k в виде символов-цифр
for (k1=k; k1!=0;k1=k1/10,j++);
out[j++]=in[i]; // Переписать текущий символ
out[j]=0;> // Добавить «конец строки»
Инвариант цикла
// Отдельный цикл «измерения» повторений. «Грязная программа»
for(k=1;in[i]==in[i+k];k++); // Измерить длину цепочки
i=i+k; // Шаг цикла – длина цепочки
// Отдельный цикл «измерения» повторений. «Сжатие строки»
for(k=1;in[i]==in[i+k];k++); // Измерить длину цепочки
j=i+k; // Запомнить начало «хвоста»
int k1,j1; // Записать k в виде символов-цифр
for (k1=k; k1!=0;k1=k1/10,i++);
in[j1]=k%10+’0′; // Затереть символы цифрами числа
i++; // «Оставить» один символ
j1=i; // i – начало следующего шага
Обратите внимание, мы пилим сук, на котором сидим: сдвигаем содержимое части строки, которую еще будем просматривать. Но «пилить» нужно аккуратно, сохраняя свойство, которое мы установили в «грязной» программе: за один шаг цикла мы просматриваем (и преобразуем) фрагмент. Следовательно, по окончании этого шага индекс i должен устанавливаться сразу после сжатого фрагмента (на символе e).
Инвариант цикла и метод математической индукции
Есть еще одна неожиданная параллель между программированием и математикой. В математических доказательствах иногда используется метод математической индукции ( ММИ). Звучит он примерно так: если утверждение верно при i=0, и если из того, что оно верно при произвольном i, можно вывести, что оно будет верно при i+1, то оно будет верно всегда.
На первый взгляд, метод достаточно очевиден: некоторое свойство сохраняется на всей цепочке (последовательности), если оно выполняется в первой точке и сохраняется при переходе из каждой точки в следующую. Но в самом доказательстве есть элемент диалектики общего и частного. Метод определен для последовательности частных шагов, а доказательство проводится в общем виде для произвольного перехода от i-го шага к i+1.
Инвариант цикла может быть разным. Самым простым является утверждение типа: «в начале каждого шага цикл находится в…». Например, программа обработки слов в строке может быть построена по принципу «один шаг = одно слово». Тогда инвариантным утверждением будет: «в начале шага программа находится на начале очередного слова».
// Пословная обработка: «1 шаг = 1 слово». «Грязная программа»
while (in[i]==’ ‘)i++; // ДЛЯ ПЕРВОГО ШАГА
В соответствии с ММИ необходимо обеспечить справедливость утверждения (инварианта) на первом шаге. Для контекста суммирования это естественно: сумма последовательности из 0 элементов равна 0. Для контекста поиска максимума максимальное значение последовательности из 0 элементов или не определено, или не должно быть «меньше меньшего». Поэтому следует в качестве максимума выбирать значение первого элемента, либо использовать «защелку» для первого шага.
for (s=A[0],i=1;i if (A[i]>s) s=A[i];
for (k=-1,i=0; i // поиск минимального из положительных
if (A[i] // пропуск отрицательных
if (k==-1) k=i; // «защелка» на первый положительный
Метод математической индукции как способ доказательства, все же имеет ограниченную область применения. Гораздо важнее, что он является заключительным шагом индуктивного подхода в таких областях формально-логической деятельности как установление зависимостей, вывод формул и т.п.. Сущность его состоит в следующем:
· для решения задачи в общем виде (например, вывода формулы последовательности) первоначально рассматривается одна или несколько конкретных (частых) последовательностей шагов;
· на этой последовательности формально-логически или интуитивно формулируется искомая зависимость;
· справедливость установленной зависимости доказывается (или, наоборот, опровергается) с использованием ММИ.
Снова проведем аналогию с программированием:
· как правило, проектирование цикла начинается с анализа частного случая его работы на конкретной последовательности данных;
· на конкретном примере определяются составные части цикла и из них составляется фрагмент циклической программы;
· определяется инвариант цикла;
· проверяется, во всех ли случаях сохраняется инвариант при переходе от текущего шага к следующему, при необходимости в цикл вводятся коррективы.
При проектировании циклов часто встречаются два вида ошибок, которые имеют прямое отношение к индуктивному принципу его построения:
Что такое инвариант цикла?
Я читаю «Введение в алгоритм» от CLRS. В главе 2 авторы упоминают «петлевые инварианты». Что такое инвариант цикла?
Мне нравится это очень простое определение: ( источник )
Я понимаю, что инвариант цикла является систематическим, формальным инструментом для рассуждения о программах. Мы делаем единственное утверждение, которое сосредотачиваемся на доказательстве истинности, и называем это циклическим инвариантом. Это организует нашу логику. В то же время мы можем неформально спорить о правильности какого-либо алгоритма, но использование инварианта цикла заставляет нас очень тщательно мыслить и гарантирует, что наши рассуждения будут герметичными.
Есть одна вещь, которую многие люди не осознают сразу, имея дело с циклами и инвариантами. Они путаются между инвариантом цикла и условным циклом (условием, контролирующим завершение цикла).
Как указывают люди, инвариант цикла должен быть истинным
(хотя это может временно быть ложным во время тела цикла). С другой стороны, условное условие цикла должно быть ложным после завершения цикла, иначе цикл никогда не завершится.
Таким образом, инвариант цикла и условие цикла должны быть разными условиями.
Хорошим примером инварианта сложного цикла является бинарный поиск.
Предыдущие ответы очень хорошо определили инвариант цикла.
Алгоритм сортировки вставкой (как указано в книге):
Инвариант цикла в этом случае: под-массив [от 1 до j-1] всегда сортируется.
Теперь давайте проверим это и докажем, что алгоритм корректен.
инициализация : до первой итерации j = 2. Таким образом, под-массив [1: 1] является массивом для тестирования. Поскольку у него есть только один элемент, он сортируется. Таким образом, инвариант выполняется.
Обслуживание : это можно легко проверить, проверяя инвариант после каждой итерации. В этом случае это выполняется.
Прекращение : это шаг, на котором мы докажем правильность алгоритма.
Когда цикл заканчивается, значение j = n + 1. Снова цикл-инвариант выполняется. Это означает, что под-массив [от 1 до n] должен быть отсортирован.
Это то, что мы хотим сделать с нашим алгоритмом. Таким образом, наш алгоритм правильный.
Помимо всех хороших ответов, я полагаю, замечательный пример Джеффа Эдмондса из книги « Как думать об алгоритмах» может очень хорошо проиллюстрировать эту концепцию:
ПРИМЕР 1.2.1 «Алгоритм Find-Max с двумя пальцами»
1) Спецификации: входной экземпляр состоит из списка L (1..n) элементов. Вывод состоит из индекса i, такого, что L (i) имеет максимальное значение. Если существует несколько записей с одним и тем же значением, возвращается любая из них.
2) Основные шаги: вы выбираете метод двумя пальцами. Ваш правый палец бежит вниз по списку.
3) Мера прогресса: мера прогресса заключается в том, насколько далеко вдоль списка находится ваш правый палец.
4) Инвариант петли: петли утверждает, что ваш левый палец указывает на одну из самых больших записей, с которыми когда-либо сталкивался ваш правый палец.
5) Основные шаги: на каждой итерации вы перемещаете правый палец вниз на одну запись в списке. Если ваш правый палец сейчас указывает на вход, который больше, чем вход левого пальца, то переместите левый палец, чтобы он был правым.
6) Сделать прогресс: вы делаете успехи, потому что ваш правый палец перемещается на одну запись.
7) Поддерживать инвариант цикла. Вы знаете, что инвариант цикла поддерживается следующим образом. Для каждого шага новым элементом левого пальца является Макс (старый элемент левого пальца, новый элемент). По инварианту цикла это Max (Max (более короткий список), новый элемент). Математически это Макс (длинный список).
8) Создание инварианта петли: Сначала вы устанавливаете инвариант петли, указав двумя пальцами на первый элемент.
9) Условие выхода: вы закончите, когда ваш правый палец закончит обход списка.
10) Окончание: В конце концов, мы знаем, что проблема решается следующим образом. По условию выхода ваш правый палец встретил все записи. С помощью инварианта цикла ваш левый палец указывает на максимум из них. Верните эту запись.
11) Завершение и время выполнения: требуемое время в несколько раз превышает длину списка.
12) Особые случаи: проверьте, что происходит, когда существует несколько записей с одинаковым значением или когда n = 0 или n = 1.
14) Формальное доказательство. Корректность алгоритма следует из приведенных выше шагов.
Следует отметить, что инвариант цикла может помочь в разработке итерационных алгоритмов, если рассматривать утверждение, которое выражает важные отношения между переменными, которые должны быть истинными в начале каждой итерации и когда цикл завершается. Если это имеет место, вычисления находятся на пути к эффективности. Если false, алгоритм потерпел неудачу.
Инвариант в этом случае означает условие, которое должно быть истинным в определенной точке каждой итерации цикла.
Значение инварианта никогда не меняется
Здесь инвариант цикла означает, что «изменение, которое происходит с переменной в цикле (увеличение или уменьшение), не изменяет условие цикла, т.е. условие удовлетворяет», так что концепция инварианта цикла пришла
Это важно для циклического инвариантного доказательства, где можно показать, что алгоритм выполняется правильно, если на каждом этапе его выполнения выполняется свойство инвариантного цикла.
Чтобы алгоритм был корректным, инвариант цикла должен содержать:
Инициализация (начало)
Техническое обслуживание (каждый шаг после)
Прекращение (когда это закончено)
Таким образом, свойство инварианта цикла состоит в том, что выбранный путь имеет наименьший вес. В начале мы не добавляли ребер, поэтому это свойство имеет значение true (в данном случае это не false). На каждом шаге мы следуем по краю наименьшего веса (жадный шаг), поэтому мы снова выбираем путь с наименьшим весом. В конце мы нашли путь с наименьшим весом, поэтому наше свойство также верно.
Если алгоритм этого не делает, мы можем доказать, что он не оптимален.
Работа не переносится на следующий этап сложными, зависящими от данных способами. Каждый проход по циклу не зависит от всех остальных, а инвариант служит для связывания проходов в рабочее целое. Рассуждение о том, что ваш цикл работает, сводится к рассуждению о том, что инвариант цикла восстанавливается при каждом прохождении цикла. Это разбивает сложное общее поведение цикла на маленькие простые шаги, каждый из которых может рассматриваться отдельно. Условие проверки цикла не является частью инварианта. Это то, что заставляет цикл завершаться. Вы рассматриваете отдельно две вещи: почему цикл должен когда-либо завершаться, и почему цикл достигает своей цели, когда завершается. Цикл завершится, если каждый раз, проходя через цикл, вы приближаетесь к выполнению условия завершения. Это часто легко гарантировать: например, пошаговое изменение переменной счетчика до тех пор, пока она не достигнет фиксированного верхнего предела. Иногда обоснование прекращения является более сложным.
Инвариант цикла должен быть создан таким образом, чтобы при достижении условия завершения и инварианта «истина» цель достигалась:
invariant + termination => target
Требуется практика для создания простых и взаимосвязанных инвариантов, которые охватывают все достижения цели, кроме завершения. Лучше всего использовать математические символы для выражения инвариантов цикла, но когда это приводит к слишком сложным ситуациям, мы полагаемся на ясную прозу и здравый смысл.
С точки зрения методологии программирования, инвариант цикла можно рассматривать как более абстрактную спецификацию цикла, которая характеризует более глубокую цель цикла за пределами деталей этой реализации. Обзорная статья охватывает фундаментальные алгоритмы из многих областей информатики (поиск, сортировка, оптимизация, арифметика и т. Д.), Характеризуя каждый из них с точки зрения его инварианта.
СОДЕРЖАНИЕ
Неформальный пример
Логика Флойда – Хора
< C ∧ я >б о d у < я > < я >ш час я л е ( C ) б о d у < ¬ C ∧ я > <\ displaystyle <\ frac <\ 
Пример
В следующем примере показано, как работает это правило. Рассмотрим программу
Тогда можно доказать следующую тройку Хоара:
< Икс ≤ 10 >ш час я л е ( Икс 10 ) Икс знак равно Икс + 1 < Икс знак равно 10 > <\ displaystyle \
< Икс 10 ∧ Икс ≤ 10 >Икс знак равно Икс + 1 < Икс ≤ 10 > <\ Displaystyle \ <х
Исходя из этой предпосылки, правило while петель позволяет сделать следующий вывод:
< Икс ≤ 10 >ш час я л е ( Икс 10 ) Икс знак равно Икс + 1 < ¬ ( Икс 10 ) ∧ Икс ≤ 10 > <\ Displaystyle \ <х \ Leq 10 \>\; <\ mathtt
Поддержка языков программирования
Эйфелева
Язык программирования Whiley также обеспечивает первоклассную поддержку инвариантов цикла. Инварианты цикла выражаются с помощью одного или нескольких where предложений, как показано ниже:
Использование инвариантов цикла
Инвариант цикла может служить одной из следующих целей:
Для 1. достаточно комментария на естественном языке (как // m equals the maximum value in a[0. i-1] в приведенном выше примере).
Для 3. существуют некоторые инструменты для поддержки математических доказательств, обычно основанные на показанном выше правиле Флойда – Хоара, что данный код цикла фактически удовлетворяет заданному (набору) инварианту (ам) цикла.
Технику абстрактной интерпретации можно использовать для автоматического определения инварианта цикла данного кода. Однако этот подход ограничен очень простыми инвариантами (такими как 0 ).
Отличие от кода, инвариантного к циклам
где вычисления x = y+z и x*x можно переместить перед циклом, в результате получится эквивалентная, но более быстрая программа:
Напротив, например, свойство 0 является инвариантом цикла как для исходной, так и для оптимизированной программы, но не является частью кода, поэтому не имеет смысла говорить о «перемещении его из цикла».
Урок 35
Доказательство правильности программ
(§37. Доказательство правильности программ)
Содержание урока
Инвариант цикла
Инвариант цикла
Таким образом, для алгоритма Евклида существует условие НОД(а, b) = НОД(m, n), которое остаётся справедливым на протяжении всего выполнения алгоритма: перед началом цикла, после каждого шага цикла и после окончания работы цикла. Такое условие называется инвариантом цикла (англ. invariant — неизменный).
Инвариант цикла — это соотношение между значениями переменных, которое остаётся справедливым после завершения любого шага цикла.
Выделив в явном виде инвариант каждого цикла, мы избегаем многих возможных ошибок на начальной стадии и делаем первый шаг к доказательству правильности всей программы. Как писал академик Андрей Петрович Ершов, один из первых теоретиков программирования в СССР, «программиста бьют по рукам, если он посмеет написать оператор цикла, не найдя перед этим его инварианта».
Рассмотрим несколько примеров.
Пример 1. Двое играют в следующую игру: перед ними лежат в ряд N + 1 камней, сначала N белых, и в конце цепочки — один чёрный. За один ход каждый может взять от 1 до 3 камней. Проигрывает тот, кто берет чёрный («несчастливый») камень.
Таким образом, для своего выигрыша игрок должен каждым своим ходом восстанавливать инвариант: число оставшихся белых камней должно быть кратно 4. Если инвариант выполнен в начальной позиции, положение проигрышное и первый игрок может надеяться только на ошибку соперника.
Пример 2. Пусть задан массив А длины n. Найдём инвариант цикла в программе суммирования элементов массива:
нц для i от 1 до n
Здесь на каждом шаге к переменной Sum добавляется элемент массива A[i], так что при любом i после окончания очередного шага цикла в Sum накоплена сумма всех элементов массива с номерами от 1 до i. Это и есть инвариант цикла. Поэтому сразу можно сделать вывод о том, что после завершения цикла в переменной Sum будет записана сумма всех элементов массива.
Аналогично можно показать, что в алгоритме поиска наименьшего значения в массиве:
нц для i от 2 до n
если А[i] Пример 3. Для того же массива найдем инвариант цикла в программе сортировки элементов массива методом пузырька:
нц для i от 1 до n-1
если A[j] > A[j+l] то
с:= А[j); А(j]:= А[j+1]; A[j + 1]:= с;
До начала алгоритма элементы расположены произвольно. На каждом шаге внешнего цикла на свое место «всплывает» один элемент массива. Поэтому инвариант этого цикла можно сформулировать так: «После выполнения i-ro шага цикла первые i элементов массива отсортированы и установлены на свои места».
Теперь построим инвариант внутреннего цикла. В этом цикле очередной «лёгкий» элемент поднимается вверх к началу массива. Перед первым шагом внутреннего цикла элемент, который будет стоять на i-м месте в отсортированном массиве, может находиться в любой ячейке от А[i] до А[n]. После каждого шага его «зона нахождения» сужается на одну позицию, так что инвариант внутреннего цикла можно сформулировать так: «Элемент, который будет стоять на i-м месте в отсортированном массиве, может находиться в любой ячейке от A[i] до А[j]». Очевидно, что когда в конце этого цикла j = i, элемент A[i] встаёт на своё место.
В предыдущих примерах мы определяли инвариант готового цикла. Теперь покажем, как можно строить цикл с помощью заранее выбранного инварианта.
Пример 4. Рассмотрим алгоритм быстрого возведения в степень, основанный на использовании операций возведения в квадрат и умножения. Он использует две очевидные формулы:
(1) a k = a k-l • а при нечётной степени k и
(2) а к = (а 2 ) k/2 при чётной степени k.
Покажем, как работает алгоритм, на примере возведения числа а в степень 7:
Здесь поочерёдно применяются первая и вторая формулы. Заметим, что на каждом этапе выражение а n можно представить в виде а n = b к • р, где через р обозначена часть, взятая выше в квадратные скобки. Если нам каким-то образом удастся уменьшить k до нуля, сохранив это равенство, то мы получим а n = р, т. е. задача будет решена, а результат будет находиться в переменной р.
Таким образом, равенство а n = b к • р можно использовать как инвариант цикла. Для того чтобы обеспечить выполнение этого равенства в начальный момент, можно принять, например, b = а, k = n и р = 1. Далее в цикле применяются формулы (1) и (2) (в зависимости от чётности k на данном шаге). Цикл заканчивается, когда k = 0. В результате получаем следующее решение:
нц пока к <> 0
если mod(k,2)=0 то
иначе
Заметим, что инвариант цикла а n = b к • р выполняется до начала цикла, после каждого шага, а также после завершения цикла. Таким образом, мы написали код программы и одновременно доказали правильность этого блока.
Следующая страница 
Спецификация
Cкачать материалы урока