для чего нужен ряд тейлора

Ряд Тейлора. Ряды Маклорена.

Ряд Тейлора — разложение функции в бесконечную сумму степенных функций.

Ряд Тейлора применяют для апроксимации функции многочленами. То есть, линеаризация уравнений проходит путем разложения в ряд Тейлора и отсечения каждого члена старше 1-го порядка.

Определение ряда Тейлора.

Функция f(x) бесконечно дифференцируется в некоторой окрестности т.a:

Этот ряд называется рядом Тейлора функции f в т.a.

Свойства ряда Тейлора.

Если f есть аналитическая функция во всякой точке a, то ряд Тейлора этой функции во всякой точке a области определения f сходится к f в некоторой окрестности a.

Есть бесконечно дифференцируемые функции, ряд Тейлора которых сходится, однако, при этом отличается от функции во всякой окрестности a. Вариант, предложенный Коши:

У этой функции каждые производные в 0 равны нулю, поэтому коэффициенты ряда Тейлора в точке a=0 равны 0.

Если у функция f(x) есть непрерывные производные вплоть до (n+1)-го порядка, то эту функцию можно разложить в степенной ряд по формуле Тейлора:

где R_n − остаточный член в форме Лагранжа определяют так:

Если это разложение сходится в некотором интервале x, т.е. , значит, оно является рядом Тейлора, который представляет разложение функции f (x) в т.a.

Если a = 0, значит, это разложение является рядом Маклорена:

Ряды Маклорена некоторых функций.

1. Экспонента: ,

Источник

Понимание реальности и ряды Тейлора

А в реальном мире нам приходится сталкиваться с множеством весьма прагматичных задач. Например, нам нужно посчитать ту же экспоненту или синус для различных значений аргумента x. Для чего? Экспонента очень хорошо описывает рост популяции микроорганизмов в насыщенной кормом среде, синус и косинус дают прекрасное описание волновых процессов. А все это очень пригодится, когда мы будем строить космические корабли и изобретать вакцины. Конечно, сейчас посчитать экспонету и прочие функции может любой инженерный калькулятор. Но нас, в данном случае, больше интересует сам алгоритм подсчёта, а не его результат.

Ладно, хватит уже пережёвывать прописные истины. Людям, хотя бы поверхностно знакомым с численными методами, всё и так предельно ясно. А остальные разберутся сами, если им будет интересно. К чему я всё это начал? А вот к чему.

Вопрос: можно ли создать Единую Теорию Всего? Да, но чтобы её записать, потребуется бесконечное количество бумаги. Ведь ряд Тейлора бесконечен. Поэтому мы можем лишь бесконечно приближать свои знания к Истине.

И тем не менее мы питаем огромное колличество иллюзий относительно наших представлений о реальном мире. Религии проповедуют, что именно они знают Абсолютную Истину. Многие учёные тоже грешат, цепляясь за старые парадигмы. Мы постоянно ошибаемся, когда выносим наши теории за рамки их допустимой окрестности, либо игнорируем допустимую степень точности в наших «расчётах». Но хуже всего, когда мы принимаем представления, которые явно противоречат реальности, либо никак не соприкасаются с ней.

Источник

Ряд Тейлора. Ряды Маклорена.

Ряд Тейлора — разложение функции в бесконечную сумму степенных функций.

Ряд Тейлора применяют для апроксимации функции многочленами. То есть, линеаризация уравнений проходит путем разложения в ряд Тейлора и отсечения каждого члена старше 1-го порядка.

Определение ряда Тейлора.

Функция f(x) бесконечно дифференцируется в некоторой окрестности т.a:

Этот ряд называется рядом Тейлора функции f в т.a.

Свойства ряда Тейлора.

Если f есть аналитическая функция во всякой точке a, то ряд Тейлора этой функции во всякой точке a области определения f сходится к f в некоторой окрестности a.

Есть бесконечно дифференцируемые функции, ряд Тейлора которых сходится, однако, при этом отличается от функции во всякой окрестности a. Вариант, предложенный Коши:

У этой функции каждые производные в 0 равны нулю, поэтому коэффициенты ряда Тейлора в точке a=0 равны 0.

Если у функция f(x) есть непрерывные производные вплоть до (n+1)-го порядка, то эту функцию можно разложить в степенной ряд по формуле Тейлора:

где R_n − остаточный член в форме Лагранжа определяют так:

Если это разложение сходится в некотором интервале x, т.е. , значит, оно является рядом Тейлора, который представляет разложение функции f (x) в т.a.

Если a = 0, значит, это разложение является рядом Маклорена:

Ряды Маклорена некоторых функций.

1. Экспонента: ,

2. Натуральный логарифм:

3. Биномиальное разложение: для всех |x| <1и всех комплексных α, где:

,

для всех |x|<1,

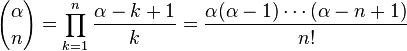
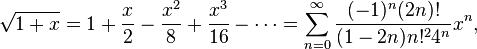
5. Гиперболические функции:

Источник

Ряд Тейлора

Понятие ряда Тейлора.

Если функция \(f(x)\) определена в некоторой окрестности точки \(x_<0>\) и имеет в точке \(x_<0>\) производные всех порядков, то степенной ряд
$$
f(x_<0>) + \sum_^<\infty>\frac(x_<0>)>(x-x_<0>)^\label
$$
называется рядом Тейлора функции \(f\) в точке \(x_<0>\).

Пусть функция \(f\) регулярна в точке \(x_<0>\), то есть представляется в некоторой окрестности точки \(x_<0>\) сходящимся к этой функции степенным рядом
$$
f(x) = \sum_^<\infty>a_(x-x_<0>)^,\quad |x-x_<0>| 0.\label
$$
Тогда по теореме, доказанной здесь, функция \(f\) бесконечно дифференцируема в окрестности точки \(x_<0>\), причем коэффициенты ряда \eqref выражаются формулами
$$
a_ <0>= f(x_<0>),\quad a_ = \frac(x_<0>)>,\quad n \in \mathbb.\label
$$
Таким образом, степенной ряд для функции \(f(x)\), регулярной в данной точке \(a\), совпадает с рядом Тейлора функции \(f\) в точке \(a\).

Если известно, что функция \(f(x)\) бесконечно дифференцируема в точке \(a\) (и даже в некоторой окрестности этой точки), то нельзя утверждать, что составленный для этой функции ряд Тейлора \eqref сходится при \(x \neq x_<0>\) к функции \(f(x)\).

Рассмотрим функцию \(f(x) = e^<-1/x^<2>>\), \(x \neq 0\), \(f(0) = 0\). Эта функция определена на \(R\),
$$
f'(x) = \frac<2>>e^<-1/x^<2>>,\ f″(x) = \left(\frac<4>>-\frac<6>>\right)e^<-1/x^<2>>\quad\mbox<при>\ x \neq 0,\nonumber
$$
откуда с помощью индукции легко показать, что
$$
f^<(n)>(x) = e^<-1/x^<2>> Q_ <3n>\left(\frac<1>\right)\ \mbox<при>\ x \neq 0,\nonumber
$$
где \(Q_<3n>(t)\) — многочлен степени \(3n\) от \(t\). Воспользуемся тем, что \(\displaystyle\lim_\frac<1><|x|^>e^<-1/x^<2>>=0\) для любого \(k \in \mathbb\) (решение можно посмотреть здесь), и докажем, что
$$
f^<(k)>(0) = 0\ \mbox<для любого>\ k \in \mathbb.\label
$$
Утверждение \eqref верно при \(k = 1\), так как \(f'(0) = \displaystyle\lim_\frac>> = 0\), откуда, предположив, что формула \eqref справедлива при \(k = n\), находим
$$
f^<(n + 1)>(0) = \lim_\frac(x)-f^<(n)>(0)> = \lim_ \frac<1> Q_ <3n>\left(\frac<1>\right) e^<-1/x^<2>> = 0.\nonumber
$$
Таким образом, по индукции доказано равенство \eqref, и поэтому все коэффициенты ряда Тейлора \eqref в точке \(x_ <0>= 0\) для рассматриваемой функции равны нулю.

Так как \(e^<-1/x^<2>> \neq 0\) при \(x \neq 0\), то сумма ряда Тейлора для функции \(f\) не совпадает с \(f(x)\) при \(x \neq 0\). Иначе говоря, эту функцию нельзя представить рядом Тейлора, сходящимся к ней в окрестности точки \(x_ <0>= 0\).

Причина этого явления становится понятной, если функцию \(f\) рассматривать в комплексной плоскости. В самом деле, функция \(f(z) = e^<-1/z^<2>>\) не является непрерывной в точке \(z = 0\), так как \(f(x) = e^<-1/x^<2>> \rightarrow 0\) при \(x \rightarrow 0\), a \(f(iy) = e^<1>> \rightarrow +\infty\) при \(y \rightarrow 0\).

Остаточный член формулы Тейлора.

Пусть функция \(f(x)\) бесконечно дифференцируема в точке \(x_<0>\). Тогда ей можно поставить в соответствие ряд \eqref. Обозначим
$$
S_(x) = \sum_^\frac(x_<0>)>(x-x_<0>)^,\label
$$
$$
r_(x) = f(x)-S_(x)\label
$$
и назовем \(r_(x)\) остаточным членом формулы Тейлора для функции \(f\) в точке \(x_<0>\). Если существует
$$
\lim_ r_(x) = 0,\label
$$
то согласно определению сходимости ряда ряд \eqref сходится к функции \(f(x)\) в точке \(x\), то есть
$$
f(x) = \sum_^<\infty>\frac(x_<0>)>(x-x_<0>)^.\label
$$

Если функции \(f(x)\), \(f'(x)\), …, \(f^<(n + 1)>(x)\) непрерывны на интервале \(\Delta = (x_<0>-\delta, x_ <0>+ \delta)\), где \(\delta > 0\), то для любого \(x \in \Delta\) остаточный член формулы Тейлора для функции \(f\) в точке \(x_<0>\) можно представить:

\(\circ\) Формула \eqref доказана в здесь. Докажем формулу \eqref методом индукции. В силу равенств \eqref и \eqref нужно показать, что
$$
f(x)-f(x_<0>) = \sum_^\frac(x_<0>)>(x-x_<0>)^ + \frac<1> \int\limits_>^ (x-t)^f^<(n + 1)>(t)\ dt.\label
$$

Если функция \(f\) и все ее производные ограничены в совокупности на интервале \(\Delta = (x_<0>-\delta, x_ <0>+ \delta)\), то есть
$$
\exists M > 0: \forall x \in \Delta \rightarrow |f^<(n)>(x)| \leq M,\ n = 0,1,2,\ldots,\label
$$
то функция \(f\) представляется сходящимся к ней в каждой точке интервала \(\Delta\) рядом Тейлора \eqref.

\(\circ\) Пусть \(x \in (x_<0>-\delta, x_ <0>+ \delta)\). Тогда, используя формулу \eqref и условие \eqref, получаем
$$
|r_(x)| \leq M \frac<|x-x_<0>|^><(n + 1)!>.\label
$$

Так как \(\displaystyle\lim_ \frac> = 0\) для любого \(a > 0\) (пример разобран здесь), то из \eqref следует, что выполняется условие \eqref, то есть в точке \(x\) справедливо равенство \eqref. \(\bullet\)

Теорема 2 остается в силе, если условие \eqref заменить следующим условием:
$$
\exists M > 0\ \exists C > 0: \forall x \in \Delta \rightarrow |f^<(n)>(x)| \leq MC^,\ n = 0, 1, 2, \ldots\nonumber
$$

Разложение элементарных функций в ряд Тейлора.

Найдем разложение основных элементарных функций в ряд Тейлора в окрестности точки \(x_ <0>= 0\), то есть в ряд вида
$$
f(x) = \sum_^<\infty>\frac(0)>x^,\label
$$
который называют рядом Маклорена. Заметим, что коэффициенты \(\displaystyle\frac(0)>\) разложения \eqref для основных элементарных функций (показательной, гиперболических, тригонометрических и других) были найдены в разделе про формулу Тейлора.

Разложение показательной и гиперболической функций в ряд Тейлора.

Пусть \(f(x) = e^\). Тогда для любого \(x \in (-\rho, \rho)\), где \(\rho > 0\), выполняются неравенства
$$
0 0\), то есть радиус сходимости этого ряда \(R = +\infty\). Так как для функции \(f(x) = e^\) выполняются равенства \(f(0) = 1\), \(f^<(n)>(0) = 1\) для любого \(n\), то по формуле \eqref получаем разложение в ряд Маклорена показательной функции
$$
e^ = \sum_^<\infty>\frac>,\label
$$

Используя разложение \eqref и формулы
$$
\operatorname x = \frac + e^<-x>><2>,\quad \operatorname x = \frac-e^<-x>><2>,\nonumber
$$
находим разложения в ряд Маклорена гиперболического косинуса и гиперболического синуса:
$$
\operatorname x = \sum_^<\infty>\frac><2n!>,\label
$$
$$
\operatorname x = \sum_^<\infty>\frac><(2n + 1)!>,\label
$$
Радиус сходимости каждого из рядов \eqref, \eqref \(R = +\infty\).

Разложение тригонометрических функций в ряд Тейлора.

Пусть \(f(x) = \sin x\). Тогда \(|f(x)| \leq 1\) и \(|f^<(n)>(x)| \leq 1\) для всех \(n \in \mathbb\) и для всех \(x \in R\). По теореме 2 ряд \eqrefдля функции \(f(x) = \sin x\) сходится для любого \(x \in (-\infty, +\infty)\), то есть радиус сходимости этого ряда \(R = +\infty\).

Если \(f(x) = \sin x\), то \(f(0) = 0\), \(f^<(2n)>(0) = 0\), \(f'(0) = 1\), \(f^<(2n + 1)>(0) = (-1)^\) для любого \(n\), и по формуле\eqrefполучаем разложение синуса в ряд Маклорена:
$$
\sin x = \sum_<\substack>^ <\infty>\frac<(-1)^><(2n + 1)!>x^<2n + 1>.\label
$$

Пусть \(f(x) = \cos x\). Тогда \(|f(x)| \leq 1\), \(|f^<(n)>(x)| \leq 1\) для всех \(n\) и для всех \(x \in R\), \(f(0) = 1\), \(f'(0) = 0\), \(f^<(2n)>(0) = (-1)^\) и, \(f^<(2n + 1)>(0) = 0\) для всех \(n\). По формуле \eqref получаем
$$
\cos x = \sum_^ <\infty>\frac<(-1)^><2n!>x^<2n>.\label
$$
Радиус сходимости каждого из рядов \eqref и \eqref \(R = +\infty\).

Разложение логарифмической функции в ряд Тейлора.

\(\circ\) Оценим остаточный член \(r_(x)\), пользуясь формулой \eqref при \(x_ <0>= 0\). Преобразуем эту формулу, полагая \(t = \tau x\). Тогда \(dt = x\ d\tau\), \(1-x =x(1-\tau)\) и формула \eqref примет вид
$$
r_(x) = \frac> \int\limits_0^1 (1-\tau) f^<(n + 1)>(\tau x) d\tau.\label
$$

Если \(f(x) = \ln(x + 1)\), то по формуле \eqref, используя равенство \eqref, получаем
$$
r_(x) = (-1)^x^ \int\limits_0^1 \frac<(1-\tau)^><(1 + \tau x)^> d \tau.\label
$$

Пусть \(|x| 1\), то \(\displaystyle\lim_ \frac><(1/|x|)^> = 0\). Поэтому из соотношения \eqref следует, что \(r_(x) \rightarrow 0\) при \(n \rightarrow \infty\) для каждого \(x \in (-1, 1)\), то есть справедливо равенство \eqref, причем радиус сходимости ряда \eqref в случае, когда \(\alpha \neq 0\) и \(\alpha \notin \mathbb\), равен 1. \(\bullet\)

В заключение заметим, что при разложении функций в ряд Тейлора обычно используют формулы \eqref—\eqref, \eqref-\eqref и применяют такие приемы, как: представление данной функции в виде линейной комбинации функций, ряды Тейлора для которых известны; замена переменного; почленное дифференцирование и интегрирование ряда.

Разложить в ряд Маклорена функцию \(f(x)\) и найти радиус сходимости \(R\) ряда, если:

Разложить в ряд Маклорена функции
$$
\operatorname x,\nonumber
$$
$$
\operatorname x,\nonumber
$$
$$
\ln(x + \sqrt<1 + x^<2>>),\nonumber
$$
и найти радиусы сходимости \(R\) рядов.

Разложить в ряд Тейлора в точке \(x_ <0>= 2\) функцию \(f(x) = \ln(4 + 3x-x^<2>)\).

Элементарные функции комплексного переменного.

Используя равенства \eqref и формулы \eqref, \eqref, находим
$$
\frac + e^<-iz>> <2>= \cos z,\ \frac-e^<-iz>> <2i>= \sin z,\label
$$
откуда следует, что
$$
e^ = \cos z + i \sin z.\label
$$
Полагая в формуле \eqref \(z = z_<1>\) и \(z = z_<2>\). и перемножая соответствующие ряды, можно показать, что
$$
e^>e^> = e^ + z_<2>>.\label
$$

Пусть \(z = x + iy\), где \(x \in R\), \(y \in R\). Тогда из равенства \eqref и формулы \eqref находим
$$
e^ = e^ = e^(\cos y + i \sin y).\label
$$
Из формулы \eqref следует, что
$$
e^ = e^,\nonumber
$$
то есть \(e^\) — периодическая функция с периодом \(2\pi i\). Поэтому для каждого комплексного \(z \neq 0\) уравнение
$$
e^ = z\label
$$
имеет бесконечное множество решений вида \(w + i2\pi n\), где \(w\) — одно из решений уравнения \eqref, \(n \in Z\).

Если \(w = u + iv\), то \(z = e^ = e^(\cos v + i \sin v)\), откуда получаем
$$
|z| = e^,\quad u = \ln |z|,\quad v = \arg z.\nonumber
$$

Пусть \(\varphi\) — какое-нибудь значение аргумента числа \(z\). Тогда
$$
v = \varphi + 2\pi n,\ n \in Z.\nonumber
$$
Таким образом, все решения уравнения \eqref, если их обозначить символом \(\operatorname\ z\), задаются формулой
$$
\operatorname\ z = \ln |z| + i(\varphi + 2\pi n),\label
$$
где \(\varphi\) — одно из значений аргумента числа \(z\) \((z \neq 0)\), \(n \in Z\).

По заданному значению \(z\) значение \(w\) из уравнения \eqref определяется, согласно формуле \eqref, неоднозначно (говорят, что логарифмическая функция \(\operatorname\ z\) является многозначной).

Разложить в степенной ряд в окрестности точки \(z = 0\) функцию \(f(z) = e^\sin z\).

\(\triangle\) Используя формулы \eqref и \eqref, получаем
$$
f(z) = e^\left(\frac-e^<-iz>><2i>\right) = \frac<1><2i>(e^-e^).\nonumber
$$
Так как \(1 + i = \sqrt<2>e^\), \(1-i = \sqrt<2>e^<-i\pi/4>\), то по формуле \eqref находим
$$
f(z) = \sum_^ <\infty>\frac<2^> \left(\frac-e^<-i\pi n/4>><2i>\right)z^,\nonumber
$$
откуда в силу второго из равенств \eqref следует, что
$$
e^\sin z = \sum_^ <\infty>\frac<2^> \sin \frac<\pi n><4>z^.\nonumber
$$
Радиус сходимости ряда \(R = +\infty\). \(\blacktriangle\)

Источник

СОДЕРЖАНИЕ

Определение

Примеры

так что серия Тейлора для 1 / Икс при = 1 является

Соответствующий ряд Тейлора для ln x при a = 1 имеет вид

и, в более общем смысле, соответствующий ряд Тейлора для ln x в произвольной ненулевой точке a равен:

История

Аналитические функции

Если f ( x ) задается сходящимся степенным рядом в открытом диске (или интервале в вещественной прямой) с центром в точке b на комплексной плоскости, она называется аналитической в этом круге. Таким образом, для x в этом круге f задается сходящимся степенным рядом

Дифференцируя приведенную выше формулу по x n раз, тогда установка x = b дает:

и поэтому разложение в степенной ряд согласуется с рядом Тейлора. Таким образом, функция является аналитической в ​​открытом диске с центром в точке b тогда и только тогда, когда ее ряд Тейлора сходится к значению функции в каждой точке диска.

Использование ряда Тейлора для аналитических функций включает:

Ошибка аппроксимации и сходимость

Обобщение

В общем, для любой бесконечной последовательности a _i выполняется следующее тождество степенного ряда:

Список некоторых общих функций серии Маклорена

Экспоненциальная функция

Экспоненциальная функция (с базой е ) имеет ряд Маклорена е Икс <\ displaystyle e ^ >

Натуральный логарифм

Натуральный логарифм (с основанием е ) имеет ряд Маклорена

Геометрическая серия

В геометрической прогрессии и его производные имеют ряд Маклорена

Биномиальный ряд

Биномиальный ряд является степенным рядом

коэффициенты которого являются обобщенными биномиальными коэффициентами

Тригонометрические функции

Обычные тригонометрические функции и их обратные имеют следующий ряд Маклорена:

Гиперболические функции

Расчет ряда Тейлора

Первый пример

Чтобы вычислить полином Маклорена 7-й степени для функции

сначала можно переписать функцию как

Ряд Тейлора для натурального логарифма равен (с использованием нотации большой O )

а для косинусной функции

Второй пример

Предположим, нам нужен ряд Тейлора в 0 функции

Для экспоненциальной функции

и, как в первом примере,

Предположим, что степенной ряд равен

е Икс потому что ⁡ Икс знак равно c 0 + c 1 Икс + c 2 Икс 2 + c 3 Икс 3 + ⋯ <\ displaystyle <\ frac > <\ cos x>> = c_ <0>+ c_ <1>x + c_ <2>x ^ <2>+ c_ <3>x ^ <3>+ \ cdots \!>

Тогда умножение на знаменатель и подстановка ряда косинуса дает

Сбор сроков до четвертого порядка доходности

Третий пример

Ряд Тейлора как определения

Ряд Тейлора от нескольких переменных

Ряд Тейлора также может быть обобщен на функции более чем одной переменной с

Разложение в ряд Тейлора второго порядка скалярнозначной функции более чем одной переменной можно компактно записать как

который следует понимать как еще более сокращенную многоиндексную версию первого уравнения этого параграфа с полной аналогией со случаем одной переменной.

Пример

сначала вычисляются все необходимые частные производные:

Оценка этих производных в начале координат дает коэффициенты Тейлора

Подставляя эти значения в общую формулу

Сравнение с рядом Фурье

Источник