для чего нужна гистограмма статистика

Гистограмма

Гистограмма, это способ представления статистических данных в графическом виде – в виде столбчатой диаграммы. Она отображает распределение отдельных измерений параметров изделия или процесса. Иногда ее называют частотным распределением, так как гистограмма показывает частоту появления измеренных значений параметров объекта.

Высота каждого столбца указывает на частоту появления значений параметров в выбранном диапазоне, а количество столбцов – на число выбранных диапазонов.

Важное преимущество гистограммы заключается в том, что она позволяет наглядно представить тенденции изменения измеряемых параметров качества объекта и зрительно оценить закон их распределения. Кроме того, гистограмма дает возможность быстро определить центр, разброс и форму распределения случайной величины. Строится гистограмма, как правило, для интервального изменения значений измеряемого параметра.

Порядок построения гистограммы следующий:

1. Собираются статистические данные – результаты измерений параметра объекта. Для того, чтобы гистограмма позволяла оценить вид распределения случайной величины предпочтительно иметь не менее тридцати результатов измерений.

2. Выявляется наибольшее и наименьшее значение показателя среди полученных результатов измерений.

3. Определяется ширина диапазона значений показателя – из наибольшего значения показателя вычитается наименьшее значение.

4. Выбирается надлежащее число интервалов в пределах которых необходимо сгруппировать результаты измерений.

5. Устанавливаются границы интервалов. Границы интервалов необходимо установить так, чтобы значения данных не попадали ни на одну из границ интервала. Например, если были выбраны интервалы с границами от 0,5 до 5,5 от 5,5 до 10,5 и т.д. то значение данных 5,5 будет попадать как в первый, так и во второй интервал. Чтобы избежать этой проблемы можно изменить интервалы от 0,51 до 5,50 от 5,51 до 10,50 и так далее, таким образом ни одно значение данных не попадет на границу интервала.

6. Подсчитывается число попаданий значений результатов измерений в каждый из интервалов.

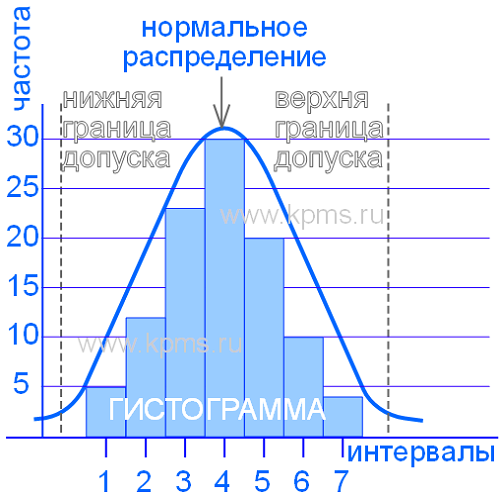
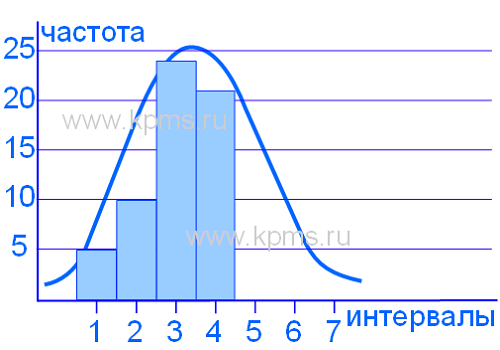
7. Строится гистограмма – на оси абсцисс (горизонтальной оси) отмечаются интервалы, а на оси ординат (вертикальной оси) отмечается частота попаданий результатов измерений в каждый интервал. Интервалы можно устанавливать в натуральных единицах (если позволяет масштаб), т.е. в тех единицах, в которых проводились измерения, либо каждому интервалу можно присвоить порядковый номер и отмечать на оси абсцисс номера интервалов. В результате получается столбчатая диаграмма, представленная на рисунке ниже.

Если на контролируемый параметр существует поле допуска, то гистограмма может содержать верхнюю и нижнюю границы поля допуска. Это позволяет увидеть в какую сторону и как смещается значение контролируемого показателя относительно поля допуска. Границы наносятся по оси абсцисс.

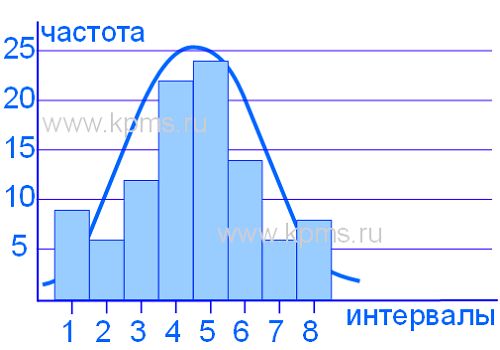
Гистограмма, представленная на рисунке выше имеет форму нормального распределения, что говорит о стабильности процесса, но часто бывает, что форма распределения отклоняется от нормального. Это свидетельствует о нарушениях в процессе и необходимости применения управляющих воздействий.

Некоторые, часто встречающие отклонения и их причины представлены ниже.

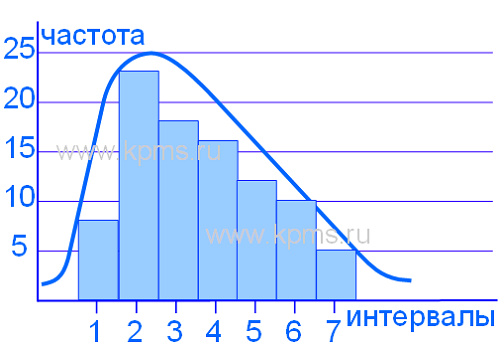
Гистограмма смещена влево (асимметрия влево):

Может вызываться смещением процесса к верхней границе допуска, либо из множества измерений отсортированы результаты, которые выпадают за пределы верхней границы допуска, либо природа процесса физически запрещает любые измерения больше чем максимальные значения допуска.

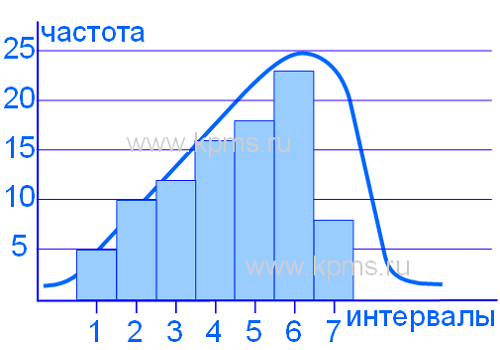
Гистограмма смещена вправо (асимметрия вправо):

Может вызываться смещением процесса к нижней границе допуска, либо из множества измерений отсортированы результаты, которые выпадают за пределы нижней границы допуска, либо природа процесса физически запрещает любые измерения меньше чем минимальные значения допуска.

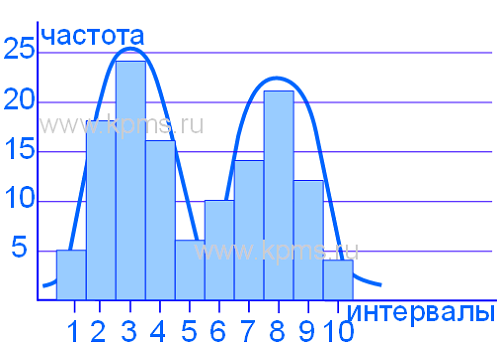
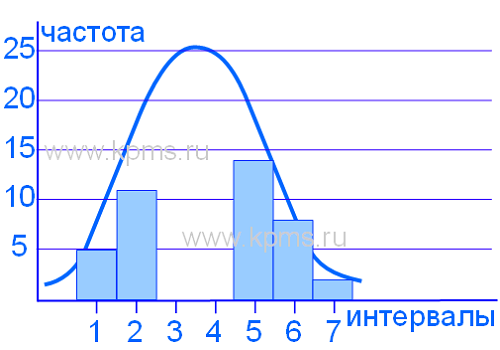
Гистограмма отображает два совмещенных процесса. Такая ситуация может произойти если результаты измерений получены от двух разных устройств, двух операторов, контролеров, разных измерительных инструментов, или с разных точек измерения.

Распределение не является нормальным т.к. нет постепенного снижения частоты результатов измерений от центра к границам допуска. Такой вид гистограммы возникает если процесс не способен удовлетворять спецификациям и часть измерений отсортирована с двух сторон при приближении к границам допуска, либо потеряны чересчур малые значения результатов измерений.

Гистограмма не имеет центра:

Центр распределения был отсортирован из набора данных результатов измерений. Такая ситуация может возникнуть из-за недостаточных требований в инженерной спецификации.

Гистограмма содержит выступы на границах:

Часть измерений на удаленных от центра сторонах распределения была изменена, чтобы привести характеристики процесса в соответствие с установленным полем допуска или измерения, выходящие за пределы поля допуска были записаны как входящие в поле допуска.

Сильные стороны гистограммы, как инструмента контроля качества, заключаются в ее наглядности, простоте, возможности быстро представить вид распределения большого числа данных. Также гистограмма показывает взаимосвязь изменения контролируемых параметров по отношению к инженерным спецификациям.

К недостаткам можно отнести – отсутствие возможности количественно оценить стабильность процесса, отсутствие привязки ко времени, необходимость большого числа данных для точной оценки структуры распределения, возможность различного толкования результатов, некоторая субъективность в представлении формы распределения.

Инструмент «гистограмма» входит в состав сборника «Семь инструментов качества». Сборник можно приобрести в интернет-магазине «Менеджмент качества».

Семь инструментов качества

Семь инструментов качества

Брошюра «Семь инструментов качества» содержит справочную информацию об основных инструментах менеджмента качества. В брошюре представлено описание и даны примеры применения следующих инструментов менеджмента качества:

Источник

6 причин, по которым вам следовало бы отказаться от гистограмм

Гистограммам не чужды систематические ошибки. Дело в том, что они достаточно условны и могут привести к неправильным выводам о данных. Если вы хотите визуализировать переменную, лучше выбрать другой график.

Независимо от того, находитесь ли вы на встрече с высшим руководящим составом или со специалистами по обработке данных, в одном вы можете быть уверены: в какой-то момент появится гистограмма.

И нетрудно догадаться почему. Гистограммы весьма интуитивно наглядны: любой поймет их с первого взгляда. Более того, они объективно представляют реальность, не так ли? А вот и нет.

Гистограмма может ввести в заблуждение и привести к ошибочным выводам — ​​даже на простейшем наборе данных!

В этой статье мы на примерах рассмотрим 6 причин, почему, когда дело доходит до визуализации данных, гистограммы точно не является лучшим выбором:

Они слишком сильно зависят от количества интервалов.

Они слишком сильно зависят от максимума и минимума переменной.

Они не дают возможности заметить значимые значения переменной.

Они не позволяют отличить непрерывные переменные от дискретных.

Они делают сравнение распределений сложным.

Их построение затруднено, если в памяти находятся не все данные.

«Ладно, я понял: гистограммы не идеальны. Но есть ли у меня выбор?» Конечно есть!

В конце статьи я порекомендую другой график, называемый CDP, который минует эти недостатки.

Итак, что же не так с гистограммой?

1. Она слишком сильно зависит от количества интервалов.

Чтобы построить гистограмму, вы должны сначала определить количество интервалов, также называемых корзинами (bins). Для этого существует множество различных практических методов (вы можете ознакомиться с их обзором на этой странице). Но насколько критичен этот выбор? Давайте возьмем реальные данные и посмотрим, как меняется гистограмма в зависимости от количества интервалов.

Переменная представляет собой максимальную частоту сердечных сокращений (ударов в минуту), полученную у 303 людей во время некоторой физической активности (данные взяты из набора данных UCI по сердечным заболеваниям: источник).

Как изменяется гистограмма при изменении количества интервалов. [Рисунок автора]

Глядя на верхний левый график (который мы получим по умолчанию в Python и R), у нас сложится впечатление хорошего распределения с одним пиком (модой). Однако если бы мы рассмотрели бы другие варианты гистограммы, мы получили бы совершенно другую картину. Разные гистограммы одних и тех же данных могут привести к противоречивым выводам.

2. Она слишком сильно зависит от максимума и минимума переменной.

Даже после того, как количество интервалов установлено, интервалы зависят от положения минимума и максимума переменной. Достаточно, чтобы один из них немного изменился, и все интервалы также изменятся. Другими словами, гистограммы не являются надежными.

Например, давайте попробуем изменить максимум переменной, не меняя количество интервалов.

Как меняется гистограмма при изменении максимального значения. [Рисунок автора]

Отличается только одно значение, а весь график получается другим. Это нежелательное свойство, потому что нас интересует общее распределение: одно значение не должно так влиять на график!

3. Не дает возможности заметить значимые значения переменной.

Если в общем, то когда переменная содержит некоторые часто повторяющиеся значения, нам конечно нужно об этом знать. Однако гистограммы этому препятствуют, поскольку они основаны на интервалах, а интервалы «скрывают» отдельные значения.

Классическим примером является случай, когда отсутствующим значениям массово присваивается 0. В качестве примера давайте рассмотрим набор данных переменной, состоящий из 10 тысяч значений, 26% из которых — нули.

Те же данные, разная ширина интервала. На левом графике невозможно обнаружить высокую концентрацию нулей. [Рисунок автора]

График слева — это то, что вы получаете по умолчанию в Python. Глядя на него, вы не заметите скопление нулей, и вы даже можете подумать, что эта переменная имеет «плавную» динамику.

График справа получен путем сужения интервалов и дает более четкое представление о реальности. Но дело в том, что как бы вы ни сужали интервалы, вы никогда не будете уверены, содержит ли первый интервал только 0 или какие-то другие значения.

4. Не позволяет отличить непрерывные переменные от дискретных.

Зачастую мы бы хотели знать, является ли числовая переменная непрерывной или дискретной. По гистограмме это практически невозможно сказать.

Возьмем переменную «Возраст» (Age). Вы можете получить Возраст = 49 лет (когда возраст округлен) или Возраст = 49,828884325804246 лет (когда возраст рассчитывается как количество дней с момента рождения, деленное на 365,25). Первая — дискретная переменная, вторая — непрерывная.

Слева непрерывная переменная. Справа дискретная переменная. Однако на верхних графиках они выглядят одинаково. [Рисунок автора]

Тот, что слева, непрерывен, а тот, что справа, дискретен. Однако на верхних графиках (по умолчанию в Python) вы не увидите никакой разницы между ними: они выглядят совершенно одинаково.

5. Сложно сравнивать распределения.

Часто бывает необходимо сравнить одну и ту же переменную в разных кластерах. Например, в отношении данных UCI о сердечных заболеваниях, приведенных выше, мы можем сравнить:

все население (для справки)

люди моложе 50 страдающие сердечными заболеваниями

люди моложе 50 НЕ страдающие сердечными заболеваниями

люди старше 60 лет страдающие сердечными заболеваниями

люди старше 60 и НЕ страдающие сердечными заболеваниями.

Вот что мы получили бы в итоге:

Сравнение гистограмм. [Рисунок автора]

Гистограммы основаны на областях, и, когда мы пытаемся провести сравнение, области в конечном итоге перекрываются, что делает эту задачу практически невыполнимой.

6. Сложно построить, если в памяти находятся не все данные.

Если все ваши данные находятся в Excel, R или Python, построить гистограмму легко: в Excel вам просто нужно кликнуть по иконке гистограммы, в R — выполнить команду hist(x), а в Python — plt.hist(х).

Но предположим, что ваши данные хранятся в базе данных. Вы же не хотите выгружать все данные только для того, чтобы построить гистограмму, верно? По сути, все, что вам нужно, это таблица, содержащая для каждого интервала крайние значения и количество наблюдений. Примерно такая:

| INTERVAL_LEFT | INTERVAL_RIGHT | COUNT |

| 75.0 | 87.0 | 31 |

| 87.0 | 99.0 | 52 |

| 99.0 | 111.0 | 76 |

Но получить ее с помощью SQL-запроса не так просто, как кажется. Например, в Google Big Query код будет выглядеть так:

Немного громоздко, не правда ли?

Альтернатива: график кумулятивного распределения.

График кумулятивного распределения — это график квантилей переменной. Другими словами, каждая точка CDP показывает:

по оси x: исходное значение переменной (как в гистограмме);

по оси y: сколько наблюдений имеют такое же или меньшее значение.

Давайте посмотрим на пример с переменной — максимальной частотой пульса.

График кумулятивного распределения максимальной частоты сердечных сокращений. [Рисунок автора]

Возьмем точку с координатами x = 140 и y = 90 (30%). По горизонтальной оси вы видите значение переменной: 140 ударов сердца в минуту. По вертикальной оси вы видите количество наблюдений, у которых частота сердцебиение равна или ниже 140 (в данном случае 90 человек, что означает 30% выборки). Следовательно, у 30% нашей выборки максимальная частота сердцебиения составляет 140 или менее ударов в минуту.

Какой смысл в графике, показывающем, сколько наблюдений «равно или ниже» заданного уровня? Почему не просто «равно»? Потому что в противном случае результат зависел бы от отдельных значений переменной. И это не сработает, потому что каждое значение имеет очень мало наблюдений (обычно только одно, если переменная непрерывна). Напротив, CDP полагаются на квантили, которые более стабильны, выразительны и легко читаются.

Вдобавок CDP намного полезнее. Если задуматься, вам часто приходится отвечать на такие вопросы, как «у скольких из них от 140 до 160?» Или «у скольких из них больше 180?». Имея перед глазами CDP, вы можете дать немедленный ответ. С гистограммой это было бы невозможно.

CDP решает все проблемы, которые мы видели выше. Фактически, по сравнению с гистограммой:

1. Не требует пользовательского выбора. Для одного набора данных, существует только один возможный CDP.

2. Не страдает от выпадающих значений. Экстремальные значения не влияют на CDP, поскольку квантили не меняются.

3. Позволяет определять значимые значения. Если существует концентрация точек данных на каком-то конкретном значении, это сразу видно, поскольку будет вертикальный сегмент, соответствующий значению.

4. Позволяет с первого взгляда распознать дискретную переменную. Если существует только конкретный набор возможных значений (т.е. переменная дискретна), это сразу видно, поскольку кривая примет форму лестницы.

5. Упрощает сравнение распределений. На одном графике легко сравнить два или более распределения, поскольку это просто кривые, а не области. Кроме того, ось y всегда находится в диапазоне от 0 до 100%, что делает сравнение еще более простым. Для сравнения, это пример, который мы видели выше:

Сравнение распределений в CDP. [Рисунок автора]

6. Его легко построить, даже если у вас нет всех данных в памяти. Все, что вам нужно, это квантили, которые можно легко получить с помощью SQL:

Как построить график кумулятивного распределения в Excel, R, Python

В R это делается в одну строчку:

Спасибо за внимание! Надеюсь, эта статья оказалась для вас полезной.

Я ценю отзывы и конструктивную критику. Если вы хотите поговорить об этой статье или других связанных темах, вы можете написать мне в Linkedin.

Перевод материала подготовлен в рамках онлайн-курса «Machine Learning. Basic«. Всех заинтересованных приглашаем на день открытых дверей курса, где можно будет узнать все подробности об обучении и пообщаться с преподавателем.

Источник

Гистограмма

Добавлено в закладки: 0

Что такое гистограмма? Описание и определение понятия

Гистограмма – это один из видов диаграмм, представляющий собой графическое изображение определенных статистических показателей и величин в виде столбиков. Основанием для составления диаграммы служит количественный признак. В общем виде, Гистограмма – это ряд смежных прямоугольников, выстраивающихся в ряд на прямой линии. При этом, площадь каждого из них является пропорциональной частоте, данной величине представленной в данной совокупности.

Гистограмм (от др.-греч. черта, буква, написание) — способ графического представления табличных данных.

Гистограмма в статистике

Рассмотрим более детально термин гистограмма

В большинстве статистических расчетов имеем дело либо со случайными данными, которые получены в ходе какого-либо эксперимента (выводящиеся из файла или печатаются непосредственно в документе), либо с результатами генерации случайных чисел, которые рассмотрены в предыдущих разделах встроенными функциями, которые моделируют то или иное явление методом Монте-Карло.

Гистограммой называется график, который аппроксимирует по случайным данным плотность их распределения. При построении гистограммы область значений случайной величины (а,b> разбивают на некоторое количество bin сегментов, а затем подсчитывают процент попадания данных в каждый сегмент.

Гистограмма представляет собой столбчатой график, который построен по полученным за определенный период (к примеру, за неделю или за месяц) данным, разбиваемые на несколько интервалов; число данных, которые попадают в каждый из интервалов (частота), должно выражаться высотой столбика.

Данные для построения гистограммы собирают в течение длительного периода – недели, месяца, года и т. д.

Гистограмма – это серия столбиков одинаковой ширина, но разной высота, которая показывает рассеяние и распределения данных. Ширина столбика – это интервал в диапазоне наблюдений, высотой – количество данных, которая приходится на ту или иную часть интервала, т.е. част ость. По существу, гистограмма может отображать распределение исследуемого показателя. Гистограмме позволено оценить характер рассеивания показателя и разобираться в там, на чём следует сосредотачивать усилия пo улучшению.

Как построить гистограмму?

Чтобы построить гистограмму, нарисуйте горизонтальную и вертикальную оси. Горизонтальная ось (Х) будет отображать интервалы; вертикальная ось (Y), будет отображать частоты. Нарисуйте полоску, которая представляет собой частотность данных в каждом классе. Полоски должны соприкасаться друг с другом.

Использование гистограмм

Гистограмму используют для изображения только интервальных рядов.

К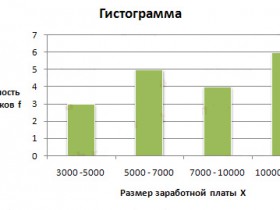оличественные соотношения некоторого показателя представлены в виде прямоугольников, площади которых пропорциональны. Чаще всего для удобства восприятия ширину прямоугольников берут одинаковую, при этом их высота определяет соотношения отображаемого параметра.

В статистике гистограмма — геометрическое изображение эмпирической функции плотности вероятности некоторой случайной величины, которое построено по выборке.

В фотографии гистограммой называют графическое представление распределения яр костей фотоснимка.

Гистограмма – это один из тех немногих способов графического представления данных, доступность и легкость восприятия которого не вызывает сомнения. Она прекрасно подходит для описания больших массивов данных, равнин как и для характеристики небольшого числового ряда.

Гистограмм называют двухмерный график, по горизонтальная ось который откладываются переменные или числовых интервалов, а по вертикальность – частота возникновения переменная (в заданном интервале). Чаще всего гистограмма составляют из прямоугольников с шириной, равной величине интервала и площадью, которая пропорциональна соответствующая частоте возникновения переменная. Другими сливами, площадь прямоугольнику соответствует количеству значения, попадающих в определенный интервал: чем большее значение, тем больше площадь – при равных значениях интервала, больший столбик будет соответствовать большему количеству значений

Мы коротко рассмотрели определение термина гистограмма, гистограмма в статистике, использование гистограмм. Оставляйте свои комментарии или дополнения к материалу.

Источник

Конспект курса «Основы статистики»

1. Введение

Способы формирования репрезентативной выборки:

Простая случайная выборка (simple random sample)

Стратифицированная выборка (stratified sample)

Групповая выборка (cluster sample)

Типы переменных:

непрерывные (рост в мм)

дискретные (количество публикаций у учёного)

Ранговые (успеваемость студентов)

Гистограмма частот:

Позволяет сделать первое впечатление о форме распределения некоторого количественного признака.

Описательные статистики:

Меры центральной тенденции (узкий диапазон, высокие значения признака):

( используется для среднего значения из выборки, а для генеральной совокупности латинская буква )

Свойства среднего:

Если к каждому значению выборки прибавить определённое число, то и среднее значение увеличится на это число.

Если к каждому значению выборки прибавить определённое число, то и среднее значение увеличится на это число.

Если для каждого значения выборки, рассчитать такой показатель как его отклонение от среднего арифметического, то сумма этих отклонений будет равняться нулю.

Меры изменчивости (широкий диапазон, вариативность признака):

При добавлении сильно отличающегося значения данные меняются сильно и могут быть некорректные.

Дисперсия генеральной совокупности:

(среднеквадратическое отклонение генеральной совокупности)

(среднеквадратическое отклонение выборки)

Свойства дисперсии:

Квартили распределения и график box-plot

Нормальное распределение

Отклонения наблюдений от среднего подчиняются определённому вероятностному закону.

Стандартизация

Правило «двух» и «трёх» сигм

Центральная предельная теорема

Есть признак, распределенный КАК УГОДНО* с некоторым средним и некоторым стандартным отклонением. Тогда, если выбирать из этой совокупности выборки объема n, то их средние тоже будут распределены нормально со средним равным среднему признака в ГС и стандартным отклонением .

30″ alt=»SE = \frac<\sqrt>, n>30″ src=»https://habrastorage.org/getpro/habr/upload_files/20c/135/3bc/20c1353bcfedf2ff8851752cf7f49f37.svg»/>

Доверительные интервалы для среднего

Доверительный интервал является показателем точности измерений. Это также показатель того, насколько стабильна полученная величина, то есть насколько близкую величину (к первоначальной величине) вы получите при повторении измерений (эксперимента).

Идея статистического вывода

2. Сравнение средних

T-распределение

Если число наблюдений невелико и \sigma неизвестно (почти всегда), используется распределение Стьюдента (t-distribution).

Унимодально и симметрично, но: наблюдения с большей вероятностью попадают за пределы от

«Форма» распределения определяется числом степеней свободы ().

С увеличением числа распределение стремится к нормальному.

t-распределение используется не потому что у нас маленькие выборки, а потому что мы не знаем стандартное отклонение в генеральной совокупности.

Сравнение двух средних; t-критерий Стьюдента

Критерий, который позволяет сравнивать средние значения двух выборок между собой, называется t-критерий Стьюдента.

Условия для корректности использования t-критерия Стьюдента:

Две независимые группы

Формула стандартной ошибки среднего:

Формула числа степеней свободы:

Формула t-критерия Стьюдента:

Переход к p-критерию:

Проверка распределения на нормальность, QQ-Plot

Однофакторный дисперсионный анализ

Часто в исследованиях необходимо сравнить несколько групп между собой. В таком случае применятся однофакторный дисперсионный анализ.

Группы:

Нулевая гипотеза:

Альтернативная гипотеза:

Среднее значение всех наблюдений:

Общая сумма квадратов (Total sum of sqares):

Показатель, который характеризует насколько высока изменчивость данных, без учёта разделения их на группы.

Число степеней свободы:

— Межгрупповая сумма квадратов (Sum of sqares between groups)

— Внутригрупповая сумма квадратов (Sum of sqares within groups)

F-значение (основной статистический показатель дисперсионного анализа):

При делении значения межгрупповой суммы квадратов на число степеней свободы, полученный показатель усредняется.

Поэтому формула F-значения часто записывается:

Множественные сравнения в ANOVA

Проблема множественных сравнений:

Поправка Бонферрони

Самый простой (и консервативный) метод: P-значения умножаются на число выполненных сравнений.

Критерий Тьюки

Критерий Тьюки используется для проверки нулевой гипотезы против альтернативной гипотезы , где индексы и обозначают любые две сравниваемые группы.

Указанные сравнения выполняются при помощи критерия Тьюки, который представляет собой модифицированный критерий Стьюдента:

где — рассчитываемая в ходе дисперсионного анализа внутригрупповая дисперсия.

Многофакторный ANOVA

При применении двухфакторного дисперсионного анализа исследователь проверяет влияние двух независимых переменных (факторов) на зависимую переменную. Может быть изучен также эффект взаимодействия двух переменных.

Исследуемые группы называют эффектами обработки. Схема двухфакторного дисперсионного анализа имеет несколько нулевых гипотез: одна для каждой независимой переменной и одна для взаимодействия.

Условия применения двухмерного дисперсионного анализа:

Генеральные совокупности, из которых извлечены выборки, должны быть нормально распределены.

Выборки должны быть независимыми.

Дисперсии генеральных совокупностей, из которых извлекались выборки, должны быть равными.

Группы должны иметь одинаковый объем выборки.

АБ тесты и статистика

3. Корреляция и регрессия

Понятие корреляции

Коэффициент корреляции – это статистическая мера, которая вычисляет силу связи между относительными движениями двух переменных.

Принимает значения [-1, 1]

— показатель силы и направления взаимосвязи двух количественных переменных.

Знак коэффициента корреляции показывает направление взаимосвязи.

Коэффициент детерминации

— показывает, в какой степени дисперсия одной переменной обусловлена влиянием другой переменной.

Равен квадрату коэффициента корреляции.

Принимает значения [0, 1]

Условия применения коэффициента корреляции

Для применения коэффициента корреляции Пирсона, необходимо соблюдать следующие условия:

Сравниваемые переменные должны быть получены в интервальной шкале или шкале отношений.

Распределения переменных и должны быть близки к нормальному.

Число варьирующих признаков в сравниваемых переменных и должно быть одинаковым.

Коэффициент корреляции Спирмена

Регрессия с одной независимой переменной

Уравнение прямой:

— (intersept) отвечает за то, где прямая пересекает ось y.

— (slope) отвечает за направление и угол наклона, образованный с осью x.

Метод наименьших квадратов

Формула нахождения остатка:

— остаток

— реальное значение

— значение, которое предсказывает регрессионная прямая

Сумма квадратов всех остатков:

Параметры линейной регрессии:

Гипотеза о значимости взаимосвязи и коэффициент детерминации

Коэффициенты линейной регрессии

Коэффициенты регрессии (β) — это коэффициенты, которые рассчитываются в результате выполнения регрессионного анализа. Вычисляются величины для каждой независимой переменной, которые представляют силу и тип взаимосвязи независимой переменной по отношению к зависимой.

Коэффициент детерминации

— доля дисперсии зависимой переменной (Y), объясняем регрессионной моделью.

— сумма квадратов остатков

— сумма квадратов общая

Условия применения линейной регрессии с одним предиктором

Линейная взаимосвязь и

Нормальное распределение остатков

Регрессионный анализ с несколькими независимыми переменными

Множественная регрессия (Multiple Regression)

Множественная регрессия позволяет исследовать влияние сразу нескольких независимых переменных на одну зависимую.

Требования к данным

линейная зависимость переменных

нормальное распределение остатков

проверка на мультиколлинеарность

нормальное распределение переменных (желательно)

Источник