для чего нужна таблица пифагора
Удивительные последовательности в таблице Пифагора
Статья написана по мотивам курса на математическом отделении Летней экологической школы (ЛЭШ).
Все когда-то учились умножать (а кто-то, может, и сейчас учится) и наверняка видели таблицу Пифагора. В учебниках её часто рисуют размером 10×10, хотя можно продолжать таблицу до бесконечности.
На первый взгляд кажется, что в таблице Пифагора нет ничего интересного — число в строке умножается на число в столбце и результат пишется в соответствующую клетку. Стало быть, нетрудно догадаться, на сколько различаются соседние числа в каждом столбце или строке (ответ: на номер соответственно строки или столбца).
Из построения таблицы Пифагора ясно, что N-е число в этой последовательности равно N · (N + 1), или N 2 + N. Иначе говоря, N-е число на второй диагонали больше N-го числа на главной диагонали ровно на N:
Оно и понятно — ведь такие два числа стоят в одной строке.
А что, если взять диагональ, перпендикулярную главной? Например, проходящую через число 100 (на рисунке она закрашена синим).

Посмотрим на числа, которые лежат на этой диагонали справа сверху от 100 (они совпадают с теми, что лежат слева снизу): 99, 96, 91, 84.
Какая тут закономерность? Попробуем сравнить эти числа с сотней:
Хорошо. Возьмём ещё одно число, например, 50. Проведём через него диагональ, перпендикулярную главной. Выберем самое большое число на диагонали. Стоп! Да их там аж два: 56 и 56. Стоят рядышком, оба посередине, и ни одно из них не квадрат. Что делать в такой ситуации и как такое вообще вышло?
До этого нам попадались диагонали, у которых есть среднее число, оно же и самое большое — это диагонали, в которых нечётное число клеток. А вот у диагонали с чётным числом клеток посередине не одно число, а пара равных чисел. У нас сейчас именно такая диагональ.
А что, если всё-таки проделать для неё ту же операцию, что и с предыдущими диагоналями? Посмотрим на разность самого большого числа на диагонали (56) и следующих за ним чисел (движемся снова вправо и вверх):
Ничего себе! Вы наверняка уже заметили, что это числа из зелёной диагонали первого рисунка. Догадались, почему?
Задачи для самостоятельного решения
1. Проведём в таблице Пифагора любую диагональ, перпендикулярную главной. Докажите, что числа на ней — это все возможные значения площади прямоугольника с целыми сторонами и определённым периметром. Чему равен этот периметр?
2. Возьмём число N на главной диагонали. Прибавим к нему все числа этой диагонали, стоящие слева сверху, и все числа перпендикулярной диагонали, проходящей через N, стоящие справа сверху (как на втором рисунке). Что получится?
3. (Сергей Прика). В таблице Пифагора выделили прямоугольную рамку толщиной в одну клетку, причём каждая сторона рамки состоит из нечётного числа клеток. Клетки рамки поочередно раскрасили в два цвета — жёлтый и зелёный. Докажите, что сумма всех чисел в жёлтых клетках равна сумме чисел в зелёных клетках.
Таблица умножения: поможем выучить легко и быстро
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Берем табличку Пифагора
Умножение — это легкий и быстрый способ провести вычисления. Чтобы запомнить таблицу умножения за один день, нам поможет другая таблица, которую придумал великий Пифагор.
Обычная таблица умножения выглядит так: десять столбиков, в которых поочередно перемножаются все числа от 1 до 10 и зафиксирован результат действия. Независимо от того, в какой класс перешел ребенок — таблица пригодится всегда.
Зазубрить правильные ответы к сотне примеров, конечно, можно, но сложно. В таком виде не получится отследить логические связи и закономерности. Есть более удобный для изучения способ — таблица Пифагора:
Здесь мы видим, как 100 сочетаний из предыдущей таблицы сокращены до 55. Отличный тренажер!
Таблица Пифагора устроена легче, чем может показаться. Берем числа из левого столбика и умножаем на числа из верхней строки. Правильный ответ — на месте их пересечения.
Не стоит торопиться и ожидать от ребенка молниеносных результатов. Начните изучение с колонок 1, 2, 3. Так постепенно ребенок будет готовиться к усвоению более сложной информации.
Вот как можно потренироваться прямо сейчас: дайте ребенку задание нарисовать таблицу и предложите вместе ее заполнить. Проговаривайте счет вслух — это поможет запоминанию.
Запоминаем главное правило таблицы умножения
Важно знать — от перемены мест множителей произведение не меняется. Знание этого правила значительно облегчит восприятие ребенка. Ведь это означает, что нужно выучить не всю таблицу, а только половину.
Обращаем внимание на закономерности
Важно направить внимание на закономерности в таблице. Есть симметрия? Есть повторения? Отлично — замечая детали, фиксируя свои наблюдения, можно легко запомнить таблицу умножения.
До изучения этой темы ребенок наверняка уже знает, как складывать числа. Значит, можно привести простой пример:
2 × 5 — это то же самое, что 2 + 2 + 2 + 2 + 2, то есть пять раз по 2.
Любое число при умножении на 1 остается тем же.
При умножении на 5 полученное число оканчивается либо на 5, либо на 0. Если число четное, результат будет с 0, если нечетное — с 5.
При умножении на 10 результат будет всегда оканчиваться на 0, а начинаться со второго числа в примере.
Результаты умножения на 5 в два раза меньше результатов на 10.
Играем в таблицу умножения
Как выучить таблицу умножения?
Важно повторять пройденный материал — это поможет закрепить знания. Еще один эффективный способ — учить таблицу умножения в игровой форме.
Самая простая игра — карточки. Есть два варианта:
Подготовить карточки с примерами без ответов.
Сделать карточки с ответами, чтобы ребенок мог озвучить, умножение каких чисел даст такой результат.
Можно играть на время, а можно на количество решенных карточек. Если ребенок сможет вслух объяснить свой ход мысли, это поможет вам понять его логику и дать подсказку.
И, конечно, самая классная игра может быть в реальной жизни. Когда пойдете в продуктовый магазин или будете раскладывать клубнику по тарелкам — попросите ребенка помочь вам в нестандартных подсчетах.
А еще можно использовать смешные стишки:
Запомнить надо постараться,
Что дважды девять — восемнадцать.
Один пингвин гулял средь льдин.
Одиножды один — один.
Прогрызли мыши дыры в сыре.
Трижды восемь — двадцать четыре.
Шесть гусей ведут гусят:
Шестью десять — шестьдесят.
Играем в настолку по таблице умножения
Еще один способ быстрее выучить таблицу умножения в игровой форме — это перенести ее в настолку. К примеру, распечатать таблицу и вместе с ребенком сделать фишки.
Правила просты: ребенок кидает кубик и делает столько ходов фишкой по таблице, сколько ему выпадет. Число, на котором он остановится, нужно умножить на 2. Когда ребенок освоит этот уровень, можно усложнить задачу. Умножайте число на 3, 4 и так далее.
Учим таблицу умножения на пальцах
Умножаем на числа после 5
Этот метод, как быстро выучить таблицу умножения, подходит ребенку, который уже освоил простое умножение на числа до 5 и готов к более сложным примерам.
Делимся методом, как выучить с ребенком таблицу умножения за час. Сначала попросите его взглянуть на ладони обеих рук. Пусть он пронумерует пальцы на обеих руках по порядку: 1 — большой палец на левой руке и так далее, пока не закончит на 10.
После этого спросите, какое число он хочет умножить на 9. Когда ребенок выберет его, попросите загнуть палец, которому вы присвоили это число. Все пальцы слева от загнутого будут десятками, а справа — единицами. Останется только сложить их.
Например, возьмем палец №7 — безымянный на правой руке. Слева от него останется 6 пальцев, а справа — 3. Складываем десятки и единицы, получаем 63. Это и есть ответ.
Изучаем таблицу умножения на фокусах
Фокус для детей «Умножаем на 7»
Этот способ покажет, как помочь ребенку самому выучить умножение на 7. Спойлер — просто добавьте в обучение капельку магии. 🔮
Сначала приготовьте несколько игральных кубиков. После этого заинтригуйте ребенка — скажите, что можете предсказать сумму точек на верхних и нижних гранях, сколько бы кубиков он ни выкинул. Даже несмотря на то, что их низ не виден.
Секрет в том, что сумма точек у кубиков сверху и снизу всегда равна 7. Чтобы «предсказать» результат, нужно просто умножить на 7 число кубиков.
Покажите сыну или дочери этот фокус для детей, а после расскажите секрет. Пусть ребенок сам впечатляет друзей и родных, а между тем тренируется умножать на 7.
Таблица умножения Пифагора
Таблица умножения Пифагора известна с древности. Ее создание, как следует из названия, приписывают древнегреческому философу и математику Пифагору и его ученикам.
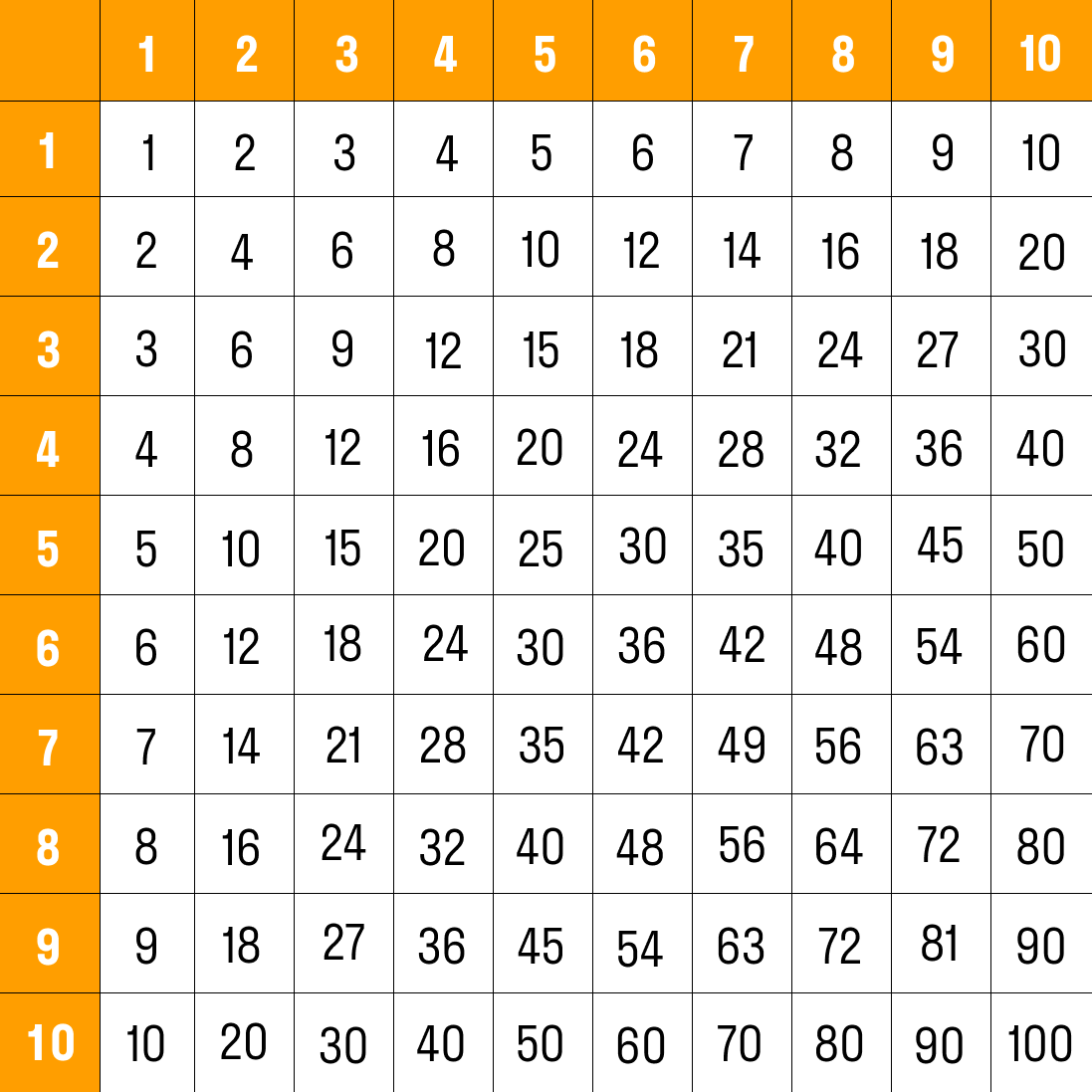
Таблица Пифагора
Таблица умножения Пифагора представляет собой квадрат, на левой и верхней гранях которого расположены числа от 1 до 10, а ячейки содержат результат их перемножения. Размеры таблицы 1-10 не являются конечными, расширить таблицу можно до бесконечности.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
| 1 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 2 | 2 | 4 | 6 | 8 | 10 | 12 | 14 | 16 | 18 | 20 |
| 3 | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 | 27 | 30 |
| 4 | 4 | 8 | 12 | 16 | 20 | 24 | 28 | 32 | 36 | 40 |
| 5 | 5 | 10 | 15 | 20 | 25 | 30 | 35 | 40 | 45 | 50 |
| 6 | 6 | 12 | 18 | 24 | 30 | 36 | 42 | 48 | 54 | 60 |
| 7 | 7 | 14 | 21 | 28 | 35 | 42 | 49 | 56 | 63 | 70 |
| 8 | 8 | 16 | 24 | 32 | 40 | 48 | 56 | 64 | 72 | 80 |
| 9 | 9 | 18 | 27 | 36 | 45 | 54 | 63 | 72 | 81 | 90 |
| 10 | 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 | 90 | 100 |
На главной диагонали, выделенной серым цветом, расположены квадраты чисел, а произведение двух разных чисел находится на их пересечении.
В таблице Пифагора достаточно много закономерностей, на эту тему достаточно много информации в сети. Однако, большая часть данных закономерностей слишком сложна даже для взрослого человека, если рассматривать их практическое применение. Поэтому выделим всего 3 из них:
С помощью этих свойств легче объяснить главный принцип умножения, что, по сути, это многократное сложение. В целом таблица Пифагора хороша в теоретическом плане на начальном этапе, но для практики ее лучше дополнить другими методами, например, логическим.
Таблица умножения Пифагора. Тайны или реальность
Министерство образования и науки РФ
Муниципальное общеобразовательное учреждение
Змеиногорского района Алтайского края
Исследовательская работа по математике
МОУ Саввушинская СОШ
Структура таблицы умножения Пифагора………………….5
Практическое применение таблицы умножения Пифагора.7
Результаты практического применения……………………. 7
Объектная область исследования – математика.
Предмет исследования – структура таблицы умножения Пифагора.
Гипотеза: при условии, что таблица умножения встречается практически на каждой тетради по математике, мы постоянно используем её для решения задач и примеров, применяя заученный алгоритм, не вникая в структуру и не задумываясь, не понимая как она устроена. Мне захотелось выявить какие тайны скрыты в ней и где ещё применяется таблица умножения, а так же провести анкетирование среди учащихся нашей школы, чтобы понять, знают ли историю возникновения таблицы умножения Пифагора ученики нашей школы.
Узнать, является ли Пифагор Самосский автором таблицы умножения. Познакомится со структурой и применением в жизни таблицы умножения Пифагора. Узнать о жизни Пифагора Самосского. Заинтересовать учеников историей возникновения таблицы Пифагора и показать важность знания таблицы умножения.
Теоретический: изучить биографию Пифагора, проанализировать математические энциклопедии, научно – популярную литературу, найти различные источники в сети Интернет.
Эмпирический: провести анкетирование учащихся старшего звена и среднего, с целью выявить знания таблицы Пифагора, биографии ученого, структуру построения и её практическое применение.
Актуальность исследованной проблемы:
Таблица умножения Пифагора – это попросту всем известная таблица умножения, но где и как она возникла, какова ее структура, где еще применяется кроме математики, и является ли Пифагор автором ее – это и стало целью моего исследования.
Эту работу я считаю актуальной потому, что в наше время стали забывать о древних открытиях. И таким способом я решил напомнить об одном из древних достижений, о таблице умножения Пифагора, показать важность знания таблицы.
Ведь это не просто умножение чисел, в ней скрыто много разных тайн. И если кто-нибудь захочет открыть эти тайны, моя работа поможет ему в этом.
Таблица умножения это помощь в получении основных знаний по математике, без которых будет очень сложно освоить такую интересную, но в тоже время и сложную науку, как математика.
определил, как влияют числа на меня и моих родителей. С чем я вас и знакомлю в своей работе.
Биография Пифагора Самосского
Великий древнегреческий ученый Пифагор (580-496гг. до н. э.) родился на острове Самос около 580 года до н. э., по другим источникам, в 586 году до нашей эры. Однако известно, что в 588 году до н. э. Пифагор стал победителем турнира по кулачному бою на Олимпийских играх, тогда впервые включённого в программу соревнований. В молодости побывал в Египте, где учился у жрецов, говорят, что он был допущен в сокровенные святилища Египта, посетил халдейских мудрецов и персидских магов. Родители Пифагора принадлежали к старой аристократии.
Историю его жизни трудно отделить от легенд, представляющих Пифагора в качестве полубога и чудотворца, совершенного мудреца и «великого посвященного» во все тайные доктрины греков и варваров.
По преданию Пифагор объездил весь свет и собрал свою философию из различных источников, к которым имел доступ. Так, например, он изучал эзотерические науки у брахманов Индии, астрономию и астрологию в Халдее и Египте. В Индии он известен под Именем Яваначарья («Ионийский учитель»).
Юный Пифагор отправился в путешествие по следам Фалеса в 540 годы – когда вавилонское царство содрогалось под нажимом новой персидской державы, а греки в Ионии уже подчинялись персам. Вернувшись, домой Пифагор обнаружил, что власть на острове Самос захватил тиран Поликрат – бывший торговец обувью.
Не желая терпеть этого выскочку, Пифагор решил создать независимую республику где-нибудь вдали от восточных царей и греческих тиранов. Такое место нашлось в южной Италии – в маленьком городе Кротон, основанном греками лет за сто до рождения Пифагора. Здесь Пифагор около 535 года до н. э. основал свою школу похожую одновременно на монашеский орден, политическую партию и на шахматный клуб.
Возникновение школы Пифагора оказало большое влияние на становление философии, так как именно в ней был сделан первый шаг от материализма к идеализму. Заслугой пифагорейцев было выдвижение мысли о количественных закономерностях развития мира, что содействовало развитию математических, физических, астрономических и географических знаний. Они создали именно те основы, которые до сих пор, изучают в школах.
Первоначалом, по их мнению, является «число». В основе вещей лежит число, учил Пифагор, познать мир — значит познать управляющие им числа. Изучая числа, они разработали числовые отношения, и нашли их во всех науках — музыке, астрономии и так далее. В сферу интересов членов союза входили научные исследования – религиозные философские изыскания, политическая деятельность. Они вели суровый образ жизни, превыше всего ценили самообладание, смелость и коллективную дисциплину. Пифагорейцы жили вместе, у них было совместное имущество, и даже свои открытия они считали общим достоянием.
Деятельность союза была окружена тайной, поэтому никаких текстов о ранних Пифагорейцах не осталось. Кроме того, все открытия они приписывали Пифагору, о котором уже при жизни ходили легенды. Кто на самом деле является автором того или иного результата, неизвестно.
Пифагорейцы называли собственные исследования «математом», что означает «науки» и делили их на четыре части: арифметику, геометрию, астрономию и гармонию (учение о музыке).
Пифагор проповедовал, что всю природу, всю вселенную, все на свете можно свести к натуральным числам и их отношениям. Одно-единственное математическое противоречие мгновенно разрушило философию и математику Пифагора: невозможно найти два таких целых числа, чтобы квадрат одного из них был вдвое больше квадрата другого.
Тайны, которые окружают Пифагора и его последователей, заставили меня задуматься о простых вещах окружающих нас в повседневной жизни, к моему удивлению оказалось, что очень многих ученных интересовала личность Пифагора.
Доддс считал Пифагора «великим греческим шаманом», который, без сомнения, извлек теоретические выводы из своих экстатических опытов и в результате уверовал в метемпсихоз.
Однако наиболее подробно проанализировал все источники легенды о Пифагоре Беркерт. Он указал на то, что основные ее положения вписываются в единый ритуально-мифологический сценарий, характерный, для легендарных персонажей, перечисленных выше. В самом деле, легенды о Пифагоре говорят, о его связи с богами и духами, приписывают ему власть над животными, сообщают о пребывании одновременно в разных местах. Беркерт объясняет знаменитое «золотое плечо» Пифагора, сравнивая его с шаманской инициацией.
Считалось, что в момент инициации у шаманов Сибири происходило обновление органов, и кости их схватывались железом. Странствования Пифагора сближают его с Эпименидом и Эмпедоклом, которых Беркерт также считал своеобразными «шаманами». Наконец, Катабазис Пифагора также является шаманским элементом. Согласно Иерониму Родосскому, Пифагор спускался в Ад и встречался с душами Гомера и Гесиода, наказанными за злословие в адрес богов. Как вы знаете в третьем классе дети изучают таблицу Пифагора, не вдаваясь в подробности, как она построена, кто её изобрёл и какие ещё тайны она в себе хранит.
Структура таблицы умножения Пифагора
Впервые таблица Пифагора примерно в таком же виде, каком мы ее находим на обложках ученических тетрадей, появилось в сочинениях Никомаха (1-2 вв.).
Числа в каждой строке таблицы Пифагора образуют последовательность чисел составленных определенным образом.
Умножение натуральных чисел есть не что иное, как многократное прибавление к сумме одного и того же слагаемого.
Таблица Пифагора симметрична относительно диагонали, ведущей из левого верхнего угла в правый нижний. Данное свойство – геометрическая иллюстрация свойства умножения.
Цифры в первом столбце и последние цифры в девятом столбце повторяют друг друга, но идут в обратном порядке. Этим свойством обладают последние цифры второго и восьмого столбцов; третьего и седьмого, четвертого и шестого. Я сделал открытие: для произвольных двух цифр А и В последняя цифра произведения АВ равна последней цифре произведения (10-А)*(10-В), так как разность чисел АВ и (10-А)*(10-В) делится на 10. Рассмотрим некоторые факты: назовем квартетом четыре числа таблицы Пифагора расположенные в вершинах некоторого квадрата, а числа стоящие на диагонали таблицы – диагональными.
Оказывается, если стороны этого квадрата параллельны диагоналям таблицы Пифагора, то суммы диагональных чисел квартета равны. Если стороны квадрата параллельны сторонам таблицы, то равны произведения диагональных чисел квартета. Если при этом квадрат расположен симметрично главной диагонали таблицы Пифагора, то суммы всех чисел квартета – квадрат некоторого натурального числа.
Таблица умножения Пифагора[1]