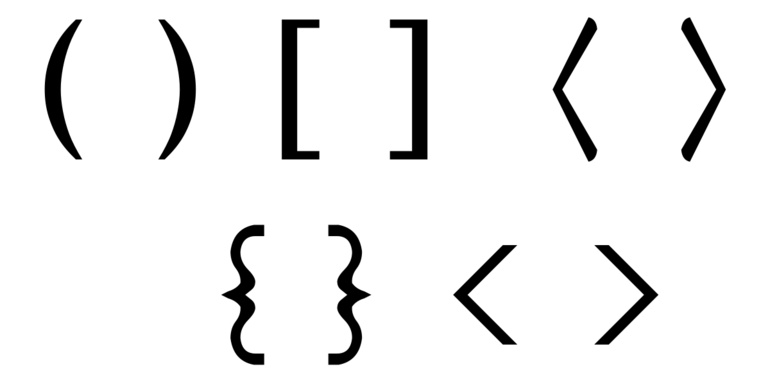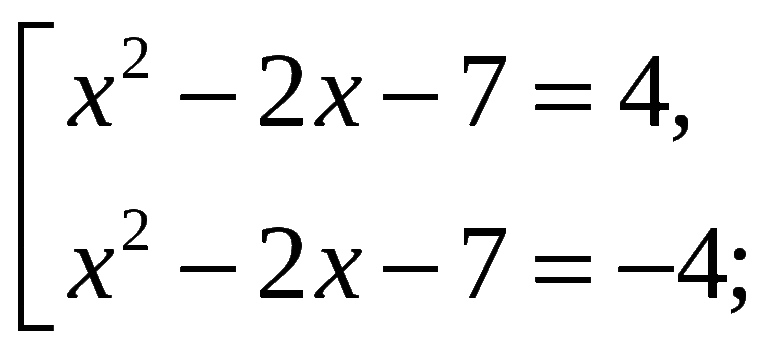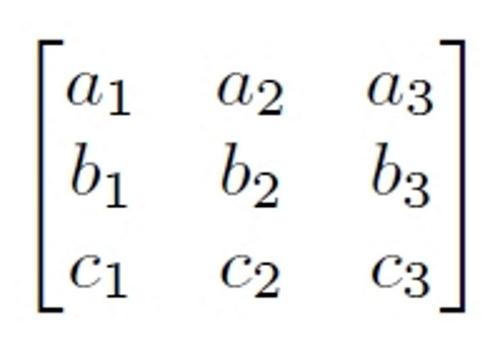для чего нужны квадратные скобки

О квадратных скобках

Сегодня мы поговорим о квадратных скобках и их правильном использовании.

Историческая справка

Когда-то мониторы были плохими, и графические режимы были для них страшным мучением. Как правило, мониторы переключались из текстового режима в графический не совсем мгновенно, экран при этом неприятно мигал. Использование разработчиками графического режима без острой необходимости (то есть, не для отображения рисунков, схем или графиков) вызывало у пользователей раздражение. Операционной системой на компьютерах простых смертных стоял MS-DOS, где подавляющее большинство программ работали в текстовом режиме, 80×25 строк.

Однако даже в текстовом режиме разработчики пытались изображать в своих программах какие-то элементы графического интерфейса: окна, меню и кнопки. А чтобы их изобразить, нужны были рамочки.

В качестве дешёвого способа нарисовать рамочки таблица ASCII предлагала псевдографику — набор символов, представляющих собой всевозможные края одинарных и двойных рамочек, а также стыковок между ними:

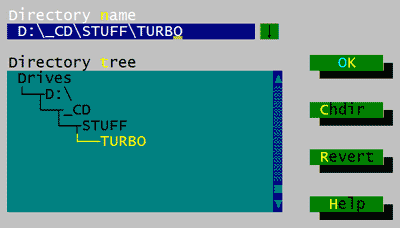
Программы, интерфейс которых был построен на библиотеке Turbo Vision (среди них DOS Navigator, Turbo Pascal 6-й и 7-й версий), пользовались псевдографикой с особым размахом, умудрясь рисовать объёмные кнопки:

Когда кнопку нажимаешь, она действительно нажимается.

Некоторые разработчики ленились использовать псевдографику, и прибегали к ещё более дешёвому способу изобразить кнопку — поставить квадратные скобки и написать между ними название:

В текстовом режиме, из-за того, что все символы имеют одинаковую ширину и высоту, экран воспринимается такой матрицей, где квадратные скобки (как и всё остальное) занимают свои ячейки. Поэтому недостающие верхняя и нижняя рамки как бы дорисовываются пользователем уже подсознательно. Конечно, вариант из Turbo Vision воспринимается лучше, но этот тоже можно терпеть.

Квадратные скобки в русском языке

На самом деле, квадратные скобки придумали совсем не для того, чтобы дешёвые кнопки рисовать в DOS’е, и даже не для того, чтобы индексы массивов указывать в языках программирования. Квадратные скобки, как и круглые скобки, точки, запятые, знаки восклицательный и вопросительный, многоточия, тире, и многое другое, являются пунктуационными знаками русского языка (и не только русского, конечно). Квадратные скобки используются, во-первых, как скобки второго уровня, по аналогии с «кавычками „лапками“», и, во-вторых, при цитировании.

При цитировании они могут использоваться для пояснений:

А вот на большее, вот этих самых ребят не хватает. [С пафосом] Но они базис. вот этого самого. прекрасного действа под названием супер-игроки, современные супер-игроки в снукер.

(Приведён кусок из заметки про Сашу Елисейкина, где квадратные скобки используются мной по назначению.)

А ещё они могут указывать на отклонение от оригинала:

Как видим, квадратные скобки — это не рамочки, которыми нужно ограничивать кнопки.

Квадратные скобки в сегодняшнем вебе

Сегодня в вебе квадратные скобки используются как угодно, только не по назначению. Больше всего в них любят заключать пункты меню:

Их используют тупо как первый подвернувшийся под руку разделитель, видимо, помня, что где-то такое использование уже видели. При этом не учитывается, что в графическом режиме эффекта «матрицы», о котором шла речь выше, не создаётся, и поэтому это совершенно не похоже на кнопку. Когда ссылки, заключённые в квадратные скобки, ещё и подчёркивают, становится и вовсе страшно: линия подчёркивания не совпадает по высоте с уголками квадратных скобок, и, кроме того, начинает ещё острее ощущаться отсутствие такой же линии сверху. А особый вид извращения — это взять кнопку в квадратные скобки, подчеркнуть и при этом выделить курсивом.

Такие «кнопки» выглядят неряшливыми, сделанным «на коленке» за полторы минуты.

Уже во времена DOS была возможность нарисовать кнопку более натурально, чем с помощью квадратных скобок — и разработчики Turbo Vision этим успешно пользовались, — что уж говорить о сегодняшнем дне. Даже в Photoshop ходить не надо, CSS всегда под рукой. Возьми и сделай кнопку, раз так хочется!

А ещё лучше подумать, нужен ли вообще этот закос под кнопки, или всё же не выпендриваться, а сделать просто нормальные текстовые ссылки.

Источник

Общая характеристика

Главная задача знаков — описание этапов осуществляемых действий. Математическое уравнение или выражение имеет одиночную пару квадратных, фигурных и других скобок, а также может использовать их некоторое количество.

Значение и разновидности

Скобки — это парные знаки, используемые во всевозможных областях. Чтобы правильно выстроить фразу в русском языке, для понимания смысла текста в предложении они употребляются как знаки препинания. С начальных классов школы изучают основы этих знаков.

В расчетах первая из скобок считается открывающей, а вторая — замыкающей. Оба знака соответствуют друг другу, но также используются те, в которых открытие или закрытие не различается (косые /…/, прямые скобки |…|, двойные прямые ||…||. Раскрывать значение можно чаще всего в математике, физике, химии и остальных науках для указания важности выполнения операции в формулах. На компьютерной клавиатуре представлены все виды знаков препинания.

Разновидности:

Открытие круглых () произошло в 1556 году для подкоренного выражения. По правилу первым выполняется действие внутри знака, затем произведение или определение частного (деление), а в конце — суммирование и разница.

В Microsoft word, Excel включена электронная конфигурация этих знаков. Часто используемые виды скобок, следующие: (), [ ], < >(), [ ], < >. Также встречаются двойные, называемые обратными (]] и [ [) или > в виде уголка. Их использование является двойственным — с открывающейся и замыкающей скобочкой.

Основные цели квадратной скобки в математике:

Другие варианты расчета:

Квадратные скобки в математике обозначают, что действие выполняется последовательно. Эти знаки позволяют разграничить операции.

Треугольные актуальны в теории групп. Правило записи ⟨ a ⟩ n характеризует циклическую группу порядка n, сформированную элементом a.

Круглые (операторные) () используются в математике для описания первостепенности действий. Например, (1 +5)*3 означает, что нужно сначала сложить 1 и 5, а затем полученную величину перемножить на 3. Наряду с квадратными, используются для записи разных компонент векторов, матриц и коэффициентов.

На уроке математики преподаватель объясняет, как раскрыть скобки в уравнении для последующего решения. Фигурная одинарная < встречается при решении систем уравнений, обозначает пересечение данных, а [[ используется при их слиянии.

Одинарные или двойные выражения

Употребление [] происходит реже. Одно уравнение со скобками объединяет несколько значений или неравенств различных размеров. Для решения совокупности нужно выполнить любое условие. Конец, завершение действия замыкает закрывающий знак.

В персональных компьютерах, ноутбуках, нетбуках встроена кодировка Юникод, закрепленная не за левыми или правыми объединяющими знаками, а за открывающими и замыкающими, поэтому при воспроизведении печатного текста со скобочками в режиме «справа налево» каждый знак меняет внешнее направление на обратное.

Квадратные скобки в уравнении означают, что установлен порядок действий, задаются границы промежутков и необходимость выполнения действия над выражением. Двойные квадратные скобки необходимы для записи выражений наряду с круглыми для рационального порядка действий.

По правилам интервал [−a;+a] записывается в виде нестрогого неравенства −a≤x≤a, означающего, что x находится на промежутке от −a до a включительно.

В середине парного знака с отделяющей точкой или запятой указываются два числа — наименьшее, затем большее, ограничивающие интервал. Круглая скобочка, прилегающая к цифре, означает невключение числа в промежуток, а квадратная — добавление.

В некоторых учебных пособиях для вузов встречаются расшифровки числовых интервалов, в которых вместо круглой скобочки (применяется обратная квадратная скобка ], и наоборот. В обозначениях запись ]0, 1[ равносильна (0, 1).

Открытая квадратная скобка (символ [) значит, что совокупность представляет систему уравнений разных размеров, для которых справедливы все множества решений для каждого уравнения, входящего в общее задание. Например, [x+11=2yy2−12=0

Прежде чем решать задачу или выполнять задание, нужно правильно определить принципы действий. В некоторых случаях скобочки могут быть не нужны, а иногда их обязательно нужно поставить.

Прочие знаки

Для математических, алгебраических и прочих расчетов важно знать различие обобщающих знаков. От правильности вычислений зависит итоговый результат.

Удобство записи системы уравнений

Применение фигурных знаков относится к представлению совмещения множеств. При решении системы с фигурной скобкой уравнения пересекаются, а [] объединяет их.

Источник

Про скобки в русском языке

Рассмотрим правила употребления круглых и квадратных скобок в русском языке.

Скобки являются двойным знаком препинания, в который заключаются поясняющие или дополняющие высказываемую мысль слова и предложения. Первая скобка — открывающая, вторая — закрывающая. В русском языке чаще всего используют круглые ( ) и квадратные скобки [ ]. На правилах их употребления мы подробно и остановимся в этой статье.

Круглые скобки

Круглые скобки в русском языке используются для выделения пояснительных, уточняющих, дополняющих конструкций. Так, в скобках может заключаться уточнение значения отдельного слова, даваться попутное указание для разъяснения смысла фразы, указываться авторское замечание, дополнение высказываемой мысли. Такими вставными конструкциями могут быть как отдельные слова, так и целые предложения, и находиться они могут в середине или в конце предложения. По тому, насколько верно копирайтер использует типографские знаки в тексте, к которым относятся скобки (а также тире, кавычки, многоточие), можно судить об уровне его профессионализма.
Рассмотрим основные значения вставных конструкций и примеры их использования:

1) Дополнение содержания высказывания. Например:

В один прекрасный день (это было в прошлом году) мне позвонил с работы муж.

В 1976 году я наконец получила диплом по бухгалтерскому делу (я с отличием закончила Флоридский университет) и мечта моих родителей осуществилась.

2) Пояснение или уточнение части высказывания или отдельных слов. Например:

Орегано отлично дополняет блюда из мяса (особенно баранину).

Цезарь (так звали льва в зверинце) спит и тихо взвизгивает во сне.

Село Новосельское (мы говорим о Новокубанском районе) расположено среди распаханных полей.

3) Пояснение мысли высказывания в целом. Например:

Я заплатил наличными пять тысяч за дом, стоивший мне сорок пять тысяч (на самом деле его цена была шестьдесят пять, но никто не хотел его покупать).

4) Добавочное авторское замечание, восклицание или вопрос. Например:

Охотники (а их немало в этом краю) чувствуют себя гостями в лесу (В. Тендряков).

Время (дело известное) летит иногда птицей, иногда ползет червяком; но человеку бывает особенно хорошо тогда, когда он даже не замечает – скоро ли, тихо ли оно проходит (И. Тургенев).

Однажды, проснувшись ночью в своем доме в пригороде по уши в долгах (воплощение американской мечты), они говорят себе: «Мои финансовые проблемы можно решить, если найти способ быстро разбогатеть» (Р. Кийосаки).

Помимо этого, круглые скобки используются:

1) Для ремарок в стенограммах речей, выступлений, докладов, обращений. При этом перед закрывающей скобкой в конце ремарки ставится точка, а точка и вопросительный/восклицательный знак перед открывающей скобкой сохраняются. Например:

На этом мой доклад заканчивается. Уверен, человечество сможет преодолеть эти трудности! (Все встают. Аплодисменты.)

Печать издания откладывается. (Редакция.)

2) Для ремарок в драматическом тексте. Например:

Я только поклонюсь вам и тотчас же уйду. (Горячо целует руку.) Мне приказано было ждать до утра, но у меня не хватило терпения.

3) Для указания источника цитирования или имени автора и названия произведения, из которого взята цитата. Например:

«Вы все отрицаете, или, выражаясь точнее, вы все разрушаете… Да ведь надобно же и строить. » (И. С. Тургенев. Отцы и дети). Заглавие источника отделяется точкой от фамилии автора и не заключается в кавычки.

«Знаки препинания — это как нотные знаки. Они твёрдо держат текст и не дают ему рассыпаться» (К. Г. Паустовский).

4) В маркированных списках может использоваться закрывающая круглая скобка. Например:
1); а).

Знаки препинания до скобок

По правилам русского языка, перед открывающей и закрывающей скобкой знаки препинания не ставятся. Это относится к запятой, точке с запятой, тире, двоеточию. Постановка данных пунктуационных знаков возможна только после закрывающей скобки. Например:

Вся эта стройка (как позже выяснилось) — дедушкина затея.

Перед закрывающей скобкой могут стоять вопросительный или восклицательный знак, многоточие, точка. Например:

Сегодня отличная погода (наконец-то дождя нет!)

Между тем лесок (какой там лесок — осиновые кустики!) начал смутно проступать.

Знаки препинания после скобок

После закрывающей скобки ставится такой знак препинания, который необходим по условиям предложения, при этом не имеет значения, какой знак находится до закрывающей скобки (вопросительный, восклицательный, многоточие или точка). Например:

Неверие — в греческом языке означает не только «недоверчивость» (что мы называем скепсисом, когда, например, говорим об атеизме), но и нежелание соблюдать договоренности хотя бы и устные.

Квадратные скобки в русском языке

Квадратные скобки в предложении ставятся при цитировании. В них заключают текст автора, который призван прояснить контекст цитаты. Например:

«Их [детей] было семеро».

Также квадратные скобки применяются при оформлении библиографических списков.

Как поставить квадратные [скобки] на клавиатуре

Символы квадратных скобок находятся на буквенной клавиатуре. Открывающая скобка расположена на русской букве «Х», а закрывающая — на букве «Ъ». Поставить квадратные скобки очень легко: нужно в английской раскладке нажать на клавиши с соответствующим обозначением.

Источник

Где расположена квадратная скобка на клавиатуре? Варианты использования и набора символов

Наиболее часто квадратная скобка используется в различных формулах. Это может быть, например, математический расчет, физическая или же химическая формула. Также такой символ используется при транскрипции английских слов. В этом материале будет изложен порядок его набора в различных видах программного обеспечения.

Когда используется?

Наиболее часто, как было отмечено ранее, данный символ используется при наборе формул. Например, при оформлении математических вычислений с его помощью можно сгруппировать различные элементы и определить приоритет выполнения вычислений. Аналогичным образом его можно применить и в физических уравнениях. При этом в химии его появление позволяет выделить сложное вещество.

Вам будет интересно: Нововведения в браузере «Интернет Эксплорер 11»

Но не только в составе формул можно встретить рассматриваемый элемент. Например, слова в квадратных скобках записываются при фонетической транскрипции выражений на английском языке.

Также нередко такую скобку можно встретить и в программном коде. Она позволяет переопределить порядок расчетов. В некоторых случаях она может входить в состав оператора, а в другой среде разработки организовывает ввод комментария.

Отдельно нужно отметить еще и тот момент, что данный символ является парным. То есть если введена левая открывающая скобка, то и правая должна находиться далее по тексту. В противном случае теряется смысл использования таких элементов.

Возможные способы набора

Квадратная скобка на компьютере может быть получена следующими способами:

Каждый из этих способов будет в дальнейшем детально рассмотрен. Также будут указаны их преимущества и недостатки. В дополнение к этому будут даны рекомендации относительно их использования.

Используем клавиатуру

Квадратные скобки на клавиатуре стандартных размеров находятся в правом верхнем ее углу. Справа от них выведена клавиша Enter, а слева – привычные буквы. Ввести данный символ можно только при включенной латинской раскладке. В русской же левой квадратной скобке соответствует буква «х», а правой – «ъ». Поэтому для их набора необходимо перейти в английский язык.

Алгоритм набора квадратных скобок в этом случае такой:

С применением ASCII-кода. Порядок набора

Теперь разберемся с тем, как сделать квадратные скобки на клавиатуре с использованием специальных кодов. В данной ситуации порядок ввода такой:

С практической точки зрения данный метод не совсем удобен. При его использовании необходимо помнить множество специальных кодов.

Буфер обмена

Еще один универсальный способ набора – это буфер обмена. При его использовании пользователь должен совершить такие действия:

Редактор формул Word

Теперь разберемся с тем, как поставить квадратные скобки в системе набора наиболее популярного текстового редактора на сегодняшний день. В этой ситуации порядок действий следующий:

Заключение

В данном материале были рассмотрены основные случаи использования таких символов, как квадратные скобки. Также приведены алгоритмы их набора или же копирования. При этом на практике наиболее удобно использовать английскую раскладку клавиатуры. В этом случае нет нужды помнить специальные коды или же копировать символ из браузера в буфер обмена. Единственное исключение – редактор формул текстового процессора Word. В этом случае лучше всего использовать специальную панель и манипулятор.

Источник

Как репетитор по математике оформляет объединение систем

Системы уравнений и неравенств входили в состав выпускных и вступительных экзаменов по математике во все времена. Даже если в экзаменационном варианте нет прямого задания на решение системы, то существует достаточно высокая вероятность ее появления процессе решения других задач. Репетитор по математике обязан это учитывать. Привести к системам могут задачи на модули, на логарифмы, на графики и даже на синусы с косинусы. Несмотря на то, что подготовка к ЕГЭ по математике нередко сводится к натаскиванию на решение однотипных номеров части «В», не стоит полностью отказываться от тренировки навыков поиска пересечения (объединения) ответов разных объектов. Хотя бы на элементарном уровне. Какими приемами репетитор по математике обеспечивает оптимальную работу ученика с системами? Какая техника оформления систем была бы самой удобной и продуктивной?

К сожалению, школьные учителя и даже некоторые профессиональные репетиторы требуют от детей (уже в 8 классе) оформление систем по принципу «все в одном», упаковывая содержащиеся в них неравенства в единый объект согласно строгим правилам проведения равносильных преобразований. Широко применяются квадратные и фигурные скобки, причем часто в весьма сложном сочетании. Мой опыт репетиторской работы свидетельствует о том, что дети с огромнейшим трудом воспринимают, казалось бы, несложные для математиков логические конструкции с конъюнкциями и дизъюнкциями. Примерно 60-70% всех школьников с трудом припоминают (или не знают вообще) чем отличается квадратная скобка от линейной. А среди тех, кто приходит к репетитору по математике, этот процент повышается в среднем до 90-95%.

Но, тем не менее, для обозначения объединения, некоторые школьные преподаватели все равно используют квадратные скобки. Видимо по привычке. При таком раскладе репетитор по математике оказывается в крайне сложном положении, ибо уровень ученика часто не позволяет осознать сложные логические сочетания. Я не сторонник любой ценой следовать школьным стандартам и часто полностью отказываюсь от постановки квадратных скобок. Без них проще. Особенно когда на носу подготовка к ЕГЭ. Если все же репетитор математики вынужден принимать школьные правила, он мог бы это сделать следующим образом:

Когда репетитор по математике вводит квадратную скобку?

Как видите, используется самое простое сочетание. Скобку лучше всего ввести после того, как ученик поймет суть задания. А она заключается в том, чтобы подобрать числа, обеспечивающие выполнение хотя бы одного неравенства (я употребляю общий термин: «условие»). Фразу «хотя бы одного» репетитор по математике сразу же меняет на фразу «или одно или другое». Процент учеников, правильно нашедших репетитору ответ, оказывается не таким и уж низким. Половина детей схватывают суть задания сразу же. Другим нужно показывать, как проверяется наугад взятое число (главное не объяснять только словами).

Данный номер рассматривается репетитором сразу после примера на совокупность, то есть на поиск числа, обеспечивающего выполнение каждого условия:

К сожалению, родители редко приглашают репетитора по математике в 8 классе и подготовкой к ЕГЭ занимаются только с 10 или с 11 класса. В этом случае репетитору приходится объяснять оформление объединения по формальному признаку фигурной скобки: если для проверки произвольно взятого числа достаточно проверить верность одного из нескольких условий (неравенств, уравнений или их систем), то проверяемые объекты можно заключить в квадратную скобку. Корректируя общую формулировку, репетитор по математике вставляет в нее союз «или». Например, для того, чтобы число x было корнем уравнения необходимо чтобы или первый множитель равнялся нулю, или второй. Преподаватель отдельно акцентирует внимание ученика на участии «или» и в случае его уместного употребления разрешает заключить объекты в квадратную скобку.

Если репетитор математики примет строгое оформление, он усложнит ученику одновременно и понимание и практическую работу. Школьные учителя берут за образец оформление систем в задачниках, в которых решения излагаются кратко. Из-за пропусков некоторых его частей удается компактно расписать все равносильные переходы, сохраняя целостность объекта. Репетитору по математике данная методика не подходит категорически. Почему? Ученики начинают вырывать по отдельности неравенства из огромной системы через весьма приличные промежутки времени. Переключение внимания на частные операции сбивает школьников с главного направления. Они забывают что именно им надо пересекать, а что объединять. Путаница возникает страшная. Хорошо, если репетитор по математике рядом и сможет подсказать. А что делать на ЕГЭ? Вряд ли стоит рисковать. Техника действий должна быть максимально прозрачной и удобной в практическом смысле.

Принимая квадратную скобку, репетитор по математике усложняет еще и сортировку решенного. Приходится оформлять отдельные неравенства в колонку (одно под другим) и запоминать какое именно решено, а какое еще нет. Если сами решения длинные, то ученику может не хватить страницы и придется ее переворачивать. Рассеивание внимания при этом гарантировано.

Может ли репетитор по математике обойтись без квадратной скобки

Да, вполне. Для этого применяются стрелочный эквивалент. Например:

Чаще всего в объединение попадают две системы (если больше — лучше использовать иные методы изначально). В нашем случае одна из систем решается в левой части тетрадного листа, а другая в правой. Репетитор по математике разделяет квадратную скобку на две совокупности отдельных систем. На мой взгляд, это самая удобная форма для практической работы ученика. Почему? Те ответы, которые нужно пересечь, распределены по колонкам, при этом операции в левой и в правой колонке проводятся локально и не перемешиваются. Слева — свое пересечение, справа — свое. Очень удобно. Под каждой системой – решение. Системы не нужно вырывать из «квадратной скобки», не нужно переписывать. Финальные ответы, которые репетитор по математике и ученик получают слева и справа «сваливаются в общий ответ» без какой-либо коррекции и пересечения.

Исключение составляют случаи, когда промежутки имеют общую часть. Однако практика показывает, что даже если репетитор по математике забудет напомнить о «склеивании частей», то большинство учеников догадаются до него сами.

Преимущество стрелок для запоминания:
Когда ученик разделяет тетрадный лист на две части, то находясь на любом этапе решения по левой колонке, он помнит о том, что предстоит еще заполнить и правую часть. Это очень важно. Если вы репетитр, то наверняка знаете, что школьники часто забывают разобрать какой-нибуь случай или решить какое-нибдуь неравенство из системы.

Сложность работы с объединением и пересечением носит часто чисто технический характер и связана с проблемой механики решений, то есть запоминанием и сортировкой обрабатываемой информации. При подготовке к ЕГЭ по математике важно получить навык автоматического выполнения операций. Поэтому репетитору по математике крайне необходимо использовать в работе простые и удобные методы, каким является прием стрелочного разделения. Если потребуется объединить три или более системы, репетитор по математике может взять лист формата А4, развернуть его в длину и аккуратно решить задание распределяя системы по нескольким колонкам. Такой подход к оформлению позволит ученику четко разделить и запомнить логическую структуру объекта.

Репетитор по математике, Колпаков А.Н. Москва.

Источник