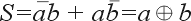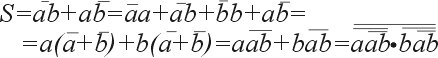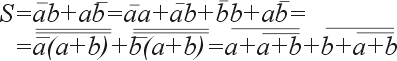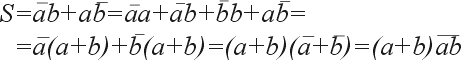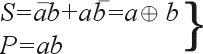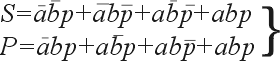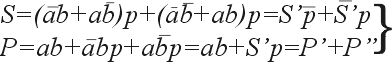для чего нужны сумматоры
Принцип работы сумматора
Сумматоры. Устройство, принцип работы
Сумматоры — это комбинационные устройства, предназначенные для сложения чисел.
Функционирование однозарядного сумматора показано в таблице, приведённой на рис.10.30. В этом случае при сложении слагаемых используется перевод десятичных чисел в двоичные числа.
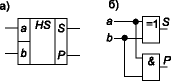
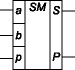
Pиc.10.29. Символическое изображение одноразрядного двоичного сумматора
При сложении слагаемых или 0+1+0 получается десятичное число 1. Такому числу соответствует двоичное число 01, при этом Аналогично, 1+1+0 = 2, которому соответствует двоичное число 10, при этом . При сложении чисел 1+1+1 = 3, которому соответствует двоичное число 11, при этом и так далее.
Сумматоры могут быть последовательного и параллельного действия. В сумматорах последовательного действия коды двоичных чисел вводятся в последовательной форме слагаемое за слагаемым, начиная с младшего разряда.
На рис.10.31 изображена схема сумматора последовательного действия, предназначенного для суммирования четырёхразрядных двоичных чисел. Сумматор построен на трёх регистрах сдвига, D-триггере и на одноразрядном сумматоре.
Рис.10.30. Таблица функционирования одноразрядного сумматора
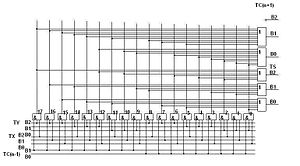
Рис.10.31. Схема сумматора последовательного действия
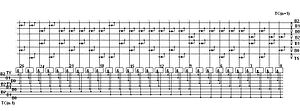
Функционирование сумматора приведено в таблице рис.10.32, где слагаемое pi для первого разряда всегда равно нулю.
Рис.10.32. Таблица функционирования сумматора
Для ускорения операции сложения используются сумматоры параллельного действия, которые состоят из нескольких однозарядных сумматоров. В таких сумматорах слагаемые поступают одновременно на соответствующие входы однозарядных сумматоров, при этом каждый из однозарядных сумматоров формирует на своих выходах суммы соответствующих разрядов и слагаемые переноса, передаваемых на входы старших разрядов. Схема четырёхразрядного сумматора параллельного действия приведена на рис.10.33.
Рис.10.33. Схема четырёхразрядного сумматора параллельного действия
Что такое сумматор
В общем смысле слова, сумматор – это какое-либо устройство, которое что-либо суммирует и выдает на выходе сумму этих воздействий. Сумматор можно представить в виде какого-либо неизвестного нам ящика, на который поступает входные воздействия и на выходе такого ящика выдается их сумма.
В электронике сумматоры делятся на две группы:
В этой статье мы будем разбирать аналоговые сумматоры.
Аналоговый сумматор
Многие помнят осциллограмму постоянного напряжения.
Если, допустим, цена нашего квадратика 1 В, то на данной картинке мы видим постоянное напряжение амплитудой в 1 В. Суммировать постоянное напряжение – одно удовольствие. Для этого достаточно сложить амплитуды этих сигналов в любой момент времени.
На рисунке ниже мы видим два сигнала A и B и сумму этих сигналов: A+B. Если сигнал A = 2 В, сигнал B = 1 В, то сумма этих сигналов составит 3 В.
Все то же самое касается и сигналов с отрицательной полярностью.
При сложении сигналов с равной амплитудой, но разной полярности, в сумме получаем 0. То есть эти два сигнала взаимно себя скомпенсировали: 1 +(-1)=0. Все становится намного веселее, если мы начинаем складывать сигналы, которые меняются во времени, то есть переменные сигналы. Они могут быть как периодические, так и непериодические.
Рассмотрим самый простой пример. Есть два синусоидальных сигнала с одинаковыми амплитудами, частотами и фазами. Подадим их на сумматор. Что получится в итоге?
В момент времени t1 у нас амплитуда сигнала А была равна 1 В, амплитуда сигнала В тоже 1 В.
В сумме их результат в момент времени t1 будет равен 2 В, что мы и видим на сигнале A+B
Если сместить фазу одного из сигналов на 180 градусов, относительно другого, а амплитуды и частоты сигналов оставить без изменения, то чему будет равняться их сумма? Сместим второй сигнал на 180 градусов и суммируем их амплитуды в каждый момент времени. Сумма будет равняться нулю, что и видно на рисунке ниже.
Сложение двух сигналов в Proteus
Если надо сложить в теории два каких-нибудь два сложных сигнала с разными фазами, амплитудами, частотами, то проще всего прибегнуть к различным симуляторам.
Один из них – это Proteus. С помощью него можно сложить два любых сигнала и посмотреть их сумму.
Для этого надо выбрать синусоидальный генератор.
Затем виртуальный осциллограф.
Задать параметры генератору.
Теперь можно сложить два синусоидальных сигнала с одинаковыми амплитудами, фазами и частотами.
Прописать амплитуду и частоту каждого сигнала и нажать «пуск».
Нажать правой кнопкой мыши на виртуальный осциллограф и нажать Digital Oscilloscope.
Для того, чтобы найти их сумму, достаточно нажать на кнопку A+B.
Получаем сумму двух сигналов.
В таком виртуальном осциллографе можно складывать любые два сигнала.
Сумматор
Сумматор — устройство, преобразующее информационные сигналы (аналоговые или цифровые) в сигнал, эквивалентный сумме этих сигналов. [1]
Содержание
История
Классификация сумматоров
В зависимости от формы представления информации различают сумматоры аналоговые и цифровые. [1]
По способу реализации
По принципу действия
По архитектуре
По способу действия
По способу организации переноса
Двоичный сумматор
Двоичный сумматор может быть определён тремя способами:
1. табличным, в виде таблицы истинности,
2. аналитическим, в виде формулы (СДНФ),
3. графическим, в виде логической схемы.
Так как формулы и схемы могут преобразовываться, то, одной таблице истинности двоичного сумматора могут соответствовать множества различных формул и схем. Поэтому, табличный способ определения двоичного сумматора является основным.
| x0=A | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | ||
|---|---|---|---|---|---|---|---|---|---|---|
| x1=B | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | ||
| x2=Pi-1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | Название действия (функции) | Номер функции |
| Si | 1 | 0 | 0 | 1 | 0 | 1 | 1 | 0 | Бит суммы по модулю 2 | F3,150 |
| Pi | 1 | 1 | 1 | 0 | 1 | 0 | 0 | 0 | Бит переноса | F3,232 |
СДНФ суммы по модулю 2:
СДНФ бита переноса:
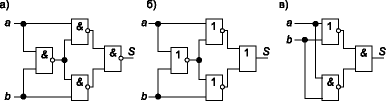
Cхема, которая обеспечивает сложение двух однобитных чисел А и В называется полусумматором. Полусумматор имеет 4 сигнальных линии: два входа для сигналов, представляющих одноразрядные двоичные числа А и В, и два выхода: сумма А и В по модулю 2 (S) и сигнал переноса (P). При этом S наименее значимый бит, а P наиболее значимый бит.
Схема полного сумматора может быть использована в качестве «строительных блоков» для построения схем многоразрядных сумматоров, путём добавления одноразрядных полных сумматоров. Для каждой цифры, которую схема должна быть в состоянии обрабатывать, используется один полный сумматор.
Двоичный одноразрядный полный сумматор является полной тринарной (трёхоперандной) двоичной логической функцией с бинарным (двухразрядным) выходом. Все три операнда и оба выходных разряда однобитные.
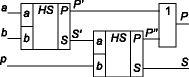
Может быть построен как тринарная (трёхоперандная) двоичная логическая функция с бинарным выходом [5] с временем выполнения операции сложения 2dt, но, для уменьшения аппаратных затрат, обычно строится трёхступенчатым, состоящим из трёх узлов: двух полусумматоров, которые являются полными бинарными (двухоперандными) двоичными логическими функциями с унарным выходом и логического элемента «2ИЛИ».
Троичный сумматор
Так как возможно несколько видов физической реализации троичных систем: трёхуровневая однопроводная, двухуровневая двухразрядная двухпроводная, двухуровневая трёхразрядная одноединичная трёхпроводная, двухуровневая трёхразрядная однонулевая и др., то возможны и несколько видов троичных сумматоров.
Троичный одноразрядный полный сумматор в троичной несимметричной системе счисления является неполной тринарной (трёхоперандной) троичной логической функцией. Два операнда — два слагаемых — полные, третий операнд — троичный разряд переноса — неполный и имеет только два значения 0 и 1 из трёх.
В несимметричной троичной системе счисления
| x0 | 2 | 1 | 0 | 2 | 1 | 0 | 2 | 1 | 0 | 2 | 1 | 0 | 2 | 1 | 0 | 2 | 1 | 0 | слагаемое |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| x1 | 2 | 2 | 2 | 1 | 1 | 1 | 0 | 0 | 0 | 2 | 2 | 2 | 1 | 1 | 1 | 0 | 0 | 0 | слагаемое |
| x2 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | Перенос из n-1 разряда |
| S | 2 | 1 | 0 | 1 | 0 | 2 | 0 | 2 | 1 | 1 | 0 | 2 | 0 | 2 | 1 | 2 | 1 | 0 | МЗР суммы, сумма по модулю 3 |
| C | 1 | 1 | 1 | 1 | 1 | 0 | 1 | 0 | 0 | 1 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | СЗР суммы, перенос в n+1 разряд |
В симметричной троичной системе счисления
| x0 | 1 | 0 | 7 | 1 | 0 | 7 | 1 | 0 | 7 | 1 | 0 | 7 | 1 | 0 | 7 | 1 | 0 | 7 | 1 | 0 | 7 | 1 | 0 | 7 | 1 | 0 | 7 | слагаемое | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| x1 | 1 | 1 | 1 | 0 | 0 | 0 | 7 | 7 | 7 | 1 | 1 | 1 | 0 | 0 | 0 | 7 | 7 | 7 | 1 | 1 | 1 | 0 | 0 | 0 | 7 | 7 | 7 | слагаемое | |
| x2 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 7 | 7 | 7 | 7 | 7 | 7 | 7 | 7 | 7 | Перенос из n-1 разряда | Номер функции |
| S | 0 | 7 | 1 | 7 | 1 | 0 | 1 | 0 | 7 | 7 | 1 | 0 | 1 | 0 | 7 | 0 | 7 | 1 | 1 | 0 | 7 | 0 | 7 | 1 | 7 | 1 | 0 | МЗР суммы | F3,-624603703776 |
| C | 1 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 7 | 0 | 0 | 0 | 0 | 0 | 7 | 0 | 7 | 7 | СЗР суммы (трит переноса в n+1 разряд) | F3,3483426737048 |
Троичный зеркально-симметричный одноразрядный полный сумматор описан в [10]
Принципиальная схема одноразрядного сумматора в несимметричной троичной системе счисления в трёхбитной одноединичной системе троичных логических элементов
Принципиальная схема троичного одноразрядного сумматора в двухбитной системе троичных логических элементов
Принципиальная схема троичного полного одноразрядного сумматора, работающего в троичной симметричной системе счисления Фибоначчи в трёхбитной одноединичной системе троичных логических элементов
Принципиальная схема троичного полного сумматора в троичной симметричной системе счисления Фибоначчи в двухбитной системе троичных логических элементов
См. также
Примечания
Литература
Ссылки
Полезное
Смотреть что такое «Сумматор» в других словарях:
Сумматор — в нейронных сетях блок, суммирующий сигналы, поступающие от нейронов через синапсы. В общем случае сумматор может преобразовывать сигналы и передавать их нейронам или сумматорам тоже через синапсы. См. также: Нейронные сети Финансовый словарь… … Финансовый словарь
сумматор — регистр, накопитель, тотализатор, суммирующее устройство; интегросумматор Словарь русских синонимов. сумматор сущ., кол во синонимов: 1 • интегросумматор (1) … Словарь синонимов
СУММАТОР — узел арифметического устройства ЭВМ, осуществляющий операцию суммирования чисел. Выполняется на логических элементах, интегральных схемах … Большой Энциклопедический словарь
СУММАТОР — (1) аналоговый устройство аналоговых вычислительных (см.) для преобразования информационных сигналов различных физ. процессов в суммы нескольких физ. величин. В зависимости от физ. природы входных и выходных величин суммирующие устройства делятся … Большая политехническая энциклопедия
сумматор — 3.1.28 сумматор: Элемент кабельной распределительной сети, обеспечивающий сложение энергии радиосигналов (оптических сигналов) на общей нагрузке. Источник … Словарь-справочник терминов нормативно-технической документации
СУММАТОР — а; м. Основной узел арифметического устройства цифровой вычислительной машины или отдельный прибор, выполняющий операцию сложения двух чисел. Стрелка сумматора. * * * СУММАТОР СУММАТОР, узел арифметического устройства ЭВМ, осуществляющий операцию … Энциклопедический словарь
сумматор — sudėtuvas statusas T sritis automatika atitikmenys: angl. adder; combining unit; summation instrument; summator; summer vok. Addiereinrichtung, f; Addierer, m; Addierwerk, n; Summator, m; Summierer, m; Summierungseinrichtung, f rus. сумматор, m;… … Automatikos terminų žodynas
Сумматор — (от позднелат. surnmo складываю, от лат. summa сумма, итог) основной узел арифметического устройства (См. Арифметическое устройство) ЦВМ, посредством которого осуществляется операция сложения чисел. При поразрядном сложении десятичных… … Большая советская энциклопедия
Сумматор — м. Один из элементов ЭВМ, выполняющий суммирование. Толковый словарь Ефремовой. Т. Ф. Ефремова. 2000 … Современный толковый словарь русского языка Ефремовой
Сумматоры: определения, классификация, уравнения, структуры и применение
Основной элементарной операцией, выполняемой над кодами чисел в цифровых устройствах, является арифметическое сложение.
Сумматор — логический операционный узел, выполняющий арифметическое сложение кодов двух чисел. При арифметическом сложении выполняются и другие дополнительные операции: учёт знаков чисел, выравнивание порядков слагаемых и тому подобное. Указанные операции выполняются в арифметическо-логических устройствах (АЛУ) или процессорных элементах, ядром которых являются сумматоры.
Сумматоры классифицируют по различным признакам.
Параллельный сумматор в простейшем случае представляет собой n одноразрядных сумматоров, последовательно (от младших разрядов к старшим) соединённых цепями переноса. Однако такая схема сумматора характеризуется сравнительно невысоким быстродействием, так как формирование сигналов суммы и переноса в каждом i-ом разряде производится лишь после того, как поступит сигнал переноса с (i-1)-го разряда.Таким образом, быстродействие сумматора определяется временем распространения сигнала по цепи переноса. Уменьшение этого времени — основная задача при построении параллельных сумматоров.
Для уменьшения времени распространения сигнала переноса применяют: конструктивные решения, когда используют в цепи переноса наиболее быстродействующие элементы; тщательно выполняют монтаж без длинных проводников и паразитных ёмкостных составляющих нагрузки и (наиболее часто) структурные методы ускорения прохождения сигнала переноса.
Сумматоры, которые имеют постоянное время, отводимое для суммирования, независимое от значений слагаемых, называют синхронными.
Последние две структуры строятся либо на счётных триггерах (сейчас практически не используются), либо по структуре “комбинационный сумматор – регистр хранения” (сейчас наиболее употребляемая схема).
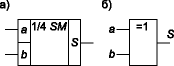
Простейшим двоичным суммирующим элементом является четвертьсумматор. Происхождение названия этого элемента следует из того, что он имеет в два раза меньше выходов и в два раза меньше строк в таблице истинности по сравнению с полным двоичным одноразрядным сумматором. Наиболее известны для данной схемы названия: элемент “сумма по модулю 2” и элемент “исключающее ИЛИ”. Схема (рис. 1) имеет два входа а и b для двух слагаемых и один выход S для суммы. Работу её отражает таблица истинности 1 (табл. 1), а соответствующее уравнение имеет вид