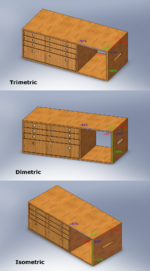
для чего применяются аксонометрические проекции

Аксонометрическая проекция

Аксонометрическая проекция (от др.-греч. ἄξων «ось» и др.-греч. μετρέω «измеряю») — способ изображения геометрических предметов на чертеже при помощи параллельных проекций.

Предмет с системой координат, к которой он отнесён, проецируют на произвольную плоскость (картинная плоскость аксонометрической проекции) таким образом, чтобы эта плоскость не совпадала с его координатной плоскостью. В этом случае получается две взаимосвязанные проекции одной фигуры на одну плоскость, что позволяет восстановить положение в пространстве, получив наглядное изображение предмета. Так как картинная плоскость не параллельна ни одной из координатных осей, то имеются искажения отрезков по длине параллельных координатным осям. Это искажение может быть равным по всем трём осям — изометрическая проекция, одинаковыми по двум осям — диметрическая проекция и с искажениями разными по всем трём осям — триметрическая проекция.

Содержание

Стандартизированные аксонометрические проекции [1]

См. также

Источники

Литература

Полезное

Смотреть что такое «Аксонометрическая проекция» в других словарях:

аксонометрическая проекция — 3.1 аксонометрическая проекция: Проекция на плоскость с помощью параллельных лучей, идущих из центра проецирования (который удален в бесконечность) через каждую точку объекта до пересечения с плоскостью, на которую проецируется объект. 3.2… … Словарь-справочник терминов нормативно-технической документации

Аксонометрическая проекция — способ изображения предметов на чертеже при помощи параллельных проекций в трех измерениях. (Архитектура: иллюстрированный справочник, 2005) … Архитектурный словарь

Проекция аксонометрическая — Аксонометрическая проекция: проекция на плоскость с помощью параллельных лучей, идущих из центра проецирования (который удален в бесконечность) через каждую точку объекта до пересечения с плоскостью, на которую проецируется объект. Источник:… … Официальная терминология

Проекция (геометрия) — У этого термина существуют и другие значения, см. Проекция. Проекции Параллельная Прямоугольная (ортогональная) Аксонометрическая Изометрическая Диметрическая Триметрическая Косоугольная Аксонометрическая Изометрическая Диметрическая… … Википедия

Проекция косоугольная — Косоугольная проекция: аксонометрическая проекция, у которой направление проецирования неперпендикулярно к плоскости проецирования. Источник: ГОСТ 2.317 2011. Межгосударственный стандарт. Единая система конструкторской документации.… … Официальная терминология

Проекция прямоугольная — Прямоугольная проекция: аксонометрическая проекция, у которой направление проецирования перпендикулярно к плоскости проецирования. Источник: ГОСТ 2.317 2011. Межгосударственный стандарт. Единая система конструкторской документации.… … Официальная терминология

Изометрическая проекция — Проекции Параллельная Прямоугольная (ортогональная) Аксонометрическая Изометрическая Диметрическая Триметрическая Косоугольная Аксонометрическая Изометрическая Диметрическая Триметрическая Перспективная (центральная) … Википедия

Косоугольная проекция — Проекции Параллельная Прямоугольная (ортогональная) Аксонометрическая Изометрическая Диметрическая Триметрическая Косоугольная Аксонометрическая Изометрическая Диметрическая Триметрическая Перспективная (центральная) Прочие Птичий глаз Рыбий глаз … Википедия

Диметрическая проекция — Проекции Параллельная Прямоугольная (ортогональная) Аксонометрическая Изометрическая Диметрическая Триметрическая Косоугольная Аксонометрическая Изометрическая Диметрическая Триметрическая Перспективная (центральная) … Википедия

Триметрическая проекция — Проекции Параллельная Прямоугольная (ортогональная) Аксонометрическая Изометрическая Диметрическая Триметрическая Косоугольная Аксонометрическая Изометрическая Диметрическая Триметрическая Перспективная (центральная) … Википедия

Источник

Аксонометрические проекции

Комплексный чертеж является графически простым и удобно из­меряемым. Но по нему не всегда легко представить предмет в простран­стве. Необходим чертеж, дающий и наглядное представление.

Он может быть получен при проецировании предмета вместе с осями координат на одну плоскость. В этом случае на одной проекции можно получить на­глядное и метрически определенное изображение. Такие виды изображе­ний называют аксонометрическими проекциями.

Слово «аксонометрия» (от гр. axon — ось и metreo — измеряю) пере­водится как «измерение по осям».

Способ аксонометрического проецирования состоит в том, что фи­гура вместе с осями прямоугольных координат (к которым она отнесена в пространстве) проецируется на некоторую плоскость. Эту плоскость называют плоскостью аксонометрических проекций, или картинной плоскостью.

При проецировании фигуры проецирующие лучи могут выходить из одной точки — центральная аксонометрия или быть параллельными друг другу — параллельная аксоносметрия. В дальнейшем мы будем рас­сматривать только параллельную аксонометрию.

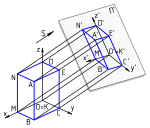
Построим аксонометрическую проекцию точки A, отнесенной к трем взаимно перпендикулярным плоскостям проекций (рис. 1).

Введем некоторые наименования:

Q — плоскость аксонометрических проекций (картинная плос­кость);

I — направление проецирования

α — угол наклона направления проецирования I к плоскости аксо­нометрических проекций Q (картинной плоскости).

Из точек о, а_х, а_у, а_z — проведем проецирующие лучи до пересечения с плоскостью Q и найдем аксонометрические проекции этих точек о₁, а_х1, а_y1, а_z1.

х_1, у₁, z₁ — аксонометрические оси координат (аксонометрические оси);

А₁ — аксонометрическая проекция точки А;

В зависимости от положения плоскостей проекций Н, V, W, плос­кости аксонометрических проекций Q и направления проецирования I координаты точки будут проецироваться с различными искажениями. Чтобы учесть эти факторы на осях координат отложим масштабные от­резки и построим их аксонометрические проекции.

При построении аксонометрии фигуры учитывают не длины мас­штабных отрезков, а отношение длины аксонометрической проекции масштабного отрезка к его действительной величине. Эти отношения на­зываются коэффициентом искажения по оси.

Обозначим эти коэффициенты:

В зависимости от направления проецирования по отношению к плоскости аксонометрических проекций Q аксонометрические проекции делятся на:

Доказано, что сумма квадратов коэффициентов искажения удовле­творяет уравнениям:

Основная теорема аксонометрии

Занимаясь теорией аксонометрии, немецкий геометр К. Польке в 1853 году предложил и доказал для частного случая теорему, названную основной теоремой аксонометрии: «Любые три отрезка, выходящие из одной точки на плоскости, могут быть приняты за параллельные проек­ции трех равных и взаимно перпендикулярных отрезков в пространстве».

Доказательство этой теоремы в общем виде было дано в 1864 г. другим немецким геометром Г. Шварцем. С этого времени основная теорема ак­сонометрии стала называться теоремой Польке — Шварца.

Из рассмотренного выше можно вывести определение аксономет­рии:

Аксонометрией называется изображение предмета на плоскости, отнесенное к определенной системе координат и выполненное в опреде­ленном масштабе с учетом коэффициентов искажения.

В зависимости от соотношения между коэффициентами искажения по осям различают следующие аксонометрические проекции:

Наименование проекций произошло от древнегреческих слов:

«isos» — одинаковый (изометрическая проекция — проекция с оди­наковыми коэффициентами искажения по всем трем осям);

«di» — двойной (диметрическая проекция — проекция с одинаковы­ми коэффициентами искажения по двум осям);

«treis» — три (триметрическая проекция — проекция с разными ко­эффициентами искажения по всем трем осям).

Источник

Понятие об аксонометрических проекциях

Наглядные изображения применяют для пояснения чертежей деталей и машин. По ним легче представить форму предмета, чем по чертежу в трёх видах.

Одним из видов наглядных изображений являются аксонометрические изображения.

Аксонометрия в переводе с греческого означает «измерение по осям».

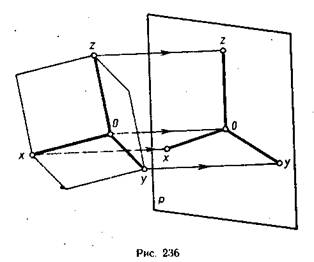
Аксонометрические проекции получают путём проецирования параллельными лучами

предмета, который связан с осями прямоугольных координат, на некоторую плоскость Р (рис. 103).

Таким образом, аксонометрическая проекция – это проекция только на одну плоскость.

Чтобы изображение получилось наглядным, проецирующие лучи не должны быть параллельны ни одной оси координат. Тогда на плоскости Р будут, хоть и с искажениями, изображены все три измерения предмета.

Аксонометрические проекции в зависимости от направления проецирования делятся на два вида: прямоугольные, когда направление проецирования перпендикулярно плоскости Р (угол φ=90°), и косоугольные, когда угол φ≠90°.

Если плоскость Р не параллельна ни одной из координатных плоскостей x,y,z, то на аксонометрической проекции у предмета искажаются все три его измерения. Если же плоскость Р параллельна одной или двум осям координат, то у предмета искажаются размеры соответственно по двум его измерениям или по одному.

Величина искажения определяется коэффициентом искажения, который равен отношению длины аксонометрической проекции отрезка, параллельного соответствующей оси координат, к его действительной длине. Любая аксонометрическая проекция имеет три коэффициента искажения по числу осей координат.

В зависимости от того, разные они или одинаковые, аксонометрические проекции делят на изометрические (коэффициенты искажения равны по всем трём осям) и триметрические (коэффициенты искажения по всем осям разные).

Стандартные виды аксонометрии. Изометрия. Диметрия

Наиболее распространёнными видами аксонометрических проекций являются прямоугольная изометрическая проекция (изометрия) и прямоугольная диметрическая проекция (диметрия), основные правила построения которых определены стандартом.

Прямоугольная изометрия представляет собой аксонометрическую проекцию с направлением проецирования, перпендикулярным к плоскости аксонометрических проекций одинаковыми по всем трём осям коэффициентами искажения, равными 0,82.

Оси изометрии (рис. 104а) составляют между собой углы 120°. Ось Z расположена вертикально. Для упрощения построения коэффициент искажения принимают равным 1.

Изображение при этом получается увеличенным, но вид его не меняется, т.к. сохраняется пропорциональность всех его размеров.

На рис. 104б и в приведены два способа построения осей в изометрии.

Прямоугольная диметрия представляет собой аксонометрическую проекцию с направлением проецирования, перпендикулярным аксонометрической плоскости проекций Р и одинаковыми коэффициентами искажения по осям х и z.

Ось х (рис. 105а) составляет с горизонтальной прямой угол 7°10′, а ось у – угол 41°25′.

Ось z занимает вертикальное положение. На рис. 105б показан графический способ построения осей диметрии.

В диметрии коэффициенты искажения по осям х и z равны 0,94, а по оси у – 0,47. При построениях первый коэффициент округляют до 1, а второй – до 0,5. Таким образом, отрезки, параллельные осям координат х и z, откладывают в натуральную величину, а длину отрезков, параллельных оси у, уменьшают в два раза.

Построение окружности в аксонометрии

Изометрия. Изометрические проекции окружностей, расположенных в плоскостях проекций или в плоскостях, им параллельных, есть эллипсы (рис. 106).

Большие оси этих эллипсов равны l,22Dокр, а малые 0,71Dокр, где Dокр – диаметр изображаемой окружности. Большая ось эллипсов всегда перпендикулярна к той аксонометрической оси, которая отсутствует в плоскости окружности, а малая совпадает с этой осью или параллельна ей.

Практически при построении изометрии окружности эллипс обычно заменяют близким к нему по форме овалом, т.к. построение овала значительно проще.

Наиболее простой способ построения овала показан на рис. 107.

На рис. 108а,б построены изометрии окружностей, расположенных во фронтальной и профильной плоскостях.

Окружности, расположенные во фронтальной плоскости, проецируются в виде эллипсов с большой осью, равной 1,06Dокр, а малой – 0,94Dокр. Большие оси эллипсов, как и в изометрии, перпендикулярны к той аксонометрической оси, которая отсутствует в данной плоскости, а малые оси совпадают с направлением этой оси.

Диметрии окружностей (эллипсы) обычно заменяют овалами, размеры осей которых равны размерам соответствующих осей эллипсов. Построение этих овалов показано на рис. 110. На рис. 110а построения понятны по чертежу.

На рис. 110б строим оси диметрии х_р, у_р, z_р. Затем строим прямую, перпендикулярную оси у_р. Отложив на осях х_р и z_р радиус заданной окружности, получим точки М, К, N, L, которые являются точками сопряжения дуг овала. Через точки М и N проводим горизонтальные прямые. В пересечении этих прямых с осью у_р и перпендикуляром к ней получим точки О₁, О₂, О₃, О₄. Из центров O₁ и О₃ опишем дуги радиусом R₁=О₃ K, а из центров О₂ и О₄ – дуги радиусом R₂=О₂M.

Аксонометрические изображения предметов

Приступая к построению аксонометрической проекции предмета, следует выбрать вид аксонометрии, обеспечивающий наибольшую наглядность изображения. Затем предмет связывают с системой прямоугольных координат, оси которой обычно совмещают с осями симметрии предмета. Только после этого можно приступить к построению аксонометрии.

Построение аксонометрии предмета обычно начинают с построения аксонометрии одной из его проекций (вторичной проекции). Затем полученное изображение дополняют построением третьего измерения всех его точек.

На рис. 111 показан пример построения прямоугольной изометрии предмета через построение его горизонтальной проекции.

На рис. 112 приведен пример построения прямоугольной изометрии детали путём построения её вторичной фронтальной проекции.

Для выявления внутренней формы предмета, изображённого в аксонометрии, в некоторых случаях применяют разрезы, которые условно называют вырезами. При этом используют две секущие плоскости, обычно совпадающие с плоскостями симметрии предмета (рис. 113).

рис. 111 рис. 112 рис. 113

Линии штриховки сечений в аксонометрических проекциях наносят параллельно одной из диагоналей проекций квадратов, лежащих в соответствующих координатных плоскостях. Стороны квадратов параллельны аксонометрическим осям (рис. 114).

Источник

АКСОНОМЕТРИЧЕСКИЕ ПРОЕКЦИИ

Аксонометрические проекции применяются для наглядного изображения различных предметов. Предмет здесь изобра­жают так, как его видят (под определенным углом зрения). На таком изображении отраже­ны все три пространственных измерения, по­этому чтение аксонометрического чертежа обычно не вызывает затруднений.

Аксонометрический чертеж можно получить как с помощью прямоугольного проецирова­ния, так и с помощью косоугольного проеци­рования. Предмет располагают так, чтобы три основных направления его измерений (высота, ширина, длина) совпадали с осями координат и вместе с ними спроецировались бы на плос­кость. Направление проецирования не должно совпадать с направлением осей координат, т. е. ни одна из осей не будет проецироваться в точ­ку. Только в этом случае получится наглядное изображение всех трех осей.

Для получения прямоугольных аксонометри­ческих проекций оси координат наклоняют от­носительно плоскости проекций Р_А так, чтобы их направление не совпадало с направлением проецирующих лучей. При косоугольном прое­цировании можно варьировать как направле­нием проецирования, так и наклоном коорди­натных осей относительно плоскости проекций. При этом координатные оси в зависимости от их угла наклона к аксонометрической плоско­сти проекций и направления проецирования будут проецироваться с разными коэффициен­тами искажения. В зависимости от этого будут получаться разные аксонометрические проек­ции, отличающиеся расположением осей коор­динат. ГОСТ 2.317—69 (СТ СЭВ 1979—79) предусматривает следующие аксонометричес­кие проекции: прямоугольная изометрическая проекция; прямоугольная диметрическая про­екция; косоугольная фронтальная изометриче­ская проекция; косоугольная горизонтальная изометрическая проекция; косоугольная фрон­тальная диметрическая проекция.

§26. ПРЯМОУГОЛЬНЫЕ АКСОНОМЕТРИ­ЧЕСКИЕ ПРОЕКЦИИ

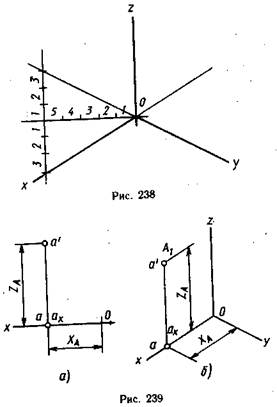
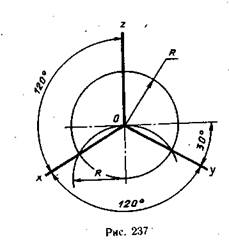
Изометрическая проекция отлича­ется большой наглядностью и широко приме­няется в практике. Координатные оси при по­лучении изометрической проекции наклоняют относительно аксонометрической плоскости проекций так, чтобы они имели одинаковый угол наклона (рис. 236). В этом случае они проецируются с одинаковым коэффициентом искажения (0,82) и под одинаковым углом друг к другу (120°).

В практике коэффициент искажения по осям обычно принимают равным единице, т. е. от­кладывают действительную величину размера. Изображение получается увеличенным в 1,22 раза, но это не приводит к искажениям формы и не сказывается на наглядности, а упрощает построения.

Аксонометрические оси в изометрии прово­дят, предварительно построив углы между ося­ми х, у и z (120°) или углы наклона осей х и у к горизонтальной прямой (30°). Построение осей в изометрии помощью циркуля показано на рис. 237, где радиус R взят произвольно. На рис. 238 показан способ построения осей х и у с использованием тангенса угла 30°. От точки О — точки пересечения аксонометриче­ских осей откладывают влево или вправо по горизонтальной прямой пять одинаковых отрез­ков произвольной длины и, проведя через последнее деление вертикальную прямую, откла­дывают на ней вверх и вниз по три таких же отрезка. Построенные точки соединяют с точ­кой О и получают оси Ох и Оу.

с

Откладывать (строить) размеры и произво­дить измерения в аксонометрии можно только по осям Ох, Оу и Оz или на прямых, парал­лельных этим осям.

На рис. 239 показано построение точки А в изометрии по ортогональному чертежу (рис. 239, а). Точка А расположена в плоско­сти V. Для построения достаточно построить вторичную проекцию а‘ точки А (рис. 239, б) на плоскости xOz по координатам Х_А и Z_A. Изображение точки А совпадает с ее вторичной проекцией. Вторичными проекциями точки называют изображения ее ортогональ­ных проекций в аксонометрии.

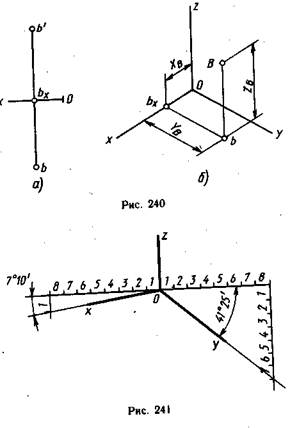
На рис. 240 показано построение точки В в изометрии. Сначала строят вторичную проек­цию точки В на плоскости хОу. Для этого от начала координат по оси Ох откладывают коор­динату Х_в (рис. 240, б), получают вторичную проекцию точки b_х. Из этой точки параллельно оси Оу проводят прямую и на ней откладывают координату Y_B.

Построенная точка b на аксо­нометрической плоскости будет вторичной про­екцией точки В. Проведя из точки b прямую, параллельную оси Oz, откладывают координа­ту Z_B и получают точку В, т. е. аксонометри­ческое изображение точки В. Аксонометрию точки В можно построить и от вторичных про­екций на плоскости zОх или zОу.

Прямоугольная диметрическая проекция. Координатные оси располагают так, чтобы две оси Ох и Оz имели одинаковый угол наклона ипроецировались с одинаковым коэффициентом искажения (0,94), а третья ось Оу была бы наклонена так, чтобы коэффициент искажения при проецировании был в два раза меньше (0,47). Обычно коэффициент искажения по осям Ох и Oz принимают рав­ным единице, а по оси Оу — 0,5. Изображение получается увеличенным в 1,06 раза, но это так же, как и в изометрии, не сказывается на наглядности изображения, а упрощает постро­ение. Расположение осей в прямоугольной диметрии показано на рис. 241. Строят их, от­кладывая углы 7° 10′ и 41°25′ от горизонталь­ной линии по транспортиру, или откладывая одинаковые отрезки произвольной длины, как показано на рис. 241. Полученные точки сое­динить с точкой О. При построении прямо­угольной диметрии необходимо помнить, что действительные размеры откладывают только на осях Ох и Oz или на параллельных им линиях. Размеры по оси Оу и параллельно ей откладывают с коэффициентом искажения 0,5.

§27. КОСОУГОЛЬНЫЕ АКСОНОМЕТРИ­ЧЕСКИЕ ПРОЕКЦИИ

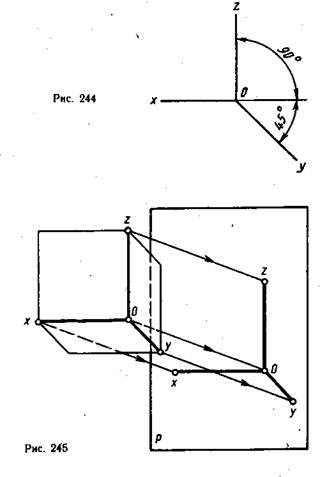
Фронтальная изометрическая проекция. Расположение аксонометриче­ских осей показано на рис. 242. Угол наклона оси Оу к горизонтали обычно равен 45°, но может иметь значение 30 или 60°.

Горизонтальная изометрическая проекция. Расположение аксонометричес­ких осей показано на рис. 243. Угол наклона оси Оу к горизонтали обычно равен 30°, но может иметь значение 45 или 60°. При этом угол 90° между осями Ох и Оу должен сохра­няться.

Фронтальную и горизонтальную косоуголь­ные изометрические проекции строят без иска­жения по осям Ох, Оу и Oz.

Фронтальная диметрическая про­екция. Расположение осей показано на рис. 244. Рис. 245 иллюстрирует проецирова­ние осей координат на аксонометрическую плоскость проекций. Плоскость xOz параллель­на плоскости Р. Допускается ось Оу прово­дить под углом 30 или 60° к горизонтали, коэффициент искажения по оси Ох и Oz при­нят равным 1, а по оси Оу — 0,5.

§28. ПОСТРОЕНИЕ ПЛОСКИХ ГЕОМЕТ­РИЧЕСКИХ ФИГУР В АКСОНОМЕТРИИ

Основанием ряда геометрических тел явля­ется плоская геометрическая фигура: много­угольник или окружность. Чтобы построить геометрическое тело в аксонометрии, надо уметь строить прежде всего его основание, т. е. плоскую геометрическую фигуру. Для примера рассмотрим построение плоских фигур в пря­моугольной изометрической и диметрической проекции. Построение многоугольников в аксо­нометрии можно выполнять методом коорди­нат, когда каждую вершину многоугольника строят в аксонометрии как отдельную точку (построение точки методом координат рассмотрено в § 26), затем построенные точки соеди­няют отрезками прямых линий и получают ло­маную замкнутую линию в виде многоугольни­ка. Эту задачу можно решить иначе. В пра­вильном многоугольнике построение начинают с оси симметрии, а в неправильном много­угольнике проводят дополнительную прямую, которая называется базой, параллельно одной из осей координат на ортогональном чертеже.

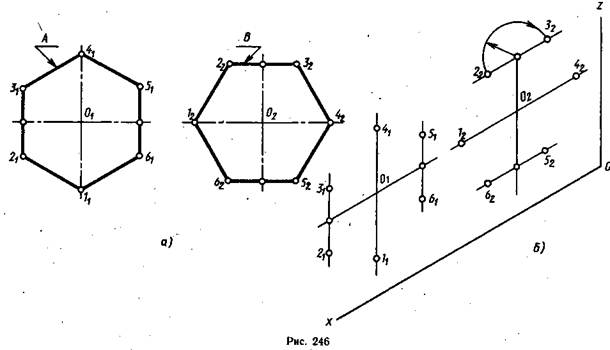Построение правильного шестиугольника в изометрической проекцииначинается с опреде­ления положения осей симметрии фигуры отно­сительно осей координат той плоскости проек­ций, в которой лежит шестиугольник. Предпо­ложим, что два шестиугольника А и В (рис. 246) на ортогональном чертеже находят­ся в плоскости V и их оси симметрии распола­гаются параллельно осям Oz и Ох. В аксоно­метрии в плоскости xOz проводят оси симмет­рии шестиугольников параллельно осям Oz и Ох. Центры шестиугольников располагают произвольно, так как рассматривается построе­ние вершин относительно осей симметрии. На ортогональном чертеже шестиугольника А на оси симметрии, параллельной Oz, лежат вер­шины 1 и 4 а на чертеже шестиугольника В на этой же оси расположены середины сторон 2 3 и 5 6. Расстояния между вершинами 1 и 4 и се­рединами сторон 2 3 и 5 6 измеряют от точек О₁ и О₂ на эпюре. Эти расстояния в изометрии откладывают от точек О₁ и О₂ (рис. 246,6).

На второй оси симметрии шестиугольника А, расположенной параллельно оси Ох, лежат середины сторон 2 3 и 5 6_У а шестиугольника В — вершины 1 и 4. Расстояния между верши­нами и серединами сторон измеряют на орто­гональном чертеже и соответственно переносят в изометрию.

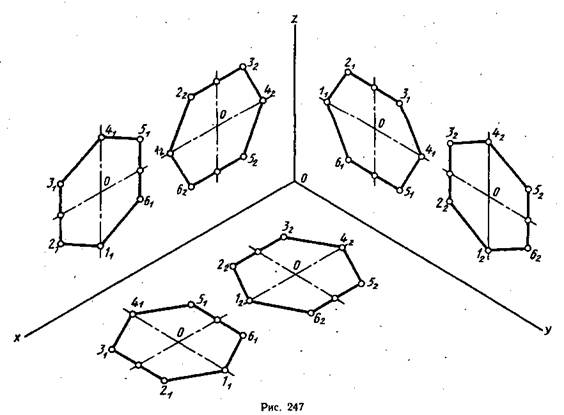
Далее через середины сторон в изометрии проводят прямые линии параллель­но направлению оси Oz для шестиугольника А и параллельно направлению оси Ох для ше­стиугольника В. На этих прямых откладывают отрезки, которые равны стороне шестиуголь­ника, и получают точки (вершины) 2₁, 3₁, 5₁, 6₁, 2₂, 3₂, 5₂, 6₂,. Для этого на ортогональном чертеже измеряют расстояние от середины сто­рон до ближайшей вершины и переносят в аксонометрию, где откладывают от соответст­вующих точек в обе стороны. Построенные точки последовательно соединяют отрезками прямых линий и получают изображения шести­угольников в аксонометрии. На рис. 247 по­строены шестиугольники в плоскостях V, Н и W.

В плоскости Н оси симметрии располагают­ся параллельно оси Ох н Оу, а в плоскости W — параллельно осям Oz и Оу₁.

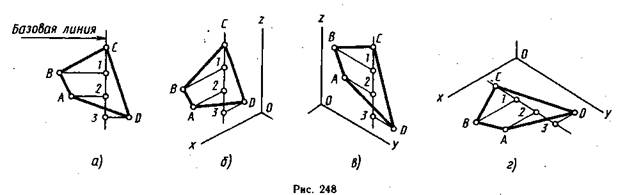
Построение неправильного многоугольника в изометрической проекции начинают с выбора базовой линии, лежащей в плоскости много­угольника и параллельной одной из осей коор­динат. Этой прямой могут быть сторона мно­гоугольника, диагональ или прямая, проведен­ная через вершину любого угла в плоскости многоугольника параллельно одной из осей координат плоскости, в которой лежит фигура.

Так, на рис. 248, а ортогонального чертежа через вершину С проведена базовая прямая, которая для плоскостей xOz и zOy (рис. 248, б и в) располагается параллельно направ­лению оси Oz, а для плоскости хОу (рис. 248, г) — оси Оу.

На этом же ортогональном чертеже через вершины остальных углов многоугольника пер­пендикулярно к этой прямой проведены линии до пересечения в точках 1, 2 и 3. Начинают построение заданной фигуры в аксонометрии с проведения прямой СЗ в каждой плоскости параллельно направлению той оси, которая выбрана по условию. На прямой СЗ произ­вольно выбирается точка, которая будет вер­шиной С. От точки С откладывают расстояния до точек 1, 2 и З измеренные на ортогональ­ном чертеже, и через эти точки проводят пря­мые параллельно направлению второй оси пло­скости. Строят вершины А, В и D многоуголь­ника. Для этого на ортогональном чертеже измеряют расстояния от точек 1, 2 и 3 до вер­шин А, В и D и откладывают их в аксономет­рии. Полученные точки последовательно сое­диняют отрезками прямых, получают заданный многоугольник в аксонометрии.

Построение многоугольника в прямоуголь­ной диметрической проекциивыполняют так же, как в прямоугольной изометрической про­екции, но отрезки, параллельные оси Оу в диметрии, уменьшают в два раза, учитывая коэф­фициент искажения по оси Оу.

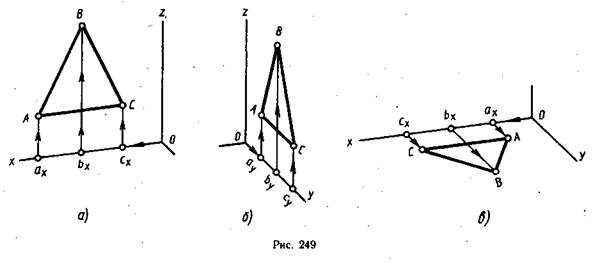
Рассмотрим построение треугольника ABC в прямоугольной диметрии по координатам его вершин.

Треугольник, расположенный в плоскости V, с координатами вершин Х_А = 45, Y_A = 0, Z_A = 15, Х_В = 30, Y_B = 0, Z_B = 45, Х_с = 15, Y_c = 0, Z_c = 15 построен на рис. 249, а. Его построение начинают с нахождения вторичных осевых проекций вершин. Для этого от точки О по оси Ох откладывают координаты Х_А Х_в, Х_с вершин треугольника и получают точки а_х> Ь_ХУ с_х. От них на прямых, параллельных оси Oz, откладывают координаты Z_A Z_В Z_С и получают аксонометрические изображения вер­шин треугольника. Затем вершины соединяют.

Построение треугольников с координатами вершин Х_А = 0, Y_A= 15, Z_A = 15, Х_В = 0, Y_B = 30, Z_B = 45, Х_с = 0, Y_c = 45, Z_c = 15, лежащих в плоскости W (рис. 249, б) и в плоскости Н (рис. 249, в), аналогично. При этом по оси Оу и в том, и. в другом случае откладывают половину координаты Y, учиты­вая коэффициент искажения. Форма треуголь­ника в этих плоскостях искажается.

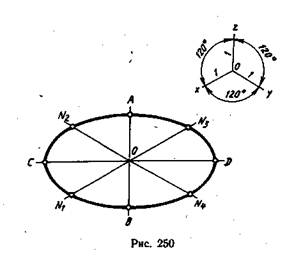
Изображение окружности в прямоугольной изометрической проекции во всех трех плоско­стях проекций представляет собой одинаковые по форме эллипсы.

Направление малой оси эллипса совпадает с направлением аксонометрической оси, перпен­дикулярной той плоскости проекций, в которой лежит изображаемая окружность. Так, если изображаемая окружность лежит в плоскости Н или в плоскости, параллельной Н. направление малой оси будет совпадать с на­правлением оси Oz (рис. 250). Если окруж­ность расположена в плоскости V или в плос­кости, параллельной ей, направление малой оси будет совпадать с направлением оси Оу.

Если окружность расположена в плоскости W или в плоскости, параллельной ей, направле­ние малой оси будет совпадать с осью Ох.

Большую ось эллипса проводят перпенди­кулярно малой оси. Величина малой оси эллип­са берется равной 0,71d, а величина большой оси—1,22d, где d — диаметр изображаемой окружности.

При построении эллипса, изображающего окружность небольшого диаметра, достаточно построить восемь точек, принадлежащих эл­липсу (рис. 250). Четыре из них являются концами осей эллипса (А, В, С, D), а четыре других (N₁, N₂, N₃, N₄) расположены на прямых, параллельных аксонометрическим осям, на расстоянии, равном радиусу изображаемой окружности от центра эллипса.

Замена эллипса овалом в прямоугольной изометрической проекции применяется для того, чтобы упростить построение.

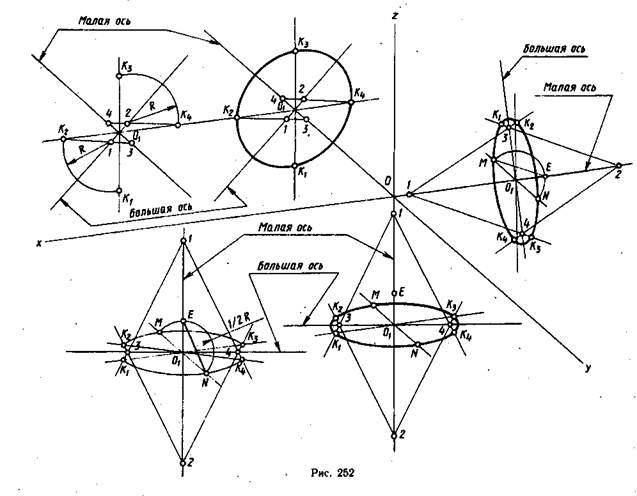
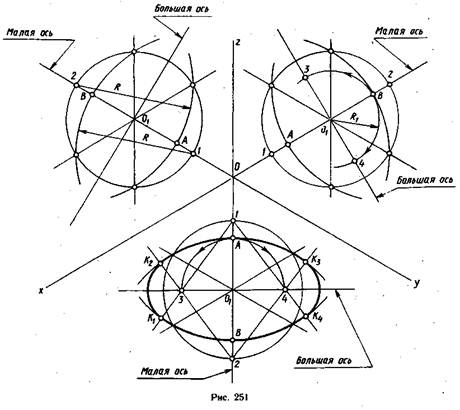
Овал состоит из четырех сопрягающихся дуг: двух больших и двух малых. Для его построе­ния необходимо определить четыре точки, че­рез которые проходят большие дуги, и четыре центра дуг. На рис. 251 показаны три случая расположения овала относительно аксономет­рических осей. В плоскости хОу построение доведено до конца, в двух других плоскостях построение остановлено на определенном этапе.

Построение овала начинают с проведения через центр овала (точка О) прямых, парал­лельных осям Ох и Oz для плоскости xOz; Oz и Оу для плоскости zOy; Ох и Оу для плос­кости хОу. Затем проводят малую и большую оси овала. Расположение осей овала относи­тельно аксонометрических осей и взаимное рас­положение большой и малой осей остаются такими же, как у эллипса, а размеры осей определяют построениями.

Из центра О₁ описывают окружность радиу­сом, равным радиусу изображаемой окружно­сти. В пересечении окружности с проведенными параллельно аксонометрическим осям прямы­ми получают четыре точки, через которые пройдут большие дуги, а на прямой, на кото­рой находится малая ось овала, получают точ­ки/и 2, которые являются центрами боль­ших дуг.

Радиус большой дуги R равен расстоянию от точки 1 или 2 до точек, в которых проведенная окружность пересекла прямые, параллельные аксонометрическим осям (рис. 251, плоскость xOz).

Дальнейшее построение овала (проведение малых дуг) показано на рис. 251 в плоскости zOy. Проведя большие дуги, построили малую ось овала АВ. Из центра О₁ радиусом, равным половине отрезка АВ, проводят дуги до пересе­чения с большой осью овала, получают точки 3 и 4. Эти точки будут центрами малых дуг овала.

Нахождение точек сопряжения больших и малых дуг показано на рис. 251 в плоскости хОу. Точки сопряжения находятся на прямых, проведенных через центры больших и малых дуг 1 3, 1 4, 2 3 и 2 4 в пересечении их с большими дугами. Найдя точки сопряжения К₁ К₂, К₃ и К₄, обводят сначала большие, а затем малые дуги овала.

Замена эллипса овалом в прямоугольной диметрической проекции. В прямоугольной диметрии так же, как и в изометрии, малая ось эллипса параллельна той аксонометрической оси, которая перпендикулярна плоскости про­екций, где расположена изображаемая окруж­ность. В плоскости хОz малая ось располага­ется в направлении оси Оу, в плоскости хОу — в направлении оси Ог, в плоскости zOy — в направлении оси Ох. Большую ось эллипса проводят перпендикулярно малой оси. Постро­ение начинают с центра овала (точки O₁). Затем через точку 0« проводят малую и боль­шую оси и прямые, параллельные аксономет­рическим осям, которые определяют данную плоскость. В плоскости xOz эти прямые про­водят параллельно осям Оz и Ох, в плоскости хОу — осям Ох и Оу, в плоскости zOy — осям Ог и Оу.

Рассмотрим построение овала в плоскости xOz (рис. 252). Из точки 0\ на прямых, парал­лельных осям Оz и Ox, откладывают отрезки, равные радиусу заданной окружности, полу­чают точки К₁ К₂, К₃ и К₄, которые будут точками касания дуг овала. Затем строят цент­ры 1 и 2 малых дуг. Для этого от точки О₁ в обе стороны по большой оси откладывают от­резки, равные 0,1D, где D — диаметр задан­ной окружности. Из центра 1 проводят дугу от точки К₁ до точки K₂, а из центра 2 — от точки K₃ до точки К₄. Известно, что точки касания лежат на прямых, соединяющих центры дуг. Значит, если точку касания K₂ соединить пря­мой линией с центром 1 и продолжить эту пря­мую до пересечения ее с малой осью, то полу­чим центр большой дуги (точка 3).

Второй центр (точка 4) лежит на прямой, проведенной через точки К₄ и 2 (рис. 252).

Из центров 3 и 4 проводят большие дуги овала от точки К₂ до точки Кз и от точки К₁ до точки К₄. Затем овал обводят циркулем с мягким грифелем. На рис. 252 на плоскости xOz показано слева построение центров 1, 2, 3 и 4, а справа — построенный и обведенный овал.

В плоскости zOy построение овала выполня­ют так же, как и в плоскости хОу. Направле­ние малой оси в этой плоскости перпендику­лярно оси Ох.

Косоугольные аксонометрические проекции рекомендуется применять в тех случаях, когда окружности на изображаемых деталях распо­ложены так, что все они находятся в положении, параллельном какой-либо плоскости про­екций. Тогда детали располагают так, чтобы окружности изображались в аксонометриче­ской плоскости без искажения, т. е. как окруж­ности. В косоугольных аксонометрических про­екциях изображают также детали, имеющие такое взаимное расположение граней, что при изображении в прямоугольных аксонометриче­ских проекциях они сильно искажаются. В этих случаях подбирают такую косоугольную проекцию, которая дает изображение детали без искажения.,

Источник