доказать что 1589 в квадрате 1 составное число

Доказать что 1589 в квадрате 1 составное число

Составные числа

Число так называемых простых чисел, т. е. целых чисел, больших единицы, не делящихся без остатка ни на какие другие целые числа, кроме единицы и самих себя, бесконечно велико.

Для удобства будем пользоваться условным символом n!, который обозначает произведение всех чисел от 1 до n включительно. Например 5! = 1 × 2 × 3 × 4 × 5. Мы сейчас докажем, что ряд

включительно состоит из n последовательных составных чисел.

состоит из двух слагаемых, каждое из которых кратно 3. Значит, и это число составное.

делится без остатка на 4, так как состоит из слагаемых, кратных 4.

Подобным же образом устанавливаем, что следующее число

кратно 5 и т. д. Иначе говоря, каждое число нашего ряда содержит множитель, отличный от единицы и его самого; оно является, следовательно, составным.

Если вы желаете написать, например, пять последовательных составных чисел, вам достаточно в приведенный выше ряд подставить вместо n число 5. Вы получите ряд

Или еще меньшие числа:

Попробуем теперь решить задачу:

Написать десять последовательных составных чисел.

На основании ранее сказанного устанавливаем, что в качестве первого из искомых десяти чисел можно взять

Искомой серией чисел, следовательно, может служить такая!

Однако существуют серии из десяти гораздо меньших последовательных составных чисел. Так, можно указать на серию даже не из десяти, а из тринадцати составных последовательных чисел уже во второй сотне:

Источник

Простые числа. Составные числа

Определение 1. Простое число − это натуральное число больше единицы, которое делится только на себя и на 1.

Другими словами число является простым, если имеет только два различных натуральных делителя.

Определение 2. Любое натуральное число, которое кроме самого себя и единицы имеет и других делителей, называется составным числом.

Другими словами натуральные числа, не являющиеся простыми числами, называются составными. Из определения 1 следует, что составное число имеет больше двух натуральных делителей. Число 1 не является ни простым, ни составным т.к. имеет только один делитель 1 и, кроме этого многие теоремы относительно простых чисел не имеют места для единицы.

Из определений 1 и 2 следует, что каждое целое положительное число больше 1 является либо простым, либо составным числом.

Ниже представлена программа для отображения простых чисел до 5000. Заполните ячейки, нажмите на кнопку «Создать» и подождите несколько секунд.

Таблица простых чисел

Теорема 1. Любое составное число всегда может быть представлено и притом единственным способом в виде произведения конечного числа простых чисел.

Если k₁ число простое, то k уже представлен в виде произведения простых чисел, в противном случае существует такое простое число p₂, что

Если k₂ число составное, то мы продолжаем процедуру до тех пор, пока k не будет представлено в виде произведения простых чисел:

Первая часть теоремы доказана. Покажем, далее, что разложение составного числа на простые множители единственно (естественно, порядок множителей в произведении может быть другим).

Допустим существует два разложения числа k:

Так как k=p₁p₂p₃. делится на простое число q₁, то по крайней мере один из множителей, например p₁ делится на q₁. Но p₁ простое число и делится только на 1 и на себя. Следовательно p₁=q₁ (т.к. q₁≠1)

Таким образом убеждаемся, что всякое простое число входящее множителем в первое разложение один или несколько раз, входит и во второе разложение минимум столько же раз и наоборот, всякое простое число, которое входит множителем во второе разложение один или несколько раз входит и в первое разложение минимум столько же раз. Следовательно любое простое число входит множителем в оба разложения одинаковое число раз и, таким образом, эти два разложения одинаковы.■

Разложение составного числа k можно записать в следующем виде

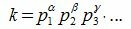(3)

Разложение (3) называется каноническим разложением числа.

Теорема 2. Количество простых чисел бесконечно много.

Доказательство. Предположим, что существует конечное число простых чисел, и пусть наибольшее простое число равно p. Рассмотрим все числа больше p. По предположению утверждения эти числа должны быть составными и должны делится по крайней мере на один из простых чисел. Выберем число, являющиеся произведением всех этих простых чисел плюс 1:

Число z больше p так как 2p уже больше p. p не делится ни на одно из этих простых чисел, т.к. при делении на каждое из них дает остаток 1. Таким образом мы приходим к противоречию. Следовательно существует бесчисленное множество простых чисел.

Данная теорема является частным случаем более общей теоремы:

Теорема 3. Пусть задана арифметическая прогрессия

где d разность арифметической прогрессии, m первый член, и пусть d и m взаимно простые числа. Тогда арифметическая прогрессия (5) содержит бесконечное множество простых чисел.

Нетрудно заметить, что при m=1 и d=1 мы получим теорему 2.

Число и сумма всех делителей числа

Теорема 1 дает возможность определить, делится число m на n, если эти числа разложены на простые множители.

Если m делится на n, то n является кратным m:

Тогда любое простое число, входящее в n, должно входить и в m, поэтому в n не могут входить другие простые множители, которые не входят в m и притом эти простые множители в n входят не более число раз, чем в m.

Справедливо и обратное. Если каждый простой множитель числа n входит по крайней мере столько же раз в число m, то m делится на n.

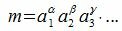Тогда все делители n числа m можно представить формулой

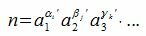(6)

Каждая из чисел n вычисленная формулой (6) является делителем числа m.

Очевидно, при разных значениях i, j, k имеем разные делители числа m. Тогда число всех делителей m равно:

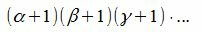Мы доказали следующую теорему:

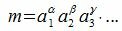каноническое разложение числа m. Тогда число делителей числа m равно:

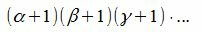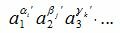
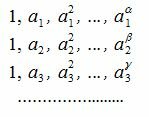Составим все произведения вида , которые различны между собой и являются множеством всех делителей числа m. Найдем сумму этих делителей. Для этого запишем ряды чисел

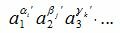
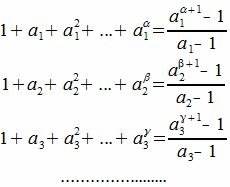Тогда для произведения вида берем по одному множителю из каждого горизонтального ряда. Используя правила умножения многочленов получим:

Заметим, что правая часть каждой строки является суммой членов геометрической прогрессии.

Следовательно сумма всех делителей числа m равна

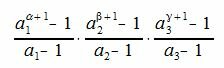(7)

Мы доказали следующую теорему:

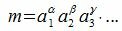каноническое разложение числа m. Тогда сумма всех делителей числа m равна выражению (7).

Источник

№ 636. ГДЗ Математика 5 класс Никольский. Помогите доказать, что число является составным.

Используя признаки делимости, докажите, что число:
а) 7690; 6)7395; в) 4256; г) 12 375; д) 12 321
является составным.

а) 7690 = 2 ∙ 3845 — составное
б) 7395 = 5 ∙ 1479 — составное
в) 4256 = 2 ∙2128 — составное
г) 12375 = 2475 ∙ 5 — составное
д) 12321 =3 ∙4107 — составное

Вычислите объём прямоугольного параллелепипеда, если его рёбра равны:
а) 18 см, 16 см, 5 см; б) 12 см, 45 см, 2 ( Подробнее. )

Самолёт поднялся в воздух в 14 ч 45 мин и приземлился в 17 ч 10 мин. Сколько времени он находился в полёте?

1. Через середину М сторони АВ трикутника АВС проведено площину, яка паралельна, прямій АС і перетинає сторону ВС у точці N. Довести NM ( Подробнее. )

Привет…Не могу справиться с ответом на такой вопрос…может кто поможет, а?
Чтобы пройти в следующий круг соревнований, футбольной ( Подробнее. )

Привет пользователи! Окажите пожалуйста услугу…ответить помогите….
В Волшебной стране бывает два типа погоды: хорошая и отличная, ( Подробнее. )

Источник

math4school.ru

Простые и составные числа

Немного теории

Простое число – это натуральное число, имеющее ровно два различных натуральных делителя: единицу и само себя. Все остальные натуральные числа, кроме единицы, называются составными. Таким образом, все натуральные числа больше единицы разбиваются на простые и составные. Изучением свойств простых чисел занимается теория чисел.

Приведём некоторые свойства простых чисел.

Основная теорема арифметики. Каждое натуральное число, большее единицы, представимо в виде произведения простых чисел, причём единственным способом с точностью до порядка следования сомножителей.

Простых чисел бесконечно много.

Если p – простое, и p делит a·b, то p делит a или b.

Mалая теорема Ферма. Если p – простое, a – натуральное, то a p – a делится на p.

Теорема Вильсона. Натуральное p > 1 является простым тогда и только тогда, когда (p – 1)! + 1 делится на p.

Постулат Бертрана. Если n > 1 – натуральное, то существует простое p, такое, что n 1 – целые взаимно простые числа, содержит бесконечно много простых чисел.

Теорема Ферма. Каждое простое число вида 4k + 1 есть сумма двух квадратов натуральных чисел.

Всякое простое число, большее 3, представимо в виде 6k + 1 или 6k – 1, где k – некоторое натуральное число.

Число, следующее за простым, не может быть квадратом или более высокой степенью с основанием, большим 2.

Число, предшествующее простому, не может быть кубом или более высокой нечётной степенью с основанием, большим 1.

Задачи с решениями

1. Три простых числа, каждое из которых больше 10, образуют арифметическую прогрессию. Докажите, что разность прогрессии делится на 6.

Все данные простые числа нечётные, поэтому их разность делится на 2. Покажем, что она делится и на 3. Пусть данные числа a, a + d, a + 2d. Ни одно из них не делится на 3, поэтому при делении на 3 даёт остаток или 1, или 2. Следовательно, по крайней мере, два из этих чисел дают при делении на 3 одинаковые остатки. Разность этих чисел, равная d или 2d, делится на 3. Поскольку 2 на 3 не делится, то d делится на 3. Итак, разность прогрессии, которая делится на взаимно простые числа 2 и 3, делится на 6, что и требовалось доказать.

2. Докажите, что для произвольного натурального числа n найдётся натуральное m такое, что nm + 1 – составное число.

Можно выбрать m = n + 2, тогда

nm + 1 = n(n + 2) + 1 = n 2 + 2n + 1 = (n + 1) 2

является составным числом.

3. Найдите все целые числа n, для которых модуль значения трёхчлена n 2 – 7n + 10 будет простым числом.

|n 2 – 7n + 10| = |n –2| · |n – 5|,

то следует искать такие n при которых один из множителей последнего произведения равен 1, а второй является простым числом. Этому требованию удовлетворяют n = 3 и n = 4.

4. Докажите, что если числа

а) m и m 2 + 2 простые, то число m 3 + 2 тоже простое;

б) р, р – 10, р + 10 простые, то число р – 2 тоже простое.

а) Любое простое число m, отличное от 3, можно представить в виде 3n+1 или в виде 3n–1, где n – некоторое натуральное число. В первом случае можно записать

m 2 + 2 = 9n 2 + 6n +3,

m 2 + 2 = 9n 2 – 6n +3,

Так как m > 2, то в любом случае число m 2 +2 больше 3 и делится на 3, а значит является составным. Следовательно, число m 2 +2 может быть простым, только если m = 3. В этом случае m 2 +2 = 11 – простое число, m 3 +2 = 29 – тоже простое число, что и требовалось доказать.

б) Так как р – 10 = (р – 1) – 9 и р + 10 = (р + 1) + 9, то числа р – 10 и р – 1 при делении на 3 имеют одинаковые остатки, и числа р + 10 и р + 1 при делении на 3 имеют одинаковые остатки.

Из трёх последовательных чисел р – 1, р, р + 1 одно и только одно делится на 3. С учётом выше сказанного, то же утверждение верно для чисел р – 10, р, р + 10. Так как эти числа простые, то р – 10 = 3 и р = 13, поэтому р – 2 = 11 – простое число, что и требовалось доказать.

5. Сколько раз входит двойка в разложение на простые множители произведения

Ответ на поставленный вопрос получим из следующих преобразований:

6. Найдите все простые p такие, что число p 2 + 11 имеет ровно 6 различных делителей (включая единицу и само число).

Если p > 5 и простое, то числа p – 1 и p + 1 оба четные, и одно из них кратно трем. Поэтому произведение (p – 1)(p + 1) делится на 12, следовательно, p 2 + 11 также делится на 12, а значит, имеет не менее семи делителей (6 делителей числа 12 и само число p 2 + 11 > 12 ). Осталось проверить p = 2 и p = 3.

Если p = 2, то p 2 + 11 = 2 2 + 11 = 15 имеет 4 делителя (1, 3, 5, 15).

Если p = 3, то p 2 + 11 = 3 2 + 11 = 20 имеет 6 делителей (1, 2, 4, 5, 10, 20).

7. Найти все натуральные числа n, для которых каждое из шести чисел

n + 1, n + 3, n + 7, n + 9, n + 13 и n + 15

Рассмотрим варианты. Для n = 1 число n + 3 = 4 составное.

Для n = 2 число n + 7 = 9 составное.

Для n = 3 число n + 1 = 4 составное.

Для n > 4 все наши числа больше 5 и по крайней мере одно из них делится на 5, так как числа 1, 3, 7, 9, 13 и 15 при делении на 5 дают соответственно остатки 1, 3, 2, 4, 3 и 0, то есть все возможные остатки, откуда следует, что и числа

n + 1, n + 3, n + 7, n + 9, n + 13 и n + 15

при делении на 5 дают все возможные остатки и, следовательно, хотя бы одно из них делится на 5 и как число, большее пяти (так как n > 4), является составным.

Но для n = 4 мы получаем простые числа 5, 7, 11, 13, 17 и 19.

8. Доказать, что каждое простое число вида 4k + 1 является длиной гипотенузы прямоугольного треугольника, стороны которого выражаются натуральными числами.

9. Сколькими способами можно раскрасить круг, разбитый на р равных секторов с помощью n красок, если р – простое число и каждый сектор раскрашиваем одной краской? Две раскраски, совпадающие при повороте круга, считаем одинаковыми.

Каждый сектор можно раскрасить в любой из n цветов, поэтому для круга с р секторами получим n p раскрасок, среди которых (n p – n) не одноцветных. Каждая из этих раскрасок поворотами переходит в (р – 1) одинаковую с ней, значит, существенно различных не одноцветных раскрасок будет (n p – n)/p, откуда общее число раскрасок равно n + (n p – n)/p.

10. Доказать, что для любого простого числа p > 5 уравнение х 4 + 4 x = p в целых числах не имеет решений.

Докажем, что если для некоторого целого значения х число

является целым, то это число либо не превосходит пяти, либо является составным.

Действительно, если х 4 + 4 0 4 + 4 1 = 5.

Если x = 2k (k – натуральное число), то число

f(x) = 2 4 k 4 + 4 2k = 2 4 ( k 4 + 4 2(k–1) )

Наконец, если x = 2k + 1 (k – натуральное число), то число

f(x) = x 4 + 4·4 2k = (x 4 + 4x 2 (2 k ) 2 + 4(2 k ) 4 ) – 4x 2 (2 k ) 2 =

= (x 2 + 2(2 k ) 2 ) 2 – (2·x·2 k ) 2 =

= (x 2 + 2·x·2 k + 2(2 k ) 2 )·( x 2 – 2·x·2 k + 2(2 k ) 2 ) =

= ((x + 2 k ) 2 + 2 2k )·((x – 2 k ) 2 + 2 2k )

так же является составным, поскольку каждый из двух сомножителей последнего произведения больше 1 (ибо 2 2k > 1 при k > 0).

Таким образом, если число p > 5 простое, то равенство х 4 + 4 x = p не выполняется ни при каких целых значениях х.

Задачи без решений

1. Известно, что р, р + 10, р + 14 – простые числа. Найдите число р.

2. Докажите, что число

3. Найдите все простые р для которых число р 2 + 14 так же будет простым числом.

4. Докажите, что уравнение х 2 + х + 1 = р·у имеет решение в целых числах (х, у) для бесконечного числа простых р.

5. Введём обозначение для суммы первых n простых чисел через S_n:

Докажите, что между числами S_n и S_n+1 всегда существует число, являющееся полным квадратом.

Источник

Решение олимпиадных задач по темам «Делимость» и «Квадратный трёхчлен».

Решение олимпиадных задач

по темам «Делимость» и «Квадратный трёхчлен»

Урок-лекция Математическое творчество на примере темы «Делимость чисел».

За 1-2 часа невозможно показать всё многообразие идей и методов решения задач, особенно олимпиадных. На нашем занятии я хочу показать вам не только как решать задачи, но и показать, как они рождаются. Ведь придумать и решить свою новую задачу интереснее, чем решить готовую. Это творческий процесс, а Математика — это простор для полёта фантазии.

Начнём с разминки. Вы знаете, что все натуральные числа, кроме 1, делятся на простые и составные. Простые числа делятся нацело только на самих себя и на единицу. Если у числа есть хотя бы один другой (неравный самому себе и единице) делитель, то оно является составным. Доказать, что число простое гораздо труднее, чем доказать, что число составное. Приведу примеры.

Проверять число на простоту помогают признаки делимости. В школе изучаются многие из них, например, на 2,5,3,9. Несложные признаки делимости на 4 и 8. Из любой пары взаимно простых чисел можно получить путём их перемножения новые признаки: на 6 (если делится на 2 и 3) на 15 (если делится на 3 и 5). Подчеркну, что это работает только для взаимно простых пар. Утверждение: если число делится на 2 и на 4, то оно поделится на 8 неверно. Интересны признаки делимости на 7 и 11 – почитайте о них сами. Вообще, в теории чисел есть теорема Паскаля, которая позволяет найти признак делимости на любое число, правда для больших чисел проще посчитать в столбик, чем пользоваться этой теоремой.

№ 2. Можно ли получить пятизначное число простое число, переставляя цифры 1, 2, 3, 4 и 5? Сумма цифр в любом таком числе равна 15, значит, любое такое число поделится на 3, а, значит, будет составным, а простое получить нельзя. С этой задачей тесно связана такая задача.

№ 3. Запись натурального числа состоит из одной «1», двух «2 «, трёх «3» и т.д. девяти «9». Может ли оно быть точным квадратом? Его сумма цифр равна 285 делится на 3, но не делится на 9, а поэтому не может быть точным квадратом. Из этой же серии ещё одна задача.

Как-то на уроке я спросил, каким будет признак делимости на 6, а ученик ответил, что если сумма цифр делится на 6, то и само число делится на 6. Верно ли это утверждение? Нет, пример: 12. Но у меня в голове возникла задача (не исключено, что просто всплыла из памяти).

№ 6. Может ли число, делящееся на 8, при делении на 12 давать в остатке 10? Допустим, может. Тогда справедливо равенство: 8а=12в+10. Присмотримся к этому равенству: 8 и 12 оба делятся на 4, а 10 нет. Полученное противоречие доказывает, что такого числа не существует.

Вообще, математику всегда интересно решить задачу различными способами, рассмотреть для неё обратные задачи, обобщить полученное решение. Следуя этой схеме, рассмотрим

А может всё дело в том, что число k должно быть кратно 3? Появляется новая гипотеза.

Задачи на делимость часто встречаются на ЕГЭ (задача №19). Одну такую задачу я хочу показать вам, она тоже представляет собой маленькое исследование. В процессе её решения у меня возникало много вопросов. Попробуем вместе разобраться.

№ 12. Дано двузначное натуральное число.

а) Оказалось, что частное этого числа и суммы его цифр, равно 7. Найдите все такие числа.

б) Какие натуральные значения может принимать частное данного числа и суммы его цифр?

в) Какое наименьшее значение может принимать частное данного числа и суммы его цифр?

Решение. а) Пусть данное число 10х+у, его сумма цифр х+у. По условию составим уравнение: . Так как х и у – цифры, причём х  0, то условиям удовлетворяют числа: 21;42;63;84.

Источник