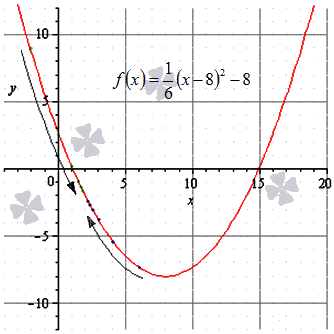
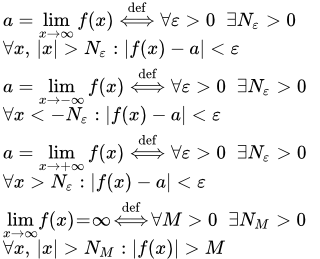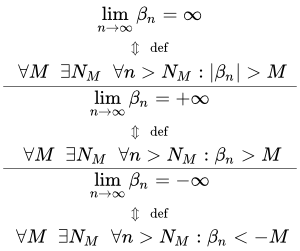доказать по определению что предел равен бесконечности

Определение предела функции на бесконечности

Конечный предел функции на бесконечности

Также часто используется следующее обозначение:
.

Запишем это определение, используя логические символы существования и всеобщности:
.
Здесь подразумевается, что значения принадлежат области определения функции.

Односторонние пределы

Часто встречаются случаи, когда функция определена только для положительных или отрицательных значений переменной x (точнее в окрестности точки или ). Также пределы на бесконечности для положительных и отрицательных значений x могут иметь различные значения. Тогда используют односторонние пределы.

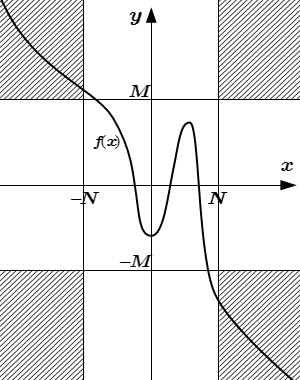
Бесконечный предел функции на бесконечности

С помощью логических символов существования и всеобщности, определение бесконечного предела функции можно записать так:
.

Аналогично вводятся определения бесконечных пределов определенных знаков, равных и :
.
.

Определения односторонних пределов на бесконечности.
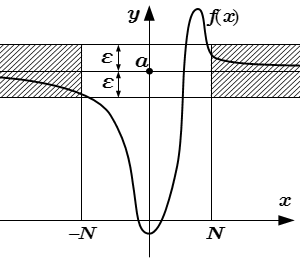
Левые пределы.
.
.
.
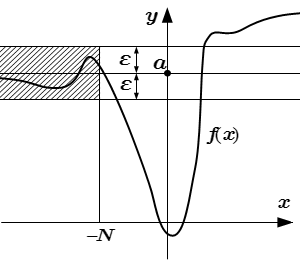
Правые пределы.
.
.
.

Определение предела функции по Гейне

Определения предела по Гейне и Коши эквивалентны.

Примеры

Пример 1

Все примеры ⇑ Используя определение Коши показать, что
.

Выпишем определение конечного предела функции на бесконечности по Коши:
.
Преобразуем разность:
.
Разделим числитель и знаменатель на и умножим на –1 :
.

Пример 2

1) Решение при x стремящемся к минус бесконечности

2) Решение при x стремящемся к плюс бесконечности

Преобразуем исходную функцию. Умножим числитель и знаменатель дроби на и применим формулу разности квадратов:
.
Имеем:

.
Выпишем определение правого предела функции при :
.

Использованная литература:
С.М. Никольский. Курс математического анализа. Том 1. Москва, 1983.

Источник

Математический анализ
Записки лекций

Илья Щуров (НИУ ВШЭ)

12 Бесконечные пределы и асимптоты

12.1 Бесконечные пределы в конечных точках

12.1.1 Существование предела и ограниченность

12.1.2 Бесконечные пределы

Опять же, аналогично последовательностям, помимо просто бесконечности, бывает плюс бесконечность и минус бесконечность:

Наконец, можно рассматривать односторонние бесконечные пределы.

12.2 Пределы на бесконечности

12.2.1 Конечные пределы на бесконечности и горизонтальные асимптоты

Верный ответ. Это правда. Например, у тангенса их бесконечно много.

Неверный ответ. У функции f ( x ) = 1 / ( x ( x − 1 ) ( x + 1 ) ) их три!

Неверный ответ. Что насчёт тангенса?

Неверный ответ. Этого не может быть из определения предела по Гейне.

Неверный ответ. А что вы можете сказать про последовательность < sin ( π n ) >? Найдите несколько её членов.

Неверный ответ. Этого не может быть из определения предела по Гейне.

12.2.2 Бесконечные пределы на бесконечности

12.2.3 Наклонные асимптоты

Как искать наклонные асимптоты? На эту тему есть рецепт.

Со вторым пределом ещё проще:

Источник

Определение бесконечно большой последовательности

Определение

Последовательности с пределами (2) и (3) являются частными случаями бесконечно большой последовательности (1). Из этих определений следует, что если предел последовательности равен плюс или минус бесконечности, то он также равен и бесконечности:
.
Обратное, естественно, не верно. Члены последовательности могут иметь чередующиеся знаки. При этом предел может равняться бесконечности, но без определенного знака.

Заметим также, что если какое-то свойство выполняется для произвольной последовательности с пределом равным бесконечности, то это же свойство выполняется и для последовательности, чей предел равен плюс или минус бесконечности.

Окрестности бесконечно удаленных точек

Когда мы рассматривали конечные пределы, то ввели понятие окрестности точки. Напомним, что окрестностью конечной точки является открытый интервал, содержащий эту точку. Также мы можем ввести понятия окрестностей бесконечно удаленных точек.

Теперь мы можем дать единое определение предела последовательности, которое относится как к конечным, так и к бесконечным пределам.

Таким образом, если предел существует, то за пределами окрестности точки a может находиться только конечное число членов последовательности, или пустое множество. Это условие является необходимым и достаточным. Доказательство этого свойства, точно такое, как для конечных пределов.

С помощью логических символов существования и всеобщности, это определение запишется так:
.

Примеры бесконечно больших последовательностей

Все примеры Сначала мы рассмотрим три простых похожих примера, а затем решим более сложный.

Пользуясь определением бесконечно большой последовательности показать, что
⇓, ⇓, ⇓, ⇓.

Пример 1

Все примеры ⇑ Пользуясь определением бесконечно большой последовательности показать, что
.

Пример 2

Все примеры ⇑ Пользуясь определением бесконечно большой последовательности показать, что
.

Пример 3

Все примеры ⇑ Пользуясь определением бесконечно большой последовательности показать, что
.

Пример 4

Все примеры ⇑ Пользуясь определением бесконечно большой последовательности показать, что
.

Использованная литература:
Л.Д. Кудрявцев. Курс математического анализа. Том 1. Москва, 2003.
С.М. Никольский. Курс математического анализа. Том 1. Москва, 1983.

Источник

Предел функции: основные понятия и определения

В этой статье мы расскажем, что из себя представляет предел функции. Сначала поясним общие моменты, которые очень важны для понимания сути этого явления.

Понятие предела

Если мы не можем определить ни конечное, ни бесконечное значение, это значит, что такого предела не существует. Примером этого случая может быть предел от синуса на бесконечности.

Что такое предел функции

В этом пункте мы объясним, как найти значение предела функции в точке и на бесконечности. Для этого нам нужно ввести основные определения и вспомнить, что такое числовые последовательности, а также их сходимость и расходимость.

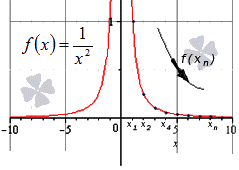
При x → ∞ предел функции f ( x ) является бесконечным, если последовательность значений для любой бесконечно большой последовательности аргументов будет также бесконечно большой (положительной или отрицательной).

Решение

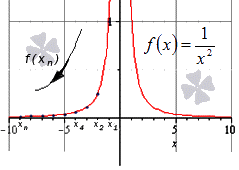
Далее мы запишем то же самое, но для бесконечно большой отрицательной последовательности.

Здесь тоже видно монотонное убывание к нулю, что подтверждает верность данного в условии равенства:

Ответ: Верность данного в условии равенства подтверждена.

Решение

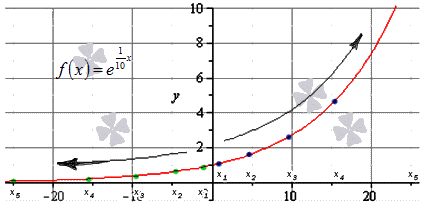
Мы видим, что данная последовательность бесконечно положительна, значит, f ( x ) = lim x → + ∞ e 1 10 x = + ∞

Наглядно решение задачи показано на иллюстрации. Синими точками отмечена последовательность положительных значений, зелеными ­ – отрицательных.

Перейдем к методу вычисления предела функции в точке. Для этого нам нужно знать, как правильно определить односторонний предел. Это пригодится нам и для того, чтобы найти вертикальные асимптоты графика функции.

Теперь сформулируем, что такое предел функции справа.

Теперь мы разъясним данные определения, записав решение конкретной задачи.

Решение

Значения функции в этой последовательности будут выглядеть так:

Чтобы более глубоко изучить теорию пределов, советуем вам прочесть статью о непрерывности функции в точке и основных видах точек разрыва.

Источник

Пределы в математике для чайников: объяснение, теория, примеры решений

Теория пределов – раздел математического анализа. Наряду с системами линейных уравнений и диффурами пределы доставляют всем студентам, изучающим математику, немало хлопот. Чтобы решить предел, порой приходится применять массу хитростей и выбирать из множества способов решения именно тот, который подойдет для конкретного примера.

В этой статье мы не поможем вам понять пределы своих возможностей или постичь пределы контроля, но постараемся ответить на вопрос: как понять пределы в высшей математике? Понимание приходит с опытом, поэтому заодно приведем несколько подробных примеров решения пределов с пояснениями.

Ежедневная рассылка с полезной информацией для студентов всех направлений – на нашем телеграм-канале.

Понятие предела в математике

Допустим, есть некоторая переменная величина. Если эта величина в процессе изменения неограниченно приближается к определенному числу a, то a – предел этой величины.

Для определенной в некотором интервале функции f(x)=y пределом называется такое число A, к которому стремится функция при х, стремящемся к определенной точке а. Точка а принадлежит интервалу, на котором определена функция.

Звучит громоздко, но записывается очень просто:

Существует также геометрическое объяснение определения предела, но здесь мы не будем лезть в теорию, так как нас больше интересует практическая, нежели теоретическая сторона вопроса. Когда мы говорим, что х стремится к какому-то значению, это значит, что переменная не принимает значение числа, но бесконечно близко к нему приближается.

Чтобы решить такой пример, подставим значение x=3 в функцию. Получим:

Кстати, если Вас интересуют базовые операции над матрицами, читайте отдельную статью на эту тему.

В примерах х может стремиться к любому значению. Это может быть любое число или бесконечность. Вот пример, когда х стремится к бесконечности:

Интуитивно понятно, что чем больше число в знаменателе, тем меньшее значение будет принимать функция. Так, при неограниченном росте х значение 1/х будет уменьшаться и приближаться к нулю.

Как видим, чтобы решить предел, нужно просто подставить в функцию значение, к которому стремиться х. Однако это самый простой случай. Часто нахождение предела не так очевидно. В пределах встречаются неопределенности типа 0/0 или бесконечность/бесконечность. Что делать в таких случаях? Прибегать к хитростям!

Неопределенности в пределах

Неопределенность вида бесконечность/бесконечность

Если мы попробуем в функцию подставить бесконечность, то получим бесконечность как в числителе, так и в знаменателе. Вообще стоит сказать, что в разрешении таких неопределенностей есть определенный элемент искусства: нужно заметить, как можно преобразовать функцию таким образом, чтобы неопределенность ушла. В нашем случае разделим числитель и знаменатель на х в старшей степени. Что получится?

Из уже рассмотренного выше примера мы знаем, что члены, содержащие в знаменателе х, будут стремиться к нулю. Тогда решение предела:

Для раскрытия неопределенностей типа бесконечность/бесконечность делим числитель и знаменатель на х в высшей степени.

Кстати! Для наших читателей сейчас действует скидка 10% на любой вид работы

Еще один вид неопределенностей: 0/0

В таких случаях рекомендуется раскладывать числитель и знаменатель на множители. Но давайте посмотрим на конкретный пример. Нужно вычислить предел:

Как всегда, подстановка в функцию значения х=-1 дает 0 в числителе и знаменателе. Посмотрите чуть внимательнее и Вы заметите, что в числителе у нас квадратное уравнение. Найдем корни и запишем:

Сократим и получим:

Итак, если Вы сталкиваетесь с неопределенностью типа 0/0 – раскладывайте числитель и знаменатель на множители.

Чтобы Вам было проще решать примеры, приведем таблицу с пределами некоторых функций:

Правило Лопиталя в пределах

Еще один мощный способ, позволяющий устранить неопределенности обоих типов. В чем суть метода?

Если в пределе есть неопределенность, берем производную от числителя и знаменателя до тех пор, пока неопределенность не исчезнет.

Наглядно правило Лопиталя выглядит так:

Важный момент : предел, в котором вместо числителя и знаменателя стоят производные от числителя и знаменателя, должен существовать.

А теперь – реальный пример:

Налицо типичная неопределенность 0/0. Возьмем производные от числителя и знаменателя:

Вуаля, неопределенность устранена быстро и элегантно.

Надеемся, что Вы сможете с пользой применить эту информацию на практике и найти ответ на вопрос «как решать пределы в высшей математике». Если нужно вычислить предел последовательности или предел функции в точке, а времени на эту работу нет от слова «совсем», обратитесь в профессиональный студенческий сервис за быстрым и подробным решением.

Иван Колобков, известный также как Джони. Маркетолог, аналитик и копирайтер компании Zaochnik. Подающий надежды молодой писатель. Питает любовь к физике, раритетным вещам и творчеству Ч. Буковски.

Источник