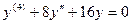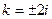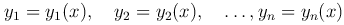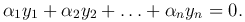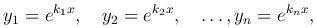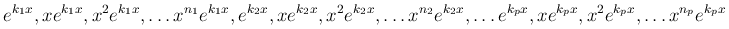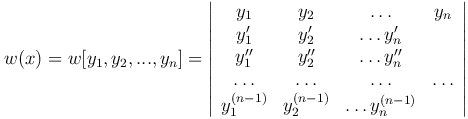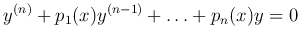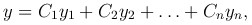доказать что функции линейно независимы
Линейно зависимые и линейно независимые функции. Примеры исследования функций на линейную зависимость по определению.
$$ \begin
Примечание к терминологии: показать\скрыть
Если же равенство (1) возможно лишь при условии:
Обоснование этого правила: показать\скрыть
Все примеры, указанные в этой теме, будут опираться на определения и свойство, приведенные выше. Естественно, что в общем случае применение таких определений несколько затруднительно. Существует несколько критериев, которые позволяют упростить процесс проверки функций на линейную зависимость. На сайте рассмотрены два таких способа: с помощью определителя Вронского и определителя Грама.
Раскроем скобки и перегруппируем слагаемые:
$$ \begin
$$\alpha_1\cdot 1+\alpha_2\cdot x+\alpha_3\cdot x^2+\alpha_4\cdot x^3+\alpha_5\cdot x^4=7x^3+2.$$
Т.е. в левой части равенства (4) может быть многочлен четвертого, третьего, второго, первого и нулевого порядков.
$$\alpha_1\cdot 1+\alpha_2\cdot x+\alpha_3\cdot x^2+\alpha_4\cdot x^3+\alpha_5\cdot x^4=\alpha_1$$
$$\arcsin x+\arccos x=\frac<\pi><8>\cdot4; \; \arcsin x+\arccos x-\frac<\pi><8>\cdot4=0; \; 1\cdot y_1+1\cdot y_2+\left(-\frac<\pi><8>\right)\cdot y_3=0$$
Исследование на линейную зависимость с помощью определителей Вронского и Грама указаны в дальнейших темах сайта.
Заметили ошибку, опечатку, или некорректно отобразилась формула? Отпишите, пожалуйста, об этом в данной теме на форуме (регистрация не требуется).
Линейная зависимость и линейная независимость функций
Понятие линейной независимости функций вводится аналогично понятию линейной независимости векторов.
называются линейно-зависимыми на отрезке [a, b], если существуют действительные числа α1, α2, …, αn, не все равные нулю (α²1+α²2+ … + α²n≠0), такие, что для любых x∈[a, b] выполняется равенство
линейно независимы на любом отрезке [a, b].
Определитель Вронского
Определение. Определителем Вронского называется определитель
с коэффициентами pk(x) (k=l, …, n), непрерывными на отрезке [a, b], то определитель Вронского w(x) = w[y1, y2, …, yn] не обращается в нуль ни в одной точке отрезка [a, b].
Общее решение линейного однородного уравнения n-го порядка
коэффициенты которого непрерывны на этом отрезке, то его общее решение определяется формулой
Следствие. Максимальное число линейно-независимых решений линейного однородного уравнения равно порядку этого уравнения.
Определение. Любые n линейно-независимых решений линейного однородного уравнения n-го порядка называются его фундаментальной системой решений.
Доказать линейную независимость системы функций

Доказать линейную независимость над R системы функций idR, x→ sinx, x→ cosx.
Доказать линейную независимость системы векторов
Помогите решить задачу из задачника по алгебре Кострикина. Вот задача: Пусть дана система векторов.
Доказать линейную независимость
Доказать, что система E:=
Проверьте, пожалуйста, доказательство:
Докажем линейную независимость на всей числовой оси функций
Докажем утверждение по индукции.
Пусть утверждение справедливо для k = 1:
k = 1, alpha1*e^x = 0, forall x => alpha1
Предположим теперь, что линейная независимость доказана для k − 1 функций
Разделим обе части равенства на exp(kx)
и продифференцируем последнее тождество по x:
Но входящие в равенство k − 1 функции по нашему индуктивному предположению линейно независимы и i − k ≠ 0. Следовательно, последнее равенство возможно только если все, входящие в него коэффициенты равны нулю:
Получили противоречие (предполагалось, что не все коэффициенты равны нулю). Это противоречие доказывает линейную независимость k функций. А отсюда, в свою очередь, по индукции следует линейная независимость всей исследуемой системы функций.
Линейная зависимость и независимость, свойства, исследование системы векторов на линейную зависимость, примеры и решения.
Понятия линейной зависимости и независимости системы векторов является очень важными при изучении алгебры векторов, так как на них базируются понятия размерности и базиса пространства. В этой статье мы дадим определения, рассмотрим свойства линейной зависимости и независимости, получим алгоритм исследования системы векторов на линейную зависимость и подробно разберем решения примеров.
Навигация по странице.
Определение линейной зависимости и линейной независимости системы векторов.
Так мы подошли к определению линейной зависимости системы векторов 
Если линейная комбинация 


Если линейная комбинация 


Свойства линейной зависимости и независимости.
На основании данных определений, сформулируем и докажем свойства линейной зависимости и линейной независимости системы векторов.
Если к линейно зависимой системе векторов 
Так как система векторов 



Добавим к исходной системе векторов еще s векторов 




представляет собой нулевой вектор, а 
Если из линейно независимой системы векторов 
Предположим, что полученная система линейно зависима. Добавив к этой системе векторов все отброшенные векторы, мы получим исходную систему векторов. По условию – она линейно независима, а в силу предыдущего свойства линейной зависимости она должна быть линейно зависимой. Мы пришли к противоречию, следовательно, наше предположение неверно.
Если в системе векторов 
Пусть вектор 





Если система векторов 

Сначала докажем первое утверждение.
Пусть система векторов 





Следовательно, вектор 

Теперь докажем второе утверждение.
Так как система векторов 


Предположим, что какой-нибудь вектор системы 




Из двух последних свойств следует важное утверждение:
если система векторов содержит векторы 


Исследование системы векторов на линейную зависимость.
Поставим задачу: нам требуется установить линейную зависимость или линейную независимость системы векторов 
Логичный вопрос: «как ее решать?»
Кое-что полезное с практической точки зрения можно вынести из рассмотренных выше определений и свойств линейной зависимости и независимости системы векторов. Эти определения и свойства позволяют нам установить линейную зависимость системы векторов в следующих случаях:
Как же быть в остальных случаях, которых большинство?
Напомним формулировку теоремы о ранге матрицы, которую мы приводили в статье ранг матрицы: определение, методы нахождения.
А теперь поясним связь теоремы о ранге матрицы с исследованием системы векторов на линейную зависимость.
Что будет означать линейная независимость системы векторов 
Что же будет означать линейная зависимость системы векторов 
Все очень просто: хотя бы одна строка матрицы A будет линейно выражаться через остальные, следовательно, линейная зависимость системы векторов 
Итак, задача исследования системы векторов на линейную зависимость сводится к задаче нахождения ранга матрицы, составленной из векторов этой системы.
Следует заметить, что при p>n система векторов 
Замечание: при составлении матрицы А векторы системы 
Алгоритм исследования системы векторов на линейную зависимость.
Разберем алгоритм на примерах.
Примеры исследования системы векторов на линейную зависимость.
Дана система векторов 
Так как вектор c нулевой, то исходная система векторов линейно зависима в силу третьего свойства.
система векторов линейно зависима.
Исследуйте систему векторов 
система векторов линейно зависима.
Является ли система векторов 
Является ли система векторов 
Докажите, что система векторов

линейно независима.
Составим матрицу, строками которой будут векторы данной системы:

Покажем, что ранг этой матрицы равен количеству векторов исходной системы, то есть, четырем.
Переходим к поиску окаймляющего минора третьего порядка:

Осталось найти минор четвертого порядка, отличный от нуля. Вычислим определитель

Прибавим к первому столбцу третий, далее разложим определитель по элементам первого столбца:

Таким образом, ранг матрицы А равен четырем что доказывает линейную независимость исходной системы векторов.
Мы ознакомились с понятиями и свойствами линейной зависимости и линейной независимости системы векторов, получили метод исследования системы векторов на линейную зависимость, преобразовали его в алгоритм, и подробно разобрали решения характерных примеров.
Лекция 20.
Линейная зависимость и независимость системы функций. Определитель Вронского, его свойства. Фундаментальная система решений однородного линейного дифференциального уравнения. Общее решение однородного уравнения.
Определение 20.1. Функции у1(х), у2(х),…, уп(х) называются линейно зависимыми на некотором отрезке [a,b], если существуют такие числа α1, α2,…, αп, хотя бы одно из которых не равно нулю, что
на рассматриваемом отрезке. Если же равенство (20.1) справедливо только при всех αi=0, функции у1(х), у2(х),…, уп(х) называются линейно независимымина отрезке [a,b].
Определение 20.2. Определитель вида
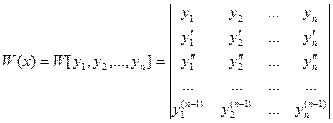
называется определителем Вронскогосистемы функций у1, у2,…, уп.
Теорема 20.1. Если функции у1, у2,…, уп линейно зависимы на отрезке [a,b], то их определитель Вронского на этом отрезке тождественно равен нулю.
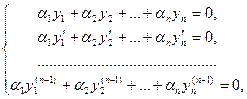
Теорема 20.2. Если линейно независимые функции у1, у2,…, уп являются решениями линейного однородного уравнения (19.2) с непрерывными на отрезке [a,b] коэффициентами, то определитель Вронского для этих функций не может обратиться в нуль ни в одной точке отрезка [a,b].
Пусть 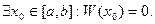
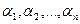
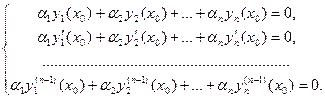
(Определитель этой системы, неизвестными в которой считаем 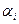

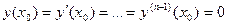
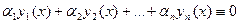

Замечание. В теореме 20.2 важно, что функции у1, у2,…, уп – решения уравнения (19.2). Для произвольной системы функций утверждение теоремы не справедливо.
Теорема 20.3. Общим решением на [a,b] уравнения (19.2) с непрерывными коэффициентами pi является линейная комбинация 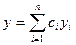
Доказательство. Для доказательства теоремы с учетом теоремы существования и единственности достаточно показать, что можно подобрать постоянные ci так, чтобы удовлетворялись произвольно заданные начальные условия:
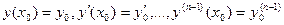
Подставив в равенства (20.6) выражение для у вида (20.5), получим линейную систему из п уравнений относительно неизвестных с1, с2,…, сп:
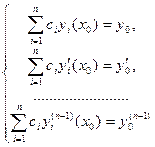
определителем которой является определитель Вронского для выбранных п линейно независимых решений рассматриваемого уравнения, который по теореме 20.2 не равен нулю. Следовательно, по правилу Крамера система имеет решение при любых правых частях. Теорема доказана.
Следствие. Максимальное число линейно независимых решений однородного уравнения (19.2) равно его порядку.
Определение 20.3. Любые п линейно независимых решений однородного линейного уравнения (19.2) называются его фундаментальной системой решений.
Таким образом, общее решение уравнения (19.2) является линейной комбинацией любой его фундаментальной системы решений.
Однородные линейные дифференциальные уравнения с постоянными коэффициентами. Построение фундаментальной системы решений. Неоднородные линейные дифференциальные уравнения. Частное и общее решения.
Определим вид частных решений однородного линейного уравнения
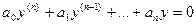
в котором коэффициенты ai постоянны. Можно показать, что они имеют вид 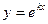
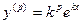
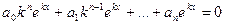
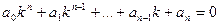
так называемое характеристическое уравнение для уравнения (21.1). Числа k, являющиеся его решениями, при подстановке в функцию 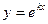
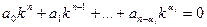
а соответствующее дифференциальное уравнение:
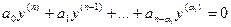
Очевидно, что частными решениями такого уравнения будут функции 1,x, x²,…, 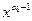
Пусть теперь корень характеристического уравнения ki кратности αi не равен нулю. Сделаем замену переменной: 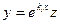
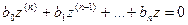
При этом корни характеристического уравнения
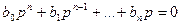
отличаются от корней уравнения
Таким образом, каждый кратный корень уравнения (21.2) задает серию линейно независимых частных решений уравнения (21.1), количество которых равно его кратности. Следовательно, вновь построена фундаментальная система решений.
Замечание. Кратные комплексно сопряженные корни задают частные решения вида 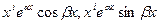
2. Для уравнения