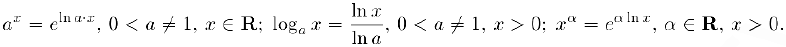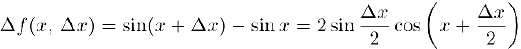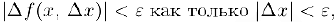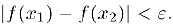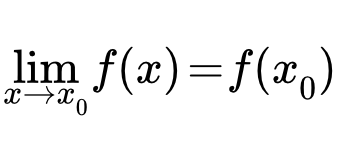доказать что функция не является равномерно непрерывной
Непрерывность элементарных функций
Непрерывность элементарных функций
Докажем, что любая элементарная функция непрерывна всюду, где она определена. Как следует из общих свойств непрерывности (пункт 1) для этого достаточно доказать, что непрерывными в своей области определения являются основные элементарные функции.
Непрерывность экспоненты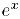 
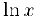
и натурального логарифма 
(равенства (1)). Отсюда на основании свойств 1), 2) непрерывности (пункт 1) немедленно следует непрерывность функций
Осталось доказать непрерывность тригонометрических и обратных тригонометрических функций. Рассмотрим приращение функции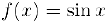 
в произвольной точке x:
Из неравенства (1), §4, пункт 3 следует, что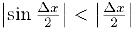 
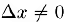
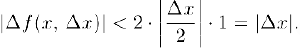
при малых 
. поэтому, 
.
Отсюда мы заключаем, что при любом заданном 
т. е.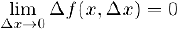 
. что и означает непрерывность функции sin x.
Непрерывность остальных тригонометрических функций следует из соотношений
и уже упоминавшихся общих свойств непрерывности (пункт 1).
Для доказательства непрерывности обратных тригонометрических функций достаточно сослаться на теорему о непрерывности обратной функции из предыдущего пункта.
Равномерная непрерывность функции
Определение. Функция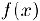 
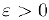
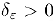
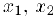
называется равномерно непрерывной на некотором промежутке числовой оси (конечном, или бесконечном), если она определена на этом промежутке и для любого положительного числа 
найдется положительное число 
, обладающее тем свойством, что при всех 
из данного промежутка, удовлетворяющих неравенству
для соответствующих значений функции выполняется неравенство
Покажем что равномерная непрерывность является более, сильным свойством функции, чем ее непрерывность на промежутке. Действительно, если функция равномерно непрерывна па некотором промежутке, то, зафиксировав произвольную точку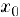 
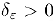
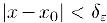
, этого промежутка, мы получим, что для любого отыщется такое, что 
как только 
, что и означает непрерывность функции на данном промежутке. Убедимся теперь на примере в том. что из непрерывности функции на промежутке еще не следует, вообще говоря, равномерная непрерывность.
Эта лекция взята со страницы онлайн помощи по математическому анализу:
Возможно эти страницы вам будут полезны:
Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
Равномерная непрерывность и модуль непрерывности
Равномерная непрерывность
Равномерная непрерывность. Модуль непрерывности. Если функция / непрерывна на отрезке, это означает, что для любой точки x этого отрезка и для любого числа e все точки x ’отрезка (в зависимости от точки x и числа e) равны. \ х ’-х | 8,(6.13） 228. Неравенство сохраняется. Я /(* ’)-А (х)| е.(6.14 )） Если вы можете выбрать число 6.13 независимо от точки x, так что условие (6.14) выполняется, когда выполняется условие (), то функция A называется равномерной непрерывностью. Остановимся далее на определении этого важного понятия. Определение 3.Функция a, определяемая отрезком[a, b], имеет произвольные 2 точки X∈[a, b]и x ’ε[a, b]существует 8 \ x ’-x | 8, неравенство| /(x ’)-/(x)| e. В символьной нотации определение непрерывности функций на отрезке выглядит следующим образом: V x V e 3 8 V x’, | x’ x / 8. | / (x’) /(x) / e, и определение равномерной непрерывности является: V e 3 8 V x, x’, | x’ x / 8. | /(х ’)-/(х)| е.(6.15 )） Где точки x и x ’принадлежат отрезку, на котором рассматривается функция/.
Ясно, что все функции, равномерно смежные через равные промежутки времени, являются смежными. Людмила Фирмаль
Это равенство для фиксированного Hfor Это [/(Х + З)-/(х)] = К [(Х + З) 2-Х2] = х ® идти х ® перейти = Он(2хв + Н2)= идти. х ® идти Итак, если дано e, то, что бы ни было 8, зафиксируйте HΦ, / H / 8, неравенство| /(x + H)-/(x)| e. Т Е О Р Е М А 5 (Кантор).Функции, непрерывные на отрезке равномерно непрерывной на отрезке. Доказательство. Докажем теорему противоречием. Предположим, что существует непрерывная функция в некотором интервале[a, b], но она не является равномерно непрерывной на it. It точки x∈[a, B]и x ’€[a, b]для любых 8,| x’-x / 8, но / f (x ’) A (x) e. In в частности, если 8 = 1 / n, есть точки, которые указывают на них в xn и x’N. \ хп-хп \ Н,(6.Шесть） Но… | /(хп)-/(хп)| электронная. (6.17 )） Из столбца
Условия равномерной непрерывности могут быть сформулированы относительно так называемых колебаний функций на отрезках. Людмила Фирмаль
Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
Равномерная непрерывность функций. Модуль непрерывности
Равномерная непрерывность функций. Модуль непрерывности
Равномерная непрерывность функций. Модуль непрерывности. Помимо понятия непрерывности функций в одной точке большую роль в математическом анализе играет так называемое понятие равномерной непрерывности функций на множестве. Определение 9.Функция f (x), определяемая множеством c C Hn, имеет δ=δ (ε) 0 для любого ε0 и для любых 2 точек Заметим, что если функция / равномерно непрерывна на множестве E, то она просто непрерывна на E, т. е. непрерывна в каждой точке x (0)∈E. To проверьте это, поставьте например (19.10) и (19.11) Если функция / непрерывна в каждой точке x E C, то для E0 она равна только 6 = 6 (e; x), поэтому все x’es удовлетворяют условию p (x, x’) 6, отсюда неравенство| / (x)-/(x ’)| e. In в этом случае выбор b зависит не только от e, но и от точки x в общих чертах.
Если вы описываете указанное определение с помощью логического символа, предыдущее содержимое отображается четко. Людмила Фирмаль
Например, точка формы (n-достаточно большое натуральное число)| x-x ’| 6, в то же время| /(x)-/(x’) | 1. В качестве достаточного указания на равномерную непрерывность функций 1 переменной на интервале отметим следующее. Лемма 2.Если функция f (x) определена и имеет ограниченный дифференциал в одном интервале (a, b), то она равномерно непрерывна в этом интервале. Фактически, если в (a, b) это\ [’(x)\(c-константа), то используя формулу конечных лагранжевых приращений (см.§ 11.2、 Так, для Е0, б = е / с вполне достаточно. Тогда Х ’ Х! Б, х б, кулер ACX ’ЦБ, затем (19.12), в\ неравенство <(х’)-[(х)\ е проводит. То есть функция / равномерно смежна с(a, b). Г] Аналогичные результаты применимы к конечным или бесконечным произвольным интервалам. Обобщение этого критерия для многомерных случаев описано в§ 39.2. Следующие теоремы имеют фундаментальное значение.
Другой подход к концепции равномерной непрерывности часто оказывается более удобным. Людмила Фирмаль
Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
Как доказать непрерывность функции
Пример 1: докажите непрерывность функции f(x) = x^2 в точке x_0.
По ε-Δ определению существует такое ε > 0, что |x^2 – x_0^2|
Некоторые элементарные функции являются непрерывными на всей области определения (множестве значений X):
Пример 2: докажите непрерывность функции f(x) = sin x.
По определению непрерывности функции по ее бесконечно малому приращению запишите:
Преобразуйте по формуле для тригонометрических функций:
Δf = 2*cos((x + Δx)/2)*sin(Δx/2).
Функция cos ограничена при x ≤ 0, а предел функции sin(Δx/2) стремится к нулю, следовательно, она является бесконечно малой при Δx→0. Произведение ограниченной функции и бесконечно малоq величины, а значит и приращение исходной функции Δf также является бесконечной малой величиной. Следовательно, функция f(x) = sin x непрерывна для любого значения x.
Пример 1: докажите непрерывность функции f(x) = x^2 в точке x_0.
По ε-Δ определению существует такое ε > 0, что |x^2 – x_0^2|
Некоторые элементарные функции являются непрерывными на всей области определения (множестве значений X):
Пример 2: докажите непрерывность функции f(x) = sin x.
По определению непрерывности функции по ее бесконечно малому приращению запишите:
Преобразуйте по формуле для тригонометрических функций:
Δf = 2*cos((x + Δx)/2)*sin(Δx/2).
Функция cos ограничена при x ≤ 0, а предел функции sin(Δx/2) стремится к нулю, следовательно, она является бесконечно малой при Δx→0. Произведение ограниченной функции и бесконечно малоq величины, а значит и приращение исходной функции Δf также является бесконечной малой величиной. Следовательно, функция f(x) = sin x непрерывна для любого значения x.
Некоторые элементарные функции являются непрерывными на всей области определения (множестве значений X):
Пример 2: докажите непрерывность функции f(x) = sin x.
По определению непрерывности функции по ее бесконечно малому приращению запишите:
Преобразуйте по формуле для тригонометрических функций:
Δf = 2*cos((x + Δx)/2)*sin(Δx/2).
Функция cos ограничена при x ≤ 0, а предел функции sin(Δx/2) стремится к нулю, следовательно, она является бесконечно малой при Δx→0. Произведение ограниченной функции и бесконечно малоq величины, а значит и приращение исходной функции Δf также является бесконечной малой величиной. Следовательно, функция f(x) = sin x непрерывна для любого значения x.
Непрерывность функций – теоремы и свойства
Определение непрерывности функции
Определение непрерывности справа (слева)
Функция f ( x ) называется непрерывной справа (слева) в точке x 0 , если она определена на некоторой правосторонней (левосторонней) окрестности этой точки, и если правый (левый) предел в точке x 0 равен значению функции в x 0 :
.
Свойства непрерывных в точке функций
Свойство непрерывности слева и справа
Функция непрерывна в точке тогда и только тогда, когда она непрерывна в справа и слева.
Доказательства свойств приводятся на странице «Свойства непрерывных в точке функций».
Непрерывность сложной функции
Предел сложной функции
Точки разрыва
Определение точки разрыва 1-го рода
Точка называется точкой разрыва первого рода, если является точкой разрыва и существуют конечные односторонние пределы слева и справа :
.
Определение скачка функции
Скачком Δ функции в точке называется разность пределов справа и слева
.
Таким образом, точка устранимого разрыва – это точка разрыва 1-го рода, в которой скачек функции равен нулю.
Определение точки разрыва 2-го рода
Точка называется точкой разрыва второго рода, если она не является точкой разрыва 1-го рода. То есть если не существует, хотя бы одного одностороннего предела, или хотя бы один односторонний предел в точке равен бесконечности.
Свойства функций, непрерывных на отрезке
Вторая теорема Вейерштрасса о максимуме и минимуме непрерывной функции
Непрерывная на отрезке функция достигает на нем своих верхней и нижней граней или, что тоже самое, достигает на отрезке своего максимума и минимума.
Обратные функции
Аналогичным образом можно сформулировать теорему о существовании и непрерывности обратной функции на полуинтервале.
Свойства и непрерывность элементарных функций
Элементарные функции и обратные к ним непрерывны на своей области определения. Далее мы приводим формулировки соответствующих теорем и даем ссылки на их доказательства.
Показательная функция
Логарифм
Экспонента и натуральный логарифм
Степенная функция
Тригонометрические функции
Теорема о непрерывности тригонометрических функций
Тригонометрические функции: синус ( sin x ), косинус ( cos x ), тангенс ( tg x ) и котангенс ( ctg x ), непрерывны на своих областях определения.
Теорема о непрерывности обратных тригонометрических функций
Обратные тригонометрические функции: арксинус ( arcsin x ), арккосинус ( arccos x ), арктангенс ( arctg x ) и арккотангенс ( arcctg x ), непрерывны на своих областях определения.
Использованная литература:
О.И. Бесов. Лекции по математическому анализу. Часть 1. Москва, 2004.
Л.Д. Кудрявцев. Курс математического анализа. Том 1. Москва, 2003.
С.М. Никольский. Курс математического анализа. Том 1. Москва, 1983.