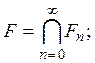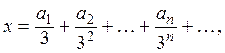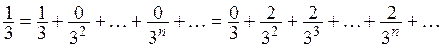доказать что множество открыто

Замкнутые и открытые множества

Одна из основных задач теории точечных множеств — изучение свойств различных типов точечных множеств. Познакомимся с этой теорией на двух примерах и изучим свойства так называемых замкнутых и открытых множеств.

Приведем примеры замкнутых и открытых множеств. Всякий отрезок есть замкнутое множество, а всякий интервал — открытое множество. Несобственные полуинтервалы и замкнуты, а несобственные интервалы и открыты. Вся прямая является одновременно и замкнутым и открытым множеством. Удобно считать пустое множество тоже одновременно замкнутым и открытым. Любое конечное множество точек на прямой замкнуто, так как оно не имеет предельных точек. Множество, состоящее из точек

Наша задача состоит в том, чтобы выяснить, как устроено произвольное замкнутое или открытое множество. Для этого нам понадобится ряд вспомогательных фактов, которые мы примем без доказательства.

1. Пересечение любого числа замкнутых множеств замкнуто.

2. Сумма любого числа открытых множеств есть открытое множество.

3. Если замкнутое множество ограничено сверху, то оно содержит свою верхнюю грань. Аналогично, если замкнутое множество ограничено снизу, то оно содержит свою нижнюю грань.

4. Если множество замкнуто, то его дополнение открыто и обратно.

Предложение 4 показывает, что между замкнутыми и открытыми множествами имеется весьма тесная связь: одни являются дополнениями других. В силу этого достаточно изучить одни замкнутые или одни открытые множества. Знание свойств множеств одного типа позволяет сразу выяснить свойства множеств другого типа. Например, всякое открытое множество получается путем удаления из прямой некоторого замкнутого множества.

В силу предложения 4, отсюда сразу вытекает, что всякое открытое множество на прямой представляет собой не более чем счетную сумму непересекающихся интервалов. В силу предложений 1 и 2, ясно также, что всякое множество, устроенное, как указано выше, действительно является замкнутым (открытым).

Как видно из нижеследующего примера, замкнутые множества могут иметь весьма сложное строение.

Канторово совершенное множество

Рассмотрим некоторые свойства этого множества. Множество замкнуто, так как оно образуется путем удаления из прямой некоторого, множества непересекающихся интервалов. Множество не пусто; во всяком случае в нем содержатся концы всех выброшенных интервалов.

Можно показать, что множество имеет мощность континуума. В частности, отсюда следует, что канторово совершенное множество содержит, кроме концов смежных интервалов, еще и другие точки. Действительно, концы смежных интервалов образуют лишь счетное множество.

Разнообразные типы точечных множеств постоянно встречаются в самых различных разделах математики, и знание их свойств совершенно необходимо при исследовании многих математических проблем. Особенно большое значение имеет теория точечных множеств для математического анализа и топологии.

Исследования Н.Н. Лузина и его учеников показали, что имеется глубокая связь между дескриптивной теорией множеств и математической логикой. Трудности, возникающие при рассмотрении ряда задач дескриптивной теории множеств (в частности, задач об определении мощности тех или иных множеств), являются трудностями логической природы. Напротив, методы математической логики позволяют более глубоко проникнуть в некоторые вопросы дескриптивной теории множеств.

Источник

Математика, физика на «отлично»

Открытые и замкнутые множества

В курсе математического анализа на первом курсе ВУЗов встречается много непонятного и непривычного. Одна из первых таких «новых» тем — это открытые и замкнутые множества. Постараемся дать пояснения по данной тематике.

Перед тем, как приступить к постановке определений и задач, напомним значение используемых обозначений и кванторов :
∈ — принадлежит
∅ — пустое множество
Ε — множество действительных чисел
х* — закреплённая точка
А* — множество граничных точек
: — такое, что
⇒ — следовательно
∀ — для каждого
∃ — существует
U_ε(х) — окрестность х по ε
Uº_ε(х) — проколотая окрестность х по ε

Итак,
Определение 1: Множество М ∈ Ε называется открытым, если для любого у ∈ М найдётся такое ε > 0, что окрестность y по ε строго меньше М
С помощью кванторов определение запишется следующим образом:
М ∈ Ε — открытое, если ∀ у∈М ∃ ε>0 : U_ε(y) Определение 2: Точка x* ∈ E называется граничной точкой множества М, если в любой окрестности точки х содержатся точки как из множества М, так и из его дополнения.
Теперь с помощью кванторов:
х*∈ E — граничная точка, если ∀U_ε(x) ∩ М ≠ ∅ и ∀U_ε(x) ∩ Е\М

Определение 3: Множество называется замкнутым, если ему принадлежат все граничные точки. Пример — отрезок [a, b]

Стоит отметить, что существуют множества, которые одновременно и открытые, и замкнутые. Это, например, всё множество действительных чисел и пустое множество (позднее будет доказано, что это 2 возможных и единственных случая).

Докажем несколько теорем, связанных с открытым и замкнутым множествами.

Теорема 1: Пусть множество А — открытое. Тогда дополнение к множеству А является замкнутым множеством.
Доказательство: Обозначим дополнение множества А как множество В:
В = Е\А
Доказывать будем от противного.
Предположим, что В — незамкнутое. Тогда существует граничная точка х*, которая не принадлежит В, а значит — принадлежит А. По определению граничной точки окрестность х* имеет пересечение как с В, так и с А. Однако с другой стороны х* является внутренней точкой открытого множества А, поэтому вся окрестность точки х* лежит в А. Отсюда делаем вывод, что множества А и В пересекаются не по пустому множеству. Такого быть не может, поэтому наше предположение неверно и В является замкнутым множеством, ч. т. д.
В кванторах доказательство можно записать короче:
Предположим, что В — незамкнутое, тогда:
(1) ∃ х∈А*:х∈A ⇒ ∀U_ε(x) ∩ В ≠ ∅ (определение граничной точки)
(2) ∃ х∈А*:х∈A ⇒ ∀U_ε(x) ⊂ А ≠ ∅ (определение открытоко множества)
Из (1) и (2) ⇒ А ∩ В ≠ ∅. Но А ∩ В = А ∩ Е\А = 0. Противоречие. В — замкнутое, ч. т. д.

Теорема 2: Пусть множество А — замкнутое. Тогда дополнение к множеству А является открытым множеством.
Доказательство: Обозначим дополнение множества А как множество В:
В = Е\А
Доказывать будем от противного.
Предположим, что В — замкнутое множество. Тогда любая граничная точка лежит в В. Но так как А — также замкнутое множество, то все граничные точки принадлежат и ему. Однако точка не может одновременно принадлежать множеству и его дополнению. Противоречие. В — открытое множество, ч. т. д.
В кванторах это выглядеть будет следующим образом:
Предположим, что В — замкнутое, тогда:
(1) ∀ х∈А*:х∈A (из условия)
(1) ∀ х∈А*:х∈В (из предположения)
Из (1) и (2) ⇒ А ∩ В ≠ ∅. Но А ∩ В = А ∩ Е\А = 0. Противоречие. В — открытое, ч. т. д.

Теорема 3: Пусть множество А — замкнутое и открытое. Тогда А = Е или А = ∅
Доказательство: Начнём записывать подробно, но сразу использую кванторы.
Предположим, что множество С — замкнутое и открытое, причём С ≠ ∅ и С ≠ Е. Тогда очевидно, что С ⊆ Е.
(1) ∃ х∈А*:х∈С ⇒ ∀U_ε(x) ∩ Е\С ≠ ∅ (определение граничной точки, которая принадлежит С)
(2) ∃ х∈А*:х∈A ⇒ ∀U_ε(x) ⊂ В (определение открытого множества С)
Из (1) и (2) следует, что Е\С ∩ С ≠ ∅, но это неверно. Противоречие. С не может быть одновременно и открытым, и замкнутым, ч. т. д.

Математический анализ — это фундаментальная математика, сложная и непривычная для нас. Но надеюсь, что-то стало понятнее после прочтения статьи. В добрый путь!

Источник

§1 определение и примеры метрических пространств

§6. Теоремы об открытых и замкнутых множествах

Теорема 1. Объединение любого числа открытых множеств – множество открытое.

Пусть G k – открытые множества.

Докажем, что – открытое множество.

Получили, что любая точка х о  G – внутренняя, а это означает, что G – открытое множество. 

Пусть G k ( k = 1,2, …, n ) – открытые множества.

Докажем, что – открытое множество.

Замечание 1. Пересечение бесконечного числа открытых множеств может и не быть аоткрытым множеством.

Пусть F k – замкнутые множества.

Докажем, что множества замкнутое, т.е. оно содержит все свои предельные точки.

Теорема 4. Объединение конечного числа замкнутных непустых множеств– замкнутое множество.

Пусть множества F k – замкнутые.

Замечание 2. Объединение бесконечного числа замкнутых множеств может быть множеством открытым.

§7. Последовательности точек метрического пространства

Определение 4. Пусть ( x n ) – последовательность точек метрического пространства ( Х,  ). Точка а  Х называется пределом последовательности ( x n ) если:

Если последовательность ( x n ) имеет конечный предел, то она называется сходящейся, в противном случае – расходящейся.

Обратное не всегда имеет место.

Для сходящихся последовательностей справедливы теоремы.

Теорема 1. Если ( x n ) – сходящаяся последовательность метрического пространства ( Х,  ), то её предел единственный.

§8. Свойства сходящихся последовательностей в некоторых

Теорема 1 ( о покоординатной сходимости последовательности в м. пр. R m ). Для того, чтобы последовательность точек метрического пространства R m

Если выполняются равенства (1), то говорят, что последовательность ( х n ) сходится к точке а покоординатно.

Докажем, что выполняются равенства (1).

В силу равенства (2) (по определению предела последовательности) в м.пр. R m будем иметь:

2. Пусть выполняются равенства (1).

Теорема 2 ( Больцана-Вейерштрасса в м.пр. R m ). Из всякой ограниченной последовательности пространства R m можно выделить сходящуюся подпоследовательность.

Чвстный случай этой теоремы для пространства R 1 был доказан на первом курсе.

Докажем с помощью критерия равномерной сходимости.

Известно, что фукциональная последовательность ( x n ) равномерно сходится да предельной фукции х тогда и только тогда, когда

Замечание 1. Поскольку любая норма задает метрику,

то в нормированном пространстве А также можно определить предел последовательности элементов нормированного пространства.

§9. Полные метрические пространства

Примером фундаментальной последовательности является любая сходящаяся последовательность точек метрического пространства.

В пространстве R любая фундаментальная последовательность – сходящаяся. Но для любого м.пр. не всякая фундаментальная последовательность метрического пространства ( Х,  ) сходится в этом пространстве.

Па определению фундаментальной последовательности и определению метрики в пространстве R m

По определению фундаментальной последовательности

Таким образом, мы доказали, что

0 N  N  m,n > N  x ( t )  x n ( t )    t  [ a,b ].

Банохавыми пространствоми, являются пространства:

Примерами гильбертовых пространств являются перечисленные пространства из примеров §4. Предгильбертовое пространство из примера 3 §4 не является полным относительно нормы (2) и поэтому не является гильбертовым.

Источник

(6) Хотя многие основные понятия переносятся с метрических пространств на топологические пространства, определенные в (4), в ряде случаев это понятие оказывается слишком общим. Важнейшим частным случаем топологических пространств являются те пространства, в которых наряду с аксиомами 1° и 2° выполняется еще так называемая аксиома отделимости Хаусдорфа:

3°. Любые две различные точки хну пространства Т имеют непересекающиеся окрестности.

Топологическое пространство, удовлетворяющее этой аксиоме, называется Хаусдорфовым топологическим пространством. Очевидно, что всякое метрическое пространство является Хаусдорфовым. Пространство, указанное в примере (4-6), не удовлетворяет аксиоме Хаусдорфа.

§11. Открытые и замкнутые множества на прямой

Структура открытых и замкнутых множеств в произвольном метрическом пространстве может быть весьма сложной. Мы рассмотрим сейчас простейший частный случай, а именно — открытые и замкнутые множества на прямой. В этом случае их полное описание не представляет большого труда и дается следующей теоремой.

Теорема 1. Всякое открытое множество на числовой прямой представляет собой сумму конечного или счетного числа попарно непересекающихся интервалов[4].

Доказательство. Пусть G — открытое множество и Тогда, по определению открытого множества, найдется некоторый интервал I, содержащий точку х и целиком принадлежащий множеству G. Этот интервал можно всегда выбрать так, чтобы его концы были рациональными. Взяв для каждой точки соответствующий интервал I, мы получим покрытие множества G счетной системой интервалов (эта система счетна, так как множество всех интервалов с рациональными концами счетно). Далее мы скажем, что интервалы I’ и I» (из нашего покрытия) принадлежат одному классу, если существует такая соединяющая их конечная цепочка интервалов:

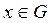
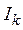
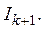
(принадлежащих нашему покрытию), что пересекается с Ясно, что таких классов будет конечное или счетное число. Далее, объединение всех интервалов, принадлежащих одному и тому же классу, представляет собой, очевидно, опять-таки некоторый интервал U, и интервалы, соответствующие различным классам, не пересекаются. Теорема доказана.

Так как замкнутые множества — это дополнения открытых, то отсюда следует, что всякое замкнутое множество на прямой получается выбрасыванием из прямой конечного или счетного числа интервалов.

Простейшие примеры замкнутых множеств — отрезки, отдельные точки и суммы конечного числа таких множеств. Рассмотрим более сложный пример замкнутого множества на прямой, так называемое канторово множество.

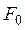
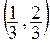
Пусть — отрезок [0, 1]. Выбросим из него интервал и оставшееся замкнутое множество обозначим

Затем выбросим из интервалы и и оставшееся замкнутое множество (состоящее из четырех отрезков) обозначим В каждом из этих четырех отрезков выбросим средний интервал длины и т. д. Продолжая этот процесс, получим убывающую последовательность замкнутых множеств Положим,

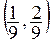
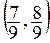
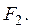
F — замкнутое множество (как пересечение замкнутых). Оно получается из отрезка [0, 1] выбрасыванием счетного числа интервалов. Рассмотрим структуру множества F. Ему принадлежат, очевидно, точки

(1)

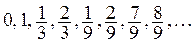
концы выбрасываемых интервалов. Однако множество F не исчерпывается этими точками. Действительно, те точки отрезка [0, 1], которые входят в множество F, можно охарактеризовать следующим образом. Запишем каждое из чисел 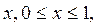по троичной системе:

где числа могут принимать значения 0, 1 и 2. Как и в случае обычных десятичных дробей, некоторые числа допускают двоякую запись. Например,

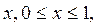
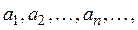
Легко проверить, что множеству F принадлежат те и только те числа которые могут быть записаны, хотя бы одним способом, в виде троичной дроби так, чтобы в последовательности единица ни разу не встречалась. Таким образом каждой точке можно поставить в соответствие последовательность

(2)

Источник

Пересечение любого конечного семейства открытых множеств есть открытое множество.

Доказательство.

1) Действительно, если точка а принадлежит объединению открытых множеств, то она принадлежит по крайней мере, одному из этих множеств, которое по условию теоремы является открытым. Значит, ему принадлежит некоторая окрестность О(а) точки а, но тогда эта окрестность принадлежит и объединению всех открытых множеств. Следовательно, точка а является внутренней точкой объединения. Так как а – произвольная точка объединения, то оно состоит лишь из внутренних точек, и, значит, по определению является открытым множеством.

2) Пусть теперь Х – пересечение конечного числа открытых множеств . Если а есть точка множества Х, то она принадлежит каждому из открытых множеств , и, следовательно, является внутренней точкой каждого из открытых множеств. Другими словами, существуют интервалы , которые целиком содержатся соответственно в множествах . Обозначим через наименьшее из чисел . Тогда интервал будет содержаться одновременно во всех интервалах , т.е. будет целиком содержаться и в , и в . и в , т.е. . Отсюда заключаем, что любая точка является внутренней точкой множества Х, т.е. множество Х является открытым.

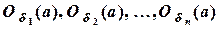
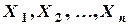
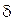
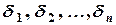
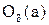
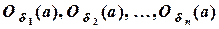
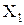
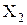
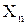
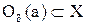
Из этой теоремы следует, что пересечение конечного числа окрестностей точки а есть опять окрестность этой точки. Заметим, что пересечение бесконечного числа открытых множеств не всегда является открытым множеством. Например, пересечением интервалов ,… является множеством, состоящее из одной точки а, которое, не является открытым множеством (почему?).

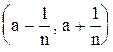
Точка а называется предельной точкой множества Х, если в любой проколотой окрестности 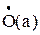этой точки имеется, по крайней мере, одна точка множества Х.

Так, точка является предельной точкой отрезка [0, 1], так как в любом проколотом интервале точки есть точка, принадлежащая этому отрезку. Например, точка , удовлетворяющая неравенству . И таких точек, очевидно, много.

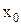
предельные точки множества могут принадлежать ему и могут не принадлежать. Можно доказать, что в любой проколотой окрестности предельной точки а множества Х имеется бесконечно много точек множества Х.

Множество Х называется замкнутым множеством, если оно содержит все свои предельные точки.

Так,всякий отрезок есть замкнутое множество. Интервал (0, 1) не является замкнутым множеством, так как ему не принадлежат две его предельные точки 0 и 1. Множество всех рациональных чисел Q не является замкнутым, так как не содержит некоторые свои предельные точки. В частности, число 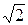является предельной точкой множества Q (докажите!), но Q.

Так как каждая точка множества R является предельной точкой этого множества и принадлежит ему, то R – замкнутое множество.

Пустое множество условимся также считать замкнутым,так как оно содержит все свои предельные точки,которых у него нет.

Всякое конечное множество является замкнутым, так как множество его предельных точек является пустым множеством Æ, которое принадлежит самому множеству.

Теорема:

1) Объединение конечного числа замкнутых множеств есть замкнутое множество;

Источник