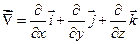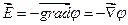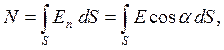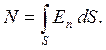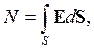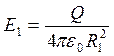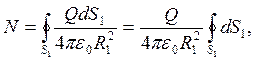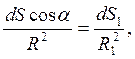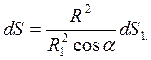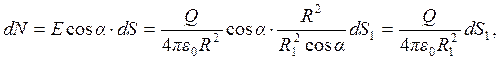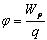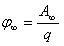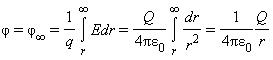доказать что силовые линии перпендикулярны эквипотенциальным поверхностям
Эквипотенциальные поверхности
Публикации по материалам Д. Джанколи. «Физика в двух томах» 1984 г. Том 2.
Эквипотенциальная поверхность в любой точке должна быть перпендикулярна направлению напряженности электрического поля. Если бы это было не так (т. е. если бы существовала компонента Е, параллельная поверхности), то для перемещения заряда вдоль поверхности в направлении, противоположном этой компоненте Е, приходилось бы совершать работу, что противоречит предположению об эквипотенциальности поверхности.
Тот факт, что силовые линии электрического поля перпендикулярны эквипотенциальным поверхностям, помогает построению эквипотенциальных поверхностей, если известно расположение силовых линий.
На рис. 24.2 изображено несколько эквипотенциальных линий (штриховые линии) для поля между параллельными пластинами, разность потенциалов которых составляет 20 В. Эти линии принадлежат эквипотенциальным поверхностям, которые пересекают рисунок перпендикулярно плоскости книжной страницы. Потенциал отрицательной пластины условно принят за нулевой; указан соответствующий потенциал каждой эквипотенциальной линии. Эквипотенциальные линии для случая двух равных по величине и противоположных по знаку зарядов показаны штриховыми линиями на рис. 24.3.
В одном из разделов ранее мы видели, что в статическом случае внутри проводника не существует электрическое поле, так как в противном случае на свободные электроны действовала бы сила и они пришли бы в движение. Иными словами, в статическом случае проводник должен находиться целиком под одним и тем же потенциалом, и поверхность проводника является, таким образом, эквипотенциальной. (Иначе свободные электроны на поверхности пришли бы в движение.) Это полностью согласуется с уже отмеченным выше фактом, что электрическое поле у поверхности проводника перпендикулярно поверхности.
Продолжение следует. Коротко о следующей публикации:
Электрон-вольт, единица энергии.
Один электрон-вольт равен энергии, которую приобретает электрон, проходя разность потенциалов 1 В.
Замечания и предложения принимаются и приветствуются!
Эквипотенциальные поверхности
Силовые линии электростатического поля
Непрерывные линии, касательные к которым в каждой точке, через которую они проходят, совпадают с вектором напряженности, называются силовыми линиями электрического поля или линиями напряженности.
В действительности силовых линий не существует, это просто графический метод исследования электростатических полей.
Силовые линии наделены следующими свойствами:
– Силовые линии электростатического поля не замкнуты ‑ они начинаются на положительных и заканчиваются на отрицательных зарядах.
– Линии непрерывны и нигде не пересекаются (т.к. их пересечение означало бы отсутствие определенного направления напряженности электрического поля в данной точке).
– Густота линий выбирается так, чтобы количество линий, пронизывающих единицу поверхности площадки, перпендикулярной к линиям, было равно численному значению (модулю) вектора 
.
 |
Так как силовые линии начинаются или оканчиваются на заряженных телах, а затем расходятся в разные стороны, то густота линий больше вблизи заряженных тел. Следовательно, вблизи заряженных тел напряженность поля больше, чем в более удалённых точках.
– Общее число силовых линий пересекающих некоторую поверхность иначе называют потоком вектора напряжённости поля.
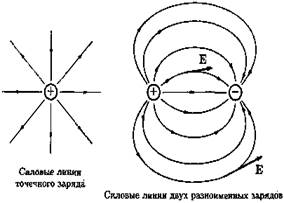
На рис. 1.4 приведены силовые линии точечных положительного и отрицательного зарядов и электрического диполя (системы двух зарядов).
С графическим изображением полей, создаваемых более сложной системы зарядов можно познакомиться в лаборатории виртуального практикума кафедры «Физика».
Для более наглядного графического изображения полей кроме линий напряжённости используют поверхности равного потенциала или эквипотенциальные поверхности. Как следует из названия, эквипотенциальная поверхность – это такая поверхность, все точки которой имеют одинаковый потенциал. Если потенциал задан как функция x, y, z, то уравнение эквипотенциальной поверхности имеет вид:
.
Линии напряжённости поля перпендикулярны эквипотенциальным поверхностям.
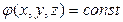
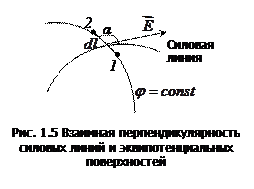
Докажем это утверждение.
Пусть линия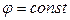 
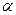
и силовая линия составляют некоторый угол 
(рис. 1.5).
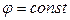
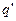
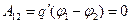
Переместим из точки 1 в точку 2 вдоль линии пробный заряд 
. При этом силы поля совершают работу:
. (1.5)
Т.е. работа перемещения пробного заряда вдоль эквипотенциальной поверхности равна нулю. Эту же работу можно определить и другим способом – как произведение заряда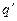 
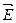
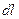
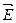
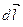
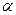
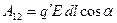
на модуль напряженности 
поля, действующего на пробный заряд, на величину перемещения 
и на косинус угла между вектором и вектором перемещения 
, т.е. косинус угла (рис. 1.5):
.
Величина работы не зависит от способа её подсчёта, согласно (1.5) она равна нулю. Отсюда вытекает, что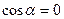 
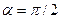
и, соответственно 
, что и требовалось доказать.
|
|
|
|
Эквипотенциальную поверхность можно провести через любую точку поля. Следовательно, таких поверхностей может быть построено бесконечное множество. Условились, однако, проводить поверхности
таким образом, чтобы разность потенциалов для двух соседних поверхностей была бы всюду одна и та же. Тогда по густоте эквипотенциальных поверхностей можно судить о величине напряжённости поля. Действительно, чем гуще располагаются эквипотенциальные поверхности, тем быстрее изменяется потенциал при перемещении вдоль нормали к поверхности.
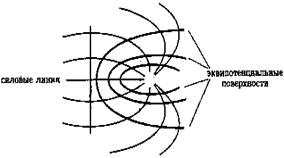
На рис. 1.6 (а) показаны эквипотенциальные поверхности (точнее, их пересечения с плоскостью чертежа) для поля точечного заряда. В соответствии с характером изменения 
эквипотенциальные поверхности при приближении к заряду становятся гуще.
На рис. 1.6 (б) изображены эквипотенциальные поверхности и линии напряжённости для поля диполя.
Из рис. 1.6 видно, что при одновременном использовании эквипотенциальных поверхностей и линий напряжённости картина поля получается особенно наглядной.
Для однородного поля эквипотенциальные поверхности, очевидно, представляют собой систему равноотстоящих друг от друга плоскостей, перпендикулярных к направлению напряжённости поля.
1.8 Связь между напряжённостью поля и потенциалом (градиент потенциала)
Пусть имеется произвольное электростатическое поле. В этом
поле проведём две эквипотенциальные поверхности таким образом, что они отличаются одна от другой потенциалом на величину dφ (рис. 1.7)
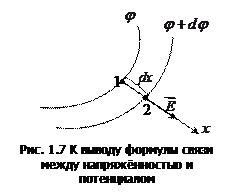
Вектор напряжённости направлен по нормали к поверхности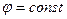 
. Направление нормали совпадает с направлением оси x.
Ось x, проведённая из точки 1, пересекает поверхность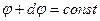 
в точке 2.
Отрезок dx представляет собой кратчайшее расстояние между точками 1 и 2. Работа, совершаемая при перемещении заряда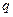 
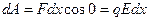
вдоль этого отрезка:
.
С другой стороны, эту же работу можно записать как:
.
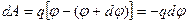
Приравнивая эти два выражения, получим:
, (1.6)
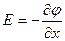
где символ частной производной подчёркивает, что дифференцирование производиться только по x. Повторив аналогичные рассуждения для осей y и z, можем найти вектор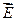 
:
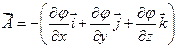
, (1.7)
где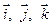 
– единичные векторы координатных осей x, y, z.
Вектор, определяемый выражением (1.7) называется градиентом скаляра φ. Для него наряду с обозначением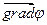 
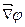
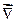
применяется также обозначение 
. 
(«набла») означает символический вектор, называемый оператором Гамильтона 
Следовательно, из определения градиента можно записать:
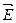
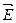
т.е. напряжённость поля равна градиенту потенциала со знаком минус. Знак минус определяется тем, что вектор напряжённости поля направлен в сторону убывания потенциала.
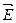
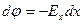
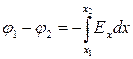
По формуле 1.7 можно найти проекцию вектора на выбранное направление в пространстве, например на ось x:
, или 
, (1.8)
где (
) − разность потенциалов между точками 1 и 2, расположенными на оси x.
Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет
1.4. Силовые линии и эквипотенциальные поверхности
Для наглядного изображения электрических полей часто рисуют силовые линии. Силовая линия — это линия, касательная к которой в каждой точке совпадает с направлением вектора напряженности в этой точке. Очевидно, что силовые линии не могут пересекаться под ненулевым углом: в противном случае в точке пересечения напряженность была бы направлена сразу в две стороны, что абсурдно. Можно легко доказать, что силовые линии не могут и касаться друг друга. В вакууме электрические силовые линии начинаются и заканчиваются либо на заряженных телах, либо в бесконечности (см. рис. 4).
Эквипотенциальной поверхностью называется такая поверхность, все точки которой обладают одним и тем же значением потенциала. Так же как и силовых линий, эквипотенциальных поверхностей может быть построено бесконечно много.
Так как все точки эквипотенциальной поверхности имеют одинаковый потенциал, перемещение заряда, по этой поверхности не требует работы (работа пропорциональна разности потенциалов). Но работа пропорциональна косинусу угла между перемещением и силой, поэтому сила, а значит и напряженность, всегда перпендикулярна к эквипотенциальной поверхности. Таким образом, эквипотенциальные поверхности всегда перпендикулярны силовым линиям (см.рис.5)
Для напряженности электрического поля выполняется теорема Гаусса. Хотя мы покажем ее на основе закона Кулона, эта теорема справедлива в самом общем случае, т. е. для электрических полей любой природы, а не только электростатических.
Вначале определим новую величину. Потоком вектора напряженности электрического поля Е через поверхность S называется величина N, равная
где En — проекция вектора Е на направление нормали к поверхности. Эту формулу можно пояснить следующим образом.
Эту формулу можно записать как
введя вектор dS = n × dS, величина которого равна площади dS, а направление совпадает с направлением единичного вектора нормали n.
Оказывается, поток вектора E через любую замкнутую поверхность определяется только суммарным зарядом, находящимся внутри нее (теорема Гаусса). Докажем ее.
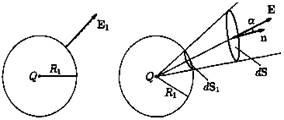
Проведем вокруг точечного заряда Q сферу радиуса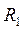
, центр которой совпадает с зарядом(см. рис. 7а). В каждой точке сферы вектор напряженности по величине равен
и направлен перпендикулярно поверхности сферы. Следовательно, поток вектора напряженности через сферу есть
где интегрирование производится по всей поверхности сферы. Очевидно, что последний интеграл — это площадь поверхности сферы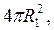 
поэтому поток через сферу равен
Пусть теперь заряд окружен произвольной поверхностью S и элемент ее dS выделяется тем же пучком линий, что и элемент первоначальной сферической поверхности (см. рис. 7б). Очевидно.
где R — расстояние от элемента поверхности dS до заряда, 
— угол между нормалью к dS и радиус-вектором R. Поэтому
Поток вектора напряженности через элемент dS равен
т. е. точно равен потоку через элемент 
. Поэтому полный поток через всю произвольную замкнутую поверхность S такой же, как и через сферическую поверхность, т. е. равен
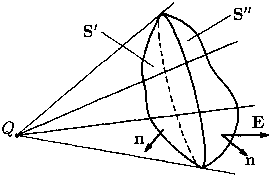
Поток вектора напряженности от точечного заряда через замкнутую поверхность равен нулю, если заряд лежит вне этой поверхности. Действительно, пучок касательных, проведенных от заряда, делит поверхность на две части — S’ и S’’ (см. рис. 8). Потоки вектора E через эти поверхности равны по величине, но имеют разные знаки, поэтому полный поток равен нулю.
Как сказал.
Вопросы к экзамену
Для всех групп технического профиля
Список лекций по физике за 1,2 семестр
Я учу детей тому, как надо учиться
Часто сталкиваюсь с тем, что дети не верят в то, что могут учиться и научиться, считают, что учиться очень трудно.
Урок 25-2. (дополнительный материал) Эквипотенциальные поверхности
Физическую величину, равную отношению потенциальной энергии электрического заряда в электростатическом поле к величине этого заряда, называют потенциалом φ электрического поля:
Во многих задачах электростатики при вычислении потенциалов за начальную точку (0) удобно принять бесконечно удаленную точку. В этом случае понятие потенциала может быть определено следующим образом:
Потенциал поля в данной точке пространства равен работе, которую совершают электрические силы при удалении единичного положительного заряда из данной точки в бесконечность.
Потенциал φ∞ поля точечного заряда Q на расстоянии r от него относительно бесконечно удаленной точки вычисляется следующим образом:
Для наглядного представления электрического поля наряду с силовыми линиями используют эквипотенциальные поверхности.
Поверхность, во всех точках которой потенциал электрического поля имеет одинаковые значения, называется эквипотенциальной поверхностью или поверхностью равного потенциала.
Силовые линии электрического поля всегда перпендикулярны эквипотенциальным поверхностям.
Эквипотенциальные поверхности кулоновского поля точечного заряда – концентрические сферы. На рисунке представлены картины силовых линий и эквипотенциальных поверхностей некоторых простых электростатических полей.
Эквипотенциальные поверхности (синие линии) и силовые линии (красные линии) простых электрических полей
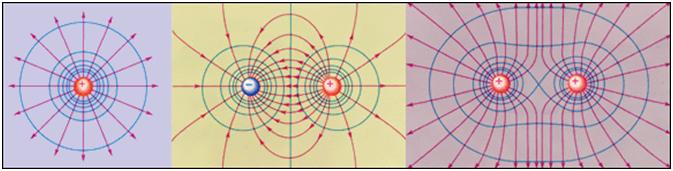
В случае однородного поля эквипотенциальные поверхности представляют собой систему параллельных плоскостей.
Свойства эквипотенциальных поверхностей:
Почему линии напряженности и эквипотенциальные поверхности перпендикулярны. Эквипотенциальные поверхности и силовые линии электростатического поля
Почему линии напряженности и эквипотенциальные поверхности перпендикулярны. Эквипотенциальные поверхности и силовые линии электростатического поля
Именно вдоль силовой линии происходит максимальное изменение потенциала. Поэтому всегда можно определитьмежду двумя точками, измеряя U между ними, причем тем точнее, чем ближе точки. В однородном электрическом поле силовые линии – прямые. Поэтому здесь определить наиболее просто:
Графическое изображение силовых линий и эквипотенциальных поверхностей показано на рисунке 3.4.
При перемещении по этой поверхности на dl потенциал не изменится:
Отсюда следует, что проекция вектора на dl равнанулю, то есть Следовательно, в каждой точке направлена по нормали к эквипотенциальной поверхности.
Формула выражает связь потенциала с напряженностью и позволяет по известным значениям φ найти напряженность поля в каждой точке. Можно решить и обратную задачу, т.е. по известным значениям в каждой точке поля найти разность потенциаловмежду двумя произвольными точками поля. Для этого воспользуемся тем, что работа, совершаемая силами поля над зарядом q при перемещении его из точки 1 в точку 2, может быть, вычислена как:
С другой стороны работу можно представить в виде:
, тогда 
Интеграл можно брать по любой линии, соединяющие точку 1 и точку 2, ибо работа сил поля не зависит от пути. Для обхода по замкнутому контуру получим:
т.е. пришли к известной нам теореме о циркуляции вектора напряженности: циркуляция вектора напряженности электростатического поля вдоль любого замкнутого контура равна нулю.
Поле, обладающее этим свойством, называется потенциальным.
Из обращения в нуль циркуляции вектора следует, что линии электростатического поля не могут быть замкнутыми:они начинаются на положительных зарядах (истоки) и на отрицательных зарядах заканчиваются (стоки) или уходят в бесконечность (рис. 3.4).
Это соотношение верно только для электростатического поля. Впоследствии мы с вами выясним, что поле движущихся зарядов не является потенциальным, и для него это соотношение не выполняется.
Связь между напряженностью и потенциалом.
Для потенциального поля, между потенциальной (консервативной) силой и потенциальной энергией существует связь
Поскольку 
то
Знак минус показывает, что вектор Е направлен в сторону убывания потенциала.
Можно показать, что во всех случаях вектор Е перпендикулярен эквипотенциальным поверхностям и всегда направлен в сторону убывания потенциала.
Примеры расчета наиболее важных симметричных электростатических полей в вакууме.
1. Электростатическое поле электрического диполя в вакууме.
Из предыдущего примера следует, что векторы напряженности Е 1 и E 2 первой и второй плоскостей равны по модулю и всюду направлены перпендикулярно плоскостям. Поэтому в пространстве вне плоскостей они компенсируют друг друга, а в пространстве между плоскостями суммарная напряженность 
. Поэтому между плоскостями
Поле между плоскостями однородное. Разность потенциалов между плоскостями.
(в диэлектрике 
).
4.Поле равномерно заряженной сферической поверхности.
Сферическая поверхность радиуса R с общим зарядом q заряжена равномерно с поверхностной плотностью 
Поскольку система зарядов и, следовательно, само поле центрально-симметрично относительно центра сферы, то линии напряженности направлены радиально.
Вне заряженной сферы поле такое же, как поле точечного заряда q, находящегося в центре сферы. Внутри заряженной сферы поля нет, поэтому потенциал всюду одинаков и такой же, как на поверхности
Графическое изображение полей, можно составить не только с линиями напряженности, но и с помощью разности потенциалов. Если объединить в электрическом поле точки с равными потенциалами, то мы получим поверхности равного потенциала или как еще их называют эквипотенциальные поверхности. В пересечении с плоскостью чертежа эквипотенциальные поверхности дают эквипотенциальные линии. Изображая эквипотенциальные линии, которые соответствуют различным значениям потенциала, мы получаем наглядную картину, которая отражает, как изменяется потенциал конкретного поля. Перемещение вдоль эквипотенциальной поверхности заряда работы не требует, так как все точки поля по такой поверхности имеют равный потенциал и сила, которая действует на заряд, всегда перпендикулярна перемещению.
Следовательно, линии напряженности всегда перпендикулярны поверхностям с равными потенциалами.
Наиболее наглядная картина поля будет представлена, если изображать эквипотенциальные линии с равными изменениями потенциала, например в 10 В, 20В, 30 В и т.д. В таком случае скорость изменения потенциала будет обратно пропорциональна расстоянию между соседними эквипотенциальными линиями. То есть густота эквипотенциальных линий пропорциональна напряженности поля (чем выше напряженность поля, тем теснее изображаются линии). Зная эквипотенциальные линии, можно построить линии напряженности рассматриваемого поля и наоборот.
Следовательно, изображения полей с помощью эквипотенциальных линий и линий напряженности равнозначны.
Нумерация эквипотенциальных линий на чертеже
Довольно часто эквипотенциальные линии на чертеже нумеруют. Для того, чтобы указать разность потенциалов на чертеже, произвольную линию обозначают цифрой 0, возле всех остальных линий расставляют цифры 1,2,3 и т.д. Эти цифры указывают разность потенциалов в вольтах избранной эквипотенциальной линии и линии, которую выбрали нулевой. При этом отмечаем, что выбор нулевой линии не важен, так как физический смысл имеет только разность потенциалов для двух поверхностей, и она не зависит от выбора нуля.
Поле точечного заряда с положительным зарядом
Что очевидно из формулы, которая определяет потенциал поля точечного заряда при нормировке потенциала на бесконечность ($\varphi \left(\infty \right)=0$):
Система параллельных плоскостей, которые находятся на равных расстояниях друг от друга, является эквипотенциальными поверхностями однородного электрического поля.
Задание: Потенциал поля, создаваемый системой зарядов, имеет вид:
Запишем уравнение (1.1) в каноническом виде:
Задание: Потенциал поля, имеет вид:
Перепишем уравнение (1.1) в виде:
Мы получили каноническое уравнение двуполостного гиперболоида, его полуоси:
Перепишем уравнение (2.5) в виде:
Электростатическое поле можно охарактеризовать совокупностью силовых и эквипотенциальных линий.
Силовая линия – это мысленно проведенная в поле линия, начинающаяся на положительно заряженном теле и заканчивающаяся на отрицательно заряженном теле, проведенная таким образом, что касательная к ней в любой точке поля дает направление напряженности в этой точке.
Силовые линии замыкаются на положительных и отрицательных зарядах и не могут замыкаться сами на себя.
Под эквипотенциальной поверхностью понимают совокупность точек поля, имеющих один и тот же потенциал ().
Если рассечь электростатическое поле секущей плоскостью, то в сечении будут видны следы пересечения плоскости с эквипотенциальными поверхностями. Эти следы называют эквипотенциальными линиями.
Эквипотенциальные линии являются замкнутыми сами на себя.
Силовые линии и эквипотенциальные линии пересекаются под прямым углом.
Р
ассмотрим эквипотенциальную поверхность:
(так как точки лежат на эквипотенциальной поверхности).
– скалярное произведение
Уравнение эквипотенциальной линии
Рассмотрим силовую линию:
Н
апряженность электростатического поля направлена по касательной к силовой линии (см. определение силовой линии), также направлен и элемент пути
, поэтому угол между этими двумя векторами равен нулю.
или 
Уравнение силовой линии
Градиент потенциала
Градиент потенциала – это скорость возрастания потенциала в направлении кротчайшем между двумя точками.
Между двумя точками имеется некоторая разность потенциалов. Если эту разность разделить на кратчайшее расстояние между взятыми точками, то полученное значение будет характеризовать скорость изменения потенциала в направлении кратчайшего расстояния между точками.
Градиент потенциала показывает направление наибольшего возрастания потенциала, численно равен модулю напряженности и отрицательно направлен по отношению к нему.
В определении градиента существенны два положения:
Направление, в котором берутся две близлежащие точки, должно быть таким, чтобы скорость изменения была максимальной.
Направление таково, что скалярная функция в этом направлении возрастает.
Для декартовой системы координат:
Скорость изменения потенциала в направлении оси Х, Y, Z:
; 
;
; 
;
.
В цилиндрической системе координат выражение градиента потенциала будет иметь следующий вид.
где символ частной производной подчеркивает, что дифференцирование производится только по х. Повторив аналогичные рассуждения для осей y и z, можем найти вектор Е:
Из определения градиента (12.4) и (12.6). следует, что
т. е. напряженность Е поля равна градиенту потенциала со знаком минус. Знак минус определяется тем, что вектор напряженности Е поля направлен в сторону убывания потенциала.
Если поле создается точечным зарядом, то его потенциал, согласно (84.5),
Линии напряженности всегда нормальны к эквипотенциальным поверхностям. Действительно, все точки эквипотенциальной поверхности имеют одинаковый потенциал, поэтому работа по перемещению заряда вдоль этой поверхности равна нулю, т. е. электростатические силы, действующие на заряд, всегда направлены по нормалям к эквипотенциальным поверхностям. Следовательно, вектор Е всегда нормален к эквипотенциальным поверхностям, а поэтому линии вектора Е ортогональны этим поверхностям.
Эквипотенциальных поверхностей вокруг каждого заряда и каждой системы зарядов можно провести бесчисленное множество. Однако их обычно проводят так, чтобы разности потенциалов между любыми двумя соседними эквипотенциальными поверхностями были одинаковы. Тогда густота эквипотенциальных поверхностей наглядно характеризует напряженность поля в разных точках. Там, где эти поверхности рас положены гуще, напряженность поля больше.