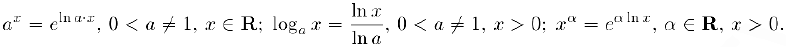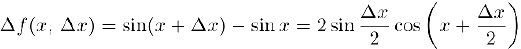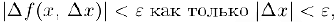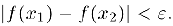доказать что синус непрерывная функция

Как доказать непрерывность функции

Пример 1: докажите непрерывность функции f(x) = x^2 в точке x_0.

По ε-Δ определению существует такое ε > 0, что |x^2 – x_0^2|

Некоторые элементарные функции являются непрерывными на всей области определения (множестве значений X):

Пример 2: докажите непрерывность функции f(x) = sin x.

По определению непрерывности функции по ее бесконечно малому приращению запишите:

Преобразуйте по формуле для тригонометрических функций:

Δf = 2*cos((x + Δx)/2)*sin(Δx/2).

Функция cos ограничена при x ≤ 0, а предел функции sin(Δx/2) стремится к нулю, следовательно, она является бесконечно малой при Δx→0. Произведение ограниченной функции и бесконечно малоq величины, а значит и приращение исходной функции Δf также является бесконечной малой величиной. Следовательно, функция f(x) = sin x непрерывна для любого значения x.

Пример 1: докажите непрерывность функции f(x) = x^2 в точке x_0.

По ε-Δ определению существует такое ε > 0, что |x^2 – x_0^2|

Некоторые элементарные функции являются непрерывными на всей области определения (множестве значений X):

Пример 2: докажите непрерывность функции f(x) = sin x.

По определению непрерывности функции по ее бесконечно малому приращению запишите:

Преобразуйте по формуле для тригонометрических функций:

Δf = 2*cos((x + Δx)/2)*sin(Δx/2).

Функция cos ограничена при x ≤ 0, а предел функции sin(Δx/2) стремится к нулю, следовательно, она является бесконечно малой при Δx→0. Произведение ограниченной функции и бесконечно малоq величины, а значит и приращение исходной функции Δf также является бесконечной малой величиной. Следовательно, функция f(x) = sin x непрерывна для любого значения x.

Некоторые элементарные функции являются непрерывными на всей области определения (множестве значений X):

Пример 2: докажите непрерывность функции f(x) = sin x.

По определению непрерывности функции по ее бесконечно малому приращению запишите:

Преобразуйте по формуле для тригонометрических функций:

Δf = 2*cos((x + Δx)/2)*sin(Δx/2).

Функция cos ограничена при x ≤ 0, а предел функции sin(Δx/2) стремится к нулю, следовательно, она является бесконечно малой при Δx→0. Произведение ограниченной функции и бесконечно малоq величины, а значит и приращение исходной функции Δf также является бесконечной малой величиной. Следовательно, функция f(x) = sin x непрерывна для любого значения x.

Источник

Непрерывность элементарных функций

Непрерывность элементарных функций

Докажем, что любая элементарная функция непрерывна всюду, где она определена. Как следует из общих свойств непрерывности (пункт 1) для этого достаточно доказать, что непрерывными в своей области определения являются основные элементарные функции.

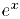
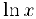
Непрерывность экспоненты и натурального логарифма (равенства (1)). Отсюда на основании свойств 1), 2) непрерывности (пункт 1) немедленно следует непрерывность функций

Осталось доказать непрерывность тригонометрических и обратных тригонометрических функций. Рассмотрим приращение функции 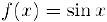в произвольной точке x:

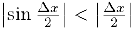
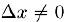
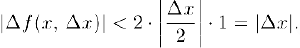
Из неравенства (1), §4, пункт 3 следует, что при малых . поэтому, .

Отсюда мы заключаем, что при любом заданном

т. е. 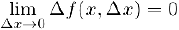. что и означает непрерывность функции sin x.

Непрерывность остальных тригонометрических функций следует из соотношений

и уже упоминавшихся общих свойств непрерывности (пункт 1).

Для доказательства непрерывности обратных тригонометрических функций достаточно сослаться на теорему о непрерывности обратной функции из предыдущего пункта.

Равномерная непрерывность функции

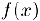
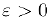
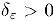
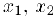
Определение. Функция называется равномерно непрерывной на некотором промежутке числовой оси (конечном, или бесконечном), если она определена на этом промежутке и для любого положительного числа найдется положительное число , обладающее тем свойством, что при всех из данного промежутка, удовлетворяющих неравенству

для соответствующих значений функции выполняется неравенство

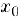
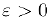
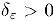
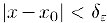
Покажем что равномерная непрерывность является более, сильным свойством функции, чем ее непрерывность на промежутке. Действительно, если функция равномерно непрерывна па некотором промежутке, то, зафиксировав произвольную точку , этого промежутка, мы получим, что для любого отыщется такое, что как только , что и означает непрерывность функции на данном промежутке. Убедимся теперь на примере в том. что из непрерывности функции на промежутке еще не следует, вообще говоря, равномерная непрерывность.

Эта лекция взята со страницы онлайн помощи по математическому анализу:

Возможно эти страницы вам будут полезны:

Образовательный сайт для студентов и школьников

Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.

© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института

Источник

Непрерывность элементарных функций

Многочлены и рациональные функции.

Рассмотрим многочлен степени \(n\), то есть функцию вида
$$
P_(x)=a_x^+a_x^+\ +a_<1>x+a_<0>,\; a_\neq 0.\nonumber
$$
Эта функция непрерывна на \(\mathbb\).

\(\circ\) Действительно, функция \(y=C\), где \(C\) — постоянная, непрерывна на \(\mathbb\), так как \(\Delta y=0\) при любом \(x\). Функция \(y=x\) непрерывна на \(\mathbb\), так как \(\Delta y=\Delta x\rightarrow 0\) при \(\Delta x\rightarrow 0\). Поэтому функция \(y=a_x^k\), где \(k\in\mathbb\), непрерывна на \(\mathbb\) как произведение непрерывных Функций. Так как многочлен \(P_(x)\) есть сумма непрерывных функций вида \(a_x_k\;(k=\overline<0,n>)\), то он непрерывен на \(\mathbb\). \(\bullet\)

Рациональная функция, то есть функция вида \(f(x)=\displaystyle \frac\), где \(P_,\;Q_\) — многочлены степени n и m соответственно, непрерывна во всех точках, которые не являются нулями многочлена \(Q_(x)\).

В самом деле, если \(Q_m(x)\neq 0\), то из непрерывности многочленов \(P_\) и \(Q_\) следует непрерывность функции \(f\) в точке \(x\). \(\bullet\)

Тригонометрические и обратные тригонометрические функции.

Неравенства для тригонометрических функций.

Если \(\displaystyle x\in\left(-\frac<\mathrm\pi>2,\frac<\mathrm\pi>2\right)\) и \(x\neq 0\), то
$$
\cos x Доказательство

\(\circ\) Рассмотрим в координатной плоскости круг единичного радиуса с центром в точке \(O\) (рис. 12.1). Пусть \(\angle=x\) где \(0 Рис. 12.1

Пусть \(S_<1>,\;S_<2>,\;S_<3>\) — площади треугольника AOB, сектора AOB и треугольника AOD соответственно. Тогда \(S_<1>=\displaystyle \frac<1><2>(OA)^2\sin x=\frac<1><2>\sin x\), \(\displaystyle S_<2>=\frac<1><2>(OA)^<2>x=\frac<1><2>x\), \(S_<3>=\displaystyle\frac<1><2>OA\cdot DA=\frac<1><2>\tan x\). Так как \(S_ <1>0\), и поэтому неравенство \eqref равносильно неравенству
$$
1 Замечание 1

Из неравенства \eqref следует, что
$$
\tan x>x\ \mbox<при>\ x\in(0,\frac<\pi><2>).\label
$$

Для всех \(x\in\mathbb\) справедливо неравенство
$$
\left|\sin x\right|\leq\left|x\right|\label
$$

\(\circ\) Неравенство \eqref выполняется при \(x=0\). Пусть \(x\neq 0\). Тогда если \(\displaystyle x\in\left(0,\frac<\pi>2\right)\), то из \eqref следует неравенство \(\displaystyle \frac<\sin x> 1\). \(\bullet\)

Непрерывность тригонометрических функций.

Функции \(y=\sin x\) и \(y=\cos x\) непрерывны на \(\mathbb\).

\(\circ\) Пусть \(x_0\) — произвольная точка множества \(\mathbb\). Тогда \(\sin x-\sin x_<0>=\displaystyle 2\sin\frac><2>\cos\frac><2>\). Так как \(\displaystyle\left|\sin\frac><2>\right|\leq\left|\frac><2>\right|\) в силу неравенства \eqref, а \(\displaystyle\left|\cos \frac><2>\right|\leq 1\), то \(\left|\sin x — \sin x_0\right|\leq|x-x_0|\), откуда следует, что функция \(y=\sin x\) непрерывна в точке \(x_0\).

Аналогично имеем
$$
\cos x-\cos x_<0>=2\sin\frac><2>\sin\frac-x><2>,\nonumber
$$
откуда \(|\cos x-\cos x_<0>| Утверждение 6

\(\circ\) Воспользуемся неравенством \eqref. В силу непрерывности косинуса \(\displaystyle \lim_\cos x=\cos 0=1\). Переходя в соотношении \eqref к пределу при \(x\rightarrow 0\), получаем равенство \eqref. \(\bullet\)

Обратные тригонометрические функции.

\(\sin x\) и \(\arcsin x\).

Рассмотрим функцию
$$
y=\sin x,\quad x\in\left[-\frac<\pi><2>,\frac<\pi><2>\right]=\Delta.\label
$$

Эта функция, график которой изображен на рис. 12.2, непрерывна и строго возрастает на отрезке \(\Delta\), множество ее значений — отрезок [-1, 1]. По теореме об обратной функции на отрезке [-1,1] определена функция, обратная к функции \eqref, непрерывная и строго возрастающая. Ее обозначают
$$
y=\arcsin x,\quad x\in[-1,1].\nonumber
$$

Рис. 12.2 Рис. 12.3

Подчеркнем, что функция \(\arcsin x\) не является обратной к периодической функции \(\sin x\), которая необратима; \(\arcsin x\) — функция, обратная по отношению к функции \(\sin x\) заданной на отрезке \(\Delta=\left[-\displaystyle \frac<\pi><2>,\frac<\pi><2>\right]\), то есть обратная к сужению \(\sin x\) на отрезок \(\Delta\). График функции \(y=\arcsin x\), изображенный на рис 12.3, симметричен графику функции \eqref относительно прямой \(y=x\). В силу свойств взаимно обратных функций
\begin
\sin(\arcsin x)=x,\quad x\in[-1,1]\nonumber\\
\arcsin(\sin x)=x,\quad x\in\left[-\frac<\pi><2>,\frac<\pi><2>\right]\label\\
\arcsin(-x)=-\arcsin x,\quad x\in [-1,1]\label
\end
то есть \(\arcsin x\) — нечетная функция.

Построить график функции \(y=\arcsin(\sin x)\).

\(\triangle\) Функция определена на \(\mathbb\) и является периодической с периодом \(2\pi\). Поэтому достаточно построить ее график на отрезке \(\displaystyle\left[-\frac<\pi>2,\frac<3\pi>2\right]\).

Рис. 12.4

\(\cos x\) и \(\arccos x\).

Функция
$$
y=\cos x,\quad 0\leq x\leq\pi,\nonumber
$$
непрерывна и строго убывает. Обратная к ней функция, которую обозначают
$$
у=\arccos x, x\in[-1,1],\nonumber
$$
непрерывна и строго убывает. График этой функции изображен на рис. 12.5. По свойствам взаимно обратных функций
\begin
\cos(\arccos x)=x,\quad x\in[-1,1],\nonumber\\
\arccos(\cos x)=x,\quad x\in[0,\pi].\nonumber
\end

Рис. 12.5

\(\operatorname x\) и \(\operatorname x\).

Функция
$$
y=\tan x,\quad-\frac<\pi> <2> Рис. 12.6

Отметим, что в силу свойств взаимно обратных функций имеем
\begin
\tan(\arctan x)=x,\quad x\in\mathbb,\nonumber\\
\arctan(\tan x)=x,\quad x\in\left(-\frac<\pi>2,\frac<\pi>2\right)\nonumber\\
\arctan(-x)=-\arctan x,\quad x\in\mathbb,\nonumber
\end

\(\operatorname x\) и \(\operatorname x\).

Функцию, обратную к функции
$$
y=\operatornamex,\quad 0 Рис. 12.7

Степенная функция с рациональным показателем.

Степенная функция с натуральным показателем, то есть
$$
y=x^n,\quad x\in\mathbb,\nonumber
$$
где \(n\in\mathbb\), непрерывна на \(\mathbb\). Если \(n=2k+1\), то эта функция строго возрастает на \(\mathbb\) и поэтому обратима. На рис. 12.8 изображены графики функций \(y=x^3\) и \(y=\displaystyle \sqrt[3]=x^<1>\).

Рис. 12.8

Степенная функция с четным натуральным показателем, то есть функция \(y=x^<2k>,\;k\in\mathbb,\;x\in\mathbb\), необратима. Однако ее сужение на множество \([0,+\infty)\), то есть функция \(y=x^<2k>,\ k\in\mathbb\ x\in [0,+\infty)\), обратима и обратной к ней является функция \(y=\displaystyle \sqrt[2k]\). На рис. 12.81 изображены графики взаимно обратных функций \(y=x^2,\;x\in [0,+\infty)\), и \(y=\sqrt\).

Рис. 12.81

Рис. 12.82

Если \(x>0\), то при любом \(n\in\mathbb\) функция \(x^n\) обратима, а обратная к ней функция обозначается \(x^<1>\) или \(\sqrt[n]\). Функция \(y=x^<-n>,\;n\in\mathbb\), определена и непрерывна при \(x\neq 0\) и записывается в виде \(y=1/x^\). При \(n=2k+1\;(k\in\mathbb)\) эта функция обратима на множестве \(E=\,\; x\neq 0\>\), а при \(n=2k\;(k\in\mathbb)\) обратима на множествах \((-\infty,0)\) и \((0,+\infty)\).

Рис. 12.9

Дадим определение степенной функции \(x^r\) с рациональным показателем \(r\). Если \(r=m/n,\;m\in\mathbb,\;n\in\mathbb\), то положим
$$
x^r=\left(x^<1>\right)^m,\quad x>0.\label
$$

Функция \(x^<1>\) непрерывна и строго возрастает (рис. 12.9).

Функция \(t^m\) непрерывна при \(t>0\), строго возрастает, если \(m>0\), и строго убывает, если \(m\; 0\), строго возрастает, если \(r>0\), и строго убывает, если \(r\; 0,\label\\
a^r>1,\;при\;r\in\mathbb,\;a>1,\;r>0,\label\\
a^a^=a^,\;при\;a>0,\;r_1\in\mathbb,\;r_2\in\mathbb\label\\
(a^)^=a^,\;при\;a>0,\;r_1\in\mathbb,\;r_2\in\mathbb\label\\
a^>a^,\;при\;a>1,\;r_1\in\mathbb,\;r_2\in\mathbb,\;r_1>r_2.\label
\end

Свойства \eqref-\eqref легко проверяются, если воспользоваться свойствами целых степеней и тем, что при \(a>0,\;b>0\) из \(a^n=b^n,\;n\in\mathbb\), следует \(а=b\). Проверим, например, равенство \eqref.

Показательная функция.

Свойства функции \(a^r\), где \(a>1,\ r\in\mathbb\).

Если \(a > 1\), то
$$
\forall\varepsilon>0\;\exists\delta>0:\;\forall r\in\mathbb:\;|r|\; Доказательство

\(\circ\) Мы уже доказывали, что если \(a>1\), то
$$
\lim_a^<1>=1.\label
$$
Отсюда следует, что
$$
\lim_ a^<-1/n>=1.\label
$$
Заметим, что соотношения \eqref и \eqref справедливы и в случае, когда \(0\; 1\), то
$$
\forall\epsilon>0\ \exists p\in\mathbb:\ 0 1\) (неравенство \eqref) получаем
$$
a^ <-1/p>0\) существует число \(\delta=1/p>0\) такое, что для всех рациональных чисел \(r\), удовлетворяющих условию \(|r| Утверждение 8

Если последовательность рациональных чисел \(\\>\) сходится, то последовательность \(\>\>\), где \(a>1\), также сходится

\(\circ\) Из сходимости последовательности \(\\>\) следует ее ограниченность, то есть
$$
\exists\alpha,\;\beta :\;\forall n\in\mathbb\rightarrow\alpha\leq r_n\leq\beta,\;\alpha\in\mathbb,\;\beta\in\mathbb,\nonumber
$$
Откуда в силу \eqref получаем
$$
a^<\alpha>\leq a^>\leq a^<\beta>.\nonumber
$$
Учитывая, что \(a^<\alpha>>0\), и обозначая \(C=\alpha^\beta\), находим, что
$$
\exists C>0:\;\forall n\in\mathbb\rightarrow 0\; 0\;\exists \delta>0:\;\forall r\in\mathbb:\;|r| 0\) можно подобрать номер
$$
N_:\ \forall n\geq N_<\varepsilon>,\ \forall m\geq N_<\varepsilon>\rightarrow|r_n-r_m| 0\ \exists N_<\varepsilon>:\ \forall n\geq N_<\varepsilon>,\ \forall m\geq N_<\varepsilon>\rightarrow|a^>-a^>| Определение

Пусть \(x\) — произвольная точка числовой прямой, и пусть \(\\) — последовательность рациональных чисел, сходящихся к \(x\), то есть \(\displaystyle \lim_r_n=x\). Предполагая, что \(a>0\), положим по определению
$$
a^x=\lim_a^.\label
$$

Если \(a>1\), то предел \eqref существует в силу утверждения 8. Если \(0 1\), откуда следует, что существует предел \eqref и при \(a\in (0,1)\), так как \(\displaystyle\lim_b^>=b^x>0\) (смотри доказанное ниже неравенство \eqref). При \(a=1\) предел \eqref существует и равен 1, так как \(1^r=1\) для любого \(r\in\mathbb\). Заметим, что определение показательной функции является корректным, то есть предел \eqref не зависит от выбора последовательности рациональных чисел, сходящихся к \(x\) в силу ранее доказанной леммы.

Свойства функции \(y=a^x,\ a>1\).

Для любых вещественных чисел \(x_<1>\) и \(x_<2>\) выполняется равенство
$$
a^>a^>=a^+x_<2>>.\label
$$

Так как в силу равенства \eqref \(a^+\rho_>=a^>a^<\rho_>\), то, переходя в последнем равенстве к пределу при \(n\rightarrow\infty\), получаем равенство \eqref. \(\bullet\)

Из этой формулы, в частности, следует, что для любого \(x\in\mathbb\) выполняется равенство
$$
a^<-x>=\frac<1>>.\label
$$

Функция \(y=a^x\), где \(a>1\), строго возрастает на \(\mathbb\).

\(\circ\) Нужно доказать, что
$$
\forall x_<1>\in\mathbb,\;\forall x_<2>\in\mathbb:\ x_ <1>0.\label
$$

В самом деле, пусть \(r\in\mathbb\) и \(r r\) при \(n\in\mathbb\). Тогда \(a^>>a^r\) в силу \eqref, откуда, переходя к пределу, получаем \( a^\geq a^\), где \(a>0\). Итак, \(a\geq a^r>0\), то есть выполняется неравенство \eqref. Чтобы доказать неравенство \eqref, умножим обе части его на \(a^<-x_<1>>>0\) и, пользуясь свойством 1, получим неравенство
$$
a^-x_<1>>>1,\ x_<2>>x_<1>,\nonumber
$$
равносильное неравенству \eqref. Полагая \(x_<2>-x_<1>=x\), получим неравенство
$$
a^x>1,\ если\ x>0.\label
$$
Итак, для доказательства утверждения \eqref достаточно доказать равносильное ему утверждение \eqref.

Пусть \(r\in\mathbb\) таково, что \(0 r\) для \(n\in\mathbb\). Тогда, используя неравенства \eqref и \eqref, имеем \(a^>>a^>1\), откуда, переходя к пределу при \(n\rightarrow\infty\), получаем \(a^\geq a^>1\). Свойство 2 доказано. \(\bullet\)

Функция \(y=a^x\), где \(a\;>\;1\), непрерывна на \(\mathbb\).

\(\circ\) Пусть \(x_0\) — произвольная точка множества \(\mathbb,\;\Delta y=a^+\Delta x>-a^=a^(a^<\Delta x>-1)\). Нужно доказать, что \(a^<\Delta x>\rightarrow 1\) при \(\Delta x\rightarrow 0\) или
$$
\lim_a^x=1.\label
$$
Пусть \(\\>\) произвольная последовательность вещественных чисел такая, что \(\displaystyle \lim_x_n=0\). В силу свойств вещественных чисел найдутся последовательности рациональных чисел \(\\) и \(\’\>\), удовлетворяющие при \(n\in\mathbb\) условию
$$
x_-\frac<1> Свойство 4

Для любого \(x_1\in\mathbb\) и любого \(x_2\in\mathbb\) справедливо равенство
$$
(a^>)^>=a^x_<2>>.\label
$$

\(\circ\) Из неравенства \(x\geq[x]\) в силу свойства 2 получаем \(a^\geq a^<[x]>\). Так как \(а>1\), то \(a=1+\alpha\), где \(\alpha>0\). Применяя неравенство Бернулли, имеем
$$
a^<[x]>=(1+\alpha)^<[x]>>\alpha[x]>\alpha(x-1).\nonumber
$$
Итак, \(a^>\alpha(x-1\), где \(\alpha>0\), откуда следует соотношение \eqref. Если \(x\; 1\), непрерывна на всей числовой оси и строго возрастает; множество ее значений — интервал \((0,+\infty)\).

Свойство 1, свойство 3, свойство 4 остаются в силе и для показательной функции \(y=a^x\), где \(0 1\), которая является строго возрастающей, функция \(y=a^x,\ 0 1\) и \(0 Рис. 12.10 Рис. 12.11

В качестве основания показательной функции часто используют число \(e\), а функцию \(y=e^\) называют экспоненциальной и обозначают \(\exp x\).

Построить график функции \(y=e^<1>\).

\(\triangle\) Функция \(e^<1>\) — определена при \(x\neq 0\), принимает положительные значения при всех \(x\neq 0\), является строго убывающей на интервалах \(E_1=(-\infty,0)\) и \(E_2=(0,+\infty)\), причем \(e^ <1>1\) при \(x\in E_2\). Учитывая, что \(\displaystyle \lim_e^<1>=1-0\), \(\displaystyle\lim_e^<1>=+0\), \(\displaystyle\lim_e^<1>=+\infty\), \(\displaystyle\lim_e^<1>=1+0\), строим график функции \(y=e^<1>\) (рис. 12.12). \(\blacktriangle\)

Логарифмическая функция.

Рис. 12.13 Рис. 12.14

Гиперболические функции и обратные к ним.

Функции, заданные формулами
$$
\operatornamex=\frac+e^<-x>><2>,\quad \operatornamex=\frac-e^<-x>><2>,\nonumber
$$
называют соответственно гиперболическим косинусом и гиперболическим синусом.

Эти функции определены и непрерывны на \(\mathbb\), причем \(\operatorname\) — четная функция, a \(\operatorname\) — нечетная функция. Графики функций \(y=\operatornamex\) и \(y=\operatornamex\) изображены на рис. 12.15.

Из определения гиперболических функций \(\operatorname\) и \(\operatorname\) следует, что
\begin
\operatornamex+\operatornamex=e^,\quad \operatorname^<2>x-\operatorname^<2>x=1,\label\\
\operatorname2x=1+2\operatorname^<2>x,\quad\operatorname2x=2\operatornamex\operatornamex.\label
\end

По аналогии с тригонометрическими функциями гиперболические тангенс и котангенс определяются соответственно формулами
$$
\operatorname

x=\displaystyle \frac<\operatornamex><\operatornamex>,\quad \operatornamex=\displaystyle \frac<\operatornamex><\operatornamex>.\nonumber
$$

Рис. 12.16 Рис. 12.17

Функция \(\operatorname

x\) определена и непрерывна на \(\mathbb\), а функция \(\operatorname\) — определена и непрерывна на множестве \(\mathbb\) с выколотой точкой \(x=0\); обе функции нечетные, их графики представлены на рис. 12.16 и рис. 12.17.

Можно показать (в дальнейшем мы разберем этот пример, используя производные), что функции \(y=\operatornamex,\;y=\operatorname

X\) и \(y=\operatorname<сh>x,\;x>0\), строго возрастающие, а функция \(\operatornamex,\;x\leq 0\), строго убывающая. Поэтому указанные функции обратимы. Обозначим обратные к ним функции соответственно через \(\operatornamex,\;\operatornamex,\;\operatorname_<+>x,\;\operatorname_<->x\).

Рассмотрим функцию, обратную к функции \(\operatornamex\), то есть функцию \(\operatornamex\) (читается ареа-синус от \(x\)). Выразим ее через элементарные.
Решая уравнение \(\displaystyle \operatornamex=\frac><2>=y\) относительно \(x\), получаем \(e^=y\pm\sqrt<1+y^<2>>\). Так как \(e^>0\), то \(e^=y+\sqrt<1+y^<2>>\), откуда \(x=\displaystyle \ln(y+\sqrt<1+y^<2>>)\). Если мы заменим \(x\) на \(y\), a \(y\) на \(x\), то найдем формулу для функции, обратной для гиперболического синуса:
$$
\operatorname<агsh>x=\ln(x+\sqrt<1+x^<2>>),\quad x\in\mathbb.\nonumber
$$

Название «гиперболические функции» объясняется тем, что уравнения \(x=\operatornamet,\ y=\operatornamet\) можно рассматривать как параметрические уравнения гиперболы \(x^<2>-y^<2>=1\) (см. формулу \eqref). Параметр \(t\) в уравнениях гипербол равен удвоенной площади гиперболического сектора. Это отражено в обозначениях и названиях обратных гиперболических Функций, где частица \(arc\) есть сокращение латинского (и английского) слова агеа — площадь.

Степенная функция с любым вещественным показателем.

Выше нами была рассмотрена степенная функция вида \(x^r\), где \(r\in\mathbb\) (то есть \(r\) — рациональное число). Степенная функция с любым вещественным показателем \(\alpha\) при \(x>0\) выражается формулой
$$
x^<\alpha>=e^<\alpha\ln x>.\label
$$
Функция \(x^<\alpha>\) непрерывна при \(x>0\) как суперпозиция показательной функции \(e^\) и функции \(t=\alpha\ln\), которые являются непрерывными. Из равенства \eqref и свойств показательной и логарифмической функций следует, что функция \(x^\alpha\) строго возрастает при \(\alpha>0\) и строго убывает при \(\alpha 0.\nonumber
$$

Если \(\alpha\in\mathbb\), то функция \(x^<\alpha>\) может иметь смысл при \(x

Показательно-степенная функция.

Пусть функции \(u(x)\) и \(v(x)\) определены на промежутке \(\Delta=(a,b)\), причем для всех \(x\in\Delta\) выполняется условие \(u(x)>0\). Тогда функцию \(y\), определяемую формулой
$$
y=e^>,\nonumber
$$
будем называть показательно-степенной и обозначать
$$
u(x)^.\nonumber
$$
Таким образом, по определению
$$
u(x)^=e^.\nonumber
$$
Если \(u,\;v\) — функции, непрерывные на \(\Delta\), то функция \(u^\) непрерывна на \(\Delta\) как суперпозиция непрерывных функций \(e^t\) и \(t=v(x)\ln\).

Источник