доказать что в треугольнике все углы острые
Остроугольный треугольник, элементы, свойства, признаки и формулы
Остроугольный треугольник, элементы, свойства, признаки и формулы.
Остроугольный треугольник – это треугольник, у которого все углы острые.
Остроугольный треугольник (понятие и определение):
Остроугольный треугольник – это треугольник, у которого все углы острые, т.е. меньше 90°.
Остроугольный треугольник – это треугольник, у которого все три угла острые. В свою очередь, острый угол – это угол, градусная мера которого составляет менее 90 градусов.
Рис. 1. Остроугольный треугольник
∠ АВС, ∠ BАC, ∠ BСA – острые углы треугольника
По определению, каждый правильный (равносторонний) треугольник также является остроугольным, но не каждый остроугольный треугольник – правильным (равносторонним). Иными словами, правильный (равносторонний) треугольник является частным случаем остроугольного треугольника. У равностороннего треугольника каждый угол составляет 60 °.
Рис. 2. Равносторонний треугольник
АВ = ВС = АС – стороны треугольника,
∠ АВС = ∠ BАC = ∠ BСA = 60° – углы треугольника
Рис. 3. Равнобедренный треугольник
АВ = ВС – боковые стороны, АС – основание,
∠ АВС – вершинный угол, ∠ BАC и ∠ BСA – углы при основании
Хотя в остроугольном треугольнике каждый угол меньше 90 градусов, сумма углов в треугольнике всегда равна 180 градусам.
Элементы остроугольного треугольника:
Рис. 4. Остроугольный треугольник и внешний угол
Медиана остроугольного треугольника (как и любого другого треугольника), соединяющая вершину треугольника с противоположной стороной, делит ее пополам, т.е. на два одинаковых отрезка.
Рис. 5. Остроугольный треугольник и медиана остроугольного треугольника
MС – медиана остроугольного треугольника
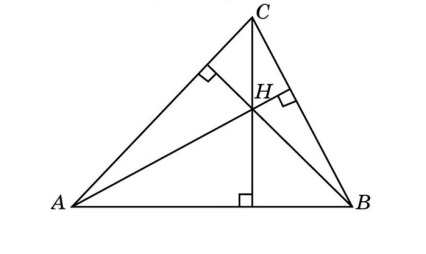
Все три медианы треугольника пересекаются в одной точке, которая называется центроидом или центром тяжести треугольника, и делятся этой точкой на две части в отношении 2:1, считая от вершины.
Рис. 6. Остроугольный треугольник и высота остроугольного треугольника
MС – высота остроугольного треугольника
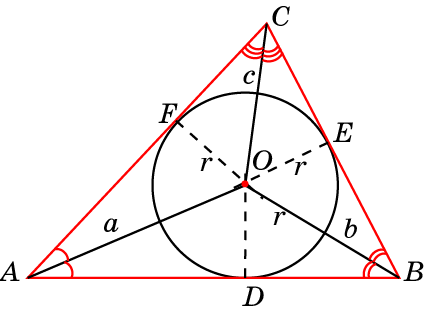
Высота остроугольного треугольника находится внутри треугольника. Все 3 высоты остроугольного треугольника (как и любого треугольника) пересекаются в одной точке, называемой ортоцентром.
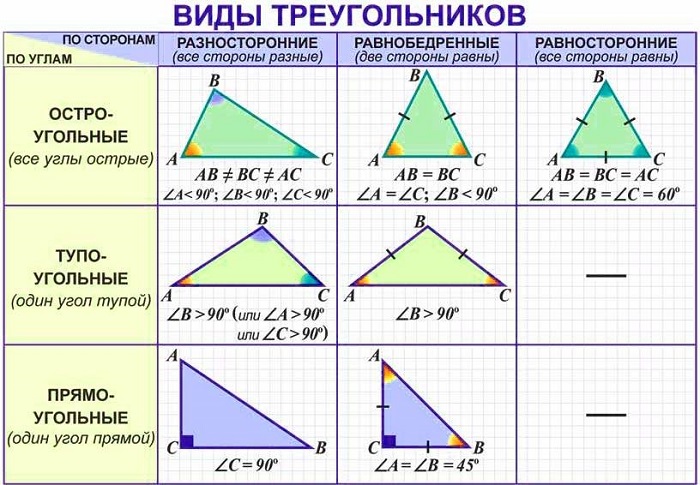
Биссектриса в остроугольном треугольнике (как и в любом другом треугольнике) делит угол пополам. Биссектрисы пересекаются в точке, которая является центром вписанной окружности.
Рис. 7. Остроугольный треугольник и биссектриса угла остроугольного треугольника
MС – биссектриса угла остроугольного треугольника
Кроме того, биссектриса остроугольного треугольника (как и любого другого треугольника) делит противолежащую сторону на отрезки, пропорциональные прилежащим сторонам треугольника
Свойства остроугольного треугольника:
Свойства остроугольного треугольника аналогичны свойствам обычного треугольника:
1. Против большей стороны лежит больший угол, и наоборот.
Рис. 8. Остроугольный треугольник
2. Против равных сторон лежат равные углы, и наоборот.
Рис. 9. Остроугольный треугольник с равными боковыми сторонами
3. Сумма углов остроугольного треугольника равна 180°.
4. Любая сторона остроугольного треугольника меньше суммы двух других сторон и больше их разности:
Докажите что в любом треугольнике либо все углы острые, либо два угла острые, а третий тупой или прямой?
Докажите что в любом треугольнике либо все углы острые, либо два угла острые, а третий тупой или прямой.
Сумма углов треугольника = 180 градусов.
Если один из углов прямой (90 градусов) на два остальных приходится тоже 90.
Какой из перечисленных треугольников существует?
Какой из перечисленных треугольников существует?
Тогда остальные углы будут
Какой треугольник называется тупоугольным?
Как называются стороны прямоугольного треугольника?
1)против большей стороны лежит большой угол ;
2)обратно, против большого угла лежит большая сторона.
Что такое неравенство треугольника?
Возможно ли в четырехугольникеа) два угла острые?
Возможно ли в четырехугольникеа) два угла острые?
? может ли быть у четырех угольника :1) три прямых угла и один острый?
? может ли быть у четырех угольника :
1) три прямых угла и один острый?
2) три прямых угла и один тупой?
3) четыре прямых угла?
4) четыре острых угла?
5) два прямых и два тупых угла?
6) два прямых угла, один острый и один тупой?
В тупоугольном треугольнике могут быть : 1) Прямой и острый углы 2) Тупой и прямой углы 3) Два тупых угла 4) Тупой и два острых угла?
В тупоугольном треугольнике могут быть : 1) Прямой и острый углы 2) Тупой и прямой углы 3) Два тупых угла 4) Тупой и два острых угла.
В остроугольном треугольнике : 1?
В остроугольном треугольнике : 1.
Один тупой угол, остальные острые 3.
Один прямой угол, остальные острые 4.
Менее трех острых углов.
В остроугольном треугольнике Все углы острые Один тупой угол, остальные острые Один прямой угол, остальные острые Менее трёх острых углов 3.
Внутренние углы треугольника пропорциональны числам 3, 5 и 7.
Чему равен на больший из его углов?
Одна из центральных тем на уроках геометрии – остроугольный треугольник, составная часть своих более сложных аналогов и иных тригонометрических форм.
Азы изучения точной науки начинаются с рассмотрения уникальной комбинации из трех сторон и острых углов.
Виды, признаки и свойства остроугольных треугольников
Трехсторонние фигуры разделяются на множество подвидов и категорий.
Общая классификация по наибольшему углу делит их на 3 группы:
Они располагают как общими для формы с тремя сторонами характеристиками, так и специфическими признаками.
3 угла, сумма которых равна 180°, (величина каждого меньше 90°) и 3 стороны;
сумма длин любых двух сторон больше оставшейся третьей.
Свойства остроугольной фигуры определяются вспомогательными геометрическими линиями, всегда находящимися внутри него:
1. Биссектрисы, делящие углы пополам, являются центром, вокруг которого можно нарисовать вписанную окружность.
2. Высоты пересекаются в одной точке, образуя ортоцентр.
3. Медианы в точке пересечения пролегают в пропорции 2:1 (2 трети до центра и 1 треть после).
Уникальные особенности зависят от разновидностей фигуры.
Равносторонний треугольник
Полное равенство придает и другую особенность: медианы, биссектрисы и высоты полностью совпадают.
Разносторонний треугольник
Наиболее часто встречаемый на чертежах в геометрии вариант, один из самых трудноразрешимых видов. Разносторонними бывают и прямоугольные, и тупоугольные фигуры.
Уникальных отличий не имеет, только общие:
все параметры имеют разные значения;
совпадений между вспомогательными линиями нет.
Равнобедренный остроугольный треугольник
Здесь при основании (стороне, не равной остальным) находятся равные друг другу 2 стороны и 2 угла. Выглядит как вытянутый в одну сторону равносторонний треугольник.
проведенная к основанию линия – и биссектриса, и высота, и медиана;
вспомогательные линии из крайних точек при основании совпадают.
Равнобедренный тупоугольный треугольник
Пусть он и называется равнобедренным, но из-за наличия угла более 90° не является остроугольным и является представителем другой группы.
Начертить его сложнее (рисунок следует начинать с основания и 2 острых углов и уже после создавать тупой), но процесс решения и изучения прост.
Отличие у него одно – точка пересечения двух высот, проведенных от углов при основании, выходит за периметр треугольника. Чтобы ее обозначить, необходимо нарисовать «продолжения» равнобедренных линий. Все остальные свойства совпадают.
В ключевых и фундаментальных разделах математики именно треугольник является основой для доказательства многих теорем и помощью в решении множества задач. Твердое знание его свойств откроет путь к успехам в расчетах, вычислениях, оформлении чертежей и фото в проектных работах.
§ 1. Сумма углов треугольника
Теорема о сумме углов треугольника
В этой главе мы снова обращаемся к треугольникам и будем обсуждать различные их свойства, при этом большое внимание уделим прямоугольным треугольникам, т. е. таким треугольникам, у которых один угол прямой. Некоторые свойства прямоугольных треугольников находят практическое применение, например, в конструкциях уголковых отражателей, которые широко используются в различных устройствах — от велосипедов до космических аппаратов. Об этом также будет рассказано в данной главе.
Докажем одну из важнейших теорем геометрии — теорему о сумме углов треугольника.
| Сумма углов треугольника равна 180°. |
Рассмотрим произвольный треугольник АВС и докажем, что
Проведём через вершину В прямую а, параллельную стороне АС (рис. 125, а). Углы 1 и 4 являются накрест лежащими углами при пересечении параллельных прямых а и АС секущей АВ, а углы 3 и 5 — накрест лежащими углами при пересечении тех же параллельных прямых секущей ВС. Поэтому
Очевидно, сумма углов 4, 2 и 5 равна развёрнутому углу с вершиной В, т. е. ∠4 + ∠2 + ∠5 = 180°. Отсюда, учитывая равенства (1), получаем: ∠1 + ∠2 + ∠3 = 180°, или ∠A + ∠B + ∠C = 180°. Теорема доказана.
Внешним углом треугольника называется угол, смежный с каким-нибудь углом этого треугольника. Докажем, что внешний угол треугольника равен сумме двух углов треугольника, не смежных с ним.
Обратимся к рисунку 125, б, на котором угол 4 — внешний угол, смежный с углом 3 данного треугольника. Так как ∠4 + ∠3 = 180°, а по теореме о сумме углов треугольника (∠1+ ∠2) + ∠3 = 180°, то ∠4 = ∠1 + ∠2, что и требовалось доказать.
Остроугольный, прямоугольный и тупоугольный треугольники
Из теоремы о сумме углов треугольника следует, что если в треугольнике один из углов прямой или тупой, то сумма двух других углов не превосходит 90°, и поэтому каждый из них острый. Таким образом, в любом треугольнике либо все углы острые, либо два угла острые, а третий тупой или прямой.
Если все три угла треугольника острые, то треугольник называется остроугольным (рис. 126, а). Если один из углов треугольника тупой, то треугольник называется тупоугольным (рис. 126, б). Если один из углов треугольника прямой, то треугольник называется прямоугольным. Сторона прямоугольного треугольника, лежащая против прямого угла, называется гипотенузой, а две другие стороны — катетами. На рисунке 126, в изображён прямоугольный треугольник АВС с прямым углом С.
Задачи
223. Найдите угол С треугольника АВС, если:
224. Найдите углы треугольника АВС, если ∠A : ∠B : ∠C = 2 : 3 : 4.
225. Докажите, что каждый угол равностороннего треугольника равен 60°.
226. Докажите, что углы при основании равнобедренного треугольника острые.
227. Найдите углы равнобедренного треугольника, если: а) угол при основании в два раза больше угла, противолежащего основанию; б) угол при основании в три раза меньше внешнего угла, смежного с ним.
228. Найдите углы равнобедренного треугольника, если один из его углов равен: а) 40°; б) 60°; в) 100°.
229. В равнобедренном треугольнике АВС с основанием АС проведена биссектриса AD. Найдите ∠ADC, если ∠C = 50°.
230. Биссектрисы углов А и В треугольника АВС пересекаются в точке М. Найдите ∠AMB, если ∠A = 58°, ∠B = 96°.
231. Медиана AM треугольника АВС равна половине стороны ВС. Докажите, что треугольник АВС прямоугольный.
232. Верно ли утверждение: если треугольник равнобедренный, то один из его внешних углов в два раза больше угла треугольника, не смежного с этим внешним углом?
233. Докажите, что биссектриса внешнего угла при вершине равнобедренного треугольника, противолежащей основанию, параллельна основанию.
234. Один из внешних углов равнобедренного треугольника равен 115°. Найдите углы треугольника.
235 В равнобедренном треугольнике АВС с основанием АС проведена биссектриса AD. Найдите углы этого треугольника, если ∠ADB = 110°.
Ответы к задачам
224. ∠A = 40°, ∠B = 60°, ∠C = 80°.
227. a) 36°, 72° и 72°; б) 45°, 45° и 90°.
228. a) 40°, 40° и 100° или 40°, 70° и 70°; б) 60°, 60° и 60°; в) 100°, 40° и 40°.
231. Указание. Воспользоваться свойством углов при основании равнобедренного треугольника.
233. Указание. Учесть, что внешний угол при вершине равнобедренного треугольника, противолежащей основанию, в два раза больше угла при основании.
234. 57°30′, 57°30′, 65° или 65°, 65°, 50°.
Геометрия. 7 класс
Конспект урока
Сумма углов треугольника
Перечень рассматриваемых вопросов:
Внешний угол треугольника– это угол, смежный с каким-либо углом этого треугольника.
Теоретический материал для самостоятельного изучения.
Ранее, на уроках математики, вы познакомились с различными геометрическими фигурами, в том числе и с треугольниками. При изучении геометрии, вы узнали признаки равенства треугольников, выяснили, что такое медиана, биссектриса и высота треугольника.
Сегодня мы продолжим изучать треугольники и рассмотрим одну из важнейших теорем геометрии– теорему о сумме углов треугольника.
Сформулируем эту теорему.
Сумма углов треугольника равна 180°.
Проведем через вершину В прямую а ║АС.
∠1 = ∠4 (по свойству параллельных прямых, т. к. это накрест лежащие углы при пересечении прямых а и АС и секущей АВ), ∠3 = ∠5 (по свойству параллельных прямых, т. к. это – накрест лежащие углы при пересечении прямых а и АС и секущей ВС)→ ∠4 + ∠2 + ∠5 = 180° (по свойству развёрнутого угла) → ∠1 + ∠2 + ∠3 = 180° → ∠А + ∠В + ∠С = 180°.
Что и требовалось доказать.
Теперь введём ещё одно понятие, связанное с треугольниками –внешний угол треугольника. Это угол, смежный с каким-либо углом этого треугольника.
Докажем, что внешний угол треугольника равен сумме двух углов треугольника, не смежных с ним.
∠3 + ∠4 = 180° (по свойству развёрнутого угла).
∠3 + (∠2 + ∠1) = 180° (по теореме о сумме углов треугольника) → ∠4 = ∠2 + ∠1.
Что и требовалось доказать.
Из теоремы о сумме углов треугольника следует, что если один из углов треугольника равен 90 градусам или больше 90 градусов, то остальные два угла будут острые, т.к. их сумма не должна превышать 90 градусов. Поэтому, в любом треугольнике либо все углы острые, либо два угла острые, а третий тупой или прямой.
Исходя из этого, можно классифицировать треугольники по углам.
По углам треугольник может быть:
‑ остроугольным, если все его углы являются острыми (т.е. меньше 90°);
‑ тупоугольным, если один из его углов тупой (т.е. больше 90°);
‑ прямоугольным, если один угол 90° (т.е. прямой).
В прямоугольном треугольнике стороны имеют свои названия.
Сторона треугольника, лежащая напротив прямого угла, называется гипотенузой, а две другие – катетами.
Докажем свойство прямоугольного треугольника, которое устанавливается с помощью теоремы о сумме углов треугольника.
Сумма двух острых углов прямоугольного треугольника равна 90º.
∠А +∠С + ∠В = 180° (по теореме о сумме углов треугольника).
∠В = 90° (по определению прямоугольного треугольника) →∠А + ∠С + 90° = 180°
Что и требовалось доказать.
Докажем, что в равностороннем треугольнике каждый угол равен 60 °.
Доказать: ∠А =∠С = ∠В = 60°.
Так как треугольник АВС равносторонний →АС = АВ = ВС (по определению равностороннего треугольника) → если АС = АВ → ∠С = ∠В (по свойству равнобедренного треугольника). Аналогично, если АС = СВ → ∠А = ∠В (по свойству равнобедренного треугольника) → ∠А = ∠С = ∠В.
∠А + ∠С + ∠В = 180° (по теореме о сумме углов треугольника).
∠А = ∠С = ∠В = 180° : 3 = 60°.
Что и требовалось доказать.
Материал для углублённого изучения темы.
Одно из свойств прямоугольного треугольника ‑сумма двух его острых углов равна 90°‑используется в технике, например, в угловом отражателе. Это устройство, которое отражает падающий на него пучок параллельных лучей при любом расположении отражателя по отношению к падающему пучку лучей.
Отражатель, например, устанавливается на заднем крыле велосипеда, для того, чтобы «возвращать назад» свет автомобильных фар, чтобы водитель машины видел велосипедиста ночью.
Ещё угловой отражаетель был установлен на автоматической космической станции, запущенной на Луну( выделен на рисунке кружочком), с целью определения точного расстояния от Земли до Луны.
Разбор заданий тренировочного модуля
1. Чему равна градусная мера углаА, если треугольник АВС прямоугольный?
По условию, ∆АВС – прямоугольный → сумма его острых углов равна 90°.
2. По рисунку найдите угол N треугольника FNA.
По рисунку ∠NAP= 140°, этот угол внешний к углу А треугольника FNA→
∠NAP = ∠N +∠F= 140° (т.к. внешний угол треугольника равен сумме двух углов треугольника не смежных с ним).