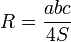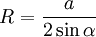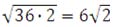докажите что около любого треугольника можно описать окружность притом единственную
Описанная окружность
Теорема
| Около любого треугольника можно описать окружность. |
Доказательство
Дано: произвольный 
АВС.
Доказать: около АВС можно описать окружность.
Доказательство:
1. Проведем серединные перпендикуляры к сторонам АВС, которые пересекутся в точке О (по свойству серединных перпендикуляров треугольника). Соединим точку О с точками А, В и С (Рис. 2).
Точка О равноудалена от вершин АВС (по теореме о серединном перпендикуляре), поэтому ОА = ОВ = ОС. Следовательно, окружность с центром О радиуса ОА проходит через все три вершины треугольника, значит, является описанной около АВС. Теорема доказана.
Замечание 1
| Около треугольника можно описать только одну окружность. |
Доказательство
Предположим, что около треугольника можно описать две окружности. Тогда центр каждой из них равноудален от его вершин и поэтому совпадает с точкой О пересечения серединных перпендикуляров к сторонам треугольника, а радиус равен расстоянию от точки О до вершин треугольника. Следовательно, эти окружности совпадают, т.е. около треугольника можно описать только одну окружность. Что и требовалось доказать.
Замечание 2
| Около четырехугольника не всегда можно описать окружность. |
Доказательство
Рассмотрим, например, ромб, не являющийся квадратом. Такой ромб можно «поместить» в окружность так, что две его вершины будут лежать на этой окружности (Рис. 3), но нельзя «поместить» ромб в окружность так, чтобы все его вершины лежали на окружности, т.к. диаметр окружности, равный одной из диагоналей ромба, будет больше (меньше) второй диагонали, т.е. нельзя описать окружность. Что и требовалось доказать.
Если же около четырехугольника можно описать окружность, то его углы обладают следующим замечательным свойством:
Доказательство
Рассмотрим четырехугольник АВСD, вписанный в окружность (Рис. 4).
Верно и обратное утверждение:
Доказательство
Доказать: около АВСD можно описать окружность.
Доказательство:
Предположим, что это не так. Тогда вершина С лежит либо внутри круга, либо вне его.
Рассмотрим первый случай, когда точка С лежит внутри круга (Рис. 6).
BАD — вписанный, тогда по теореме о вписанном угле BАD = 
ВЕD, тогда BАD + BСD
(ВЕD + ВАD).
Рассмотрим второй случай, когда точка С лежит вне круга (Рис. 7).
Подставим (3) и (4) в (2), получим:
Примечание:
Окружность всегда можно описать:
Поделись с друзьями в социальных сетях:
Окружность, описанная около треугольника.
Треугольник, вписанный в окружность. Теорема синусов
 Серединный перпендикуляр к отрезку |
| Окружность описанная около треугольника |
| Свойства описанной около треугольника окружности. Теорема синусов |
| Доказательства теорем о свойствах описанной около треугольника окружности |
Серединный перпендикуляр к отрезку
Таким образом, в случае, когда точки E и A лежат по разные стороны от серединного перпендикуляра, мы получили противоречие.
Полученное противоречие и завершает доказательство теоремы 2
Окружность, описанная около треугольника
Свойства описанной около треугольника окружности. Теорема синусов
| Фигура | Рисунок | Свойство | ||||
| Серединные перпендикуляры к сторонам треугольника |  | Все серединные перпендикуляры, проведённые к сторонам произвольного треугольника, пересекаются в одной точке. Посмотреть доказательство | ||||
| Окружность, описанная около треугольника |  | Около любого треугольника можно описать окружность. Центром описанной около треугольника окружности является точка, в которой пересекаются все серединные перпендикуляры, проведённые к сторонам треугольника. Посмотреть доказательство | ||||
| Центр описанной около остроугольного треугольника окружности | Центр описанной около остроугольного треугольника окружности лежит внутри треугольника. | |||||
| Центр описанной около прямоугольного треугольника окружности |  | Центром описанной около прямоугольного треугольника окружности является середина гипотенузы. Посмотреть доказательство | ||||
| Центр описанной около тупоугольного треугольника окружности |  | Центр описанной около тупоугольного треугольника окружности лежит вне треугольника. | ||||
| Теорема синусов |  |
| Серединные перпендикуляры к сторонам треугольника |
|
Все серединные перпендикуляры, проведённые к сторонам произвольного треугольника, пересекаются в одной точке.
Около любого треугольника можно описать окружность. Центром описанной около треугольника окружности является точка, в которой пересекаются все серединные перпендикуляры, проведённые к сторонам треугольника.
Центр описанной около остроугольного треугольника окружности лежит внутри треугольника.
Центром описанной около прямоугольного треугольника окружности является середина гипотенузы.
Центр описанной около тупоугольного треугольника окружности лежит вне треугольника.
Для любого треугольника справедливы равенства (теорема синусов):
,
Для любого треугольника справедливо равенство:
Для любого треугольника справедливо равенство:
Доказательства теорем о свойствах описанной около треугольника окружности
Следовательно, справедливо равенство:
откуда с помощью теоремы 2 заключаем, что точка O лежит на серединном перпендикуляре к отрезку BC. Таким образом, все три серединных перпендикуляра проходят через одну и ту же точку, что и требовалось доказать.
При доказательстве теоремы 3 было получено равенство:
.
Рассмотрим сначала случай, когда одна из сторон вписанного угла является диаметром окружности (рис.8).
Поскольку все вписанные углы, опирающиеся на одну и ту же дугу, равны, то для произвольного вписанного угла всегда найдется равный ему вписанный угол, у которого одна из сторон является диаметром окружности.
Формула (1) доказана.
Из формулы (1) для вписанного треугольника ABC получаем (рис.7):
Вокруг треугольника можно описать окружность
Окружность является описанной около треугольника, если все вершины треугольника лежат на этой окружности. Такой треугольник называется вписанным в окружность.
Существует теорема о том, что около каждого треугольника можно описать окружность, притом только одну. Докажем ее.
Пусть дан треугольник, к сторонам которого проведены срединные перпендикуляры. Как известно, срединные перпендикуляры треугольника всегда пересекаются в одной точке, и эта точка равноудалена от вершин треугольника. Значит, расстояние от точки пересечения срединных перпендикуляров до любой из вершин треугольника одно и то же, что может послужить радиусом одной окружности. И на этой окружности будут лежать вершины треугольника. Таким образом, она окажется описанной около него.
Чтобы убедиться в вышесказанном, рассмотрим рисунок:
Здесь дан треугольник ABC. К его сторонам проведены срединные перпендикуляры, которые пересекаются в точке O: OP ⊥ AB, OQ ⊥ BC, OR ⊥ CA.
Рассмотрим треугольники AOP и BOP. Они равны друг другу по двум равным сторонам и углу между ними: OP — общая сторона, углы при вершине P прямые, AP = BP по условию (т. к. OP срединный перпендикуляр, а значит делить AB пополам). Исходя из равенства этих треугольников, мы можем заключить, что AO = BO.
Если аналогично рассмотреть пары треугольников BOQ и COQ, COR и AOR, то можно прийти к выводу, что BO = CO, а CO = AO.
Следовательно, расстояния от точки пересечения срединных перпендикуляров треугольника до вершин этого треугольника одинаковы. Если представить, что это расстояние равно радиусу окружности с центром в точке O, то понятно, что вершины треугольника будут лежать на этой окружности.
Факт того, что около любого треугольника можно описать окружность, можно считать доказанным. Это следует из того, что к сторонам любого треугольника можно провести срединные перпендикуляры, которые всегда будут пересекаться в одной точке.
Теперь следует доказать, что описанная окружность может быть только одна. Если все вершины треугольника лежат на окружности, то это значит, что центр этой окружности находится на одинаковом расстоянии от каждой вершины треугольника. Но есть только одна точка, удаленная от вершин треугольника на одно и то же расстояние — это точка пересечения его срединных перпендикуляров. Таким образом нет других окружностей (с другими центрами и другими радиусами), которые были бы описаны вокруг треугольника.
Докажите что около любого треугольника можно описать окружность притом единственную
ТЕМА УРОКА: Окружность, описанная около треугольника.
Содержание
Цели урока:
Задачи урока:
План урока:
Введение.
Тема «Вписанные и описанные окружности в треугольниках» является одной из самых сложных в курсе геометрии. На уроках ей уделяется очень мало времени.
Геометрические задачи этой темы включаются во вторую часть экзаменационной работы ЕГЭ за курс средней школы.
Для успешного выполнения этих заданий необходимы твердые знания основных геометрических фактов и некоторый опыт в решении геометрических задач.
Теоретическая часть.
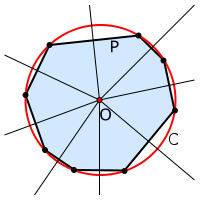
Описанная окружность многоугольника — окружность, содержащая все вершины многоугольника. Центром является точка (принято обозначать O) пересечения серединных перпендикуляров к сторонам многоугольника.
Центр описанной окружности выпуклого n-угольника лежит в точке пересечения серединных перпендикуляров к его сторонам. Как следствие: если рядом с n-угольником описана окружность, то все серединные перпендикуляры к его сторонам пересекаются в одной точке (центре окружности).
Вокруг любого правильного многоугольника можно описать окружность.
Для треугольника.
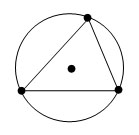
Окружность называется описанной около треугольника, если она проходит через все его вершины.
Вокруг любого треугольника можно описать окружность, притом только одну. Её центром будет являться точка пересечения серединных перпендикуляров.
У остроугольного треугольника центр описанной окружности лежит внутри, у тупоугольного — вне треугольника, у прямоугольного — на середине гипотенузы.
 |  |  |
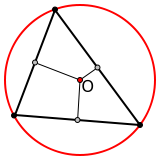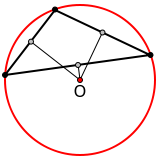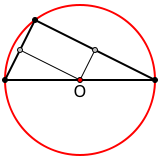| Остроугольный | Тупоугольный | Прямоугольный |
Радиус описанной окружности может быть найден по формулам:
Где:
a,b,c — стороны треугольника,
α — угол, лежащий против стороны a,
S — площадь треугольника.
Файл:T.gif Теорема. Теорема о центре окружности, описанной около треугольника.
Центр окружности, описанной около треугольника, является точкой пересечения перпендикуляров к сторонам треугольника, проведенных через середины этих сторон.
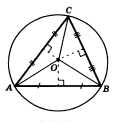
Пусть ABC – данный треугольник и O – центр окружности описанной около данного треугольника. Δ AOB – равнобедренный ( AO = OС как радиусы). Медиана OD этого треугольника одновременно является его высотой. Поэтому центр окружности лежит на прямой, перпендикулярной стороне AC и проходящей через ее середину. Так же доказывается, что центр окружности на перпендикулярах к другим сторонам треугольника.
Рассмотрим подробнее этот случай.
Дано:
Что и требовалось доказать.
Прямую, проходящую через середину отрезка перпендикулярно к нему, часто называют серединным перпендикуляром. В связи с этим иногда говорят, что центр окружности, описанной около треугольника, лежит на пересечении серединных перпендикуляров к сторонам треугольника.
Файл:T.gif Теорема. Теорема об окружности, описанной около треугольника. Около любого треугольника можно описать окружность.
АВС — данный треугольник; О — точка пересечения серединных перпендикуляров (рис. 31).
О — центр окружности, вписанной в АВС.
Обозначим буквой О точку пересечения серединных перпендикуляров к его сторонам и проведем отрезки ОА, ОВ и ОС. Так как точка О равноудалена от вершин треугольника АВС, то ОА=OB=ОС. Поэтому окружность с центром О радиуса ОА проходит через все три вершины треугольника и, значит, является описанной около треугольника ABC.
Отметим, что около треугольника можно описать только одну окружность. В самом деле, допустим, что около треугольника можно описать две окружности. Тогда центр каждой окружности равноудален от вершин треугольника и, значит, совпадает с точкой О пересечения серединных перпендикуляров к сторонам треугольника, а радиус равен расстоянию от точки О до вершин треугольника. Следовательно, эти окружности совпадают.
Практическая часть.
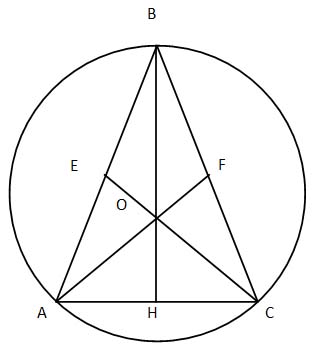
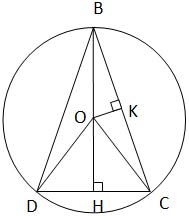
Около равнобедренного треугольника с основанием AC и углом при основании 75˚ описана окружность с центром O.
Найдите ее радиус, если площадь треугольника BOC равна 16.
∆ ABC – равнобедренный, AC – основание, ∠ ACB = 75˚,
площадь ∆ BOC равна 16
Найти:
Радиус описанной окружности
S = 1/2 ∙ BO ∙ OC ∙ sin ﮮ BOC (теорема о площади треугольника),
SBOC = 1/2 ∙ R ∙ R ∙ sin 150˚ = 1/2 ∙ R ∙ R ∙ 1/2 = 1/4 ∙ R 2 ;
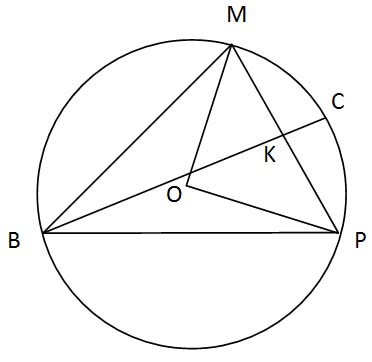
Треугольник BMP с углом B, равным 45˚, вписан в окружность радиуса 6.
Найдите длину медианы BK, если BK пересекает окружность в точке C и CK = 3.
Решение:
ﮮ MOP = 2 ﮮMBP
ﮮ MOP = 2 ∙ 45˚ = 90˚, следовательно, ∆ MOP – прямоугольный
MP 2 = OM 2 + OP 2
MP 2 = 62 + 62 = 36 + 36 = 36 ∙ 2
MP = 
MK = KP = 0,5 ∙ MP
MK = KP = 0,5 ∙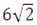 
= 
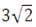
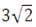
MK ∙ KP = BK ∙ KC∙ = BK ∙ 3
BK ∙ 3 = 9 ∙ 2
BK ∙ 3 = 18
BK = 6
Ответ: BK = 6
Остроугольный равнобедренный треугольник BCD с основанием CD, равным 16, вписан в окружность с центром O и радиусом 10. Найдите площадь треугольника BOC.
Интересный факт:
Софизм – это последовательность высказывания, рассуждений, построений, содержащая скрытую ошибку, за счет чего удается сделать неверный вывод. Задача обычно заключается в том, чтобы найти ошибку в рассуждениях.
Найдите ошибку в «доказательстве» того «странного» факта, что окружность имеет два центра.
Пусть даны две непараллельные прямые a и b. Из точек А и В этих прямых поставим перпендикуляры до пересечения в точке С. Через три точки А, В и С проведем окружность, пересекающую прямую а в точке М, а прямую b в точке N. По построению ∠MAC = ∠NBC = 900, значит, эти углы опираются на диаметры МС и NC построенной окружности. Середины этих диаметров – точки О1 и О2 – центры одной и той же окружности.
Ошибка в следующем:
∠MAC = ∠NBC = 900 (по построению). Эти углы являются вписанными и опирающимися на одну и туже дугу (в нашем случае, на полуокружность), поэтому точки О1 и О2 совпадают и лежат на отрезке DC (DC – биссектриса угла ADB).
Список использованных источников:
Поставить вопрос о современном образовании, выразить идею или решить назревшую проблему Вы можете на Образовательном форуме, где на международном уровне собирается образовательный совет свежей мысли и действия. Создав блог, Вы не только повысите свой статус, как компетентного преподавателя, а и сделаете весомый вклад в развитие школы будущего. Гильдия Лидеров Образования открывает двери для специалистов высшего ранга и приглашает к сотрудничеству в направлении создания лучших в мире школ.
- докажите что около любого прямоугольника можно описать окружность
- докажите что около четырехугольника можно описать окружность